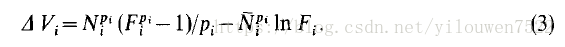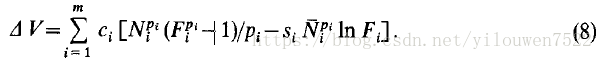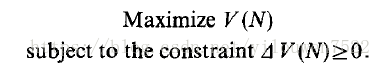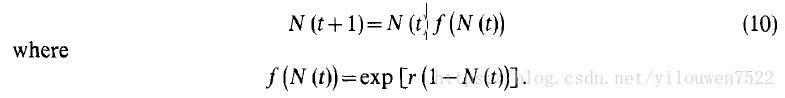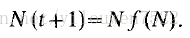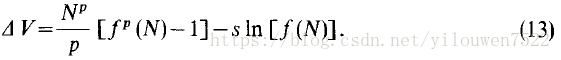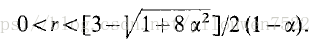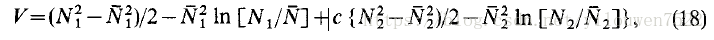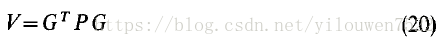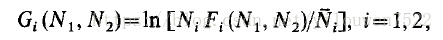一类相互作用种群离散时间模型的稳定性
概要
给出了一类相互作用种群离散时间模型的有效Lyapunov和类Lyapunov函数。 这些功能是建立在生物学上有意义的原则上的,即当其密度低时,可行的种群必须从外部来源吸收能量,并且当其密度高时必须将能量消耗到环境中。 这些函数可用于确定离散时间模型是全局稳定的,或者其解决方案最终局限于状态空间的可接受区域。 当模型具有混沌解决方案时,后者尤其有趣。 这些方法适用于单一物种模型和两个物种之间的竞争模型。
1.简介
人们越来越关注使用差分方程来模拟生态系统(Hassell和Comins,1976; Goh,1976; Innis,1974; May,1976; van der Vaart,1973)。 动态系统的差分方程表示也称为离散时间模型或系统。 对离散时间模型兴趣浓厚的一个原因是,当微分方程不能这样做时,它们可以提供生态系统的真实表示。
遗憾的是,非线性差分方程的理论非常有限,特别是与非线性微分方程理论相比较。 此外,即使是最简单的非线性差分方程也可能表现出非常复杂的行为范围(May,1976)。
离散时间模型的稳定性分析的标准方法检查在平衡处计算的某个矩阵的特征值。 但是这种方法只能保证相对于初始状态从平衡的小扰动的稳定性。 对小干扰的这种限制意味着分析可能没有实际意义。 另一种方法是在计算机上模拟一些解决方案。 对于具有三个以上状态变量的系统,这可能导致无意义输出的崩坏。
如果离散时间模型代表一个可行的生态系统,它必须相对于来自平衡的初始状态的有限干扰是稳定的,或者它必须具有在状态空间的可接受区域中开始的解将保持在相同区域中的性质, 没有进一步的干扰。确定离散时间模型全局稳定的一种方法是通过合适的Lyapunov函数。 通常,构建良好的Lyapunov函数需要相当大的独创性。 幸运的是,对于一类模型生态系统,我们可以通过具有生物学意义的原理构建有效的Lyapunov函数。 这个原则(Goh,1977a)指出,在可行的人口中,能量必须由高密度的人群消散,并且必须以低密度从周围的源吸收。
2.一般分析
在时间t,让Ni为涉及m种的相互作用中的第i种物质的密度。 假设可以通过以下方式描述交互
这种模型可用于描述竞争,共生,某些类型的猎物 - 捕食者相互作用或这种相互作用的复合体。
假设(1)在
Vi在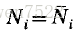
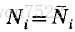



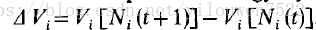
在可行的单一物种种群中,当








设cl,c2 ....,c m为正常数。 Lyapunov函数的良好候选者是
根据定义,
通常针对整个状态空间陈述离散时间模型的全局稳定性的条件。 在生态学中,全球稳定性的概念必须局限于每个物种密度为正的可行区域。 通过改造
通常针对整个状态空间陈述离散时间模型的全局稳定性的条件。 在生态学中,全球稳定性的概念必须局限于每个物种密度为正的可行区域。 通过改造
可以将可行区域映射到维度m的整个状态空间。 我们不会使用这种转变。 相反,我们稍微修改了标准Lyapunov定理的全局稳定性(Kalman和Bertram,1960)。
定理1:如果(5)的

使用该定理的一种方法是最大化可行区域中所有(N1,N 2 ......,Nm)的函数


假设模型(1)不是全局稳定的。 让它在


该函数的全局最小值为
与(5)相比,我们有一组额外的正参数s1,s2 ..... sm,它们可用于在尽可能大的区域中使

设Y为
然后可以使用可靠的约束优化程序,例如由Fletcher(Harwell子程序VF01A,Fletcher,1975)引起的罚函数方法。用V0表示该优化问题中V的最优值。由此得出所有





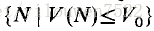




定理2:对于模型(1),令





3.单种群模型的稳定性和有界性
我们首先将第2节中概述的方法应用于简单的非线性差分方程
该等式可以被认为是一种库存补充模型,其中补充密度仅取决于前一代库存的密度。 参数r和K分别称为内在生长速率和承载能力。 模型(9)具有一系列有趣的行为,取决于参数r的值(May,1974,1975和1976)。 对于0 <r <2,该模型在n(t)= K时具有稳定的平衡点。对于2 <r <2.692,存在稳定的极限循环,并且对于r> 2.692,该模型具有混沌解。
设N(t)= n(t)/ K为人口密度。 然后可以将等式(9)表示为
为方便起见,我们今后将使用N来表示N(t)。 为了区分N(t + 1)和N(t),我们将继续保留其论点。 用这个约定公式(10)读
可以根据等式(2)中描述的类型的函数来检查等式(10)的全局稳定性。 让
V是一个合适的Lyapunov函数,因为对于0 <r <2,我们对所有N> 0和

对于满足2 <r <2.692的r的值,等式(10)具有阶段2“(1976年5月)的稳定极限环。考虑等式(7)的一维模拟,即。
其中p和s是正常数。 V则是“Lyapunov-like”函数,
我们的目的是使用定理2来证明在2 <r <2.692的情况下模型(10)存在最终约束区域Z. 对于p和s的给定值估计Z的策略基本上在第2节中概述,除了在单种情况下,Vo将出现在Y中的N的最小值或最大值。所获得的区域的大小将是 当然取决于所选择的p和s的值。 在一种情况下,对计算机进行编程以搜索选定的p和s值以获得Z的最佳值是一件简单的事情。
该方法用于r = 2.3,其对应于2点极限环,其中极限点在N = 0.408和N = 1.592。 在这种情况下,发现p = 3.69和s = 1.1给出了Z的合理估计。如式(12)和(13)所描述的函数V和
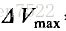

图1. CD是具有两点极限环的单一物种模型的最终限制区域
当r> 2.692时,等式(10)具有混沌解。 然而,仍然可以使用与稳定极限循环情况相同的方法来证明解决方案最终受到限制。 我们用r = 3.3来说明这一点。 图2显示了对于p = 1.51和s = 0.52,针对In(N)绘制的V和


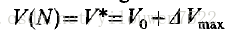
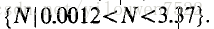
图2. CD是具有混沌解的单物种模型的最终限制区域
4.两种群模型的稳定性和有界性
考虑以下两种物种之间竞争的差异方程模型
这些方程的一个更简单的形式是当
在这种情况下,两个种群的承载能力相同,第二种种群的生长速度是第一种种群的两倍。 应当注意,对于比在等式(15)中指定的更宽范围的参数值,重复下面的分析。 选择的特殊情况(参见1974年5月的说明图)纯粹仅用于说明目的。
如果我们将
该系统的平衡点是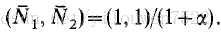
May(1974)已经表明,等式(16)的解表现出与单物种模型类似的行为类型。 为了使两个物种共存,我们需要0 <〜<1,并且稳定平衡点的标准是
对于
其中c是正常数。 然后
对于某些c值,很容易证明
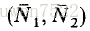

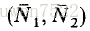
对于某些c值,很容易证明
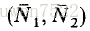

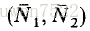






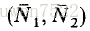
图3.具有全局稳定平衡的两种竞争中的
测试了其他类型的Lyapunov函数,发现它们适用于证明全局稳定性。 其中之一是
其中P是正定,对称矩阵,矢量G的分量是...
用式(17)描述的

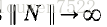






对于满足

对应于等式(8)我们有
我们的目的是选择常数P1,Pz,sl,s2和c2,以便获得最终约束区域Z的合理估计。显然,Z必须包含极限环。
对于给定的常数p1,p2,s1,s2和c2的值确定Z的过程在第2节中概述,并且对于r = 1.5和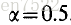
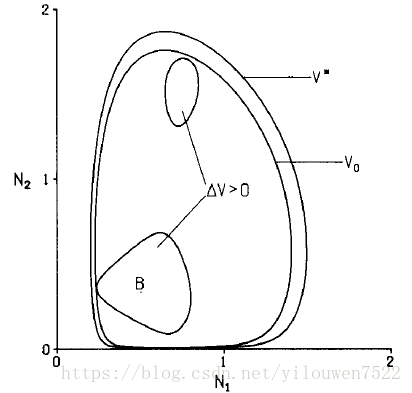
图4. V = V *定义了具有两点极限环的两种竞争的最终限制区域的边界
当然很可能存在与方程(21)不同形式的类Lyapunov函数,这导致对该模型的Z区域的较小估计。 尽管事实上我们希望这个程序能够在最终限制区域产生保守的结果。 测试了其他Lyapunov样函数,发现它们给出与方程(21)相似或更差的结果。 例如,对于各种矩阵P测试由等式(20)定义的函数。在r = 1.5,e = 0.5的情况下,P的条目受到以下要求的严格限制:
发现P~I = 1,P~2 = -0.39和P21 = 0.2的选择使得Z区域的尺寸与通过等式(21)给出的尺寸相当。
前面的部分使用了两个定理。 一个定理给出了离散时间模型在可行区域中全局稳定的充分条件。 另一个定理给出了离散时间模型的解最终被限制在状态空间的区域中的充分条件。 这似乎是第一次计算最终约束区域的定理已经制定并成功应用于离散时间模型。 离散模型的这个定理不是连续时间系统中最终约束定理的直接转换(Aggarwal,1972)。 由于离散时间模型的解不是状态空间中的连续路径,因此必须使用其他参数。
Lyapunov函数或Lyapunov函数的使用提供了比模拟研究更多的信息。 由于V和
参考
[1] Aggarwal,J。K。:关于非线性系统的注释。纽约:Van Nostrand Reinhold Co. 1972。
[2] Beddington,J.R.,Free,C.A.,Lawton,J。H。:捕食者 - 食饵模型中的动态复杂性以差分方程框架。 Nature 255,58--60(1975)。
[3] Fletcher,R。:约束优化的理想罚函数。 J. Inst。数学。 App 1~,319 - 342(1975)。
[4] Goh,B。S。:捕捞季节有限的渔业的最佳尺寸限制。 ECOL。建模(in press,1976)。
[5] Goh,B。S.:许多物种系统的全球稳定性。阿米尔。 NATUR。 (印刷中,1977a)。
[6] Goh,B。S.:在一个被剥削的渔业的库存招募模型中的稳定性。数学。 Biosc。 (在按,1977b)。
[7] Hassell,M。P.,Comins,H。N.:两种物种竞争的离散时间模型。理论值。流行。生物学。 9,202--221(1976)。
[8] Innis,G .:“软科学”研究中的动力学分析:在差分方程的辩护中,在:生物学中的数学问题(van den Driessche,P.,ed。),Biomath的讲义,卷。 2,pp.102--122。柏林 - 海德堡 - 纽约:施普林格1974年。
[9] Kalman,R。E.,Bertram,J。E.:通过“第二方法”进行控制系统分析和设计Lyapunov。 II离散时间系统。跨。 ASME D 82,394 --- 399(1960)。
[10] May,R.M。:不重叠世代的生物种群:稳定点,稳定周期和混乱。 Science 186,645--647(1974)。
[11] 5月,R。M.:遵守差分方程的生物种群:稳定点,稳定周期,
和混乱。 J. Theor。生物学。 51,511--524(1975)。
[12] May,R.M。:具有非常复杂动力学的简单数学模型。自然261,459467(1976)。
[13] Odum,E。P。:生态学基础,第3版。费城:W. B.桑德斯1971年。
[14] Van der Vaart,H。R。:对某些差分方程和相关方程的比较研究微分方程:对模型构建的影响。公牛。数学。生物学。 35,195--211(1973)。