最近在看高斯混合模型(Gaussian Mixture Model, GMM),涉及到高斯分布的参数。为此特意回顾了概率论的二维高斯分布的相关概念,并分析了参数对二维高斯分布曲面的影响。
1、多维高斯分布的概率密度函数
多维变量
的联合概率密度函数为:
其中:
d:变量维度。对于二维高斯分布,有d=2;
:各位变量的均值;
:协方差矩阵,描述各维变量之间的相关度。对于二维高斯分布,有:
后文主要分析均值和协方差矩阵对二维高斯分布的影响。
2、均值和协方差矩阵对二维高斯分布的影响
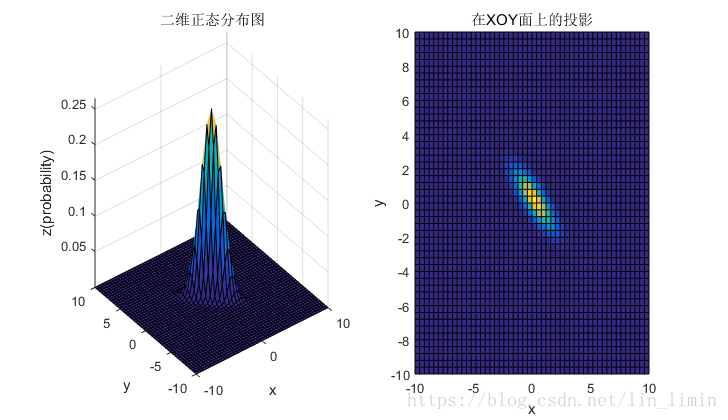
2.1
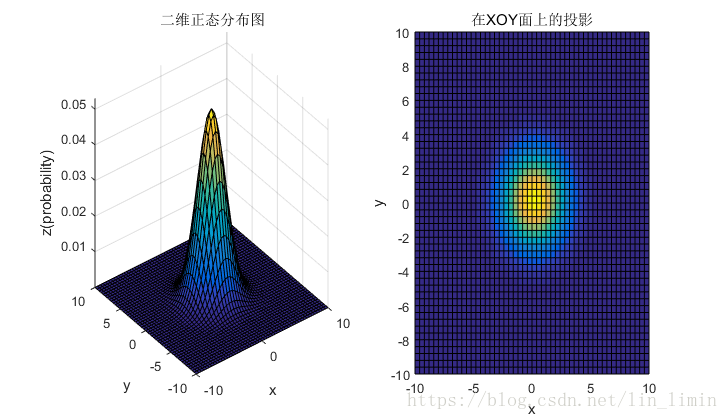
2.2
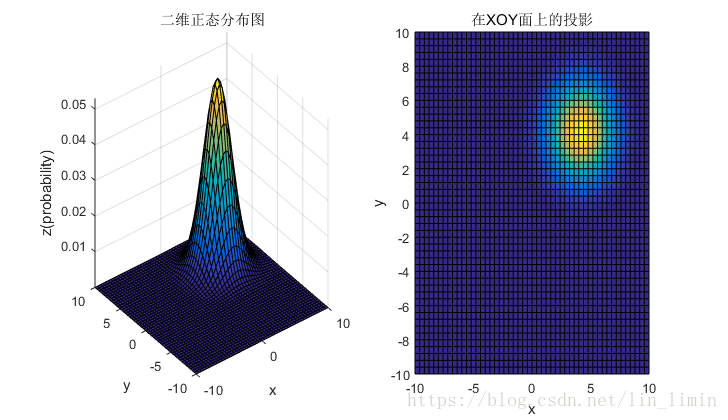
2.3
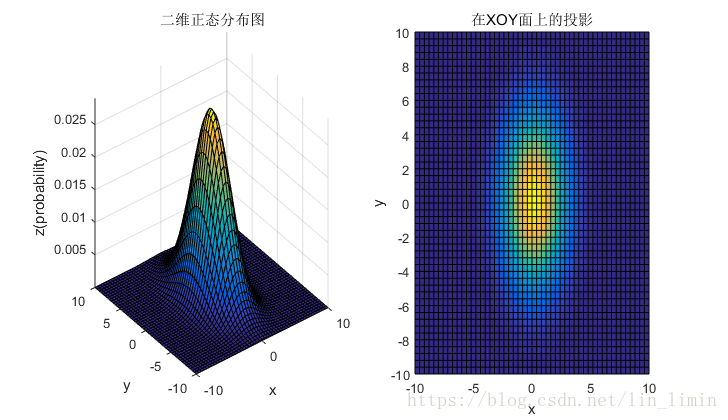
2.4
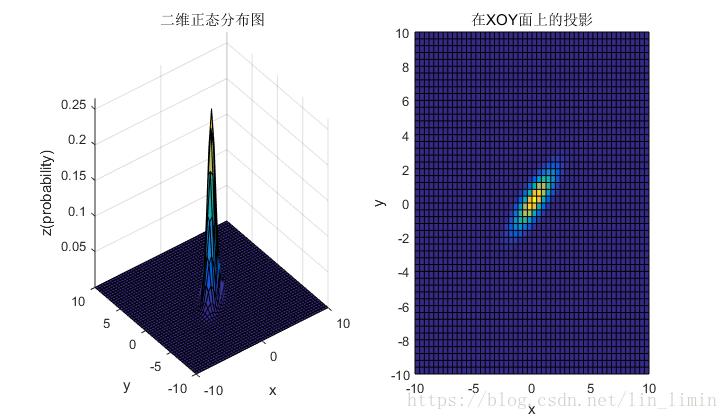
2.5
3、总结
①均值表征的是各维变量的中心,其对二维高斯曲面的影响较好理解,它使得整个二维高斯曲面在xoy平面上移动;
②对于协方差矩阵,对角线上的两个元素,即
和
表征的是x维和y维变量的方差,决定了整个高斯曲面在某一维度上的“跨度”,方差越大,“跨度”越大;
③协方差矩阵的斜对角线上面的两个元素,即
和
(
=
)表征的是各维变量之间的相关性:
>0说明x与y呈正相关(x越大,y越大),其值越大,正相关程度越大;
<0呈负相关;否则不相关。