动态规划--树形DP
1、什么是树型动态规划
顾名思义，树型动态规划就是在“树”的数据结构上的动态规划，平时作的动态规划都是线性的或者是建立在图上的，线性的动态规划有二种方向既向前和向后，相应的线性的动态规划有二种方法既顺推与逆推，而树型动态规划是建立在树上的，所以也相应的有二个方向：
1、叶－>根：在回溯的时候从叶子节点往上更新信息
2、根 - >叶：往往是在从叶往根dfs一遍之后（相当于预处理），再重新往下获取最后的答案。
不管是从 叶－>根 还是从 根 - >叶，两者都是根据需要采用，没有好坏高低之分。
1、叶－>根：在回溯的时候从叶子节点往上更新信息
2、根 - >叶：往往是在从叶往根dfs一遍之后（相当于预处理），再重新往下获取最后的答案。
不管是从 叶－>根 还是从 根 - >叶，两者都是根据需要采用，没有好坏高低之分。
2、树形动态规划的优美之处
树真的是一种特别特别优美的结构！用来做动态规划也简直是锦上添花再美不过的事，因为树本身至少就有“子结构”性质（树和子树）；也本身就具有递归性。所以在树上DP其实是其所当然的事，相比线性动态规划来讲，转移方程更直观，更易理解。
树真的是一种特别特别优美的结构！用来做动态规划也简直是锦上添花再美不过的事，因为树本身至少就有“子结构”性质（树和子树）；也本身就具有递归性。所以在树上DP其实是其所当然的事，相比线性动态规划来讲，转移方程更直观，更易理解。
3、难点
- 和线性动态规划相比，树形DP往往是要利用递归的，所以对递归不熟悉的同学，是一道小小的障碍，说是小小的，因为要去理解也不难.
- 细节多，较为复杂的树形DP，从子树，从父亲，从兄弟…已经一些小的要处理的地方，脑子不清晰的时候做起来颇为恶心
- 状态表示和转移方程，也是真正难的地方。做到后面，树形DP的老套路都也就那么多，难的还是怎么能想出转移方程，状压DP、概率DP这些特别的DP应该说做到最后都是这样！
通过dfs维护从根到叶子或从叶子到根的状态转移
********************************************************************************************************************
1. hdu 4123 Bob's Race 树形dp+RMQ
2.
hdu 4514 求树的直径+并查集判环
4.
hdu 4714 Tree2Cycle 思维
5.
hdu 3660 Alice and Bob's Trip 有点像对抗搜索
6.
hdu 2196 Computer 搜两遍
**************************************************************************************************************
1. hdu 4123 Bob's Race 树形dp+RMQ
题目大意：
给一棵树，n个节点，每条边有个权值，从每个点i出发有个不经过自己走过的点的最远距离Ma[i],有m个询问，每个询问有个q,求最大的连续节点区间长度ans，使得该区间内最大的M[i]和最小的M[j]之差不超过q。
解题思路：
树形dp+RMQ，几个基本的知识点杂糅在一起。
首先用树形dp求出从任意一点i出发的Ma[i].两遍dfs,第一遍求出每个节点为根到儿子方向的最大距离并记录最大距离得到的直接儿子，和与最大距离路径没有重边的次大距离。第二遍求出每个点的最远距离Ma[i]要么从儿子方向得到，要么从父亲方向得到。
把无根树转化成有根树分析：
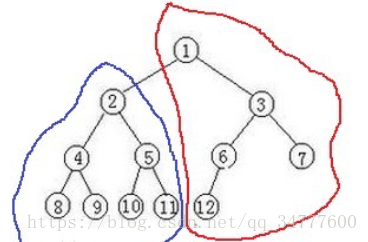
对于上面那棵树，要求距结点2的最长距离，那么，就需要知道以2为顶点的子树（蓝色圈起的部分，我们叫它Tree（2）），距顶点2的最远距离L1
还有知道2的父节点1为根节点的树Tree（1）-Tree(2)部分（即红色圈起部分），距离结点1的最长距离+dist(1,2) = L2，那么最终距离结点2最远的距离就是max{L1，L2}
f[i][0],表示顶点为i的子树的，距顶点i的最长距离
f[i][1],表示顶点为i的子树的，距顶点i的次长距离
f[i][2],表示Tree(i的父节点)-Tree(i)的最长距离+i跟i的父节点距离
要求所有的f[i][0]和f[i][1]很简单，只要先做一次dfs求每个结点到叶子结点的最长距离即可。
然后要求f[i][2], 可以从父节点递推到子节点，
假设节点u有n个子节点，分别是v1,v2...vn
那么
如果vi不是u最长距离经过的节点：
f[vi][2] = dist(vi,u)+max(f[u][0], f[u][2])
如果vi是u最长距离经过的节点，那么不能选择f[u][0],因为这保存的就是最长距离，要选择Tree（u）第二大距离f[u][1],
可得：
f[vi][2] = dist(vi, u) + max(f[u][1], f[u][2])
然后
求出Ma[i]数组后，可以用RMQ nlogn的时间复杂度来预处理所有区间的最大值和最小值。
然后对于每个询问q,用两个指针l,r.从前至后按以i开始能够达到最大的区间长度的顺序扫，不过当以i开始的最大的满足的区间长度为L时，向右移动l指针，此时r指针不必移动，因为现在只用考虑区间长度>=L的情况，这样就利用了只找可能满足的区间长度越来越大的情况的性质。这样每个位置最多进出一次，时间复杂度为o(N)。
所以总的时间复杂度为nlogn+m*n.
RMQ算法：是一个快速求区间最值的离线算法，预处理时间复杂度O（n*log(n)），查询O(1)，所以是一个很快速的算法，当然这个问题用线段树同样能够解决。
问题：给出n个数ai，让你快速查询某个区间的的最值。
算法分类：DP+位运算
算法分析：这个算法就是基于DP和位运算符，我们用dp【i】【j】表示从第 i 位开始，到第 i + 2^j -1 位的最大值或者最小值。
那么我求dp【i】【j】的时候可以把它分成两部分，第一部分从 i 到 i + 2 ^( j-1 ) - 1 ，第二部分从 i + 2 ^( j-1 ) 到 i + 2^j - 1 次方，其实我们知道二进制数后一个是前一个的二倍，那么可以把 i --- i + 2^j 这个区间 通过2^(j-1) 分成相等的两部分， 那么转移方程很容易就写出来了。
转移方程： mm [ i ] [ j ] = max ( mm [ i ] [ j - 1 ] , mm [ i + ( 1 << ( j - 1 ) ) ] [ j - 1 ] );
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include <algorithm>
#include <cstdio>
#include<cmath>
#include <cstring>
using namespace std;
#define inf 0x3f3f3f3f
#define maxn 50010
int dist[maxn][3];
int f[maxn];
int longest[maxn];
int head[maxn];
int n, m, id, q;
struct edge
{
int to;
int w;
int next;
}edges[2*maxn];
void add_edge(int u, int v, int w)
{
edges[id].to = v;
edges[id].w = w;
edges[id].next = head[u];
head[u] = id++;
}
int dfs1(int u, int fa)
{
if (dist[u][0] != -1) return dist[u][0];
dist[u][0] = dist[u][1] = dist[u][2] = 0;
for (int e = head[u]; e != -1; e = edges[e].next)
{
int v = edges[e].to;
if (v == fa) continue;
int dfs1_vu = dfs1(v, u);
if (dist[u][0] < dfs1_vu + edges[e].w)
{
dist[u][1] = dist[u][0];
longest[u] = v;
dist[u][0] = dfs1_vu + edges[e].w;
}
else if (dist[u][1] < dfs1_vu + edges[e].w)
{
dist[u][1] = dfs1_vu + edges[e].w;
}
}
return dist[u][0];
}
void dfs2(int u, int fa)
{
for (int e = head[u]; e != -1; e = edges[e].next)
{
int v = edges[e].to;
if (v == fa) continue;
if (longest[u] == v)
{
dist[v][2] = max(dist[u][2], dist[u][1]) + edges[e].w;
}
else
{
dist[v][2] = max(dist[u][2], dist[u][0]) + edges[e].w;
}
//cout << dist[1][2] << endl;
dfs2(v, u);
}
}
int dpmax[maxn][20];
int dpmin[maxn][20];
void initRMQ(int n, int d[])
{
for (int i = 1; i <= n; i++)
{
dpmax[i][0] = d[i];
dpmin[i][0] = d[i];
}
for (int j = 1; (1 << j) <= n; j++)
{
for (int i = 1; i + (1 << j) - 1 <= n; i++)
{
dpmax[i][j] = max(dpmax[i][j - 1], dpmax[i + (1 << (j - 1))][j - 1]);
dpmin[i][j] = min(dpmin[i][j - 1], dpmin[i + (1 << (j - 1))][j - 1]);
}
}
}
int rmq(int l, int r)
{
int k = 0;
while ((1 << (k + 1)) <= r - l + 1) k++;
return max(dpmax[l][k], dpmax[r - (1 << k)+1][k]) - min(dpmin[l][k], dpmin[r - (1 << k) + 1][k]);
}
int main()
{
while (cin >> n >> m&&n + m)
{
memset(head, -1, sizeof(head));
memset(dist, -1, sizeof(dist));
int u, v, w;
id = 0;
for (int i = 0; i < n - 1; i++)
{
cin >> u >> v >> w;
add_edge(u, v, w);
add_edge(v, u, w);
}
dfs1(1, -1);
dfs2(1, -1);
for (int i = 1; i <= n; i++)
f[i] = max(dist[i][0], dist[i][2]);
initRMQ(n, f);
while (m--)
{
cin >> q;
int l = 1, ans = 0;
for(int i = 1; i <= n; i++)
{
while (l<i&&rmq(l, i)>q) l++;
ans = max(ans, i - l + 1);
}
cout << ans << endl;
}
}
return 0;
}
*************************************************************************************************************
2. hdu 4514 求树的直径+并查集判环
题意：给定一个无向图，图可能是非连通的，如果图中存在环，就输出YES，否则就输出图中最长链的长度。
分析：首先我们得考虑这是一个无向图，而且有可能是非连通的，那么就不能直接像求树那样来求最长链。对于本题，首先得判断环，在这里我们就用并查集判环，因为并查集本身就是树型结构，如果要连接的两点的祖先都相同，那么就已经有环了，这样直接输出YES
若无环：无环，所以每个集合都是一个tree么，那么是tree就好办多了。dfs。
则： dis_max=max(dis_max,max(deep,dis[son_tree1]+dis[son_tree2]))。
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include <algorithm>
#include <cstdio>
#include<cmath>
#include <cstring>
using namespace std;
#define inf 0x3f3f3f3f
#define maxn 100010
int head[maxn];
int pre[maxn];
bool vis[maxn];
int dis_max;
int n, m, id;
struct edge
{
int to;
int w;
int next;
}edges[20*maxn];
void add_edge(int u, int v, int w)
{
edges[id].to = v;
edges[id].w = w;
edges[id].next = head[u];
head[u] = id++;
}
int find(int x)
{
int r = x;
while (r != pre[r]) r = pre[r];
//路径压缩
int i = x, j;
while (i != r)
{
j = pre[i];
pre[i] = r;
i = j;
}
return r;
}
void Union(int u, int v)
{
int x = find(u), y = find(v);
if (x != y)
{
pre[y] = x;
}
}
int dfs(int u, int deep, int w)
{
if (head[u] == -1) return 0;
vis[u] = 1;
int dis[2] = {0,0}, cnt = 0, maxr = 0, tmp, v;
for (int e = head[u]; e != -1; e = edges[e].next)
{
v = edges[e].to;
if (vis[v]) continue;
tmp = dfs(v, deep + edges[e].w, edges[e].w);
if (maxr < tmp) maxr = tmp;
if (cnt < 2) dis[cnt++] = tmp;
else
{
int f = (dis[0] < dis[1]) ? 0 : 1;
if (dis[f] < tmp) dis[f] = tmp;
}
}
if (dis_max < dis[0] + dis[1]) dis_max = dis[0] + dis[1];
return maxr + w;
}
int main()
{
int u, v, w;
bool non;
while (scanf("%d%d", &n, &m) != EOF)
{
id = 0; non = false;
memset(head, -1, sizeof(head));
memset(vis, 0, sizeof(vis));
for (int i = 1; i <= n; i++) pre[i] = i;
for (int i = 1; i <= m; i++)
{
scanf("%d%d%d", &u, &v, &w);
add_edge(u, v, w);
add_edge(v, u, w);
if (find(u) == find(v)) non = true; //注意：要保证两点之前并未加边
Union(u, v);
}
if (non) cout << "YES" << endl;
else
{
dis_max = 0;
for (int i = 1; i <= n; i++)
{
if (!vis[i]) dfs(i, 0, 0);
}
cout << dis_max << endl;
}
}
return 0;
}
*************************************************************************************************************
3. hdu 4126 Genghis Kehan the Conqueror Prim+树形dp 比较经典
题意：
一个N个点的无向图，先生成一棵最小生成树，然后给你Q次询问，每次询问都是x,y,z的形式， 表示的意思是在原图中将x,y之间的边增大(一定是变大的)到z时，此时最小生成数的值是多少。最后求Q次询问最小生成树的平均值。 N<=3000 , Q<=10000
思路：
先求出该图的最小生成树，用prim()， O(n^2)。
对于每次询问， 都是将a，b之间的边增加到c， 会出现 两种情况：
1. 如果边权增加的那条边原先就不在最小生成树中，那么这时候的最小生成树的值不变
2. 如果在原最小生成树中，那么这时候将增加的边从原最小生成树中去掉，这时候生成树就被分成了两个各自联通的部分，可以证明的是，这时候的最小生成树一定是将这两部分联通起来的最小的那条边。
问题转化：
首先我们先求出最小生成树，然后将在最小生成树中边去掉，对于每条最小生成树中的边，我们要求出它的替代边， 并且要求该替代边最小。
对于询问Q（10000） 分析一下Q里面的复杂度必须是O(n) 或 O(1)。
我们需要在外面预处理求出一些跟能推出答案但推出过程的复杂度是以上2个的其中1个。
假设两个各自连通的部分分别为树A，树B
1. 用
dp[i][j]表示树A中的点i 到 树B（j点所在的树）的最近距离，这个过程可以在一边dfs就可以出来，对于每个 i 的dfs 复杂度是O(n) ，外加一个n的循环求出每个点，这里的总复杂度为 O(n^2)。
2. 通过求出来的dp[i][j] 再用一个dfs
求出 树B 到 树A的最近距离，（方法：枚举树A中的所有点 到 树B的最近距离，取其中的最小值。）显然， 这个求出来的值是我们要的最小替代边，把它保存到一个best[i][j]数组里面，（best[i][j]表示去掉边<i，j>后它的最小替代边的值）这里的总复杂度为 O(n^2)。
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cmath>
#include<vector>
#include<cstring>
using namespace std;
#define inf 0x3f3f3f3f
#define maxn 3010
int map[maxn][maxn];
int dp[maxn][maxn];
int dis[maxn];
int pre[maxn];
bool vis[maxn];
int best[maxn][maxn];
vector<int> edges[maxn];
int n, m, q;
long long dis_max;
void init()
{
memset(map, inf, sizeof(map));
memset(dis, inf, sizeof(dis));
memset(dp, inf, sizeof(dp));
memset(pre, -1, sizeof(pre));
memset(vis, 0, sizeof(vis));
for (int i = 0; i < n; i++) edges[i].clear();
}
void prim()
{
int i, j, k;
for (i = 1; i < n; i++)
{
dis[i] = map[0][i];
pre[i] = 0;
}
dis[0] = inf;
vis[0] = 1;
pre[0] = -1;
dis_max = 0;
for (i = 0; i < n - 1; i++)
{
k = 0;
for (j = 1; j < n; j++)
{
if (!vis[j] && dis[k] > dis[j])
k = j;
}
vis[k] = 1;
dis_max += dis[k];
if (pre[k] != -1)
{
edges[k].push_back(pre[k]);
edges[pre[k]].push_back(k);
}
for (j = 1; j < n; j++)
{
if (!vis[j] && dis[j] > map[k][j])
{
dis[j] = map[k][j];
pre[j] = k;
}
}
}
}
int dfs1(int u, int fa, int rt) //rt到u及其子树的最小距离
{
int i;
for (i = 0; i < edges[u].size(); i++)
{
int v = edges[u][i];
if (v == fa) continue;
dp[rt][u] = min(dp[rt][u], dfs1(v, u, rt));
}
if (fa != rt) dp[rt][u] = min(dp[rt][u], map[rt][u]);
return dp[rt][u];
}
int dfs2(int u, int fa, int rt) //以rt为根及子树 到 以u为根及子树的最小距离
{
int i;
int ans = dp[u][rt];
for (i = 0; i < edges[u].size(); i++)
{
int v = edges[u][i];
if (v == fa) continue;
ans = min(ans, dfs2(v, u, rt));
}
return ans;
}
void solve()
{
int i, j;
for (i = 0; i < n; i++)
dfs1(i, -1, i);
for (i = 0; i < n; i++)
{
for (j = 0; j < edges[i].size(); j++)
{
int v = edges[i][j];
best[i][v] = best[v][i] = dfs2(v, i, i);
}
}
}
void query()
{
cin >> q;
int u, v, w;
double sum = 0;
for (int i = 1; i <= q; i++)
{
scanf("%d%d%d", &u, &v, &w);
if (pre[u] != v&&pre[v] != u)
sum += dis_max*1.0;
else
sum += dis_max*1.0 - map[u][v] + min(best[u][v], w);
}
printf("%.4f\n", sum / q);
}
int main()
{
int u, v, w;
while (~scanf("%d%d", &n, &m) &&n + m)
{
init();
for (int i = 0; i < m; i++)
{
scanf("%d%d%d", &u, &v, &w);
map[u][v] = map[v][u] = w;
}
prim();
solve();
query();
}
return 0;
}End