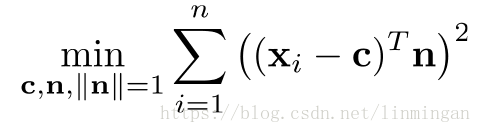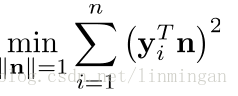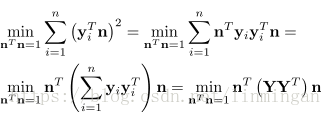3D【24】PCA点云法向量估计

点云法向量的估计在很多场景都会用到，比如ICP配准，以及曲面重建。

基于PCA的点云法向量估计，其实是从最小二乘法推导出来的。假设我们要估计某一点的法向量，我们需要通过利用该点的近邻点估计出一个平面，然后我们就能计算出该点的法向量。或者可以这么说，通过最小化一个目标函数（要求的参数为法向量），使得该点与其每个近邻点所构成的向量与法向量的点乘为0，也就是垂直：

正常情况下，我们可以将点c看成是某一领域中所有点的中心点：

$$m=\frac{1}{n}\sum_{i=1}^{n}X_i$$

同时：

$$y_i=X_i-m$$

这样，优化目标函数变为：

我们进一步对目标函数进行推导：

上面的优化目标函数等于：

$$f(n)=n^TSn 其中，S=(YY^T) \\ min(f(n))\\ s.t. n^Tn=1$$
其中， $YY^T$ 是一个3×3的协方差矩阵，x，y，z坐标的协方差矩阵。
对于这种有约束的优化目标函数，我们可以用拉格朗日算法进行求解：

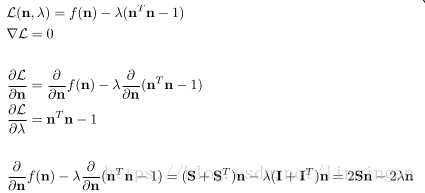
$Sn=\lambda n$?有没有很眼熟，其实就是线性代数里面的特征值和特征向量的相关公式。也即是，$\lambda$ 是矩阵S的特征值，法向量是对应的特征向量。

所以法向量n的求解就是要对S进行向量分解。然后取特征值最小的特征向量作为求解的法向量。这个过程也就是PCA的一个标准求解过程，将每个邻域点与该邻域的中心点相减，得到一个n×3的矩阵。接着，用SVD对该矩阵进行分解，得到：

$$Y=U \Sigma V^*$$

U中最后一列就是要求解的法向量n，也就是特征值最小的特征向量。

为什么是特征值最小的？我个人理解是：PCA的协方差矩阵的特征值越大，其特征向量就越能够描述数据的特征。越小就越不能区分样本之间的不同，也就是表征了数据中的共性。在我们的优化目标函数中，就是要为所有的邻域点寻找一个平面，使得所有的邻域点都在这个平面上，或者说所有点与该平面的距离最小，而不是而不是最大。而这个平面就是能够描述这些点的共性，即他们的法向量都一样。

也可以用另外一个求法，直接对协方差矩阵S，求解特征值和特征向量，然后取最小的特征值对应的特征向量。另外，也不一定用中心点m作为c，可以用点云中要求解法向量的顶点作为顶点c。