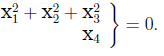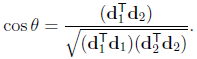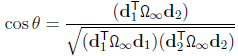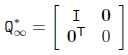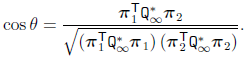1. 三维变换的分类
2. 无穷面
在平面投影上,辨识无穷线 l∞ 即可进行仿射度量,辨识无穷线 l∞ 上的虚圆点I和J即可进行进行相似度度量。类似的,在三维空间的投影变换上,辨识无穷面 π∞ 即可进行仿射度量,辨识绝对二次曲线 Ω∞ 则可进行相似度度量。
在三维空间中位于无限远的平面 π∞ 具有归一化形式 π∞ = (0, 0, 0, 1)T。
定理1:两个平面平行,当且仅当它们的交线位于无穷面 π∞ 上。
平面 π 与 π∞ 的交线,是位于平面π 上的无穷线 l∞ 。
定理2:一条直线平行于另外一条直线或平面,如果它们的交点位于无穷面 π∞ 上。
由此,我们可以说在空间 P3 中,任意两个平面都相交于一条直线。无穷面 π∞ 代表了在投影坐标系中测量仿射属性所需要的3个自由度,它在仿射变换下是固定不动的。
定理3:无穷面 π∞ 在仿射变换 H 下固定不动,当且仅当 H 是仿射变换。
在三维投影变换中进行仿射校正。
- 由两个平行平面的投影确定其交线(即 l∞ 的投影);
- 由两个这样的交线确定一个平面(即 π∞ 的投影);
- 求解变换矩阵 H,将该平面变换为其归一化形式 π∞ = (0, 0, 0, 1)T;
- 利用矩阵 H 对投影场景进行变换,重建的场景是世界场景的仿射变换。
3. 绝对二次曲线
定义(绝对二次曲线,absolute conic):绝对二次曲线 Ω∞ 是位于 π∞ 上的二次曲线。
在归一化的 π∞ = (0, 0, 0, 1)T上,绝对二次曲线 Ω∞ 上的各点满足
对于X4 = 0 的点(方向向量),上式可以写作:
(X1, X2, X3) I (X1,X2,X3)T = 0
可见,Ω∞对应于二次曲线 C = I. 因此Ω∞ 是在平面 π∞ 上由纯虚点构成的二次曲线。Ω∞代表在仿射坐标系中测量相似性属性所需要的5个额外的自由度,它在相似性变换下是固定不动的。
定理4:绝对二次曲线 Ω∞ 在投影变换 H 下固定不动,当且仅当 H 是一个相似性变换。
绝对二次曲线 Ω∞ 的性质:
- Ω∞在相似性变换下固定不动,但不是点对点的固定。
- 因为任意平面 π 与 π∞ 交于一条直线, 而这条直线与Ω∞相交于两个点,所以,所有的圆都与Ω∞相交于两个点。
- 所有球面与 π∞ 相交于Ω∞。
两条直线的夹角。在欧式空间中,设有两条直线,它们的方向向量是 d1 和 d2(3维向量),则它们之间的夹角为
而在投影空间中,它们之间的夹角为
其中Ω∞是绝对二次曲线的投影。
相似性校正。两条直线正交意味着d1TΩ∞ d2 = 0,可以利用多个正交对求得Ω∞投影,进而进行相似性校正。
4. 绝对二次曲面
绝对二次曲线 Ω∞ 是位于 无穷面 π∞ 上的二次曲线, Ω∞ 的对偶是3维空间中的一个退化的二次曲面,叫做绝对二次曲面(absolute dual quadric),记作Q*∞。在几何上,Q*∞包含所有与Ω∞相切的平面。Q*∞用一个4x4齐次方程表示:
定理5:绝对二次曲面Q*∞在投影变换 H 下固定不动,当且仅当 H 是个相似性变换。
定理6:无穷面 π∞ 是Q*∞的零空间。
对于归一化的Q*∞ 和归一化π∞ = (0, 0, 0, 1)T的,显然有 Q*∞π∞ = 0。在投影空间中,仍然有
Q*'∞π'∞ = (H Q*∞ HT)H-T π∞ = 0
平面夹角。两个平面π1和π2之间的夹角定义为
在投影空间中,只要求得投影后的Q*∞,则两个平面之间的夹角可以直接由上式求出。