最大流模板对偶图bzoj1001费用流模板最小点覆盖集最小点权覆盖集最大点独立集最大点权独立集最大权闭合子图最小路径覆盖
网络流定义
- 在一个有向图上选择一个源点,一个汇点,每一条边上都有一个流量上限,即经过这条边的流量不能超过这个上界,同时,除源点和汇点外,所有点的入流和出流都相等,而源点只有流出的流,汇点只有汇入的流。这样的图叫做网络流。
- 源点:只有流出去的点
- 汇点:只有流进来的点
- 流量:一条边上流过的流量
- 容量:一条边上可供流过的最大流量
- 残量:一条边上的容量-流量
性质:
- 对于任何一条流,总有流量<=容量
- 对于任何一个不是源点或汇点的点u,总有
∑p∈Ek[p][u]==∑q∈Ek[u][q]- 一个点(除源点和汇点)的入流和出流相等
- 对于任何一条有向边(u,v),总有
k[u][v]==−k[v][u]- 一条边的反边上的流是这条边的流的相反数.(如果有k[u][v]的流从u流向v,也就相当于有-k[v][u]的流从v流向u.)
引入网络最大流
网络最大流
定义: 网络流的最大流算法就是指的一个流量的方案使得网络中 流量最大(即流到汇点的最大的流量).
如何求解
增广路思想
- 找到一条从源点到汇点的路径,使得路径上任意一条边的残量>0(注意是小于而不是小于等于,这意味着这条边还可以分配流量),这条路径便称为增广路
- 找到这条路径上最小的F[u][v](我们设F[u][v]表示u->v这条边上的残量即剩余流量),下面记为flow
- 将这条路径上的每一条有向边u->v的残量减去flow,同时对于起反向边v->u的残量加上flow(为什么呢?我们下面再讲)
- 重复上述过程,直到找不出增广路,此时我们就找到了最大流
特殊情况
当我们在寻找增广路的时候,在前面找出的不一定是最优解,如果我们在减去残量网络中正向边的同时将相对应的反向边加上对应的值,我们就相当于可以反悔从这条边流过。
但是我们的增广过程是非常混乱的,是相当于不停地找增广路,如果不是最优的就疯狂删边,岂不是很浪费时间,所以我们有更好的算法
Dinic !!
为了解决我们上面遇到的低效方法,Dinic算法引入了一个叫做分层图的概念。具体就是对于每一个点,我们根据从源点开始的bfs序列,为每一个点分配一个深度,然后我们进行若干遍dfs寻找增广路,每一次由u推出v必须保证v的深度必须是u的深度+1.
变量的定义:
int s,t;//源点和汇点
int cnt;//边的数量,从0开始编号。
int Head[maxN];//每一个点最后一条边的编号
int Next[maxM];//指向对应点的前一条边
int V[maxM];//每一条边指向的点
int W[maxM];//每一条边的残量
int Depth[maxN];//分层图中标记深度Dinic
int Dinic()
{
int Ans=0;//记录最大流量
while (bfs())
{
while (int d=dfs(s,inf))
Ans+=d;
}
return Ans;
}dfs过程
bool bfs()
{
queue<int> Q;//定义一个bfs寻找分层图时的队列
while (!Q.empty())
Q.pop();
memset(Depth,0,sizeof(Depth));
Depth[s]=1;//源点深度为1
Q.push(s);
do
{
int u=Q.front();
Q.pop();
for (int i=Head[u];i!=-1;i=Next[i])
if ((W[i]>0)&&(Depth[V[i]]==0))//若该残量不为0,且V[i]还未分配深度,则给其分配深度并放入队列
{
Depth[V[i]]=Depth[u]+1;
Q.push(V[i]);
}
}
while (!Q.empty());
if (Depth[t]==0)//当汇点的深度不存在时,说明不存在分层图,同时也说明不存在增广路
return 0;
return 1;
}dfs过程
int dfs(int u,int dist)//u是当前节点,dist是当前流量
{
if (u==t)//当已经到达汇点,直接返回
return dist;
for (int i=Head[u];i!=-1;i=Next[i])
{
if ((Depth[V[i]]==Depth[u]+1)&&(W[i]!=0))//注意这里要满足分层图和残量不为0两个条件
{
int di=dfs(V[i],min(dist,W[i]));//向下增广
if (di>0)//若增广成功
{
W[i]-=di;//正向边减
W[i^1]+=di;反向边加
return di;//向上传递
}
}
}
return 0;//否则说明没有增广路,返回0
}完整代码
#include <iostream>
#include <cstdio>
const int maxM = 200007;
const int maxN = 10007;
int s,t,n;//源点和汇点
int cnt;//边的数量,从0开始编号。
int Head[maxN];//每一个点最后一条边的编号
int Next[maxM];//指向对应点的前一条边
int V[maxM];//每一条边指向的点
int W[maxM];//每一条边的残量1
int Depth[maxN];//分层图中标记深度
void init(int nn,int ss,int tt) {//初始化
n=nn;
s=ss;
t=tt;
cnt=-1;
memset(Head,-1,sizeof(Head));
memset(Next,-1,sizeof(Next));
return;
}
void _Add(int u,int v,int w){
cnt++;
Next[cnt]=Head[u];
V[cnt]=v;
W[cnt]=w;
Head[u]=cnt;
}
void Add_Edge(int u,int v,int w){//加边,同时加正向和反向的
_Add(u,v,w);
_Add(v,u,0);
}
bool bfs()
{
queue<int> Q;//定义一个bfs寻找分层图时的队列
while (!Q.empty())
Q.pop();
memset(Depth,0,sizeof(Depth));
Depth[s]=1;//源点深度为1
Q.push(s);
do
{
int u=Q.front();
Q.pop();
for (int i=Head[u];i!=-1;i=Next[i])
if ((W[i]>0)&&(Depth[V[i]]==0))//若该残量不为0,且V[i]还未分配深度,则给其分配深度并放入队列
{
Depth[V[i]]=Depth[u]+1;
Q.push(V[i]);
}
}
while (!Q.empty());
if (Depth[t]==0)//当汇点的深度不存在时,说明不存在分层图,同时也说明不存在增广路
return 0;
return 1;
}
int dfs(int u,int dist)//u是当前节点,dist是当前流量
{
if (u==t)//当已经到达汇点,直接返回
return dist;
for (int i=Head[u];i!=-1;i=Next[i])
{
if ((Depth[V[i]]==Depth[u]+1)&&(W[i]!=0))//注意这里要满足分层图和残量不为0两个条件
{
int di=dfs(V[i],min(dist,W[i]));//向下增广
if (di>0)//若增广成功
{
W[i]-=di;//正向边减
W[i^1]+=di;//反向边加
return di;//向上传递
}
}
}
return 0;//否则说明没有增广路,返回0
}
int Dinic()
{
int Ans=0;//记录最大流量
while (bfs())
{
while (int d = dfs(s,inf))
Ans+=d;
}
return Ans;
}
int main() {
}二分图
定义: 二分图又称作二部图,是图论中的一种特殊模型。 设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G为一个二分图。 ——摘自度娘百科
通俗来讲就是两个集合,其中集合中的任何一个元素不与这个集合中的其他元素连边,只与另一个集合连边.
举个例子:飞行大队有若干个来自各地的驾驶员,专门驾驶一种型号的飞机,这种飞机每架有两个驾驶员,需一个正驾驶员和一个副驾驶员。由于种种原因,例如相互配合的问题,有些驾驶员不能在同一架飞机上飞行,问如何搭配驾驶员才能使出航的飞机最多.
如下图所示:
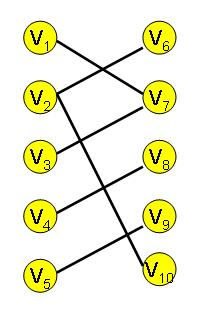
解法
可以利用最大流,流量就是1,最后的最大流就是最多匹配的对数,因此,我们可以给他建一个S(原点),T(汇点),分别将两个集合连起来即可.形成了这个样子(画的有些丑,qwq)
对偶图
对偶图这个概念,还是做bzoj 1001 看题解得到的新名词.大概就是这个样子.
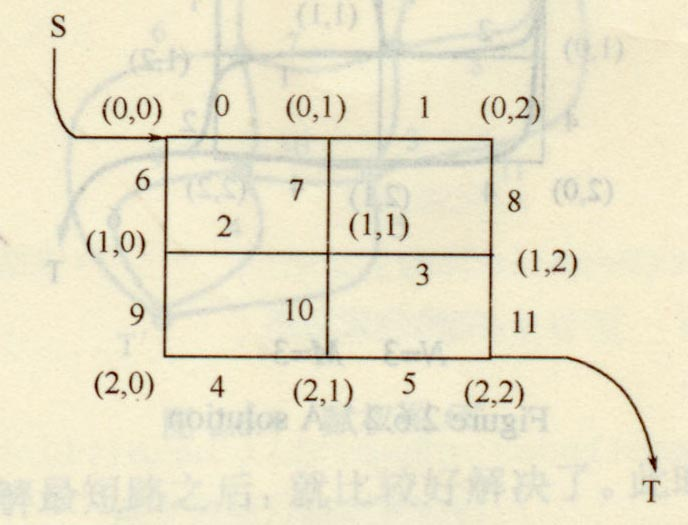 ;
;
让我们去求这个矩阵的最大流.当然,用最大流当然可以,但是时间复杂度不可以保证,所以我们用到一个新的东西,最小割
最小割
定义 最小割就是求最小切取边长为多少的边,才能让整张图不连通
性质: 最小割 = 最大流
所以我们可以用一些最小割的性质来解决这道问题。对于每一条边i新增与它交叉的边j,如果j被经过,就说明i被割掉了,然后建图跑最短路。
如何理解性质:最大流不可能大于最小割, 因为最大流所有的水流都一定经过最小割那些割边, 流过的水流怎么可能比水管容量还大呢? 2.最大流不可能小于最小割, 如果小, 那么说明水管容量没有物尽其用, 可以继续加大水流.
费用流
定义 费用流问题就是在最大流的基础上,每条边不光有容量,还有费用,我们需要在保证最大流的同时使 $Σ流量*费用$ 最小。
#include <bits/stdc++.h>
#include <queue>
const int MAXN=2000001;
const int maxn=0x3f3f3f3f;
using namespace std;
struct node {
int u,v,flow,spend,nxt;
}edge[MAXN];
int head[MAXN];
int num;
int n,m,s,t;
int ans,maxflow;
int dis[MAXN];
int vis[MAXN];
int from[MAXN];
void add_edge(int x,int y,int z,int c)
{
edge[num].u=x;
edge[num].v=y;
edge[num].flow=z;
edge[num].spend=c;
edge[num].nxt=head[x];
head[x]=num++;
}
bool SPFA()
{
memset(dis,0x3f3f3f3f,sizeof(dis));
memset(vis,0,sizeof(vis));
dis[s]=0;
queue<int> q;
q.push(s);
vis[s]=1;
while(!q.empty())
{
int p=q.front();
q.pop();
vis[p]=0;
for(int i=head[p];i!=-1;i=edge[i].nxt)
{
if(dis[edge[i].v]>dis[edge[i].u]+edge[i].spend&&edge[i].flow>0)
{
dis[edge[i].v]=dis[edge[i].u]+edge[i].spend;
from[edge[i].v]=i;
if(!vis[edge[i].v])
{
vis[edge[i].v]=1;
q.push(edge[i].v);
}
}
}
}
if(dis[t]!=maxn)
return 1;
else
return 0;
}
void f()
{
int mn=maxn;
for(int i=t;i!=s;i=edge[from[i]].u)
mn = min(mn,edge[from[i]].flow);
for(int i = t;i != s;i = edge[from[i]].u)
{
edge[from[i]].flow-=mn;
edge[from[i]^1].flow+=mn;
ans+=(mn*edge[from[i]].spend);
}
maxflow+=mn;
}
int main()
{
n=read();m=read();s=read();t=read();
memset(head,-1,sizeof(head));
for(int i=1;i<=m;++i)
{
int x=read(),y=read(),z=read(),c=read();
add_edge(x,y,z,c);
add_edge(y,x,0,-c);
}
while(SPFA())
{
f();
}
printf("%d %d",maxflow,ans);
return 0;
}
最小割模型
- 最小点覆盖集(最小点覆盖=最大匹配数)
- 最小点权覆盖集(同上)
- 最大点独立集(最大点独立集=V-最大匹配数)
- 最大点权独立集(同上)
- 最大权闭合子图(总的实验金额减去最小割。)
- 最小路径覆盖(最小路径覆盖=V-最大匹配数)