文章目录
前言
本文是对于算法设计的学习笔记,如有错误,请不吝赐教。
参考:https://www.cnblogs.com/ZJUT-jiangnan/p/3632525.html
一、网络流
这一部分的内容起源于二分匹配问题。
我们可以回顾一下二分匹配问题:给定一个无向图G(V,E),它的节点集合可以划分为X,Y。它的边具有一下性质:每条边e有一个端点属于X,另一个端点属于Y
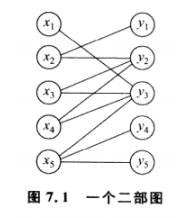
我们在回顾以往的匹配概念:
1.稳定匹配问题
2.序列比对问题。
而在图中,边构成节点的对,因此我们认为图G的一个匹配是边的集合M,每个节点刚好出现在M的一条边上,认为该集合为完美匹配。
二、最大流问题与Ford-Fulkerson算法
2.1 问题
流网络:我们认为流网络是具有一下特征的有向图G(V,E)
1.每条边e关联一个容量,非负,记作ce
2.存在单一源点s
3.存在单一汇点t
除了s,t其他的节点叫做内部节点。
流:s-t流是一个函数f
它把每条边映射到一个非负实数
1.对每个e,都有0<=f(e)<=ce
2.除了s与t之外的每个节点都有:
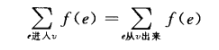
即能量守恒。
最大流问题:给定一个流网络,找出一个具有最大值的流。(使得有效容量尽可能得到有效的使用)
2.2 算法设计
剩余图:
1Gf的节点集与G的节点及相同。
2对G的每条边e=(u,v),其中f(e)<ce,那么存在ce-f(e)的剩余容量大卫,我们
可以尝试在这个容量上向前推流。因此,我们在图Gf中包含这条边e=(u,v),容量为ce-f(e),这种边为前向边
3.对于G的每条边,我们只要想做都可以先后推这个流来撤销他,这种形式的边为后向边。
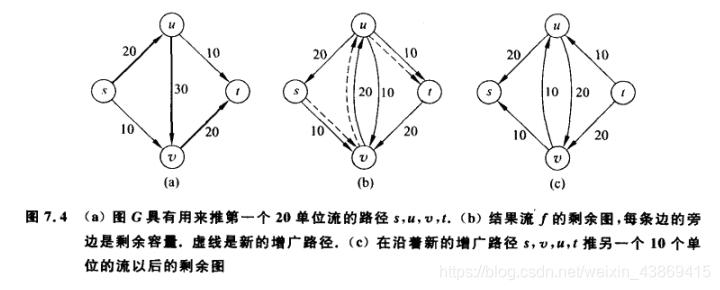
剩余图中的一条边的容量看做剩余容量。
剩余图中的增广路径:
P是图Gf中的一条简单s-t路径
其中bottleneck(P,f)是P上任何边关于流f的最小剩余容量
augment(f,P) 增广操作
令b=bottleneck(P,f)
for 每条边(u,v)属于P
if e=(u,v) 是一条前向边 then
在G中把f(e)增加b
else(u,v)是一套后向边
在G中把f减少b
endif
endfor
return f
上述算法的结果是一个新的流f’
最大流算法(Ford-Fulkerman算法)
Max-Flow
对G中所有的e初始化f(e)=0
while 在增广矩阵Gf中存在一条s-t路径
令P是Gf中的一条简单路径
f'=augment(f,P)
把f更新为f'
把增广图更新为Gf'
endwhile
return f
2.3 算法分析



由该结论可知该算法中的while循环至多迭代C次,
令n表示G中节点数,m表示G中的边数。O(m+n)=O(m)

对于获取一条路径,可以用DFS或者DPS来完成,借助邻接表的存储方式,需要O(m+n),augment操作需要O(n),所以如上结论成立。
三、网络中的最大流与最小割
3.1 问题
s-t割:将结点集合V的一个划分(A,B),使得s属于A,t属于B,一个割的容量记为c(A,B),其等于从A出来的所有边的容量之和。

这也就是说一个流恰好是离开A的总量-返回进入A的总量。
补充:
我们可知内点的进入量和流出量相同。


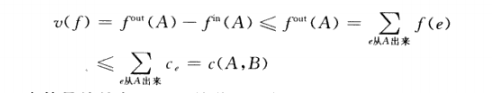
上述定理表达的是每个流的值都是以每个割的容量为上界的。
3.2 分析算法

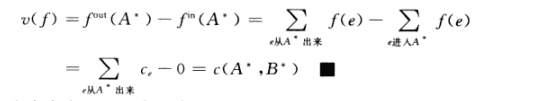
可知A是包含所有S-v路径的点击,B是V-A
由于Ford-Fulkerson算法终止时剩余图不存在s-t路径,故而Ford-Fulkerson返回的流是最大流。

此时我们可以构造一个图Gf,执行DFS或者DPS来确定可以到达的所有点的集合A,然后定义B,并返回割(A,B)


此时返回的割为最小容量割。
3.3 整数值的流
以上的论述中,都是基于流为整数,如果流为实数,那么当增广路径选择不合理是,会使得算法永远运行下去。
四、选择好的增广路径
4.1 问题
在流问题中,如果对于增广路径选择的不合理,会导致算法的迭代次数变得非常多。如何选择一个较好的增广路径需要我们去考虑。
4.2 算法设计
我们维护一个缩放参数△,我们将寻找瓶颈容量至少是△的路径。
Gf(△)是由那些剩余容量至少为△的边组成的剩余图的子集。
算法如下:
Scaling Max-Flow
对G中所有的e初始化f(e)=0
初始化△为2的最大的幂,且不大于从S出来的最大容量
while △>=1
while 图Gf(△)有一条s-t的路径
令P是其中的一条简单s-t路径
f'=augment(f,P)
f=f'
更新Gf△
endwhile
△=△/2
endwhile
return f
4.3 算法分析

我们将外层的while循环即具有固定值△的迭代称作△缩放阶段。我们易知△的初值最多是C,而且不会低于1.故:

对于每个缩放阶段的增广次数,由于我们考虑的是能够大量增广流的路径,因此,增广次数也相对较少。


类似于之前的证明,我们此处也可以得到
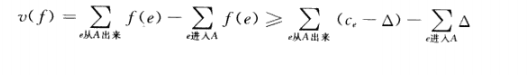



当C较大时,这个时间的界比O(mc)要好的多。
4.4 推广:强多项式算法
当迭代次数与容量的值无关,仅为|v|和|E|的多项式,并且处理的数是字节数的多项式,叫做强多项式算法。
我们可以在每次迭代中选择具有最少边数的增广路径。
五、前向流推动最大流算法
上述算法,我们一直围绕着剩余图中增广路径的来进行相关讨论,这里,我们研究前向流推动算法。
5.1 算法设计
前向流推动算法本质上将以一边接一边的方式来增加流。
前向流:s-t前向流是一个把每条边e映射到非负实数的函数,一个前向流f满足:
1.对于每条边e,都有0<=f(e)<=ce
对于除了s之外的其他节点,进入的流必须至少与出去的流一样多。
2.对除源点s之外的每个其他节点v都有:
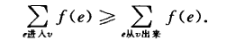
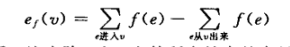
上述的这个差叫做前向流在节点v的余量。
前向流算法维护一个前向流并且将这个前向流转换成一个流。(流自然的能找到它的下坡路)
定义每个节点的高度hv,我们将具有较高标记的节点把流推向较低标记的节点。
当1.ht=0,hs=n
2.对于剩余图中所有边(v,w),都有hv<=hw+1
我们就认为标记h和s-t前向流f是一致的。




如果我们能够在任何存在离开v且通向一个较低高度节点的W的边,那么我们可以从v到w推动某些余量流来修改f,此操作为push

如果无法沿着离开v的边推v的余量,那么我们需要增高v的高度。此操作为重新标记。

完整算法:

5.2 算法分析

对于push和relabel操作的次数:



饱和的push操作:在push操作后,边(v,w)不在处于剩余图中。


5.3 推广:算法的一个改进版本

5.4 实现前向流推动算法
此算法总是选择在最大高度节点实现的方法将以O(n^3)运行
我们可以将具有余量的节点用一个简单的表维护。对于每个可能的高度具有余量的节点的链表。
为了能够很快的选择push,relabel操作的边,我们可以使用图的邻接表表示。对于每个节点,我们在链表中维护在剩余图中离开v的所有可能的边(前向边或者后向边),并对每条边保存它的容量和流值。还需要对于每个节点v维护一个指针current(v),该指针指向表上一个push操作后考虑的边。即当节点v发出一次饱和push操作后,我们把current[v}迁移到这个表的下一条边。

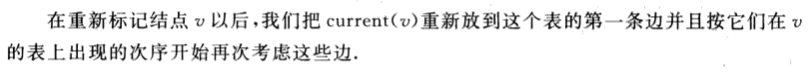
六、二分匹配问题
6.1 问题
二部图G=(v,e)是一个无向图,我们需要找G中的一个最大规模的匹配。
6.2 算法设计
对于二分问题中的图G,我们构造一个流网络G‘,如下所示:
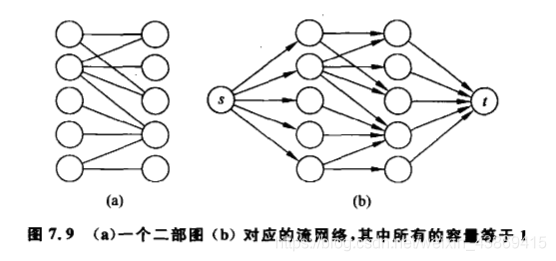
我们将发现网络G‘中的最大s-t流的值等于G中最大匹配的大小。
6.3 算法分析

由于边的容量都为1,
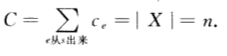

我们这里再考虑增广路径:可以看到所有的增广路径一定在所用的前向边和后向边之间交替进行。(交替路径)这个增广的作用是从匹配中取出所用的后向边,用前向边代替他们,由于s-t,存在的前向边比后向边多一条这也导致了匹配大小+1.
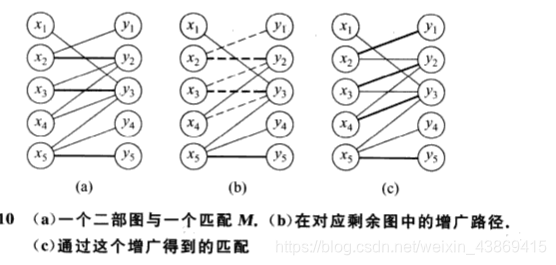
6.4 推广:不具有完美匹配的二部图构造
从上述算法,我们可以找到一个最大匹配然后检查是否是完美的。
那么是否有容易的方法看出一个二部图没有完美匹配呢?
我们可以采用最大流最小割来判断图G是否有完美匹配。

T(A)指的是所有邻接到A中节点的所有节点。
Hall定理:

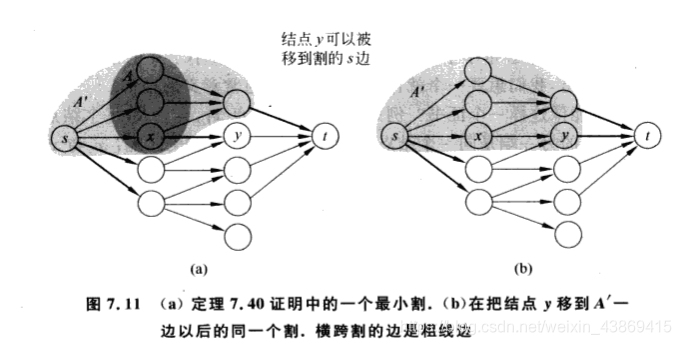
七、在有向与无向图中的不交路径
7.1 问题
我们尝试将流的单位从源点旅行到汇点的理解形式化,得到s-t不交路径的问题。
我们说一组路径是边不交的,如果它们的边集是不交的,即没有两条路径共享同一条边,尽管可能通过某些相同的点。
边不交路径问题即是在图G中找到边不交的s-t路径的最大数目。
7.2 算法设计
我们在有向图中定义一个流网络,使得每条边由容量1.我们假设有k条不交路径,每条路径携带一个流,此时该路径的每条边的流为fe=1,其他的边为fe=0.

7.3 算法分析
为了证明本算法,证明其的逆向命题是这个分析的核心。
我们考虑一个值至少是k的流,并且构造k条边不交路径。

这里可以考虑如果存在(s,u)携带一个单位的流,那么根据流的定义,一定有某条边(u,v)携带一个单位的流。依次下去,要么达到t,要 么再次遇到节点v。
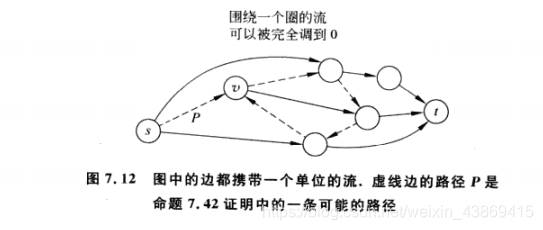




最大流最小割定理对不交路径的解释:如果从G中拿走一组边F以后,图中一套s-t的路径也没剩下,那么我们就说F分离s与t。

上述定理又称(Menger定理)而Hall定理实际上是Menger定理的特殊情况。
7.4 推广:在无向图的不交路径
我们通过将无向图G中的每条无向边(u,v)用两条有向边(u,v)和(v,u)代替,以此来构造一个G的有向图G‘。



八、对最大流问题的推广
最大流问题可以是许多具有重要组合搜索成分的问题在多项式求解。
8.1 问题:带需求的流通
我们这里假设有着一组生成流的源点s和一组能够吸收流的汇点t,此时不再考虑最大流,而是考虑通过有效供给来满足所有需求。
现给出一个边上有容量的流网络G=(V,E),对于每个节点v属于V相关的需求dv,如果dv>0,这表明节点v对于流有dv的需求,如果这个节点市汇点,它希望接收的流比发送的流多dv单位。相反类似。如果节点dv=0,那么节点v既不是源点也不是汇点。
我们说带需求dv的流通是一个函数f,它对每条边分配一个非负的实数,且满足以下条件:
1.对于每个e,都有fe>=0,<=c
2.对每个v,都有fin v-fout v=dv
此时我们仅考虑是否存在一个满足上述条件的流通。
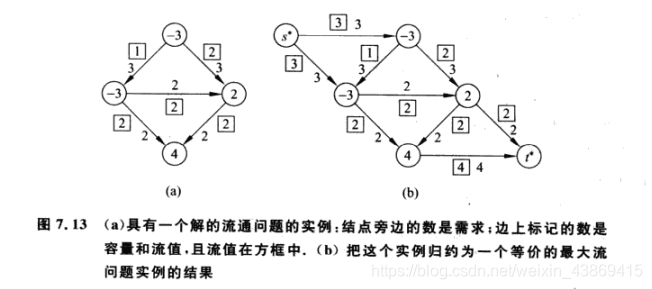

8.2 算法设计
我们对于S中的每个节点加一个超源节点,对于T中的每个节点加一个超汇聚节点。
如下图所示:
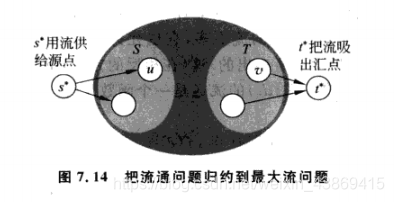
此时我们寻找一个最大的s*-t*流。


8.3 问题:带需求和下界的流通
我们考虑每条边具有容量ce和下界le的流网络。同样每个节点也有需求dv。
故而我们流网络中的流通必须满足一下条件:
1.对于每个e,我们有le<=fe<=ce
2.对于每个v,我们有finv-foutv=dv
我们同样想确定是否存在这样的可行解。
8.4 算法设计
我们的策略是把这个问题归纳为一个求带需求但是没有下界的流通问题。因此我们假设零f0e=le定义一个初始的流通f0.
此时我们再构造图,使其容量为ce-le,节点v的需求是dv-lv
这样问题就变为了求一个带需求但没有下界的流通问题。
如下图所示:
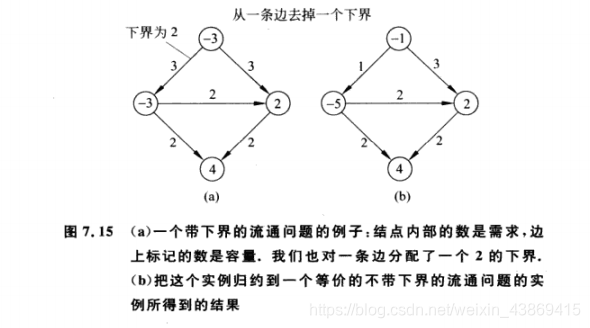

九、调查设计
9.1 问题
我们考虑一家公司,向他的一组特定的n个顾客发放调查表,已确定人们喜欢哪些产品。
具体方针如下:

9.2 算法设计
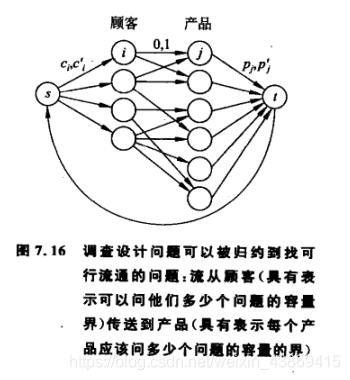

我们可知顾客i参与产品j的调查,当且仅当变(i,j)带一个单位的流。
十、航线调度
10.1 问题
详细见书P277
10.2 算法设计

10.3 算法分析

对于每条流为1的边我们可以分配一架飞机来执行相关的航班。
10.4 推广
上述的算法只是对于航线调度的一个非常简单的问题。再实际中,我们还需要考虑飞机的维护问题等等,我们可以将不同的优化指标加入到算法中,以完善相关的问题。
十一、图像分割
11.1 问题
图像分割问题可以通过最小割的计算来有效求解。比如前景和背景的分割。
我们设V是我们的像素集合,e表示所有相邻像素对的集合。
此处我们给定每个像素属于前景的可能性a和属于背景的可能性b。
那么此时的问题就演变为了一个求最有标记的问题。
11.2 算法设计

我们建立一个超源点以及一个超汇点。并将ai,bi分别定义为与源点和汇点间的容量。同时我们将变(i,j)用两条有向边来建模。
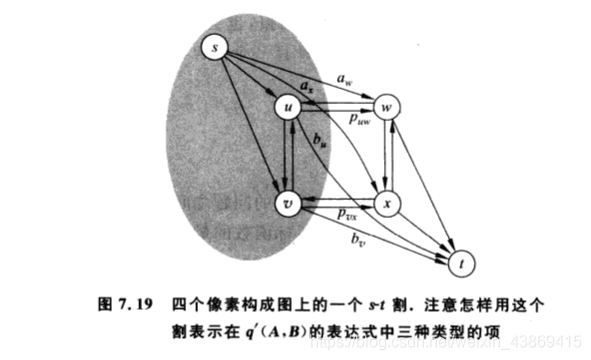

十二、项目选择(露天矿挖掘问题)
12.1 问题
存在一组基本的项目P,每个项目都有相关的收益pi,有可能为正,有可能为负。其中某些项目对于其他项目是先决条件。
项目选择问题就是选择一组具有最大利润的可行项目。
项目的集合A是可行,如果A中的每个项目的先决条件也属于A那么这种形式的先决条件叫做优先约束。
一组项目的利润定义为:
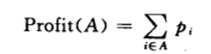
12.2 算法设计
类似于上节所说的那样,我们同样采用最小割算法,构造图G‘如下:
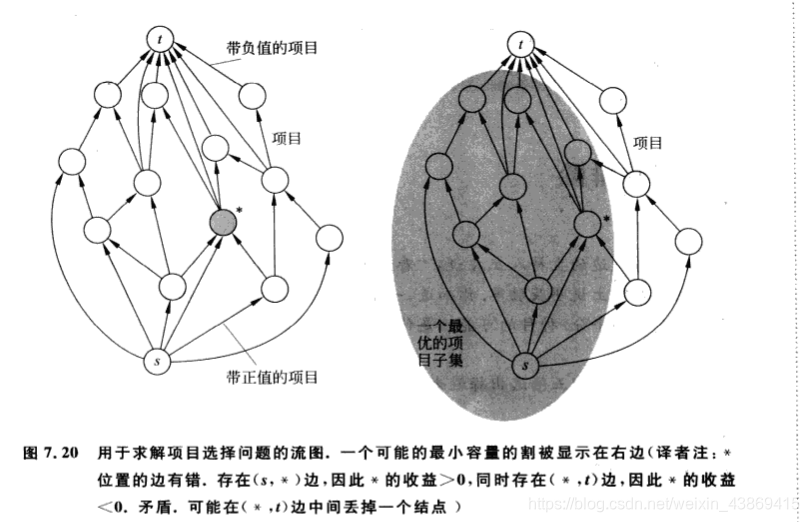
12.3 算法分析


可以证明具有最小容量的割对应于具有最大利润的项目A。

十三、棒球排除
13.1 问题


13.2 算法分析



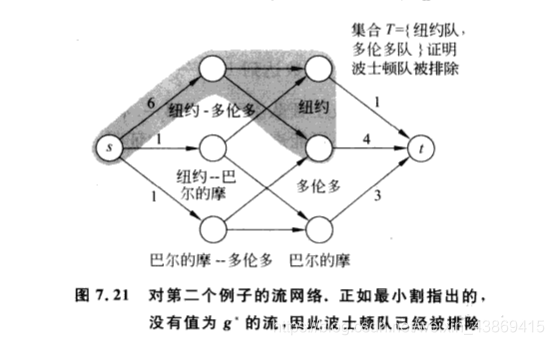

13.3 描述一个队什么时候被排除
十四、进一步的方向:对匹配问题增加费用
14.1 问题
在许多匹配问题的环境中,可能存在大量的完美匹配,所以我们要确定某些完美匹配比其他的要好。
基于此,我们在问题中引入费用。即

14.2 算法设计