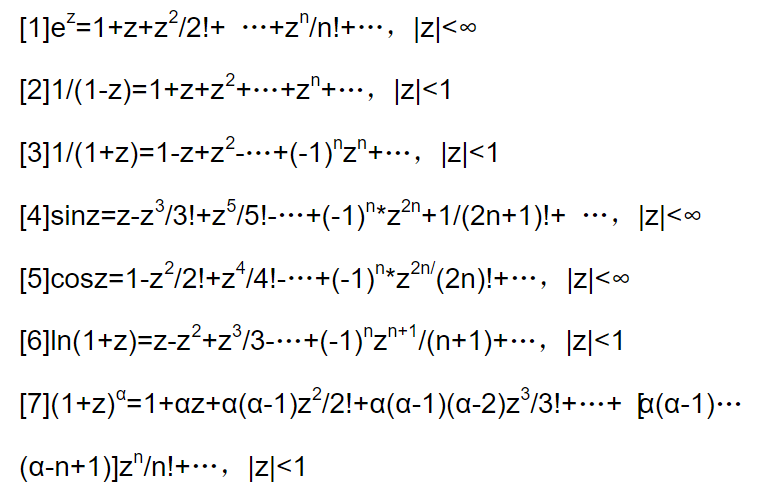正余弦等三角函数定义及基本性质回顾
定义:

运算性质:

向量的定义
一个有长度和方向的矢量,和标量(scalar)相对应
向量的平行(共线),共面和垂直
向量共线平行的充分必要条件是:存在一个标量$ \lambda $ 使得以下成立: $$\vec{a} = \lambda \vec{b}$$
向量共面的充分必要条件是:a,b,c之间存在线性变换关系使得以下成立:$$\vec{c} = \lambda \vec{b}+ \eta \vec{a}$$
向量垂直的充分必要条件是:$$\vec{a} \cdot \vec{b} = 0$$
向量的代数表示
把空间中所有的向量的尾部都拉到坐标原点,这样N维点空间可以与N维向量空间建立一一对应关系:N维点空间中点(0,0,0…0)取作原点,那么每一个点都可以让一个向量和它对应,这个向量就是从坐标原点出发到这个点为止的向量。
向量的内积(数量积,点乘)和外积
内积:两个向量的内积或者叫点乘结果是一个标量,其值等于a,b的模乘以其夹角的cos值。
$\overrightarrow{a} \cdot \overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cos(\overrightarrow{a},\overrightarrow{b})$
如果使用平面直角坐标系来表示,则其值等于坐标分别相乘后相加
$\overrightarrow{a} \cdot \overrightarrow{b}= x_1x_2+y_1y_2+z_1z_2$
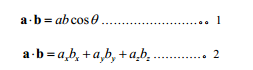
向量内积的几何意义
$\vec{u} \cdot \vec{v}$ 在几何上就是向量$\vec(u)$向向量$\vec{v}$做投影后再乘以$\vec{v}$的长度,就是一个向量在另一个向量上的投影d的积,也就是同方向的积
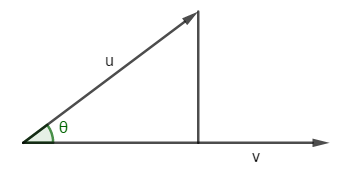
实际上上面向量内积几何意义反过来可以用来计算投影d: $ d = \frac{\vec{u} \cdot \vec{v}}{|\vec{v}|} $

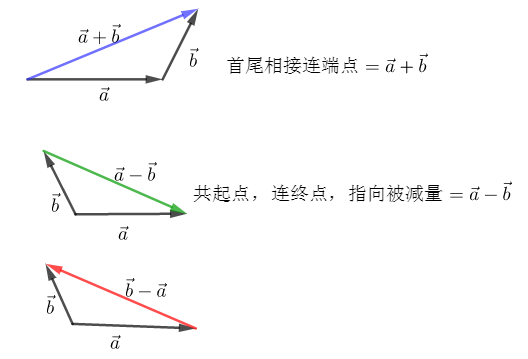
向量加减法几何示意图
向量模计算及不等式
对于起始于原点(0,0)的单点向量$\vec{OA}$,其计算公式为:
$$\vec{a}| = |\vec{OA}| = \sqrt{ \vec{a} \cdot \vec{a} } = \sqrt{x_A^{2}+y_A^{2}+...+z_A^{2}}$$
对于由空间两点A和B组成的向量,则需要先做对应坐标相减,再按照起始于原点的向量模计算公式来计算
$$|\vec{AB}| = \sqrt {\vec{AB} \cdot \vec{AB}} = |\vec{OA} - \vec{OB}| = |\vec{OC}| = \sqrt{(x_a-x_b)^{2}+(y_a-y_b)^{2}+...+(z_a-z_b)^{2}}$$
其中$C$点的坐标为$(x_A-x_B,y_A-y_B,z_A-z_B)$ (也可以简单地说$\vec{AB}$的坐标),也就是说向量$\vec{c} = \vec{OC}$ 是由自由变量$\vec{AB}$变换为经过欧式空间原点的单点向量$\vec{c}$,这样就好计算其模了
$$||\vec{a}| - |\vec{b}| |\leqslant | \vec{a} - \vec{b} |\leqslant | \vec{a}|+|\vec{b}|$$
$$||\vec{a}| - |\vec{b}| |\leqslant | \vec{a} + \vec{b} |\leqslant | \vec{a}|+|\vec{b}|$$
向量的叉乘(外积,向量积)
叉乘,也叫向量的外积、向量积。两个向量叉乘的结果仍为一向量,不妨设为(x3,y3,z3)。向量c的方向与a,b所在的平面垂直,且方向要用“右手法则”判断(用右手的四指先表示向量a的方向,然后手指朝着手心的方向摆动到向量b的方向,大拇指所指的方向就是向量c的方向)。大小为:
$\overrightarrow{a} \times \overrightarrow{b}= |\overrightarrow{a}| |\overrightarrow{b}| sin(\overrightarrow{a},\overrightarrow{b}) $
其向量坐标表示为:
$\overrightarrow{c} = (x,y,x) = (y1z2-z1y2, z1x2-x1z2, x1y2-y1x2)$
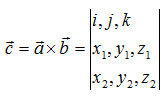
泰勒展开式
泰勒公式是将一个在x=x0处具有n阶导数的函数f(x)利用关于(x-x0)的n次多项式来逼近函数的方法。
$$f(x) = \frac{f(x_0)}{0!} + \frac{f^{'}(x_0)}{1!}(x-x_0) + \frac{f^{''}(x_0)}{2!}(x-x_0)^{2} + \frac{f^{'''}(x_0)}{3!}(x-x_0)^{3}+... + \frac{f^{n}(x_0)}{n!}(x-x_0)^{n}+R_n(x)$$
其中$R_n(x)$是$(x-x_0)^{n}$的高阶无穷小
通常,我们在x0 = 0 处展开,将$f(x_0),f^{'}(x_0),...,f^{n}(x_0)$的值带入泰勒展开式就得到
$$f(x) = \frac{f(0)}{0!} + \frac{f^{'}(0)}{1!}x + \frac{f^{''}(0)}{2!}x^{2} + \frac{f^{'''}(0)}{3!}x^{3}+... + \frac{f^{n}(0)}{n!}x^{n}+R_n(x)$$
在实际科学计算中,我们通过二阶泰勒展开,就可以对$f(x)$实现近似计算
常用函数的泰勒展开