1. 写在前面
最近在看视频跟踪方面的一些硕博士毕业论文,几乎看到的每一篇都会涉及到粒子滤波算法,所以这段时间花了很多时间在看相关的内容。
浏览了大量的博客和文章,跟着不停推导公式,感觉还是无法完全掌握,无法将这个抽象的数学模型和实际应用中联系起来,不过随着时间推移,推导的更多,思考的更多,理解的也越来越透彻了,这里做一下笔记,一方面整理一下思路加深自己的理解,另一方面也给这篇文章的读者提供一些参考。
其实有些地方确实比较难以理解,我在看相关资料的时候发现有一些内容和推导都是直接一笔带过,我也花了不少时间一点一点推导和理解。这篇文章,笔者将尽自己所能把整个过程说的完整详细,但是限于自己水平有限,如果有什么说的不好的或者理解有问题的地方,请指正,谢谢。
2. 本文结构
本文将从贝叶斯滤波入手,进而从蒙特卡洛方法,重要性采样,序贯重要性采样,重采样等等方法一步一步阐述基本粒子滤波的完整推导过程,最终会给一个完整的基本粒子滤波的实现流程。据我的理解,整个粒子推导的过程其实就是在解决当前问题的时候挖一个坑,然后在解决这个坑的同时继续挖坑,然后继续解决,直到最后得到一个比较完善的算法框架。
3. 正文
粒子滤波通过非参数化的蒙特卡洛(Monte Carlo)模拟方法来实现递推贝叶斯滤波,适用于任何能用状态空间模型描述的非线性系统,精度可以逼近最优估计。粒子滤波器具有简单、易于实现等特点,它为分析非线性动态系统提供了一种有效的解决方法,从而引起目标跟踪、信号处理以及自动控制等领域的广泛关注。
3.1 贝叶斯框架下的跟踪问题描述
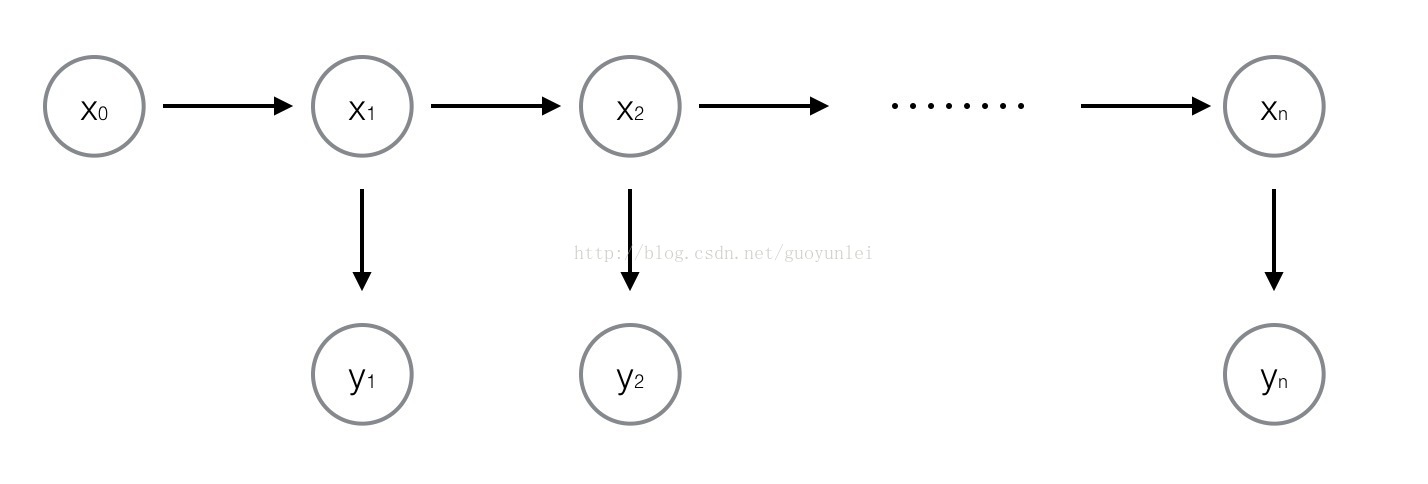
为了描述跟踪问题,我们定义目标状态空间方程如下:
状态模型 :观测模型:
其中,表示状态,表示观测,表示动态噪声或过程噪声, 表示观测噪声。
系统简易模型如下图所述所示:
所以从贝叶斯角度,跟踪问题即为: 从 中推导出即后验概率密度。
假设已知,那么通过以下递推得到:
预测:
跟新:
式中:
为状态转移概率,由目标状态模型定义。
为观测模型定义,也称为观测似然度。
为归一化常数:
注释:
- 预测步用柯尔莫哥洛夫-切普曼方程(C-K方程)得到。
- 跟新步的完整推导如下:
所以,在贝叶斯框架下的跟踪问题即贝叶斯滤波推导完成了,上述推导使用了定积分,当系统处于线性、高斯假设条件下,可以得到解析解,此时即为著名的卡尔曼滤波(关于卡尔曼滤波的讨论又是另一个话题了,这里不多说,以后有机会会详细讨论),但是在实际使用中,大多情况下均为非线性非高斯系统,就很难得到解析解,所以接下来需要引入蒙特卡罗方法来解决这个问题。
3.2 蒙特卡洛方法
这一节,我们暂时先放下滤波的问题,我们来重点了解一下什么是蒙特卡洛方法。
蒙特卡罗方法于20世纪40年代美国在第二次世界大战中研制原子弹的“曼哈顿计划”计划的成员S.M.乌拉姆和J.冯·诺伊曼首先提出。数学家冯·诺伊曼用驰名世界的赌城——摩纳哥的Monte Carlo——来命名这种方法,为它蒙上了一层神秘色彩。在这之前,蒙特卡罗方法就已经存在,1777年,法国数学家布丰(Georges Louis Leclere de Buffon,1707—1788)提出用投针实验的方法求圆周率π,这被认为是蒙特卡罗方法的起源。
简单来说,蒙特卡罗方法就是一种计算方法。原理是通过大量随机样本,去了解一个系统,进而得到所要计算的值。它非常强大和灵活,又相当简单易懂,很容易实现。对于许多问题来说,它往往是最简单的计算方法,有时甚至是唯一可行的方法。
假设 随机变量 服从某个分布 , 那么对于 的一个函数 ,我们有:
若此时我们可以采集到服从分布的一系列样本 ,那么根据蒙特卡洛使用平均值近似代替积分的思想,就有了:
这很容易从伯努利大数定律的角度理解,当样本足够大的时候,我们可以认为上式取等。这就是蒙特卡洛方法的一个简单理解,这里只是为了求解上述定积分问题,所以我们了解到这一步即可。
3.3 蒙特卡洛思想在贝叶斯滤波中的应用
上面说到贝叶斯滤波使用了积分,不易得到解析解,我们只能采用数值方法求解,而蒙特卡洛方法为高维变量的积分问题求解提供了一种可行的逼近解法,所以,本节我们将讨论如何将蒙特卡洛思想应用在贝叶斯滤波中。
首先,假设我们可以从后验概率中采集到个独立样本,那么后验概率的计算可以表示为:
其中,为狄拉克函数(学过《信号与系统》的小伙伴应该比较熟悉,就是冲激响应函数),我们这里用的是离散形式。
对于这个公式,可以借助下面概率分布图像理解:
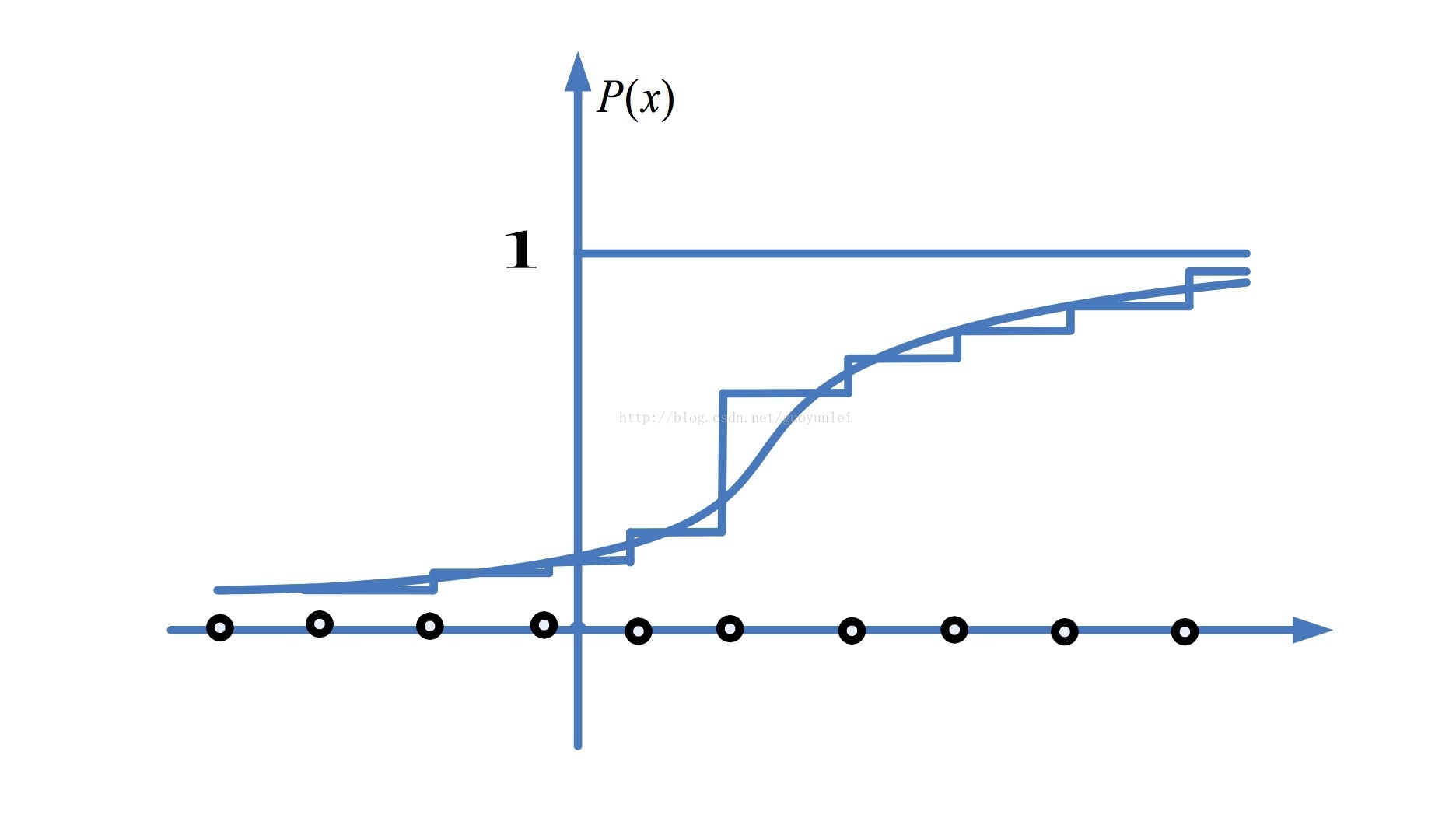
图片来源:百度文库《粒子滤波理论》
从上图很容易看出,使用个独立样本通过蒙特卡洛方法可以近似得到后验概率密度函数,这里的图其实是概率分布图,用这个图只是为了直观表达一下蒙特卡洛思想,自己又太懒没有重新画概率密度函数图,借以理解一下即可。
估计出了后验概率,要做图像跟踪或者滤波,就是要知道当前状态的期望值:
可以看出,只要我们使用采样粒子的状态值的平均就能得到期望值,也就是滤波后的值,这里的就是每个粒子的状态函数。这就是粒子滤波名字的由来了,只要从后验概率中采样很多粒子,用它们的状态求平均就得到了滤波结果。
可是问题出现了,在本节的开头我们假设可以从后验概率中采集到个独立样本,所以说不知道后验概率的情况下从哪里采集样本?这好像就是一个循环的问题了:我们没有后验概率却要从后验概率中采集样本去逼近后验概率和状态期望。别急,接下来就要引出一种用以解决该问题的重要算法:重要性采样。
3.4 重要性采样
这一节主要是介绍重要性采样,这部分有较多的公式推导,请准备好你的纸笔,跟我一起推导吧。
当我们无法从一个未知的分布中采样的时候,重要性采样引入了一个容易采样的重要性概率密度函数,重要性采样的思想就是从这个重要性概率密度函数中采样粒子,然后使用采样的结果去加权逼近我们的后验概率密度函数。下面从两个角度入手进行推导和论证(这两个思路分别来自两篇文献,我觉得两个配合着看可以更好的帮我们理解)。
3.4.1 首先引入一个支撑粒子集 ,其中是从重要性概率密度函数中采样的粒子,表示在时刻第个粒子的状态,是其的权值。
那么后验概率密度函数可以表示为:
其中,
根据蒙特卡洛思想,当采样粒子数目非常大的时候,就可以逼近概率密度函数,那么的期望为:
3.4.2 另一个方面,我们换一个思路,直接求解期望:
其中,表示时刻粒子的权重,和上面的一个意思,只是表示形式不同,且:
又因为
所以,进一步推导如下:
通过这一系列推导我们可以看出最后的期望已经转为完全与有关的期望求解了,这也是这个算法让我叹服的地方。这样我们就可以使用蒙特卡洛方法求解了,所以我们只要个粒子的平均求其期望即可,上面的式子近似为:
这里的为归一化的权值,这个结果其实与上面的结果完全相同,只是一个权值是人为给出来的,一个是推导得出的。
这里我们可以看出来,这里的不是所有粒子的平均值而是所有粒子的加权和,所以每个粒子都有一个权重,可以理解为对当前粒子的信任程度,这样我们就解决了采样的问题,但是这种方法每个新的观测数据都要全部重新计算,这在计算量上是让人崩溃的,下面就引入一种算法来解决这种问题。
3.5 序贯重要性采样
对于上节所述的问题,我们考虑将统计学中的序贯分析方法应用到蒙特卡洛方法中,用以实现后验概率密度的递推估计。
假设重要性概率密度函数为(注意这里是与上一节有所区别),假设该密度函数可以分解如下:
并且需要 声明如下 :
- 系统是一个一阶马尔可夫过程,即:
- 各次观测之间相互独立,即:
那么后验概率密度函数的递推如下:
其中:
- 需要注意这里面的字母大小写所代表的不同含义,在最开始我们已经声明。
- 为归一化常数, 。
这一步按照我的理解,这里面有非常重要的两点需要注意也是上面声明所强调的:
- 状态系统是一个一阶马尔可夫过程,也就是 的状态只与有关。
- 观测值只与有关,由观测模型定义。
所以这样上式就很容易理解了:
- 在中,与并不给提供信息量,所以该项等于
- 在中,同理,和不给提供信息量,所以该项等于
进一步,粒子权值的递归推导为:
当然,这里的推导是没有进行归一化的,我们实际使用的时候需要使用下式进行归一化:
接下来,我们寻找一个合适的重要性概率密度函数:
即重要性分布的只与和有关,则:
所以,我们根据以上的推导,我们就可以总结出序贯重要性采样算法:
采样:从重要性概率密度函数中采集样本
计算:根据最新的观测计算权值
权值归一化,计算估计目标状态
这就是一个基本的序贯重要性采样的推导和算法流程了,但是随着时间的推移,会出现权值退化现象:一些粒子的权值变得非常小,但每次都会占用资源进行计算,这样大量的计算时间浪费在这些不重要的粒子上,导致估计性能下降。
一般来说,我们用有效粒子数来衡量粒子权值的退化程度,有:
上式的意思是:有效的粒子越少,权重方差越大,权值退化越严重。我们在实际计算中,有效粒子近似为:
我们在进行序贯重要性采样的时候,若小于某一设定好的阈值,则应当采取一些措施加以控制。克服序贯重要性采样算法权值退化现象最直接的方法是增加粒子数,而这会造成计算量的相应增加,影响计算的实时性。因此,一般采用以下两种途径:(1)选择合适的重要性概率密度函数;(2)在序贯重要性采样之后,采用重采样方法。
在我看的大多数论文和博客中,都以重采样为主,所以这里我也着重说一下重采样,关于其他方法,读者可以上网查阅相关资料。
3.6 重采样
重采样,简单来说,就是舍弃权值较小的粒子,用新的粒子来代替他们,容易想到的就是将权值较大的粒子多复制几个出来代替它们,复制的原则就是根据权重按比例进行分配。
根据前面的推导我们知道:
我们希望经过重采样以后得到如下结果:
上式符号较多,说明如下:
- 表示的是从重要性密度函数中采样得到的粒子,表示其序号,表示其个数。
- 表示的是重采样以后留下来的不同的粒子,表示其序号,表示其个数,而每一个由于重采样,它的个数为,但是所有例子的总数加起来仍然为。
常用的重采样方法包括多项式重采样、残差重采样、分层重采样与系统重采样等,我们只说一下残差重采样。
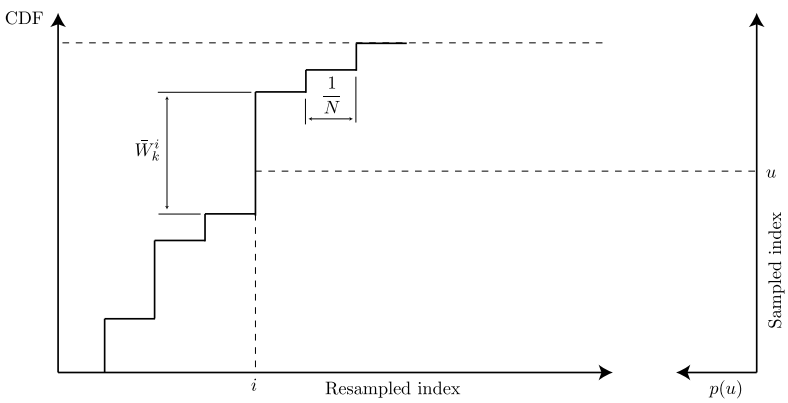
残差重采样流程如下:
- 计算当前概率累计和,也就是概率分布,为
- 生成个在个[0,1]区间均匀分布的随机数
- 对于每个,寻找概率分布中大于或等于的最小标号,即。当落在该区间时,那么被复制一次,最后每个粒子的个数就是这里累计复制的个数。
看起来可能不太直观,我们举个栗子:
假设当前有5个粒子,权值分别为:0.1,0.2,0.2,0.2,0.3
那么当前的概率分布为:0.1,0.3,0.5,0.7,1.0
生成5个在[0,1]中均匀分布的随机数,假设为:0.08,0.27,0.57,0.72,0.9
,,复制一次;
,,复制一次;
,,复制一次;
,,复制一次;
,,复制一次;
所以上面的五个粒子,序号为1,2,4的分别复制一次,序号为5的复制两次,序号为3的复制0次(当然,这个例子不一定准确,因为随机数是我瞎写的)。
给张图感受一下:
图片来源:Particle Filter Tutorial 粒子滤波:从推导到应用(三)
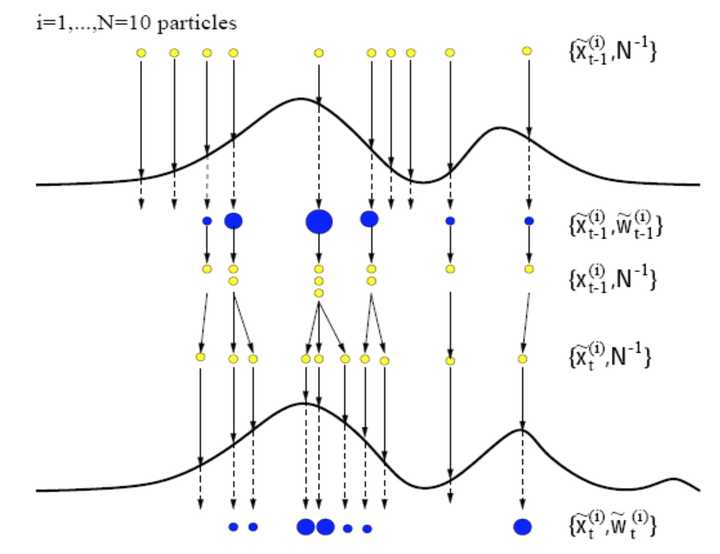
所以SIR算法就如下图所示:
图片来源:百度文库《粒子滤波理论》
3.7 粒子采样算法完整流程
通过以上的叙述,我们可以总结出来一个基本的粒子采样算法的完整流程如下:
1. 粒子集初始化,对 :
对于,由生成采样粒子
2. 对于,执行下面的步骤:
- 重要性采样:从重要性概率密度函数中采集样本,计算他们的权值并归一化
- 重采样:对上一步得到的粒子集进行重采样,得到新的粒子集为
- 输出结果:计算时刻的状态估计值
这就是一个完整的基本的粒子滤波的流程了。
4. 写在最后
粒子滤波本身就是一个比较复杂的算法,我在学习的时候,真正投入的时间加起来得有三四天才完整弄明白这个流程,有几篇博客前前后后看了很多遍,看完一遍若有所思,回头继续看一遍,跟着一遍又一遍推导公式,这样才慢慢理解了这个算法,其中遇到的很多小问题和一些自己的想法我都在正文里体现出来,希望可以给读者一些参考。
本来还想写一个程序能更好帮助理解和使用算法,但是最近时间有限,加之这篇文章的篇幅过大,已经无力继续往下添加内容了,而且最近我还是处于大量阅读论文阶段,所以程序先暂时搁置,等到忙完了,可能会再写一篇关于粒子滤波的应用相关的内容,先给自己立一个flag吧。
每个人的基础和知识框架不同,我在看别人的文章的时候有时候会觉得有些地方比较简单却花了很多篇幅,而有些地方很难理解别人却一笔带过,别人在看我的文章时可能也会有这种感觉,我在写这篇文章的时候,尽可能详细地阐述这个算法并且尽量不放过每一个重点,但是也不能完全保证满足所有人,如果有什么不明白的地方大家可以相互交流讨论。
理解这部分内容花了很多时间,写这篇文章也花了很多时间,前前后后反复看,一个个公式一个个字母都仔细检查,其实这篇文章最开始是用markdown写的,在知乎上又得重新排一下,公式也不是特别好看,最重要的是我不知道知乎的TeX编辑器如何做长连等式的等号对齐,而且默认的右对齐也让人很难受(强迫症表示真的很接受不了,希望有知道的小伙伴可以跟我说一下,谢谢)。
一直以来自己的写作水平有限,可能会有一些地方写的不是很好甚至有错误,如果有什么意见或者建议,不妨提出来,谢谢。
作者:桑燊
2017年5月9日
转载地址:https://zhuanlan.zhihu.com/p/26783371