内容转自博客https://blog.csdn.net/shenziheng1/article/details/52916278
特征值分解
通过特征值分解方阵可以得到特征值与特征向量,特征值表示的是这个特征(即矩阵变换的方向)到底有多重要,而特征向量表示这个特征是什么,即特征值所对应的特征向量就是描述这个矩阵变化方向(从主要的变化到次要的变化排列)。可以将每一个特征向量理解为一个线性的子空间,这些我们可以利用这些线性的子空间干很多的事情。不过,特征值分解也有很多的局限,比如说变换的矩阵必须是方阵。
奇异值分解
是一个能适用于任何矩阵的分解方法,
假设A是一个N * M的矩阵,那么得到的U是一个N * N的方阵(里面的向量是正交的,U里面的向量称为左奇异向量),Σ是一个N * M的矩阵(除了对角线的元素都是0,对角线上的元素称为奇异值),V’(V的转置)是一个M* M的矩阵,里面的向量也是正交的,V里面的向量称为右奇异向量)
那么奇异值和特征值是怎么对应起来的呢?首先,我们将一个矩阵A的转置 * A,将会得到一个方阵,我们用这个方阵求特征值可以得到:
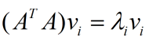
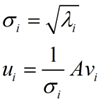
这里的σ就是上面说的奇异值,u就是上面说的左奇异向量。奇异值σ跟特征值类似,在矩阵Σ中也是从大到小排列,而且σ的减少特别的快,在很多情况下,前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上了。也就是说,我们也可以用前r大的奇异值来近似描述矩阵,这里定义一下部分奇异值分解:

r是一个远小于m、n的数,这样矩阵的乘法看起来像是下面的样子:
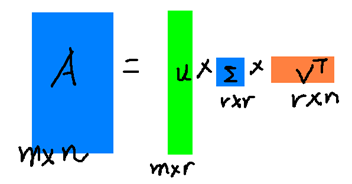
右边的三个矩阵相乘的结果将会是一个接近于A的矩阵,在这儿,r越接近于n,则相乘的结果越接近于A。而这三个矩阵的面积之和(在存储观点来说,矩阵面积越小,存储量就越小)要远远小于原始的矩阵A,我们如果想要压缩空间来表示原矩阵A,我们存下这里的三个矩阵:U、Σ、V就好了。