SVD奇异值分解

正交矩阵

正交矩阵对应着正交变换，特点在于不改变向量的尺寸（模）和任意两个向量的夹角。在x-y坐标系中，通俗地讲，就是旋转两个坐标轴，得到新的互相垂直的坐标轴，求向量在新坐标系中的投影。

正交变换举例

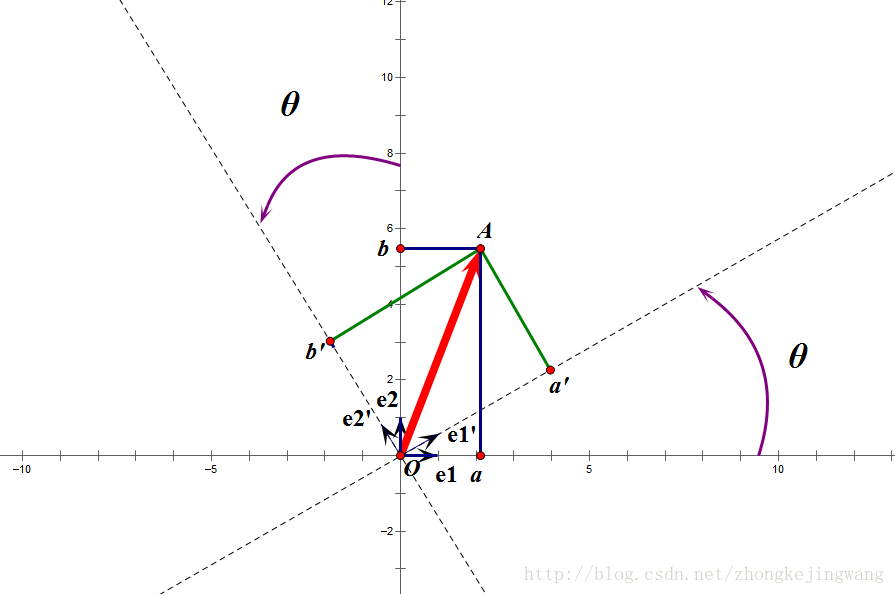
图片摘自此处。例如向量 $OA$ ，在原始 $e_1-e_2$ 坐标系中表示为 $(a,b)^T$ ，在旋转后的坐标系 $e_1'-e_2'$ 中表示为 $(a',b')^T$ ，若存在一个矩阵 $U$ 使得 $(a',b')^T=U(a,b)^T$ ，则矩阵 $U$ 是正交矩阵（可见对应着坐标系之间的正交变换）。
可以代入求得矩阵 $U$ ，且可观察到矩阵的行向量之间都是正交的，列向量之间也是正交的。

U = [\begin{matrix} \cos θ & \sin θ \\ - \sin θ & \cos θ \end{matrix}]

$U=\left[\begin{matrix}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{matrix}\right]$

正交矩阵的性质

正交阵的逆等于其转置

A^{T} A = I \to A^{T} = A^{- 1}

$A^TA=I\rightarrow A^T=A^{-1}$

特征值分解

$A$ 是 $N\times N$ 满秩对称方阵（对称阵的特征向量之间两两正交），有 $N$ 个特征值 $\lambda_i$ ，对应 $N$ 个特征向量 $q_i$ ，有：

{\begin{matrix} A q_{1} = λ_{1} q_{1} \\ A q_{2} = λ_{2} q_{2} \\ \dots \\ A q_{N} = λ_{N} q_{N} \end{matrix}

$\left \{ \begin{matrix} Aq_1=\lambda_1q_1 \\ Aq_2=\lambda_2q_2 \\ \cdots \\ Aq_N=\lambda_Nq_N \end{matrix}\right .$
可以理解为向量

q_{i}

$q_i$ 在

A

$A$ 的作用下，保持方向不变，只进行比例为

λ_{i}

$\lambda_i$ 的缩放。特征向量所在的直线包含了所有特征向量（称为特征空间）。
以上

N

$N$ 个等式写成矩阵形式（

q_{i}

$q_i$ 是

N \times 1

$N\times 1$ 的列向量！）

A [q_{1}, q_{2}, \dots, q_{N}] = [q_{1}, q_{2}, \dots, q_{N}] [\begin{matrix} λ_{1} & \dots & 0 \\ ⋮ & ⋱ & ⋮ \\ 0 & \dots & λ_{N} \end{matrix}] A Q = Q Λ

$A[q_1,q_2,\cdots,q_N]=[q_1,q_2,\cdots,q_N]\left [\begin{matrix} \lambda_1 & \cdots & 0\\ \vdots &\ddots & \vdots \\0 & \cdots & \lambda_N \end{matrix} \right ]\\ AQ=Q\Lambda$
等式两边右乘

Q

$Q$ 的逆，得到

A

$A$ 的特征值分解：

A = Q Λ Q^{- 1}

$A=Q\Lambda Q^{-1}$
进一步，由于特征向量矩阵

Q

$Q$ 各列相互正交，所以

Q

$Q$ 是正交阵，正交阵的逆等于其转置:

A = Q Λ Q^{T}

$A=Q\Lambda Q^T$

A = [q_{1}, q_{2}, \dots, q_{N}] [\begin{matrix} λ_{1} & \dots & 0 \\ ⋮ & ⋱ & ⋮ \\ 0 & \dots & λ_{N} \end{matrix}] [q_{1}, q_{2}, \dots, q_{N}]^{T}

$A=[q_1,q_2,\cdots,q_N]\left [\begin{matrix} \lambda_1 & \cdots & 0\\ \vdots &\ddots & \vdots \\0 & \cdots & \lambda_N \end{matrix} \right ] [q_1,q_2,\cdots,q_N]^T$

特征值分解的几何意义

矩阵 $A$ 是一个既有旋转又有缩放的变换，用 $A$ 对向量 $x$ 进行矩阵变换 $Ax$ ，即对它进行旋转操作和缩放操作。整个过程在矩阵做EVD之后，可以看成 $Q\Lambda Q^Tx$ ，即 $x$ 依次经过 $Q^T$ ， $\Lambda$ 和 $Q$ 的变换，特别地，如果 $x$ 恰与矩阵 $A$ 的某个特征向量平行，那么它将不会发生旋转，只发生缩放。

$Q^Tx$ ：将 $x$ 由原始空间变换到由 $Q$ 各两两正交的特征向量构成的空间中
$\Lambda Q^Tx$ ：将变换后的 $x$ 在特征空间中缩放，轴 $q_i$ 的缩放因子正是对应的特征值 $\lambda_i$
$Q\Lambda Q^Tx$ ：将缩放过的 $x$ 变换回原始空间

矩阵变换举例

A = [\begin{matrix} 1 & - 1 \\ - 1 & 2 \end{matrix}] x = [0, 1]^{T}

$A=\left [ \begin{matrix}1 & -1 \\ -1 & 2 \end{matrix}\right ]\\x=[0,1]^T$

奇异值分解SVD

SVD定义

$M\times N$ 矩阵 $A$ 的SVD：

A = U \sum V^{T}

$A=U\sum V^T$

SVD推导

首先把 $A$ 变成 $N\times N$ 方阵 $A^TA$ ，于是就能做EVD：

(A^{T} A) v_{i} = λ_{i} v_{i} (A^{T} A) V = V Λ

$(A^TA)v_i=\lambda_i v_i\\(A^TA)V=V \Lambda$

然后把 $A$ 变成方阵 $M\times M$ ，于是就又能做EVD：

(A A^{T}) u_{i} = λ_{i} u_{i} (A A^{T}) U = U Λ

$(AA^T)u_i=\lambda_i u_i\\(AA^T)U=U \Lambda$

非方阵的秩最多为M和N较小值，两种情况下非零特征值是一样的，多余的特征值都是0。现在假设 $A$ 可以分解成 $A=U'\sum' V'^T$ 的形式，现在求出这三部分：

A^{T} = V^{'} \sum^{'} U^{' T} A^{T} A = V^{'} (\sum^{'})^{2} V^{' T} A A^{T} = U^{'} (\sum^{'})^{2} U^{' T}

$A^T=V'\sum' U'^T\\A^TA=V'(\sum')^2 V'^T\\AA^T=U'(\sum')^2 U'^T$
所以

V^{'} = V

$V'=V$ ，

U^{'} = U

$U'=U$ ，

\sum^{'} = \sqrt{Λ}

$\sum'=\sqrt{\Lambda}$ ，也就是说中间对角矩阵

\sum

$\sum$ 的元素可以这样求：

σ_{i} = \sqrt{λ_{i}}

$\sigma_i=\sqrt{\lambda_i}$

SVD性质

对角阵 $\sum$ 的奇异值从左上到右下按从大到小排序，一般来说少量几个奇异值（例如 $k$ 个）就占据了奇异值之和的绝大部分，因此可以只用这 $k$ 个奇异值和对应的左右特征向量表示原矩阵 $A$ ：

A = U_{M \times M} \sum_{M \times N} V_{N \times N}^{T} \approx U_{M \times k} \sum_{k \times k} V_{k \times N}^{T}

$A=U_{M\times M}\sum _{M\times N} V^T_{N\times N} \approx U_{M\times k}\sum _{k\times k} V^T_{k\times N}$

总结

SVD可以把任意形状的矩阵分解成 $A=U\sum V^T$ 的形式， $U$ 和 $V$ 都是有特征值分解得到的特征向量矩阵，它们都是正交阵， $\sum$ 可以由特征值开平方得到。只选择较大的奇异值就能很好地表示原矩阵。

EVD应用-PCA

初衷——最大方差投影

希望找到一个新的正交坐标系，将样本变换过去（投影过去），使得所有样本之间尽可能地分开（方差最大）。

样本集 $X$ 在坐标系 $W$ （W的每行就是一个标准正交基，即两两之间正交，且模为1）下的投影是 $W^TX$ （原因参见正交变换）
假设样本是去中心化的（均值为0），投影的方差为 $W^TXX^TW$
写出有约束优化问题

\begin{matrix} max & t r (W^{T} X X^{T} W) \\ s . t . & W^{T} W = I \end{matrix}

$\begin{matrix} \max &tr(W^TXX^TW)\\s.t. &W^TW=I \end{matrix}$

用拉格朗日乘子法求解：

L (W) = W^{T} X X^{T} W + λ (I - W^{T} W) \frac{\partial L (W)}{\partial W} = 2 X^{T} X W - 2 λ W (X^{T} X) W = λ W

$L(W)=W^TXX^TW+\lambda (I-W^TW)\\ \frac{\partial L(W)}{\partial W}=2X^TXW-2\lambda W\\ (X^TX)W=\lambda W$

如此可见，我们所需的新坐标系正是样本协方差 $X^TX$ （ $d\times d$ ）做特征值分解后的特征向量矩阵。总结一下PCA的流程：首先样本去中心化，然后计算样本协方差 $X^TX$ ，再对 $X^TX$ 做EVD，选取最大的部分特征值所对应的特征向量，构成投影矩阵 $W$ 。

SVD应用-LSA潜在语义分析

构造单词-文档矩阵

假设有 $D$ （Document）篇文章，每篇文章都是由很多个单词构成的结构（bag-of-words，单词的位置不重要，只关心数量），而单词来自于一个大小为 $W$ （Word）的字典，则构造 $W\times D$ 矩阵，第 $i$ 行第 $j$ 列表示单词 $W_i$ 在文档 $j$ 中出现的次数（或者tf-idf）。通常来说，该矩阵会相当地稀疏。
具体地，会先遍历所有文章进行分词，在这个过程中过滤掉停止词（例如a、the之类的）和标点等，然后进行词频计数等操作。

SVD

将单词-文档矩阵进行SVD，并且只选取部分足够大的奇异值（例如 $k$ 个），对应于不同的主题（语义）：

A_{W \times D} = U_{W \times k} S_{k \times k} V_{D \times k}^{T}

$A_{W\times D}=U_{W\times k}S_{k\times k}V^T_{D\times k}$

其中 $U_{W\times k}$ 描述了每个单词与不同主题之间的关系， $S_{k\times k}$ 描述了主题本身， $V_{D\times k}$ 描述了每篇文章与不同主题之间的关系。我们可以从 $U_{W\times k}$ 挖掘同义词，从 $V_{D\times k}$ 挖掘相似文档。那么到底为什么需要做SVD呢？是因为单纯地统计词频或tf-idf并不能描述单词之间或文本之间的关系。然而SVD有一个问题，就是每一个语义具体是什么不可解释，只知道他们是互相正交的。

从SVD到SVD++

SVD在电影推荐中的应用

问题提出

稀疏矩阵没法直接SVD，有很多数据是缺失的
SVD很慢，超过1000维的矩阵做SVD已经相当慢了

电影推荐

现有一个矩阵，行表示用户，列表示电影，矩阵中每个元素表示某个用户对某个电影的打分，显然这个矩阵是极其稀疏的（不是每个用户都看过所有电影的，大多只看过几部），有大量缺失值。现在的问题是，如何预测这些缺失值？即如何预测一个用户对他没看过的电影的评分？
首先，如果把U乘S看成一个矩阵，则SVD可以写成两个矩阵相乘：

A_{W \times D} = [U_{W \times k} S_{k \times k}] V_{D \times k}^{T}

$A_{W\times D}=[U_{W\times k}S_{k\times k}]V^T_{D\times k}$

那么电影评分矩阵也存在这种分解：

R_{U \times M} = P_{U \times k} Q_{k \times M}

$R_{U\times M}=P_{U\times k}Q_{k\times M}$

现在P和Q是未知的，如果能通过R中已知的评分训练P和Q，使得P和Q相乘的结果能最好地拟合R中未缺失值，则缺失值就可以通过P的一行乘上Q的一列得到：

{\hat{r}}_{u m} = p_{u}^{T} q_{m}

$\hat{r}_{um}=p_u^Tq_m$

P和Q的训练（基于梯度下降法）：Basic SVD

要拟合真实的已知评分 $r_um$ ，选取平方误差：

E = \frac{1}{2} \sum_{u} \sum_{m} (r_{u m} - {\hat{r}}_{u m})^{2} = \frac{1}{2} \sum_{u} \sum_{m} (r_{u m} - \sum_{j} p_{u j} q_{j m})^{2}

$E=\frac{1}{2} \sum_u \sum_m (r_{um}-\hat{r}_{um})^2=\frac{1}{2}\sum_u \sum_m (r_{um}-\sum_jp_{uj}q_{jm})^2$

计算梯度（当然只能代入R矩阵中 $r_{um}$ 有取值的计算），漂亮的对称结构：

\frac{\partial E}{\partial p_{u k}} = - (r_{u m} - {\hat{r}}_{u m}) q_{k m} = - e_{u m} q_{k m} \frac{\partial E}{\partial q_{k m}} = - (r_{u m} - {\hat{r}}_{u m}) p_{u k} = - e_{u m} p_{u k}

$\frac{\partial E}{\partial p_{uk}}=-(r_{um}-\hat{r}_{um})q_{km}=-e_{um}q_{km}\\ \frac{\partial E}{\partial q_{km}}=-(r_{um}-\hat{r}_{um})p_{uk}=-e_{um}p_{uk}$

接下来只需要将P和Q用随机数初始化，然后梯度下降迭代即可。

P和Q的训练：RSVD

引入正则化：

E = \frac{1}{2} \sum_{u, m} e_{u m}^{2} + \frac{1}{2} λ \sum_{u, k} p_{u k}^{2} + \frac{1}{2} λ \sum_{k, m} q_{k m}^{2}

$E=\frac{1}{2} \sum_{u,m} e_{um}^2+\frac{1}{2} \lambda \sum_{u,k} p_{uk}^2 + \frac{1}{2}\lambda \sum_{k,m} q_{km}^2$

计算梯度：

\frac{\partial E}{\partial p_{u k}} = - (r_{u m} - {\hat{r}}_{u m}) q_{k m} = - e_{u m} q_{k m} + λ p_{u k} \frac{\partial E}{\partial q_{k m}} = - (r_{u m} - {\hat{r}}_{u m}) p_{u k} = - e_{u m} p_{u k} + λ q_{k m}

$\frac{\partial E}{\partial p_{uk}}=-(r_{um}-\hat{r}_{um})q_{km}=-e_{um}q_{km}+\lambda p_{uk}\\ \frac{\partial E}{\partial q_{km}}=-(r_{um}-\hat{r}_{um})p_{uk}=-e_{um}p_{uk}+\lambda q_{km}$

有偏置的RSVD：RSVD 改

用户对电影的打分不仅取决于用户与电影之间的关系，还应该受到用户自身 $b_u$ 和电影自身性质 $b_m$ 的影响：

{\hat{r}}_{u m} = p_{u}^{T} q_{m} + b_{u} + b_{m} + μ

$\hat{r}_{um}=p_u^Tq_m+b_u+b_m+\mu$

其中 $\mu$ 是全局平均分，他描述了整个打分网站的整体打分水平。
引入正则化和惩罚：

E = \frac{1}{2} \sum_{u, m} e_{u m}^{2} + \frac{1}{2} λ \sum_{u, k} p_{u k}^{2} + \frac{1}{2} λ \sum_{k, m} q_{k m}^{2} + \frac{1}{2} λ \sum_{u} b_{u}^{2} + \frac{1}{2} λ \sum_{m} b_{m}^{2}

$E=\frac{1}{2} \sum_{u,m} e_{um}^2+\frac{1}{2} \lambda \sum_{u,k} p_{uk}^2 + \frac{1}{2}\lambda \sum_{k,m} q_{km}^2+\frac{1}{2} \lambda\sum_u b_u^2+\frac{1}{2} \lambda\sum_m b_m^2$

如此对于P和Q的导数不变，新增加的三个参数中，两个b是需要学习的，仍然用梯度下降迭代更新，初始值设0即可。

考虑邻域影响的SVD++

P和Q的训练：SVD++

在有偏置RSVD的基础上，还考虑了用户对电影的历史评分。ItemCF衡量用户 $u$ 对电影 $m$ 的兴趣：

{\hat{r}}_{u m}^{'} = \frac{1}{\sqrt{| N (u) |}} \sum_{j \in N (u)} w_{m j}

$\hat{r}_{um}'=\frac{1}{\sqrt{|N(u)|}}\sum_{j\in N(u)}w_{mj}$

这里 $N(u)$ 是用户 $u$ 喜欢的电影集合， $w_{mj}$ 是电影 $m$ 和电影 $j$ 的相似度（在ItemCF中，相似度通过统计所有用户观看的电影列表获得，但注意在SVD++中 $w$ 实际上是需要学习的参数），这个式子中求和项的意思是用户过去感兴趣的所有电影和电影 $m$ 的整体相似程度，左边分式用于归一化。
现在嫌矩阵 $W$ 太大，用SVD的思想它也能分解 $W=XY$ ，即用 $x_m^Ty_j$ 代替 $w_{mj}$ ， $x_m$ 和 $y_j$ 都是向量

{\hat{r}}_{u m}^{'} = \frac{1}{\sqrt{| N (u) |}} \sum_{j \in N (u)} x_{m}^{T} y_{j} = \frac{1}{\sqrt{| N (u) |}} x_{m}^{T} \sum_{j \in N (u)} y_{j}

$\hat{r}_{um}'=\frac{1}{\sqrt{|N(u)|}}\sum_{j\in N(u)}x_{m}^Ty_j=\frac{1}{\sqrt{|N(u)|}}x_{m}^T\sum_{j\in N(u)}y_j$

将这个兴趣加到RSVD上

{\hat{r}}_{u m} = b_{u} + b_{m} + μ + q_{m}^{T} p_{u} + \frac{1}{\sqrt{| N (u) |}} x_{m}^{T} \sum_{j \in N (u)} y_{j}

$\hat{r}_{um}=b_u+b_m+\mu+q_m^Tp_u+\frac{1}{\sqrt{|N(u)|}}x_{m}^T\sum_{j\in N(u)}y_j$

又嫌参数太多，让 $x=q$ ：

{\hat{r}}_{u m} = b_{u} + b_{m} + μ + q_{m}^{T} (p_{u} + \frac{1}{\sqrt{| N (u) |}} \sum_{j \in N (u)} y_{j})

$\hat{r}_{um}=b_u+b_m+\mu+q_m^T\left (p_u+\frac{1}{\sqrt{|N(u)|}}\sum_{j\in N(u)}y_j \right )$

如此一来，需要迭代学习的参数包括 $b_u$ ， $b_m$ ， $p_{uk}$ ， $q_{km}$ ， $y_j$ 。手撸梯度之后，梯度下降求解。

总结

PCA和SVD都能用来降维，只是PCA用的是特征值分解。
PCA需要对数据去中心化，可能使样本由稀疏变稠密，提高计算复杂度。
PCA只能获得矩阵一个方向的分解，SVD能获得两个方向的分解。
SVD实际上很慢，而且无法处理缺失值，所以采取矩阵分解梯度下降拟合未缺失值
梯度下降拟合可能会过拟合，因此采用RSVD
有偏置的RSVD是出于对用户和物品各自固有属性的考虑
SVD++是在有偏置的RSVD基础上，基于ItemCF考虑了用户历史喜好的SVD

参考资料

奇异值分解(SVD)原理详解及推导
 知乎-如何理解特征值
《推荐系统实践》

特征值分解与奇异值分解及其应用

SVD奇异值分解

正交矩阵

正交矩阵

正交变换举例

正交矩阵的性质

特征值分解

特征值分解

特征值分解的几何意义

矩阵变换举例

奇异值分解SVD

SVD定义

SVD推导

SVD性质

总结

EVD应用-PCA

初衷——最大方差投影

SVD应用-LSA潜在语义分析

构造单词-文档矩阵

SVD

从SVD到SVD++

SVD在电影推荐中的应用

问题提出

电影推荐

P和Q的训练（基于梯度下降法）：Basic SVD

P和Q的训练：RSVD

有偏置的RSVD：RSVD 改

考虑邻域影响的SVD++

P和Q的训练：SVD++

总结

参考资料

猜你喜欢