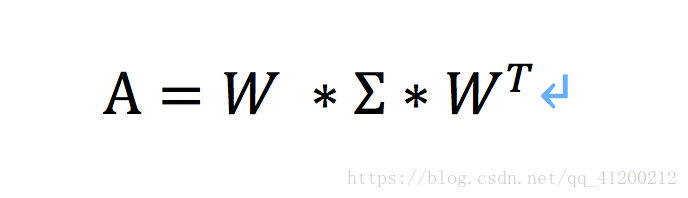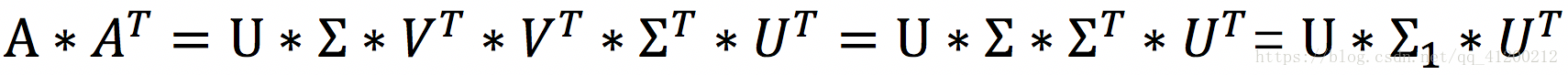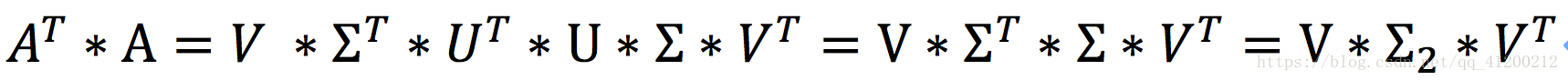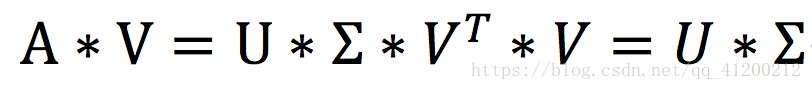特征值分解
学过线性代数的同学都知道，n阶方阵可以被特征分解为特征向量和特征值。特征向量可以组成特征矩阵，特征值组成对角矩阵，表示成下面的形式。如果是对称矩阵还可以分解成标准形。
奇异值分解
那么如果我们要处理的矩阵不是方阵它能不能被分解呢？当然可以。分解的方法被称为奇异值分解，即SVD。
奇异值分解在机器学习中的用途非常广泛，例如图像去噪，降维，另外还有推荐算法等。
假设有一个普通的矩阵A（m*n），我们可以将A表示成如下形式：
其中U、V为正交矩阵，E为m*n的对角阵。
证明上式：
图片来自张贤达老师的《矩阵分析与应用》
求解左奇异矩阵U和右奇异矩阵V
- 左奇异矩阵U：A*At得到一个m*m的方阵，于是我们对A*At进行特征值分解。即
，我们能得到m个特征值和对应的m个特征向量。m个向量组成特征向量矩阵U。
- 右奇异矩阵V：At*A得到一个n*n的方阵，于是我们对At*A进行特征值分解。即
，我们能得到n个特征值和对应的n个特征向量。n个向量组成特征向量矩阵V。
证明上方法能得到左右奇异矩阵
因为
求解奇异值
将矩阵A乘以右奇异矩阵V，如下
将对应的左奇异向量和右奇异向量代入上面式子，可以求出对应的奇异值lambda i。所有的lambda i组成中间的奇异值对角阵。