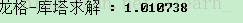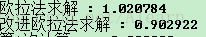【计算方法】数值积分求解微分方程

【常微分方程的数值解】

1.1微分方程

含有自变量、未知数及未知函数的导数或微分的方程称为微分方程。

• 在高等数学《微分方程》中，我知道了函数是客观事物的内部联系在数量方面的反映，利用函数关系可以对客观事物规律行进行研究。在实践过程中，我们找到一个函数关系往往是困难的，例如给定几个实验数据（x,y）,我们从某些数据能够知道他们存在一定的关系，但是不能用数学去表述它。这就可以用一个近似函数去逼近目标函数，可以使用插值与拟合来做。
• 有时候我们根据问题搜提供情况，我们可以知道要找的函数的导数的关系式，这种关系式，我们便称为微分方程，设法求未知函数，这就是解微分方程。
• 数值方法就算常微分方程基本出发点就是离散化，将[a,b]区间上一系列节点a<= x0 <= x1 <=……..<=xn <= b的函数值y0,y1,y2,yn计算出来。相邻的两个节点的间距h=xi+1 - xi，h是步长。可以采用变步长和定步长两种做法。单步长的做法就是龙格库塔的做法。
  下面代码就是以欧拉法和改进的欧拉法，以及四阶龙格-库塔公式求解。
  

#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#include<string.h>
#define pi 3.1415926
/***********************************
* 用欧拉法和四节Runge-kutta法求解常微分方程
*  y' = -y + 2*cos(x) 
*  y(0) = -1;
***********************************/
//斜率
double f(double x, double y) {
     double k = 2 * cos(x) - y;
     return k;
}
//欧拉法求解
double EuLer(double x0, double xn, double y0, double h) 
{
     int count = 1;
     int N = (xn - x0) / h;
     double x = x0;
     double y = y0; 
     while(count <= N) {

      y +=  f(x,y) * h;
      x += h;
      printf("第%d次计算 x = %lf  y = %lf\n", count++, x , y);
     }
     return y;
}

/******************************************************
*改进的欧拉法求解原理
* 利用三点 欧拉法 + 梯形公式
*  y' = y + h *f(x,y);
*  y' = y + h *(f(x,y) + f(x', y')) / 2;
*******************************************************/
double Euler2(double x0, double xn, double y0, double h) 
{

     int count = 1; 
     int N = (xn - x0) / h;
     double x = x0;
     double x1;
     double y = y0;
     double yp;
     double yc;
     while (count <= N) {
      x1 = x + h;
      yp = y + h * f(x,y);
      yc = y + h * (f(x, y) + f(x1, yp));
      y = (yp + yc) / 2;
      x = x1;
      count++;
     }
     return y;
}
//龙格-库塔法求解
double runge_Kutta(double x0, double xn, double y0, double h) 
{
     int count = 1;
     int N = (xn - x0) / h;
     double x = x0;
     double y = y0;
     double x1;
     double k1;
     double k2;
     double k3;
     double k4;
     while (count <= N) {
          x1 = x + h;
          k1 = f(x, y);
          k2 = f(x + h /2, y + h * k1 / 2);
          k3 = f(x + h / 2, y + h * k2 / 2);
          k4 = f(x + h, y + h * k3);
          y += h * (k1 + 2 * k2 + 2 * k3 + k4) / 6;
          printf("第%d次计算 x = %lf  y = %lf\n", count++, x , y);
          x = x1;

     }
     return y;
}
int main() 
{
     double x0 = 0;
     double xn = pi / 2;
     double y0 = 1;
     double h = 0.02;
     double ans = EuLer(x0, xn, y0, h);
     printf("欧拉法求解 : %lf\n",ans);

     ans = Euler2(x0, xn, y0, h);
     printf("改进欧拉法求解 : %lf\n",ans);

     ans = runge_Kutta(x0, xn, y0, h);
     printf("龙格-库塔求解 : %lf\n",ans);

     return 0;
}

运行结果