SLAM卡尔曼滤波&&非线性优化

SLAM卡尔曼滤波&&非线性优化

高斯分布（正态分布）是一个常见的连续概率分布。正态分布的数学期望值或期望值$\mu$等于位置参数，决定了分布的位置；其方差${\sigma }^2$ 的开平方或标准差$\sigma$ 等于尺度参数，决定了分布的幅度。

1.高斯分布

一个随机变量$x$服从高斯分布$N$，那么它的概率密度函数为：
$$p(x)=\frac{1}{\sigma \sqrt{2\pi }}exp(-\frac{(x-\mu {)}^2}{2{\sigma }^2})$$
它的高维形式为：
$$P(x)=\frac{1}{\sqrt{(2\pi {)}^{N}det(\Sigma )}}exp(-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu ))$$

2.高斯分布的运算

2.1 线性运算

设两个独立的高斯分布：
$$x\sim N({\mu }_x,{\Sigma }_{xx}),y\sim N({\mu }_y,{\Sigma }_{yy})$$
那么他们的和仍然是高斯分布：
$$x+y\sim N({\mu }_x+{\mu }_y,{\Sigma }_{xx}+{\Sigma }_{yy})$$
如果以常数$a$乘以$x$，那么$ax$满足：
$$ax\sim N({\mu }_{a}x,a^2{\Sigma }_{xx})$$
如果取$y=Ax$,那么$y$满足：
$$y\sim N({\mu }_{A}x,A^2{\Sigma }_{xx})$$

2.2乘积

设两个高斯分布的乘积满足$p(xy)=N(\mu ,\Sigma )$,那么：
$$\begin{gathered} {\Sigma }^{-1}={\Sigma }_{xx}^{-1}+{\Sigma }_{yy}^{-1} \\ {\Sigma }_{\mu }={\Sigma }_{xx}^{-1}{\mu }_x+{\Sigma }_{yy}^{-1}{\mu }_y \end{gathered}$$

2.2复合运算

同时考虑到$x$和$y$，当他们不独立时，其复合分布为：
$$p(x,y)=N\left(\left[\begin{array}{c}{\mu }_x\\ {\mu }_y\end{array}\right],\left[\begin{array}{cc}{\Sigma }_{xx}& {\Sigma }_{xy}\\ {\Sigma }_{yx}& {\Sigma }_{yy}\end{array}\right]\right)$$
其中${\Sigma }_{yx}$和${\Sigma }_{yx}$为两个变量的协方差，满足：
$$Cov(X,Y)=E[(X-E(X))(Y-E(Y))]=E[XY]-E[X]E[Y]$$
协方差为正，则说明这两个变量呈正相关，为零则不相关，为负则为负相关。
由条件分布（贝叶斯法则）展开式$p(x,y)=p(x|y)p(y)$可以推出，条件概率$p(x|y)$满足：
$$p(x|y)=N({\mu }_x+{\Sigma }_{xx}{\Sigma }_{yy}^{-1}(y-{\mu }_y),{\Sigma }_{xx}-{\Sigma }_{xy}{\Sigma }_{yy}^{-1}{\Sigma }_{yx})$$

---

舒尔补

现在来推导如何得出该结论：
舒尔补理论：把矩阵分解成上三角矩阵、对角阵、下三角矩阵乘积的形式，方便运算，即：
$$\begin{gathered} \left[\begin{array}{cc}A& B\\ C& D\end{array}\right] \\ =\left[\begin{array}{cc}I& B{D}^{-1}\\ 0& I\end{array}\right]\left[\begin{array}{cc}\Delta D& 0\\ 0& D\end{array}\right]\left[\begin{array}{cc}I& 0\\ D^{-1}C& I\end{array}\right] \end{gathered}$$
其中$\Delta D=A-B{D}^{-1}C$称为矩阵$D$的舒尔补。
同样地：
$$\begin{gathered} {\left[\begin{array}{cc}A& B\\ C& D\end{array}\right]}^{-1} \\ =\left[\begin{array}{cc}I& 0\\ -D^{-1}C& I\end{array}\right]\left[\begin{array}{cc}\Delta D^{-1}& 0\\ 0& D^{-1}\end{array}\right]\left[\begin{array}{cc}I& -B{D}^{-1}\\ 0& I\end{array}\right] \end{gathered}$$

---

具体推导过程（了解）

由于$p(x|y)=p(x,y)/p(y)$,根据其指数部分展开形式可以得到：
$$\begin{gathered} {\left(\left[\begin{array}{c}x\\ y\end{array}\right]-\left[\begin{array}{c}{\mu }_x\\ {\mu }_y\end{array}\right]\right)}^T{\left[\begin{array}{cc}{\Sigma }_{xx}& {\Sigma }_{xy}\\ {\Sigma }_{yx}& {\Sigma }_{yy}\end{array}\right]}^T\left(\left[\begin{array}{c}x\\ y\end{array}\right]-\left[\begin{array}{c}{\mu }_x\\ {\mu }_y\end{array}\right]\right) \\ ={\left(\left[\begin{array}{c}x\\ y\end{array}\right]-\left[\begin{array}{c}{\mu }_x\\ {\mu }_y\end{array}\right]\right)}^T\left[\begin{array}{cc}1& 0\\ -{\Sigma }_{yy}^{-1}{\Sigma }_{yx}& 1\end{array}\right]\left[\begin{array}{cc}({\Sigma }_{xx}-{\Sigma }_{xy}{\Sigma }_{yy}^{-1}{\Sigma }_{yx}{)}^{-1}& 0\\ 0& {\Sigma }_{yy}^{-1}\end{array}\right]\left[\begin{array}{cc}1& -{\Sigma }_{xy}{\Sigma }_{yy}^{-1}\\ 0& 1\end{array}\right]\left(\left[\begin{array}{c}x\\ y\end{array}\right]-\left[\begin{array}{c}{\mu }_x\\ {\mu }_y\end{array}\right]\right) \\ ={\left(x-{\mu }_x-{\Sigma }_{xx}{\Sigma }_{yy}^{-1}(y-{\mu }_y)\right)}^T({\Sigma }_{xx}-{\Sigma }_{xy}{\Sigma }_{yy}^{-1}{\Sigma }_{yx}{)}^T{\left(x-{\mu }_x-{\Sigma }_{xx}{\Sigma }_{yy}^{-1}(y-{\mu }_y)\right)}^T+(y-{\mu }_y{)}^T{\Sigma }_{yy}^{-1}(y-{\mu }_y) \end{gathered}$$
由于$p(y)$的指数部分为：
$$(y-{\mu }_y{)}^T{\Sigma }_{yy}^{-1}(y-{\mu }_y)$$
因此，
$$p(x|y)=p(x,y)/p(y)=N({\mu }_x+{\Sigma }_{xx}{\Sigma }_{yy}^{-1}(y-{\mu }_y),{\Sigma }_{xx}-{\Sigma }_{xy}{\Sigma }_{yy}^{-1}{\Sigma }_{yx})$$

---

3.复合运算例子

考虑到随机变量$x\sim N({\mu }_x,{\Sigma }_{xx})$，另一变量$y$满足：
$$y=Ax+b+w$$
其中$A，b$为线性变量的系数矩阵和偏移量，$w$为噪声项，为零均值的高斯分布：$w\sim N(0,R)$.因此：
$$\begin{gathered} E(y)=E(Ax+b+w)=AE(x)+b+E(w)=A{\mu }_x+b \\ Cov(y)=E[(x-E[x])(x-E(x))]+Cov(w)=AE[(x-{\mu }_x)(x-{\mu }_x{)}^T]A^T+R=A{\Sigma }_{xx}{A}^T+R \end{gathered}$$
$$p(y)=N(A{\mu }_x+b,A{\Sigma }_{xx}{A}^T+R)$$

4.SLAM问题的数学表述

通常，机器人或者无人车在运动过程中会携带一个测量自身运动的传感器（IMU,轮速里程计等），通过积分运算可以抽象出一个关于本体感知的数学模型：
$$x_k=f(x_{k-1},u_k,w_k)$$
这里的$u_k$是运动传感器的读数（有时候也称为输入），$w_k$为噪声，该方程称为运动方程，目前没有给出具体的运动意义，是因为运动传感器可以是选择的，根据不同的运动传感器可以列出不同的方程，或者是他们的组合，即多传感器融合。
同样的，在SLAM中还有一个环境感知传感器（激光雷达、相机、红外设备）的观测部分，环境感知所对应的方程为观测方程，当机器人或者无人车在$x_k$的位置上观测到某个路标点$y_j$，此时产生了一个观测数据z_{k,j}，同样的抽象出其数学模型为：
$$z_{k,j}=h(y_j,x_k,v_{k,j})$$
其中，$v_{k,j}$为观测噪声，同样观测方程根据环境传感器的不同而有不同的形式。
因此SLAM问题可以总结出两个基本的方程：
$$\{\begin{array}{lr}{x}_k=f(x_{k-1},u_k,w_k)& \\ z_{k,j}=h(y_j,x_k,v_{k,j})& \end{array}$$
从上述方程中可以看出：
1.观测方程中，只有在位置$x_k$看到了$y_j$时才会产生观测数据，否则就没有。然而在实际过程中，一个位置通常可以看到一小部分路标，同时无论是相机还是激光雷达观察特征时，特征点数量较多，所以实际过程中观测方程会远远大于运动方程数量。
2.运动方程中，实际过程中，如果做纯视觉SLAM或者纯激光SLAM，往往会缺少运动方程；在这种时候的处理方式通常假设为车辆匀速运动或者不动或者匀加速运动等。
3.位姿$x$（定位）和路标$y$（建图）看成服从某种概率分布的随机变量，而不是单独的一个数。由于两者都是待估计的量，改变一下记号，令$x_k$为$k$时刻的所有未知量，同时包含了当前时刻的车辆位姿（假设已经完成传感器与车体的标定）与m个路标点，则：
x k ≜ { x k , y 1 , . . . . . . , y m } x_k\triangleq \{x_k,y_1,......,y_m\} xk​≜{ xk​,y1​,......,ym​}
同样的把$k$时刻所有的观测量都记为$z_k$，于是：
$$\{\begin{array}{lr}{x}_k=f(x_{k-1},u_k)+w_k& \\ z_k=h(x_k)+v_{k,j}& \end{array}$$
直接给出待估计的后验概率密度为：
$$P(x_k|x_0,u_{1:k},z_{1:k})$$
其中：
$x_0$表示状态的初识值；$u_{1:k}$表示$1$到$k$运动传感器的输入；$z_{1:k}$表示的$0$到$k$时刻所有的观测,该问题表示的是：**根据所有历史数据(输入、观测、初始状态)得出最终的融合结果，即滤波问题。**用图表示为：

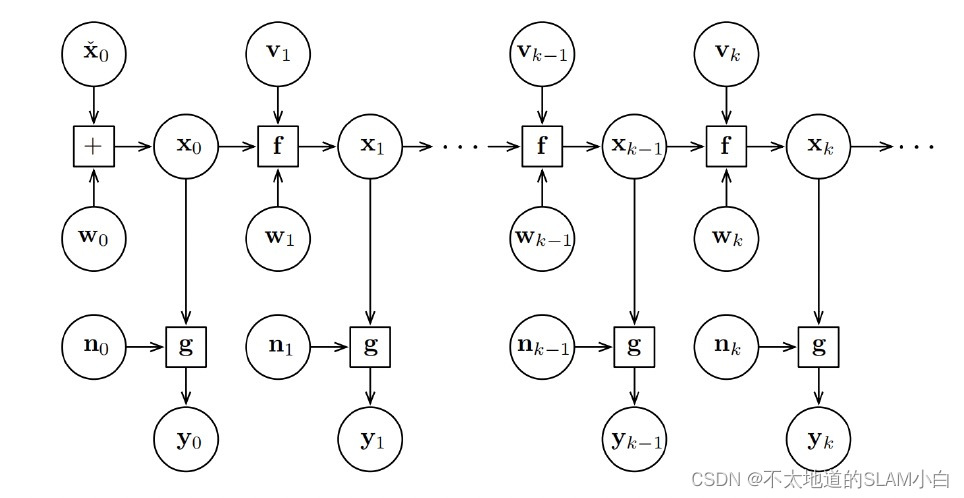
根据Bayes 法则，将$z_k$和$x_k$交换位置：
$$P(x_k|x_0,u_{1:k},z_{1:k})\propto P(z_k|x_k)P(x_k|x_0,u_{1:k},z_{1:k-1})$$
这里注意：第一项称为似然，第二项称为先验。在不同的分法中，先验部分其实有通过运动预测得到的，称为预测部分，也有基于过去的所有状态得到部分称为先验，如下，按照$x_k-1$时刻为条件概率展开：
$$P(x_k|x_0,u_{1:k},z_{1:k-1})=\int P(x_k|x_{k-1},x_0,u_{1:k},z_{1:k-1})P(x_{k-1}|x_0,u_{1:k},z_{1:k-1})d{x}_{k-1}$$
对于该公式，这里称为（A）公式，得出以下结论与假设：
1.如果我们考虑更久之前的状态，也可以继续对此式进行展开。
2.如果只关心只关心$k$时刻和$k-1$时刻，可以假设为一阶马尔可夫性：$k$时刻的状态只与$k-1$时刻状态无关，而与再之前的状态无关，得到滤波的方法，如扩展卡尔曼滤波器（EKF）：以某时刻的状态估计，推导到下一时刻。
3.如果考虑$k$时刻状态与之前所有状态的联系，得到非线性优化为主体的优化框架。

5.卡尔曼滤波（KF）

对（A）公式进行马尔可夫假设，当前时刻只与上一时刻有关，预测部分为：
$$P(x_k|x_{k-1},x_0,u_{1:k},z_{1:k-1})=P(x_k|x_{k-1},u_k)$$
先验部分可以简化为：
$$P(x_{k-1}|x_0,u_{1:k},z_{1:k-1})=P(x_{k-1}|x_0,u_{1:k-1},z_{1:k-1})$$
从图上可以看出输入量$u_k$与$k-1$时刻无关。上面的两个方程：以$k-1$时刻的状态估计，推导到$k$时刻。
假设：
1.这里的状态量服从高斯分布，那只需考虑维护状态量的均值和协方差即可。
2.所有的状态和噪声均满足高斯分布。
线性高斯系统可以使用运动方程和观测方程来表示：
$$\{\begin{array}{lr}{x}_k=A_k{x}_{k-1}+u_k+w_k& \\ z_k=C_k{x}_k+v_k& \end{array}$$
噪声服从零均值高斯分布，则：
$$w_k\sim N(0,\mathbf{R}),v_k\sim N(0，\mathbf{Q})$$
记$\hat{x}$为后验，$\overline{x}$为先验分布，假设已知$k-1$时刻的后验状态估计：${\hat{x}}_{k-1}$和此时的协方差${\hat{\mathbf{P}}}_{k-1}$。此时的目的比较明确：根据$k-1$时刻的后验状态估计，以及输入和观测数据确定$k$时刻的后验分布。
1.预测部分
根据运动方程和高斯分布确定为：
$$P(x_k|x_{k-1},x_0,u_{1:k},z_{1:k-1})=N({\mathbf{A}}_k{\hat{x}}_{k-1}+u_k,{\mathbf{A}}_k{\hat{\mathbf{P}}}_{k-1}{\mathbf{A}}_k^T+\mathbf{R})$$
记：
$$\overline{x}={\mathbf{A}}_k{\hat{x}}_{k-1}+u_k,\overline{\mathbf{P}}={\mathbf{A}}_k{\hat{\mathbf{P}}}_{k-1}{\mathbf{A}}_k^T+\mathbf{R}$$
2.观测方程
观测方程可以计算在某个状态下，应该观测数据，根据观测方程和高斯分布确定为：
$$P(z_k|x_k)=N(C_k{x}_k,Q)$$
设结果为$x_k\sim N({\hat{x}}_k,{\hat{\mathbf{P}}}_k)$,根据公式：
$$P(x_k|x_0,u_{1:k},z_{1:k})\propto P(z_k|x_k)P(x_k|x_0,u_{1:k},z_{1:k-1})$$
可以得到前面推导很熟悉的一个公式：
$$N({\hat{x}}_k,{\hat{\mathbf{P}}}_k)=N({\overline{x}}_k,{\overline{\mathbf{P}}}_k)\cdot N({\mathbf{C}}_k{x}_k,\mathbf{Q})=N\left(\left[\begin{array}{c}{\mu }_x\\ {\mu }_y\end{array}\right],\left[\begin{array}{cc}{\Sigma }_{xx}& {\Sigma }_{xy}\\ {\Sigma }_{yx}& {\Sigma }_{yy}\end{array}\right]\right)$$
直接用结论：
$$N({\hat{x}}_k,{\hat{\mathbf{P}}}_k)=N({\mu }_x+{\Sigma }_{xy}{\Sigma }_{yy}^{-1}(y-{\mu }_y),{\Sigma }_{xx}-{\Sigma }_{xy}{\Sigma }_{yy}^{-1}{\Sigma }_{yx})$$
这里可以直接看到：
$$\begin{gathered} {\overline{\mathbf{P}}}_k={\Sigma }_{xx} \\ {\Sigma }_{yy}=\Sigma (C_k{x}_k)+\Sigma (n)=E[(C_k{x}_k-u_x)(C_k{x}_k-u_x{)}^T]+\mathbf{Q}=C_k{\overline{\mathbf{P}}}_k{C}_k^T+\mathbf{Q} \end{gathered}$$
可以推导出
$$\begin{gathered} {\Sigma }_{xy}=E[(x-u_x)(z_k-u_z{)}^T] \\ =E[(x-u_x)(C_k{x}_k-C_k{u}_x+n{)}^T)] \\ =E[(x-u_x)(C_k{x}_k-C_k{u}_x{)}^T+(x-u_x)n^T] \\ ={\Sigma }_{xx}{C}_k^T \\ ={\overline{\mathbf{P}}}_k{C}_k^T \\ {\Sigma }_{yx}={\Sigma }_{xy}^T=C_k{\overline{\mathbf{P}}}_k \end{gathered}$$
定义：
$$\mathbf{K}={\Sigma }_{xy}{\Sigma }_{yy}^{-1}={\overline{\mathbf{P}}}_k{C}_k^T(C_k{\overline{\mathbf{P}}}_k{C}_k^T+\mathbf{Q}{)}^{-1}$$
则有
$$\begin{gathered} {\hat{\mathbf{P}}}_k={\overline{\mathbf{P}}}_k-\mathbf{K}{C}_k{\overline{\mathbf{P}}}_k=(\mathbf{I}-\mathbf{K}{C}_k){\overline{\mathbf{P}}}_k \\ {\hat{x}}_k={\overline{x}}_k+\mathbf{K}(z_k-C_k\overline{x}) \end{gathered}$$
整理一下，五个方程为：

1.预测： $$\overline{x}={\mathbf{A}}_k{\hat{x}}^{k-1}+u_k,\overline{{\mathbf{P}}_{\mathbf{k}}}={\mathbf{A}}_k{\hat{\mathbf{P}}}_{k-1}{\mathbf{A}}_k^T+\mathbf{R}$$
2.更新：先计算$\mathbf{K}$,又称为卡尔曼增益：
$$\mathbf{K}={\overline{\mathbf{P}}}_k{C}_k^T(C_k{\overline{\mathbf{P}}}_k{C}_k^T+\mathbf{Q}{)}^{-1}$$
然后计算后验概率分布： $$\begin{gathered} {\hat{\mathbf{P}}}_k=(\mathbf{I}-\mathbf{K}{C}_k){\overline{\mathbf{P}}}_k \\ {\hat{x}}_k={\overline{x}}_k+\mathbf{K}(z_k-C_k\overline{x}) \end{gathered}$$

至此，我们推导了经典的卡尔曼滤波器的整个过程。事实上卡尔曼滤波器有若干种推导方式，而我们使用的是从概率角度出发的最大后验概率估计的形式。我们看到，在线性高斯系统中，卡尔曼滤波器构成了该系统中的最大后验概率估计。而且，由于高斯分布经
过线性变换后仍服从高斯分布，所以整个过程中我们没有进行任何的近似。可以说，卡尔曼滤波器构成了线性系统的最优无偏估计。

6.扩展卡尔曼滤波（EKF）

卡尔曼滤波器通常适用于线性系统，但是在SLAM中，运动方程和观测方程通常为非线性函数。无论视觉SLAM模型还是激光SLAM，使用李代数表示位姿，更不可能是一个线性系统。一个高斯分布，经过非线性变换后，往往不再是高斯分布，所以在非线性系统中，需要进行近似处理，将一个非高斯分布近似成一个高斯分布。
通常把卡尔曼滤波器的结果拓展到非线性系统中来，称为扩展卡尔曼滤波器（Extended Kalman Filter，EKF），通常的做法是，在某个点附近考虑运动方程以及观测方程的一阶泰勒展开，只保留一阶项，即线性部分，然后按照线性系统进行推导。非线性化的运动方程和观测方程为：
运动方程：
$$x_k=f(x_{k-1},u_k,w_k)$$
观测方程为：
$$z_k=h(x_k,n_k)$$

令$k-1$时刻点均值与协方差矩阵为为${\hat{\mathbf{x}}}_{k-1}$,${\hat{\mathbf{P}}}_{k-1}$。在$k$时刻，把运动方程和观测方程，在${\hat{\mathbf{x}}}_{k-1}$,${\hat{\mathbf{P}}}_{k-1}$处进行线性化（相当于一阶泰勒展开）：
$${x_k\approx f({\hat{x}}_{k-1},u_k,w_k)+\frac{\partial f}{\partial x_{k-1}}|}_{{\hat{x}}_{k-1}}(x_{k-1}-{\hat{x}}_{k-1})+{\frac{\partial f}{\partial w_k}|}_{{\hat{x}}_{k-1}}{w}_k$$
记这里的偏导数为：
$${\mathbf{F}=\frac{\partial f}{\partial x_{k-1}}|}_{{\hat{x}}_{k-1}}$$
$${\mathbf{B}}_{k-1}={\frac{\partial f}{\partial w_k}|}_{{\hat{x}}_{k-1}}$$
对于观测方程，同样地有：
$${z_k\approx h({\overline{x}}_k)+\frac{\partial h}{\partial x_k}|}_{{\overline{x}}_k}(x_k-{\overline{x}}_k)+{\frac{\partial h}{\partial n_k}|}_{{\overline{x}}_k}{n}_k$$
记:
$${\mathbf{H}=\frac{\partial h}{\partial x_k}|}_{{\hat{x}}_k}$$
$$C_k={\frac{\partial h}{\partial n_k}|}_{{\overline{x}}_k}$$
展开线性化结果方程为：
$$E[x_k]=f({\hat{x}}_{k-1},u_k,0)+{\mathbf{F}}_{k-1}(x_{k-1}-{\hat{x}}_{k-1})+E[{\mathbf{B}}_{k-1}{w}_k]$$
这里$w_k$和$n_k$服从零均值分布即：
$$w_k\sim N(0,\mathbf{R}),n_k\sim N(0，\mathbf{Q})$$
因此$E[{\mathbf{B}}_{k-1}{w}_k]=0$,
这里$E(x_{k-1}]={\hat{x}}_{k-1}$$E({\hat{x}}_{k-1})={\hat{x}}_{k-1}$
结果为：
$$E[x_k]=f({\hat{x}}_{k-1},u_k,0)$$
协方差矩阵为：
$$\begin{array}{rl}Cov[x_k]& =E[(x_{k-1}-E[x_{k-1}])(x_{k-1}-E[x_{k-1}]{)}^T]+Cov[{\mathbf{B}}_{k-1}{w}_k]\\ & =\mathbf{F}{\hat{\mathbf{P}}}_{k-1}{\mathbf{F}}^T+{\mathbf{B}}_{k-1}{\mathbf{R}}_k{\mathbf{B}}_{k-1}^T\end{array}$$
*这里的推导根据高斯分布协方差的传递性：
$$\begin{gathered} E(y)=E(Ax+b+w)=AE(x)+b+E(w)=A{\mu }_x+b \\ Cov(y)=E[(x-E[x])(x-E(x))]+Cov(w)=AE[(x-{\mu }_x)(x-{\mu }_x{)}^T]A^T+R=A{\Sigma }_{xx}{A}^T+R \end{gathered}$$
$$Cov[{\mathbf{B}}_{k-1}{w}_k]={\mathbf{B}}_{k-1}\mathbf{C}ov[w_k]{\mathbf{B}}_{k-1}^T$$
综合可以得到
$$p(x_k|x_0,u_{1:k},z_{0:k-1})=N(f({\hat{x}}_{k-1},u_k,0),\mathbf{F}{\hat{\mathbf{P}}}_{k-1}{\mathbf{F}}^T+{\mathbf{B}}_{k-1}{\mathbf{R}}_k{\mathbf{B}}_{k-1}^T)$$
与卡尔曼滤波相似，这里有：
$${\overline{x}}_k=f({\hat{x}}_{k-1},u_k,0),{\overline{\mathbf{P}}}_k=\mathbf{F}{\hat{\mathbf{P}}}_{k-1}{\mathbf{F}}^T+{\mathbf{B}}_{k-1}{\mathbf{R}}_k{\mathbf{B}}_{k-1}^T$$
同样地，在观测方程中：
$$\begin{gathered} E[z_k]=E[h({\overline{x}}_k)+\mathbf{H}(x_k-{\overline{x}}_k)+{\mathbf{C}}_k{n}_k]=h({\overline{x}}_k)+\mathbf{H}(x_k-{\overline{x}}_k) \\ Cov[z_k]=E[({\overline{x}}_k-E[{\overline{x}}_k])({\overline{x}}_k-E[{\overline{x}}_k]{)}^T]+Cov[{\mathbf{C}}_k{n}_k] \\ ={\mathbf{C}}_{k}E[n_k]{\mathbf{C}}_k^T={\mathbf{C}}_k\mathbf{Q}{\mathbf{C}}_k^T \end{gathered}$$
观测为
$$p(z_k|x_k)=N(h({\overline{x}}_k)+\mathbf{H}(x_k-{\overline{x}}_k),{\mathbf{C}}_k\mathbf{Q}{\mathbf{C}}_k^T)$$
推导EKF同样为：
$$N({\hat{x}}_k,{\hat{\mathbf{P}}}_k)=N({\overline{x}}_k,{\overline{\mathbf{P}}}_k)\cdot N(h({\overline{x}}_k)+\mathbf{H}(x_k-x_{k-1}),{\mathbf{C}}_k\mathbf{Q}{\mathbf{C}}_k^T)=N\left(\left[\begin{array}{c}{\mu }_x\\ {\mu }_y\end{array}\right],\left[\begin{array}{cc}{\Sigma }_{xx}& {\Sigma }_{xy}\\ {\Sigma }_{yx}& {\Sigma }_{yy}\end{array}\right]\right)$$
同样直接用结论：
直接用结论：
$$N({\hat{x}}_k,{\hat{\mathbf{P}}}_k)=N({\mu }_x+{\Sigma }_{xy}{\Sigma }_{yy}^{-1}(y-{\mu }_y),{\Sigma }_{xx}-{\Sigma }_{xy}{\Sigma }_{yy}^{-1}{\Sigma }_{yx})$$
这里可以直接看到：
$$\begin{gathered} {\overline{\mathbf{P}}}_k={\Sigma }_{xx} \\ {\Sigma }_{yy}=\Sigma (h({\overline{x}}_k))+\Sigma (H_k(x_k-{\overline{x}}_k))+\Sigma ({\mathbf{C}}_k{n}_k)=0+\mathbf{H}E[(x_{k-1}-E[x_{k-1}])(x_{k-1}-E[x_{k-1}]{)}^T]{\mathbf{H}}^T+{\mathbf{C}}_k\mathbf{Q}{\mathbf{C}}_k^T=\mathbf{H}{\overline{\mathbf{P}}}_k{\mathbf{H}}^T+{\mathbf{C}}_k\mathbf{Q}{\mathbf{C}}_k^T \end{gathered}$$
可以推导出
$$\begin{gathered} {\Sigma }_{xy}=E[(x-u_x)(z_k-u_z{)}^T] \\ =E[(x-u_x)(h({\overline{x}}_k)+\mathbf{H}(x_k-{\overline{x}}_k)+\mathbf{C}{n}_k-h({\overline{x}}_k)] \\ =E[(x-u_x)({\mathbf{H}}_k{x}_k-{\mathbf{H}}_k{u}_x{)}^T+(x-u_x)n^T] \\ ={\Sigma }_{xx}{\mathbf{H}}_k^T \\ ={\overline{\mathbf{P}}}_k{\mathbf{H}}_k^T \\ {\Sigma }_{yx}={\Sigma }_{xy}^T={\mathbf{H}}_k{\overline{\mathbf{P}}}_k \end{gathered}$$
定义卡尔曼增益：
$${\mathbf{K}}_k={\Sigma }_{xy}{\Sigma }_{yy}^{-1}={\overline{\mathbf{P}}}_k{H}_k^T(H_k{\overline{\mathbf{P}}}_k{H}_k^T+{\mathbf{C}}_k\mathbf{Q}{\mathbf{C}}_k^T{)}^{-1}$$
在卡尔曼增益的基础上：
$${\hat{x}}_k={\overline{x}}_k+{\mathbf{K}}_k(z_k-h({\overline{x}}_k))$$
$${\hat{\mathbf{P}}}_k={\overline{\mathbf{P}}}_k-{\mathbf{K}}_k{\mathbf{H}}_k{\overline{\mathbf{P}}}_k=(\mathbf{I}-{\mathbf{K}}_k{\mathbf{H}}_k){\overline{\mathbf{P}}}_k$$
综上，得到EKF的经典五个公式为：

1.预测：
$${\overline{x}}_k=f({\hat{x}}_{k-1},u_k,0),{\overline{\mathbf{P}}}_k=\mathbf{F}{\hat{\mathbf{P}}}_{k-1}{\mathbf{F}}^T+{\mathbf{B}}_{k-1}{\mathbf{R}}_k{\mathbf{B}}_{k-1}^T$$
2.更新：先计算$\mathbf{K}$,又称为卡尔曼增益：
$${\mathbf{K}}_k={\Sigma }_{xy}{\Sigma }_{yy}^{-1}={\overline{\mathbf{P}}}_k{H}_k^T(H_k{\overline{\mathbf{P}}}_k{H}_k^T+{\mathbf{C}}_k\mathbf{Q}{\mathbf{C}}_k^T{)}^{-1}$$
然后计算后验概率分布：
$$\begin{gathered} {\hat{\mathbf{P}}}_k={\overline{\mathbf{P}}}_k-{\mathbf{K}}_k{\mathbf{H}}_k{\overline{\mathbf{P}}}_k=(\mathbf{I}-{\mathbf{K}}_k{\mathbf{H}}_k){\overline{\mathbf{P}}}_k \\ {\hat{x}}_k={\overline{x}}_k+{\mathbf{K}}_k(z_k-h({\overline{x}}_k)) \end{gathered}$$

至此，扩展卡尔曼滤波（EKF）已经全部推导结束，EKF以形式简洁、应用广泛著称，在早期SLAM中占据了很长一段时间的主导地位，但是EKF有一些局限性：

---

1.滤波器在一定程度上假设了马尔科夫性：$k$时刻的状态只与$k-1$时刻相关，而与$k-1$之前的状态和观测都无关（或者和前几个有限时间的状态相关)。这一假设导致激光/视觉里程计只考虑相邻两帧关系，遇到回环的情况，难以处理，这就需要非线性优化的方法将所有的历史数据放在一起进行优化，但是缺点是使得计算量上升，消耗更多的计算资源。
2.EKF滤波器仅在${\hat{x}}_{k-1}$处做了一次线性化，然后就直接根据这次线性化结果，计算后验概率。该方法认为该点处的线性化近似，在后验概率仍然是有效的。而实际上，当我们离开工作点较远的时候，一阶泰勒展开并不一定能够近似整个函数，这取决于运动模型和观测模型的非线性情况。如果它们有强烈的非线性，那线性近似就只在很小范围内成立，不能认为在很远的地方仍能用线性来近似。这就是EKF的非线性误差，是它的主要问题所在。
3.从程序实现上来说，EKF 需要存储状态量的均值和方差，并对它们进行维护和更新。如果把路标也放进状态的话，由于视觉SLAM 中路标数量很大，这个存储量是相当可观的，且与状态量呈平方增长（因为要存储协方差矩阵）。因此，EKF SLAM 普遍被认为不可适用于大型场景。

---

7.迭代扩展卡尔曼滤波（IEKF）

由于非线性模型中做了线性化近似，当非线性程度越强时，误差就会较大。但是，由于线性化的工作点离真值越近，线性化的误差就越小，因此解决该问题的一个方法是，通过迭代逐渐找到准确的线性化点，从而提高精度。
在EKF的推导中，仅改变观测的线性化观测点：
$$z_k\approx h(x_{op,k},0)+{\mathbf{H}}_k(x_k-x_{op,k})+{\mathbf{C}}_k{n}_k$$
定义卡尔曼增益：
$${\mathbf{K}}_k={\Sigma }_{xy}{\Sigma }_{yy}^{-1}={\overline{\mathbf{P}}}_k{H}_k^T(H_k{\overline{\mathbf{P}}}_k{H}_k^T+{\mathbf{C}}_k\mathbf{Q}{\mathbf{C}}_k^T{)}^{-1}$$
在卡尔曼增益的基础上：
$${\hat{x}}_k={\overline{x}}_k+{\mathbf{K}}_k((z_k-H_k{\overline{x}}_k)-(z_{op,k}-H({\overline{x}}_k))$$
滤波过程中，反复执行这2个公式，以上次的后验均值作为本次的线性化工作点，即可达到减小非线性误差的目的。需要注意的是，在这种滤波模式下，后验方差应放在最后一步进行。

8.其他滤波器的优缺点

8.1 MSCKF

MSCKF的目标是解决EKF的维数爆炸问题，也就是EKF讨论的第三点。传统EKF-SLAM将特征点加入到状态向量中与IMU状态一起估计，当环境很大时，特征点会非常多，状态向量维数会变得非常大。SCKF不是将特征点加入到状态向量，而是将不同时刻的位姿加入到状态向量，特征点会被多个传感器看到，从而在多个传感器状态（Multi-State）之间形成几何约束（Constraint），进而利用几何约束构建观测模型对EKF进行update。由于传感器位姿的个数会远小于特征点的个数，MSCKF状态向量的维度相较EKF-SLAM大大降低，历史的相机状态会不断移除，只维持固定个数的的相机位姿（Sliding Window），从而对MSCKF后端的计算量进行限定。
学习参考链接及论文：
1.A Multi-State Constraint Kalman Filter for Vision-aided Inertial Navigation
2.Improving the Accuracy of EKF-Based Visual-Inertial Odometry
3. MSCKF那些事（一）MSCKF算法简介
4. MSCKF那些事（二）S-MSCKF试用与源码解析

9.卡尔曼滤波-系统方程离散化

离散化推导过程：
给定连续时间线性随机系统（即线性随机微分方程）：
$$\dot{\mathbf{X}}(t)=\mathbf{F}(t)\mathbf{X}(t)+\mathbf{G}(t)w(t)$$
根据线性系统理论，上公式的等效离散化形式为：
$${\mathbf{X}}_k={\Phi }_{k/k-1}{\mathbf{X}}_{k-1}+{\eta }_{k-1}$$
上面公式中，
$$\begin{gathered} {\mathbf{X}}_k=\mathbf{X}(t_k) \\ {\Phi }_{k/k-1}=\Phi (t_k,t_{k-1})\approx e^{{\int }_{t_{k-1}}^{t_k}\mathbf{F}(\tau )d\tau } \\ {\eta }_{k-1}={\int }_{t_{k-1}}^{t_k}\Phi (t_k,\tau )\mathbf{G}(\tau )w(\tau )d\tau \end{gathered}$$
记离散化时间间隔$T_s=t_k-t_{k-1}$，当$\mathbf{F}(t)$在较短的积分区间$[t_{k-1},t_k]$内变化不太剧烈时，且设$\mathbf{F}(t_{k-1})T_s\ll \mathbf{I}$,则进一步转移矩阵可以近似为如下：
$${\Phi }_{k/k-1}=\Phi (t_k,t_{k-1})\approx e^{\mathbf{F}(t_{k-1})T_s}=\mathbf{I}+\mathbf{F}(t_{k-1})T_s+{\mathbf{F}}^2(t_{k-1})\frac{T_s^2}{2!}+{\mathbf{F}}^3(t_{k-1})\frac{T_s^3}{3!}.......\approx \mathbf{I}+\mathbf{F}(t_{k-1})T_s$$
${\eta }_{k-1}$是关于高斯白噪声的线性变换，其结果仍是正态分布的随机向量，所以可以用均值，方差，也就是一，二阶统计特征来描述和等效${\eta }_{k-1}$。
最终得到离散化的公式如下：
$${\mathbf{X}}_k={\Phi }_{k/k-1}{\mathbf{X}}_{k-1}+{\Gamma }_{k-1}{w}_{k-1}$$
其中：
$${\Gamma }_{k-1}\approx [\mathbf{I}+\mathbf{F}(t_{k-1})T_s]\mathbf{G}(k-1)\approx \mathbf{G}(k-1)$$

参考：
视觉SLAM十四讲，高翔