目录
2.5动态规划算法实现------公共序列问题
2.5.1最长公共子序列问题
2.5.1.1问题
2.5.1.2动态规划与枚举法(穷举法、列举法)
2.5.1.3确定动态规则(DP、状态转移方程)、初始值
2.5.1.4动态规划算法代码实现
2.5.2最长公共连续子序列(最长公共子串)问题
2.5.2.1问题
2.5.2.2确定动态规则(DP、状态转移方程)、初始值
2.5.2.3动态规划算法代码实现
2.5动态规划算法实现------公共序列问题
2.5.1最长公共子序列问题
2.5.1.1问题
最长公共子序列(longest common subsequence, LCS),给定两个序列A和B,返回它们的最长的公共子序列的长度。
计算机的序列是指序列的元素在代码中呈现出的顺序与内存存储顺序一致,在计算机中序列是可以通过索引来引用的。在python中字符串、列表、元组都是序列。
子序列是保持原各字符串中的顺序,比如:字符串’ ehjkf’和’ bhfk’,它们的公共最长子序列为’hk’,但不是’ hfk’,因为这种在另一个字符串中的顺序是不同的。
子序列可以是连续的和不连续的,这里的连续是指子序列中的元素在原序列中是不间隔、不间断的,也即在原序列中也是相邻(紧邻)的,这里的连续类似连贯的意思。最长公共子序列就是可以连续也可以不连续中最长的一个公共子序列,也就是讲,最长公共子序列不区分连续和不连续问题,只要是最长的公共子序列即可。
2.5.1.2动态规划与枚举法(穷举法、列举法)
子序列是保持原各字符串中的顺序的,这也确保了动态规划算法的两层循环遍历时状态之间依次关系,也即隐藏着一种顺序(这个顺序不是指循环顺序)关系。前面讲到的通配符匹配问题或正则表达式匹配问题也都有顺序特点。本题如果是找出公共元素的个数,这时候实际不符合动态规划的状态之间的依次关系了,不是动态规划问题,而是适合计算机的枚举法(穷举法、列举法),也是通过循环来实现。枚举法(穷举法、列举法)适合循环遍历中不隐含着顺序(这个顺序不是指循环顺序)关系,而列举所有符合条件的结果。而且使用枚举法,循环中索引i、j的变化最好是相对固定的变化形式(比如:索引i、j以步长1变化),否则,会增加代码的复杂性(比如:在枚举时要判断索引i,j变化),这时枚举方法不太适合。
下面算法就是枚举法求解两个字符串的公共元素的个数。
sr1='aehjkf'
sr2='bhfk'
k=0
for i in sr1:
for j in sr2:
if i==j:
k+=1
print(k)
运行结果:
![]()
代码使用枚举法计算两个字符串的公共元素的个数为3,而这两个字符串的最长公共子序列为’hk’,长度为2。下面我们介绍动态规划算法求解最长公共子序列长度问题,我们可以看到循环遍历中实际隐藏着状态之间的依次关系。
2.5.1.3确定动态规则(DP、状态转移方程)、初始值
(1)直接相关状态
本题是找出序列中最长公共子序列的长度(也即最长公共子序列的元素的个数),实际也是匹配的过程,只是这种匹配是单个元素的匹配,每匹配成功一个,公共子序列的长度也增加了一个。由于是逐个元素的匹配,而且保持原各序列中的顺序,当前匹配到的公共子序列的元素的个数,是由之前匹配到的个数决定的,这正好符合当前状态受之前的状态的影响。在这个匹配的循环遍历过程中,我们始终选择最多的匹配个数(也就是找出最长的公共子序列的长度),最终能找到最长公共子序列的长度。
这里我们以A和B两个字符串为例来求解最长公共子序列,不妨记A=’xcxrcf’,B=’hxrpgf’。
Python的切片是左闭右开的,因而,A[0:i]不包含A[i]、B[0:j]不包含B[j],下面阅读时注意这一点。
A[0:i]表示字符串A的前i个字符构成的局部字符串,B[0:j] 表示字符串B的前j个字符构成的局部字符串。在计算过程中i,j是随着循环而取值的,我们可以记dp[i][j]是A[0:i]与B[0:j]匹配到的最长公共子序列的长度(个数),当前状态ij的值可以由相邻状态i-1j-1、ij-1、i-1j的值决定,因为状态转移是通过匹配来实现的,相邻状态通过增加元素就可以到达ij状态,而且状态值是过去状态值的一种匹配成功的累计值,且选择最大的一个值,这与前面讲到的通配符匹配问题或正则表达式匹配问题是有区别的,后者虽然也是匹配问题但考察所有的字符是否匹配,这会导致状态值的确定与本题是有差异的。
因此,本题中,dp[i][j]值可以由之前的dp[i-1][j-1]、dp[i][j-1] 、dp[i-1][j]值决定。
(2)当前状态值的确定
下面讨论在不同情形下的状态转移,当前状态ij的状态值dp[i][j]是如何确定的。
①当B[j-1]等于A[i-1]时的状态转移
B[j-1]是字符串B[0:j]的末尾字符,A[i-1]是字符串A[0:i]的末尾字符,由于B[j-1]等于A[i-1], B[0:j]与A[0:i]的最后一个字符能对应匹配,因而,B[0:j]与A[0:i]匹配到元素的最多个数是B[0:j-1]与A[0:i-1] 匹配到元素的最多个数再加1,也即当前状态值dp[i][j]由dp[i-1][j-1]决定了,即dp[i][j]= dp[i-1][j-1]+1。
因为ij状态的末尾元素能匹配成功(B[j-1]等于A[i-1]),因而B[0:j]与A[0:i]的匹配情况由B[0:j-1]与A[0:i-1] 的匹配情况决定,状态值dp[i][j] 由dp[i-1][j-1]决定了。
②当B[j-1]不等于A[i-1]时的状态转移
从i-1j-1、ij-1、i-1j增加元素都可以达到ij状态,这时候,由于B[j-1]不等于A[i-1],达到ij状态时的末尾字符不匹配,因而,ij状态值dp[i][j]由dp[i-1][j-1]、dp[i][j-1] 、dp[i-1][j]中最大值决定,即dp[i][j]=max(dp[i-1][j-1], dp[i][j-1], dp[i-1][j])。
但ij-1、i-1j状态都比i-1j-1状态匹配的次数可能多,因为它们的元素增加了,这也增大了匹配成功的可能性,因而,dp[i-1][j-1]值不会比dp[i][j-1]或dp[i-1][j]高,也就是讲dp[i][j-1]或dp[i-1][j]值不会低于dp[i-1][j-1]。因此,dp[i][j]=max(dp[i-1][j-1], dp[i][j-1], dp[i-1][j])可以简化为dp[i][j]=max(dp[i][j-1], dp[i-1][j])。
(3)动态规则(DP、状态转移方程)
上面的描述可以表示为下面的动态规则(DP、状态转移方程):

因为前面匹配后的下一步就到当前状态,所以当前状态dp[i][j]值是与相邻的状态有关的,dp[i][j]值可以由上述三个直接相关状态转化而来。上面的描述内容也即是普通情况下的动态规则DP,根据这个DP,我们可以计算出新的状态值。
在动态规划算法的两层循环中,外层循环是i,内层循环是j,i、 j与A、B字符串的索引对应,在状态方程中状态之间的关系能体现出匹配关系,在两层循环中,外层循环运行一个i,内层循环j遍历一遍。
(4)初始值
下面我们再来确定初始状态。
初始状态的源头是空字符,若A是空字符,B为非空的字符串,这时匹配个数都为0。若A是非空的字符串,B为空字符,这时匹配个数也都为0。A是空字符,B为空字符,本题是考虑子序列的元素个数,空字符与空字符可以不考虑匹配,不妨记dp[0][0]=0,这有利于上面动态规则(DP、状态转移方程)的计算。
前面我们是从字符串A、B都不为空进行分析,dp[i][j]的索引与字符串的索引是一致的,这种不影响分析,但现在加上刚才增加了空字符这种初始状态,要注意dp[i][j]的索引变成比字符串的索引多一个,如图2-17所示。因此,在代码中注意i、j索引表达的变化,否则,使用不当容易产生异常提示string index out of range。
2.5.1.4动态规划算法代码实现
上面的分析及下面代码的实现可以结合下面图2-17来理解。深黄色方框的状态值由周围灰色的状态决定。
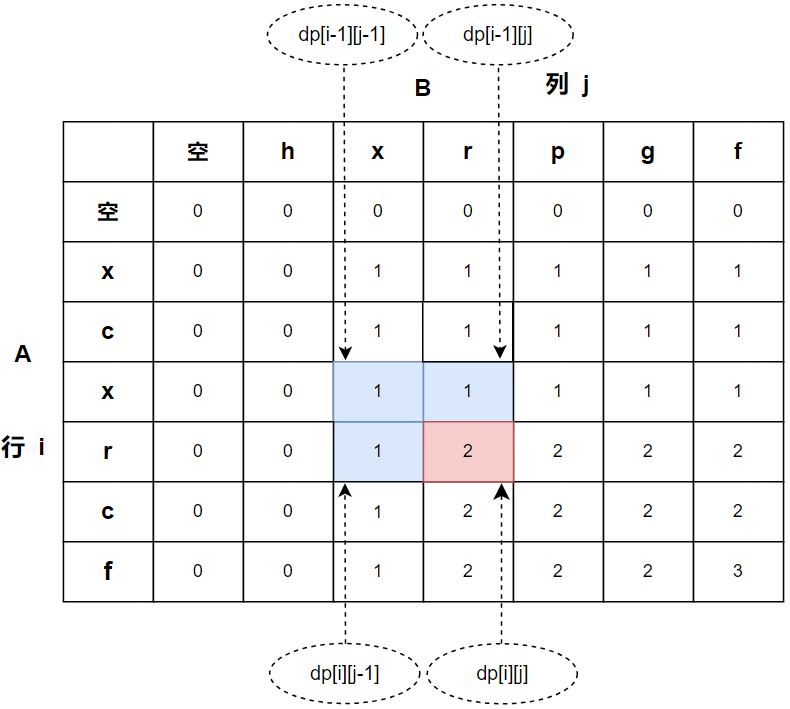
图2-17 最长公共子序列
(1)完整代码
下面程序代码是求解最长公共子序列问题,函数longest_common_subsequence_length()采用动态规划求解最长公共子序列的长度,是按上述分析过程实现的,完全体现了我们上面对动态规划的论述,从代码中就能看到动态规划算法的思想,我们可以结合下面代码来理解动态规划算法在本问题中的应用。
代码中函数find_LCS_dynamic()采用动态规划求解最长公共子序列,函数find_LCS_recursion()采用递归求解最长公共子序列。下面代码中是以字符串序列为例,若是数字型序列,在初始化或存储操作时应该做相应改变以适合数字型的操作特点(比如:在python中用列表存储数字序列,可以用方法append()),其他是一样的。
#A,B为序列,比如:python中的字符串,列表等。
#最长公共子序列的长度。
def longest_common_subsequence_length(A,B):
#增加1,因为初始值增加了空字符有关的行列。
n, m = len(A) + 1, len(B) + 1
#初始化,生成一个二层列表,存放状态值。
dp = [[0] * m for i in range(n)]
#动态规划的初始值,一般来讲,在匹配时空字符不参与匹配,
#因而空字符作为初始状态,状态值为0,上面已经初始化,下面可以省去。
#for i in range(1, n): #空字符的处理
#dp[i][0] = 0
#for j in range(1, m): #空字符的处理
#dp[0][j] = 0
#下面为当前状态值由之前直接相关状态决定,具体含义参见文档中的分析过程。
#这里的i,j索引是dp的索引,0表示初始状态的空字符,因此,索引从1开始。
for i in range(1, n):
for j in range(1, m):
#下面要注意A、B的索引值,它们的索引不是dp对应的索引值,要减去1,
#才刚好对应,因为dp增加了一行一列。
#相等时,当前状态由i-1j-1状态决定。
if A[i - 1] == B[j - 1]:
dp[i][j] = dp[i - 1][j - 1] + 1
else:
#不相等时,当前状态由下面状态最大的状态值决定。
dp[i][j] = max(dp[i - 1][j],dp[i][j - 1])
print('dp逐行输出:')
for i in range(n):
print(dp[i])
return dp
#采用动态规划来求解最长公共子序列。
def find_LCS_dynamic(A,B):
#增加1,因为初始值增加了空字符有关的行列。
n, m = len(A) + 1, len(B) + 1
#生成一个二层列表,存放状态值。初始化的初始值为列表[''],为了方便存放子序列。
dp1 = [[['']] * m for i in range(n)]
#动态规划的初始值,一般来讲,在匹配时空字符不参与匹配,
#因而空字符作为初始状态,为便于计算,状态值记为[''],上面已经初始化,下面可以省去。
#for i in range(1, n): #空字符的处理
#dp1[i][0] = ['']
#for j in range(1, m): #空字符的处理
#dp1[0][j] = ['']
for i in range(1, n):
for j in range(1, m):