时间序列预测 — ARIMA模型原理

ARIMA（Autoregressive Integrated MovingAverage model）差分自回归移动平均模型结合了AR模型（自回归模型）和MA模型（移动平均模型）的基本思想：一个时间点上的标签值既受过去一段时间内的标签值影响，也受过去一段时间内的偶然事件（可以理解为噪音）的影响。这就是说，ARIMA模型假设，标签值是围绕着时间的大趋势而波动的，其中趋势是受历史标签影响构成的，波动是受一段时间内的偶然事件影响构成的，且大趋势本身不一定是稳定的。

在这个中心思想的引导下，ARIMA模型的公式被表示为：

公式的前半段是AR模型，后半段是MA模型中关于“波动”的部分。

1.2 ARIMA模型适用条件

数据序列是平稳的，这意味着均值和方差不应随时间而变化。通过对数变换或差分可以使序列平稳
输入的数据必须是单变量序列，因为ARIMA利用过去的数值来预测未来的数值。

1.3 模型基本步骤

序列平稳化检验；确定d值
确定p值和g值
参数估计与诊断检验
预测未来的值

2 差分（Differencing）

2.1 差分运算的作用

差分运算可以消除数据中激烈的波动，因此可以消除时间序列中的季节性、周期性、节假日等影响。一般我们使用滞后为7的差分消除星期的影响，而使用滞后为12的差分来消除月份的影响（样本所对应的时间单位是月），我们也常常使用滞后4来尝试消除季度所带来的影响（样本所对应的时间单位是季）。差分运算本质是一种信息提取方式，其最擅长提取的关键信息就是数据中的周期性。

2.2 差分运算

首先来看一下ARIMA差分自回归移动平均模型中差分的概念，ARIMA模型内置差分运算，甚至将差分的阶数设置为ARIMA关键的超参数之一，差分运算能提高数据的平稳性。差分是一种用于序列的数学运算，当我们对一个序列进行差分运算，就意味着我们会计算该序列中的不同观测值之间的差异。举例说明，假设我们现在有序列x1:

如果让该序列中执行x1-x2 运算，形成新的蓝色序列。新的序列 y1 的一阶差分结果（First-Order Differencing）。不难发现，一阶差分运算就是令序列中索引更大的值减去与其相邻的索引更小的值，且形成新序列的运算。当序列是时间序列时，一阶差分运算在计算的就是相邻时间点上的标签值的差异。和原始序列相比，差分后序列往往位数更少（序列更短），通常进行一次差分运算，原始的序列会变短1个单位。

在实际进行差分运算时，我们可以改变差分运算的两个相关因子来执行不同的差分：差分的阶数和差分的滞后。

2.3 差分的阶数

先来看差分的阶数：高阶差分意味着多次执行一阶差分。例如，进行二阶差分时（Second-Order Differencing），我们实际上是需要对 x 进行两次一阶差分，即先求解出，再在 y1 的基础上进行一阶差分，求解出 Z：

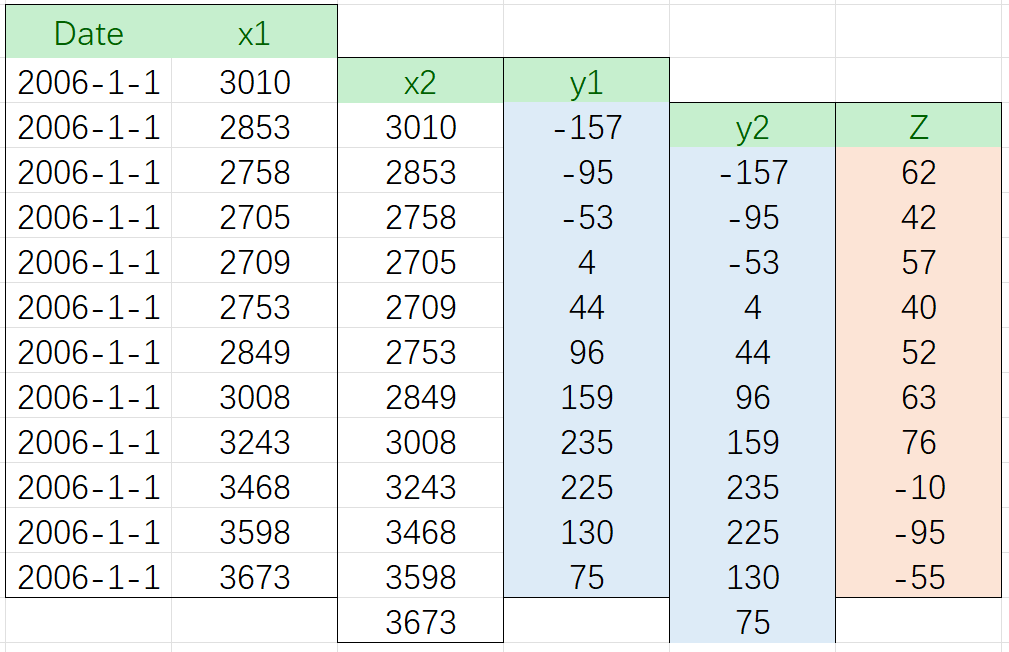
此时 Z 的结果就是序列 x 的二阶差分。因此，n阶差分就是在原始数据基础上进行n次一阶差分。在现实中，我们使用的高阶差分一般阶数不会太高。在ARIMA模型中，超参数d最常见的取值是0、1、2这些很小的数字。

2.4 差分的滞后

差分的滞后与差分的阶数完全不同。正常的一阶差分是滞后为1的差分（lag-1 Differences），这代表在差分运算中，我们让相邻的两个观测值相减，即让间隔为（lag-1）的两个观测值相减。此，当滞后为2时，则代表我们需要让相隔1个值的两个观测值相减。

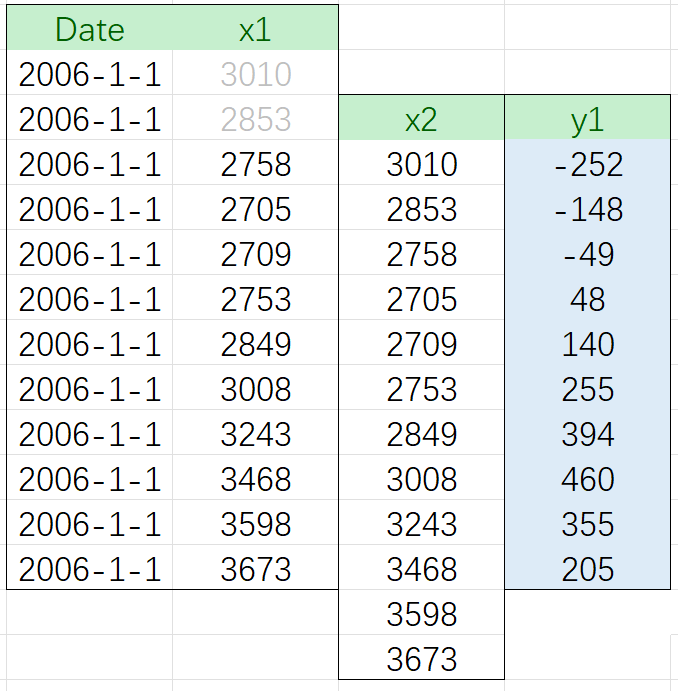
序列 y1 就是序列X的滞后2差分结果。因此，滞后的差分运算就是令序列中索引更大的值减去与其相隔2个样本的索引更小的值，而形成新序列的运算。

带滞后的差分也叫做多步差分，例如，滞后为2的差分就叫做2步差分。相比起平时不怎么使用的高阶差分，多步差分应用非常广泛。在时间序列中，标签往往具备一定的周期性：例如，标签可能随季节有规律地波动（比如在夏季标签值高、在冬季标签值较低等），也可能随一周的时间有规律地波动（比如在周末较高、在工作日较低等）。

2.5 差分运算使用注意点

差分的阶数越高、步数越多，提炼出的信息就越精华？ 事实上，和众多信息提取的过程一样，差分在提取信息的过程中也会产生信息的损失、甚至提炼出“噪音”。阶数越高、步数越多，差分运算丢失的原始信息就会越多，信息的“形变”也就会越厉害，因此我们需要找到合适的阶数和步数，而不是坚持使用高阶或多步差分。

只要数据具有趋势性/周期性，我们就可以利用差分运算将其消除？差分运算的确可以被应用到大部分有趋势性、周期性的时间序列数据上，但它不能解决所有时序数据的问题。

3 数据的平稳性

3.1 数据平稳性的概念

现在我们已经知道差分运算对于时间序列数据的意义了，差分运算带来的平稳性是ARIMA模型能够顺利运行的基本要求。具体地来说，ARIMA模型具有如下基本假设：输入ARIMA的时间序列数据必须是平稳的数据。

d值可从差分阶数来大致判断

在统计学上，稳定的时序数据是始终围绕着一个均值波动，且波动的幅度变化不是很大的数据。在时间变化的同时，序列标签均值明显变化，或不同阶段的波动幅度明显有差异、不均匀的数据都是不稳定的。具体地来说，数据有明显的上升趋势，或下降趋势、数据呈现季节性、周期性、或波动幅度明显越来越大、越来越小的时候，数据都是不稳定的。可以通过ADF来检验数据的平稳性。

3.2 ADF检验概念

前面提到，ARIMA要求时间序列是平稳的，所以一般在研究一段时间序列的时候，第一步都需要进行平稳性检验，除了用肉眼检测的方法，另外比较常用的严格的统计检验方法就是ADF检验，也叫做单位根检验。

ADF检验全称是 Augmented Dickey-Fuller test，顾名思义，ADF是 Dickey-Fuller检验的增广形式。DF检验只能应用于一阶情况，当序列存在高阶的滞后相关时，可以使用ADF检验，所以说ADF是对DF检验的扩展。

3.3 单位根

一阶AR模型，即AR(1)的情况，其模型如下：

当 α1 = 1 ，成为单位根。该模型就是随机游走，我们知道它是不平稳的。例如，当α1 = 1 ，那么前一时刻的对当下时刻的影响是100%的，不会减弱；那么就算是很远的某个时刻，当下对它的影响还是不会消除，所以方差（表现在波动）是受前面所有时刻的影响，是和 t 相关的，因此不平稳；

当 α1 > 1，那么当前时刻的波动不仅受前面时刻的影响，还被放大了，所以不平稳；

当 α1 < 1 的时候，前面时刻的波动对当前时刻的影响会逐渐减小。可以计算此时的自协方差以及自相关系数是一个固定值。所以这种情况下，序列是平稳的。

3.4 ADF检验的原理

ADF检验就是判断序列是否存在单位根：如果序列平稳，就不存在单位根；否则，就会存在单位根。

所以，ADF检验的 H0 假设就是存在单位根，如果得到的显著性检验统计量小于三个置信度（10%，5%，1%），则对应有（90%，95%，99%）的把握来拒绝原假设。

3.5 Python实现ADF检验

from statsmodels.tsa.stattools import adfuller

adfresult = adfuller(regionload['总有功功率（kw）'][150:600])
print(adfresult)

# 输出
(-4.747394852689344, 6.849295111339592e-05, 17, 432, {'1%': -3.445578199334947, '5%': -2.8682536932290876, '10%': -2.570346162765775}, 8736.266503299139)

adf：Test statistic，T检验，假设检验值。
pvalue：假设检验结果。
usedlag：使用的滞后阶数。
nobs：用于ADF回归和计算临界值用到的观测值数目。
icbest：如果autolag不是None的话，返回最大的信息准则值。
resstore：将结果合并为一个dummy。

根据返回值usedlag，d 值可以定为17。

4 确定p、g值

4.1 如何确定p、g值

ARIMA模型中有三个参数：p、q、d，p和q分别控制ARIMA模型中自回归和移动平均的部分，而d则控制输入ARIMA模型的数据被执行的差分的阶数，还可以对ARIMA模型添加参数 lag，以控制差分运算的滞后数（多步差分的步数）。

p值可从偏自相关系数(PACF)图的最大滞后点来大致判断
q值可从自相关系数(ACF)图的最大滞后点来大致判断
d值可从差分阶数来大致判断

4.2 ACF与PACF简介

自相关系数ACF：自相关系数度量的是同一事件在两个不同时期之间的相关程度，形象的讲就是度量自己过去的行为对自己现在的影响。在这里可以通过自相关系数(ACF)图的最大滞后点来大致判断 q 值。

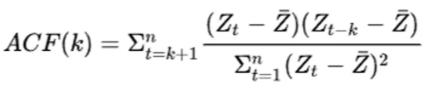
偏自相关系数PACF：计算某一个要素对另一个要素的影响或相关程度时，把其他要素的影响视为常数，即暂不考虑其他要素的影响，而单独研究那两个要素之间的相互关系的密切程度时，称
为偏相关。在这里可以通过偏自相关系数(PACF)图的最大带后点来大致判断 p 值。

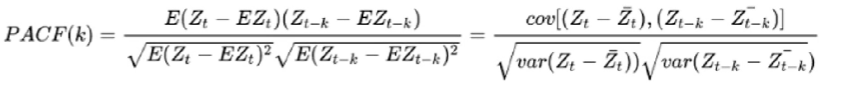
与皮尔逊相关系数高度类似，ACF和PACF的取值范围都是[-1,1]，其中1代表两个序列完全正相关，-1代表两个序列完全负相关，0代表两个序列不相关。

4.3 ACF与PACF

Python代码实现可以直接使用 statsmodels 包进行计算，需要 pip install statsmodels 安装 statsmodels。

import numpy as np
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf

regionload['总有功功率（kw）'][:800].plot()
plot_acf(regionload['总有功功率（kw）'][:800], lags=40, adjusted=False)
plot_pacf(regionload['总有功功率（kw）'][:800], lags=40,  method='ols')
plt.show()

图1为数据集3负荷数据部分，ACF（图2）和PACF（图3）的图像。

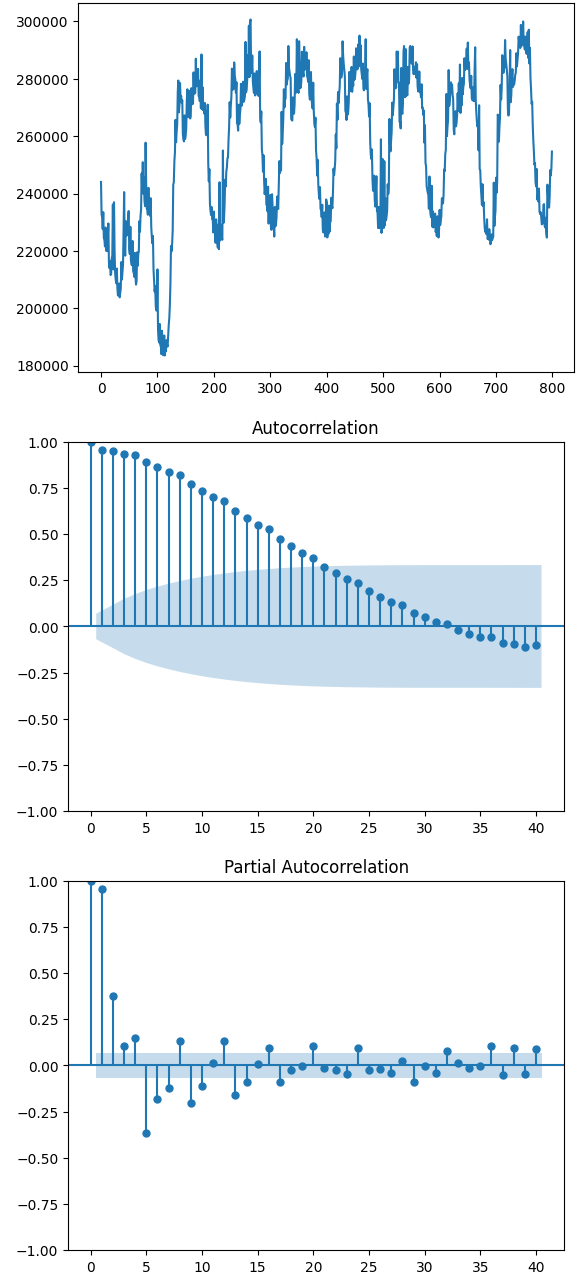
ACF图和PACF图的横坐标相同，都是不同的滞后程度，而纵坐标是当前滞后程度下序列的ACF和PACF值。背景为蓝色的区域代表着95%或99%的置信区间，当ACF/PACF值在蓝色区域之外时，我们就认为当前滞后程度下的ACF/PACF是统计上显著的值，即这个滞后程度下的序列之间的相关性很大程度上是信任的。

通常来说，ACF和PACF图有三种常见的形态：拖尾、截尾、既不拖尾也不截尾。

拖尾：意味着图像呈现按规律衰减、自相关性呈现逐渐减弱的状态（图2），q 值可以定为0。
截尾：特指在某一个滞后程度后ACF/PACF断崖式下跌的状态（图3），例如，滞后0、滞后1对应的ACF都很高，滞后2对应的ACF却断崖式下跌，这种情况被我们称之为“1阶截尾”。特别注意，1阶截尾/n阶截尾中的“阶”是惯用说法，实际上指的是滞后1和滞后n，千万别与高阶差分中的阶混淆，p 值可以定为0。
既不拖尾也不截尾：这种状况下的ACF和PACF图往往看不出什么规律（图3）。

当图像呈现截尾状况的时候，一般截尾的阶数都很低（一般最多不会超过3），这说明该序列中只有非常少的日子对未来有影响。当图像不截尾时，则说明原始数据中的规律较难提取，原始数据可能是平稳序列，可能是白噪音，需要更复杂的时间序列模型来进行规律的提取。

当然，除此之外我们还可能看到其他状态的ACF和PACF图。当ACF或PACF图呈现较强的周期性时，原始序列中大概率也存在较强的周期性（如下图）。当ACF或PACF图呈现较强的趋势性（例如上升或下降）时，原始序列中大概率也存在较强的趋势。