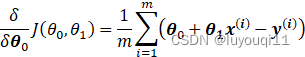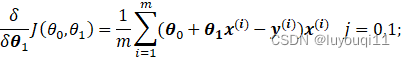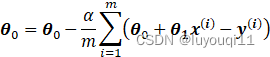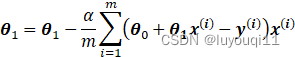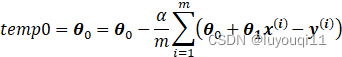梯度下降是迭代法的一种,可以用于求解最小二乘问题(线性和非线性都可以)。
在求解机器学习算法的模型参数，即无约束优化问题时，梯度下降（Gradient Descent）是最常采用的方法之一，另一种常用的方法是最小二乘法。
在求解损失函数的最小值时，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数和模型参数值。
反过来，如果我们需要求解损失函数的最大值，这时就需要用梯度上升法来迭代了。
在机器学习中，基于基本的梯度下降法发展了两种梯度下降方法，分别为随机梯度下降法和批量梯度下降法。
1 梯度定义
在微积分里面，对多元函数的参数求∂偏导数，把求得的各个参数的偏导数以向量的形式写出来，就是梯度。比如函数f(x,y), 分别对x,y求偏导数，求得的梯度向量就是
,简称grad f(x,y)或者∇f(x,y)。对于在点
的具体梯度向量就是
.或者
，如果是3个参数的向量梯度，就是
以此类推。
2 梯度下降与梯度上升
机器学习算法中，在最小化损失函数时，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数，和模型参数值。反过来，如果我们需要求解损失函数的最大值，这时就需要用梯度上升法来迭代了。
梯度下降法和梯度上升法是可以互相转化的。比如我们需要求解代价函数
的最小值，这时我们需要用梯度下降法来迭代求解。
但是实际上，我们可以反过来求解损失函数
的最大值，这时梯度上升法就派上用场了。
下面来详细总结下梯度下降法。
3 梯度下降法求解过程
梯度下降法(gradient descent)是一个最优化算法，常用于机器学习和人工智能当中用来递归性地逼近最小偏差模型。
以两个参数的代价函数
为例。
梯度下降的相关概念
在详细了解梯度下降的算法之前，我们先看看相关的一些概念。
- 步长（Learning rate）：又称学习速率。步长决定了在梯度下降迭代的过程中，每一步沿梯度负方向前进的长度。
- 特征（feature）：指的是样本中输入部分，比如m个单特征的样本
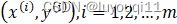，则第一个样本特征为
，第一个样本输出为
。 - 假设函数（hypothesis function）：在监督学习中，为了拟合输入样本，而使用的假设函数，记为
比如对于单个特征的m个样本
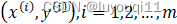，,可以采用拟合函数如下：
- 损失函数（Cost function）：为了评估模型拟合的好坏，通常用损失函数来度量拟合的程度。损失函数极小化，意味着拟合程度最好，对应的模型参数即为最优参数。在线性回归中，损失函数通常为样本输出和假设函数的差取平方。比如对于m个样本
,采用线性回归，损失函数为：
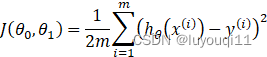
其中则第i个样本特征为
，第i个样本输出为y1
。
详细算法
梯度下降法的算法可以有代数法和矩阵法（也称向量法）两种表示，如果对矩阵分析不熟悉，则代数法更加容易理解。不过矩阵法更加的简洁，且由于使用了矩阵，实现逻辑更加的一目了然。这里先介绍代数法，后介绍矩阵法。
梯度下降法的代数方式描述
1.先决条件：确认优化模型的假设函数和损失函数。
比如对于多元线性回归，
假设函数表示为
其中
为模型参数，
为每个样本的n个特征值。这个表示可以简化，我们增加一个特征
，这样
假设样本数为m，具体为
。
对应于上面的假设函数，损失函数为：
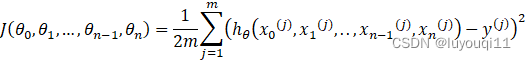
2.算法相关参数初始化：主要是初始化
算法终止距离ε以及步长α。在没有任何先验知识的时候，可以将所有的
初始化为0， 将步长α初始化为1。在调优的时候再优化。
3.算法过程：
第一步：确定当前位置的损失函数的梯度，对于
,其梯度表达式如下：
第二步：用步长乘以损失函数的梯度，得到当前位置下降的距离，即：
第三步：确定是否所有的
,梯度下降的距离都小于ε，
如果小于ε则算法终止，当前所有的
即为最终结果。否则进入步骤4.
第四步：更新所有的θ，对于
，其更新表达式如下：
更新完毕后继续转入第一步。
示例：线性回归的算法过程
下面用线性回归的例子来具体描述梯度下降。
假设我们的样本是
损失函数如前面先决条件所述：
则在算法过程步骤1中对于θi
的偏导数计算如下：
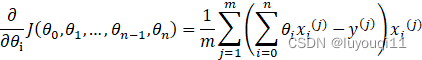
由于样本中没有
,上式中令所有的
。
步骤4中
的更新表达式如下：
从这个例子可以看出当前点的梯度方向是由所有的样本决定的，加
是为了好理解。由于步长
也为常数，他们的乘积也为常数，所以这里
可以用一个常数表示。
在下面会详细讲到的梯度下降法的变种，他们主要的区别就是对样本的采用方法不同。这里我们采用的是用所有样本。
梯度下降法的矩阵方式描述
相对于代数法，要求有一定的矩阵分析的基础知识，尤其是矩阵求导的知识。
1. 先决条件：需要确认优化模型的假设函数和损失函数。
对于多元线性回归，假设函数表示为
其中
为模型参数，
为每个样本的n个特征值。这个表示可以简化，我们增加一个特征
，这样
设向量
则假设函数的矩阵表达方式为：
假设样本个数为m，具体为(x0(j),x1(j),..,xn-1(j),xn(j),yj), j=1,2,…,m
。其矩阵表示形式为：
样本特征为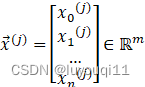
，输出特征为 
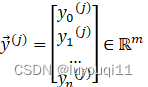，j=1,2…,m
对应于上面的假设函数，损失函数为：
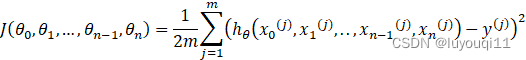
可以简化为：
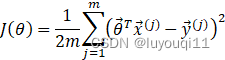
其中， 假设函数
为m×1的向量, Θ为(n+1)×1的向量，里面有n+1个代数法的模型参数。X为m×(n+1)维的矩阵。m代表样本的个数，n+1代表样本的特征数。
损失函数的表达式为：
其中Y是样本的输出向量，维度为mx1.
2. 算法相关参数初始化
Θ向量可以初始化为默认值，或者调优后的值。算法终止距离ε，步长a和代数法比没有变化。
3. 算法过程：
1）确定当前位置的损失函数的梯度，对于Θ
向量,其梯度表达式如下：
2）用步长乘以损失函数的梯度，得到当前位置下降的距离，即
。
3）确定Θ向量里面的每个值,梯度下降的距离都小于ε，如果小于ε则算法终止，当前Θ向量即为最终结果。否则进入步骤4）.
4）更新Θ向量，其更新表达式如下。更新完毕后继续转入步骤1）.
示例：线性回归的算法过程
还是用线性回归的例子来描述具体的算法过程。
损失函数对于Θ向量的偏导数计算如下：
步骤4)中Θ向量的更新表达式如下：
相对于数法，可以看到矩阵法要简洁很多。这里面用到了矩阵求导链式法则，和两个矩阵求导的公式。
公式1：
为向量
公式2：
为标量
梯度下降的算法调优
在使用梯度下降时，需要进行调优。哪些地方需要调优呢？
1. 算法的步长选择。
在前面的算法描述中，我提到取步长为1，但是实际上取值取决于数据样本，可以多取一些值，从大到小，分别运行算法，看看迭代效果，如果损失函数在变小，说明取值有效，否则要增大步长。前面说了。步长太大，会导致迭代过快，甚至有可能错过最优解。步长太小，迭代速度太慢，很长时间算法都不能结束。所以算法的步长需要多次运行后才能得到一个较为优的值。
2. 算法参数的初始值选择。
初始值不同，获得的最小值也有可能不同，因此梯度下降求得的只是局部最小值；当然如果损失函数是凸函数则一定是最优解。由于有局部最优解的风险，需要多次用不同初始值运行算法，关键损失函数的最小值，选择损失函数最小化的初值。
3.归一化。
由于样本不同特征的取值范围不一样，可能导致迭代很慢，为了减少特征取值的影响，可以对特征数据归一化，也就是对于每个特征X，求出它的期望
和标准差std(X)，然后转化为：
这样特征的新期望为0，新方差为1，迭代速度可以大大加快。
4 梯度下降法大家族(BGD,SGD,MBGD)
批量梯度下降法（Batch Gradient Descent）
批量梯度下降法，是梯度下降法最常用的形式，具体做法也就是在更新参数时使用所有的样本来进行更新，这个方法对应于前面示例：线性回归的梯度下降算法，也就是说前面示例：线性回归的梯度下降算法就是批量梯度下降法。
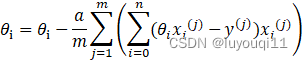
由于我们有m个样本，这里求梯度的时候就用了所有m个样本的梯度数据。
随机梯度下降法（Stochastic Gradient Descent）
随机梯度下降法，其实和批量梯度下降法原理类似，区别在与求梯度时没有用所有的m个样本的数据，而是仅仅选取一个样本j来求梯度。对应的更新公式是：
随机梯度下降法，和批量梯度下降法是两个极端，一个采用所有数据来梯度下降，一个用一个样本来梯度下降。
自然各自的优缺点都非常突出。
对于训练速度来说，随机梯度下降法由于每次仅仅采用一个样本来迭代，训练速度很快，而批量梯度下降法在样本量很大的时候，训练速度不能让人满意。
对于准确度来说，随机梯度下降法用于仅仅用一个样本决定梯度方向，导致解很有可能不是最优。对于收敛速度来说，由于随机梯度下降法一次迭代一个样本，导致迭代方向变化很大，不能很快的收敛到局部最优解。
那么，有没有一个中庸的办法能够结合两种方法的优点呢？有！这就是小批量梯度下降法。
小批量梯度下降法（Mini-batch Gradient Descent）
小批量梯度下降法是批量梯度下降法和随机梯度下降法的折衷，也就是对于m个样本，我们采用x
个样子来迭代，1<x<m。一般可以取x=10，当然根据样本的数据，可以调整这个x的值。对应的更新公式是：
5 梯度下降法和其他无约束优化算法的比较
在机器学习中的无约束优化算法，除了梯度下降以外，还有前面提到的最小二乘法，此外还有牛顿法和拟牛顿法。
梯度下降法和最小二乘法相比，梯度下降法需要选择步长，而最小二乘法不需要。梯度下降法是迭代求解，最小二乘法是计算解析解。如果样本量不算很大，且存在解析解，最小二乘法比起梯度下降法要有优势，计算速度很快。但是如果样本量很大，用最小二乘法由于需要求一个超级大的逆矩阵，这时就很难或者很慢才能求解解析解了，使用迭代的梯度下降法比较有优势。
梯度下降法和牛顿法/拟牛顿法相比，两者都是迭代求解，不过梯度下降法是梯度求解，而牛顿法/拟牛顿法是用二阶的海森矩阵的逆矩阵或伪逆矩阵求解。相对而言，使用牛顿法/拟牛顿法收敛更快。但是每次迭代的时间比梯度下降法长。
6 以假设函数
为例演示梯度下降法
通用步骤
- 代价函数：
- 希望：求合适的参数
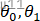使得
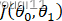最小 - 做法：选择θ0,θ1
初始值(通常都设置为0)，计算Jθ0,θ1
值；改变θ0,θ1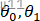
的值，使得Jθ0,θ1
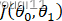减小，直到满足我们的要求最小或局部最小。
因此有：
i
在计算机中更新
的值，必须是同时更新，可以用下列代码实现：
用python实现梯度下降
将使用一个变量实现线性回归，以预测食品卡车的利润。假设你是一家餐馆的首席执行官，正在考虑不同的城市开设一个新的分店。该连锁店已经在各个城市拥有卡车，而且你有来自城市的利润和人口数据。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt'''
样本输入特征数为N (N=1 对于一元线性回归)，输出特征为y。
假设函数：y=theta0+theta1*x1+theta2*x2+...+thetaN*xN
令x0 =1,
x = [x0,x1,x2,...,xN]
theta = [theta0,theta1,theta2,...thetaN]
则有：
y = x * theta.T
样本个数为M, 样本的输入特征矩阵X为 (M行N+1列)，输出特征y为向量(M行1列)
代价函数：cost = sum((X*theta.T-y)^2)/(2*M)
'''def computeCost(X, y, theta):
'''
作用：计算代价函数,向量化来计算参数
:param X: 样本的输入特征，矩阵(M行N+1列)。
:param y: 样本的输出特征，向量(M行1列)
:param theta: parameters，一元线性回归的参数，向量(1行N+1列
:return: 代价函数的值，浮点数
'''
inner = np.power(((X * theta.T) - y), 2)
# print(inner)
return np.sum(inner) / (2 * len(X))def gradientDescent(X, y, theta, alpha, epoch):
'''
作用:获得最终梯度下降后的theta值以及cost
:param X: 输入特性矩阵(M,N+1),一元线性回归N=1，矩阵形状(M,2)
:param y: 输出特性矩阵(1,M)
:param theta: 假设函数参数矩阵(1,N+1)。一元线性回归N=1，矩阵形状(1,2)
:param alpha: 步长，又称学习速率,浮点数。
:param epoch: 要执行的迭代次数，整数。
:return:
'''
# 1 变量初始化，储存数据
# 1.1 初始化参数矩阵为0
np.matrix(np.zeros(theta.shape)) # 初始化一个临时矩阵(1, 2)
# flatten()降维 即返回一个折叠成一维的数组。
# 但是该函数只能适用于numpy对象，即array或者mat，普通的list列表是不行的。
parameters = int(theta.flatten().shape[1]) # 参数theta的数量 2
# print(parameters)
# 1.2 初始化保存每一次迭代计算代价函数值的数组为0
cost = np.zeros(epoch) # 初始化一个ndarray, 包含每次训练后的cost #1000个0的矩阵
# print(cost)
# 1.3 初始化保存每一次迭代计算假设函数参数的数组(epoch,2)为0
counterTheta = np.zeros((epoch, 2)) #1000 * 2的数组
m = X.shape[0] # 样本个数# 2 迭代计算
for i in range(epoch):
'''
使用 vectorization同时更新所有的θ，可以大大提高效率,此处都是相对应的进行计算
X.shape, theta.shape, y.shape, X.shape[0]
((97, 2), (1, 2), (97, 1), 97)
'''
# 相当于theta1 theta2不停做偏导并且更新 theta[theta1, theta2] temp是临时的theta
temp = theta - (alpha / m) * (X * theta.T - y).T * X
theta = temp
counterTheta[i] = theta
cost[i] = computeCost(X, y, theta)
pass
return counterTheta, theta, cost'''
单变量线性回归
'''# 1.Prepare datasets
path = 'D:/dataAnalysis/MachineLearning/ex1data1.txt'
# names添加列名，header用指定的行来作为标题，若原无标题且指定标题则设为None
data = pd.read_csv(path, header=None, names=['Population', 'Profit'])
data.head()
data.describe()
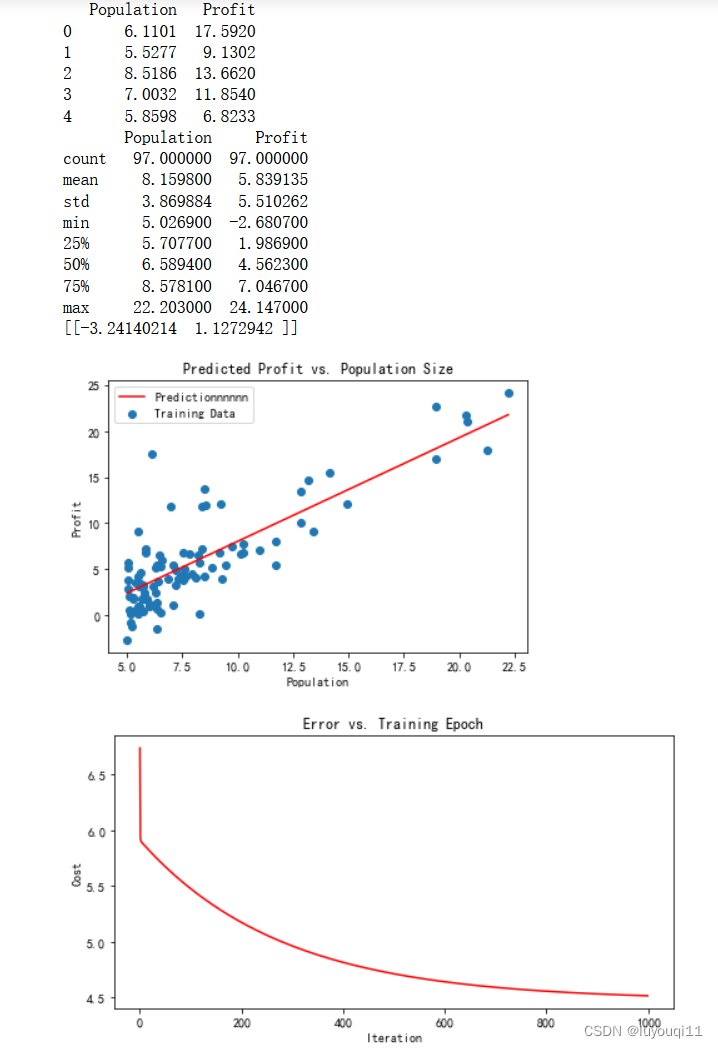
print(data.head())#显示前五行
print(data.describe())# 2 展示散点图，可视化理解数据
#data.plot(kind='scatter', x='Population', y='Profit', figsize=(8,5))
#plt.title("Scatter plot of training data") #添加描述信息
#plt.xlabel("population of city")
#plt.ylabel("profit")
#plt.show()# 3 在数据集前增加1列，值为全1
data.insert(0, 'Ones', 1) # 增加一条第一列，全部数值为1
# print(data)# 4 从表中提取样本输入特征，输出特征
# 变量初始化:set X (training data) and y (target variable)
cols = data.shape[1] # 列数
X = data.iloc[:, 0:cols - 1] # 取前cols-1列，即输入向量
y = data.iloc[:, cols - 1:cols] # 取最后一列作为目标向量
# print(X.head()) # 观察下 X (训练集) and y (目标变量)是否正确.
# print(y.head())# 5 将样本输入特征，输出特征转化为矩阵
X = np.matrix(X.values)
y = np.matrix(y.values)
theta = np.matrix([0,0]) # theta 是一个(1,2)矩阵
computeCost(X, y, theta)
# print(X.shape, y.shape, theta.shape) # 查看各自的行列数
# print(computeCost(X, y, theta)) # 32.072733877455676# 6 定义学习速率，迭代次数
alpha = 0.01 # 学习速率α
epoch = 1000 # 要执行的迭代次数# 7 梯度下将法求解
counterTheta, final_theta, cost = gradientDescent(X, y, theta, alpha, epoch)
computeCost(X, y, final_theta)
# print(computeCost(X, y, final_theta)) # 4.515955503078912# 8 预测值
x = np.linspace(data.Population.min(), data.Population.max(), 100) # xlabel start:返回样本数据开始点 stop:返回样本数据结束点 num:生成的样本数据量，默认为50
f = final_theta[0, 0] + (final_theta[0, 1] * x) # ylabel profit
print(final_theta)# 9 可视化
# 9.1 绘制样本离散图和预测曲线
fig1, ax = plt.subplots(figsize=(6, 4)) # 尺寸
ax.scatter(data.Population, data.Profit, label='Training Data') # 样本的离散值
ax.plot(x, f, 'r', label='Predictionnnnnn') # 预测曲线：横坐标 纵坐标 颜色 标签
ax.legend(loc=2) # 2表示在左上角
ax.set_xlabel('Population')
ax.set_ylabel('Profit')
ax.set_title('Predicted Profit vs. Population Size')# 9.2 绘制代价函数曲线
fig2, ax = plt.subplots(figsize=(8, 4))
ax.plot(np.arange(epoch), cost, 'r') # 横坐标 纵坐标 颜色
ax.set_xlabel('Iteration')
ax.set_ylabel('Cost')
ax.set_title('Error vs. Training Epoch')
plt.show()
其中ex1data1.txt的内容为：
6.1101,17.592
5.5277,9.1302
8.5186,13.662
7.0032,11.854
5.8598,6.8233
8.3829,11.886
7.4764,4.3483
8.5781,12
6.4862,6.5987
5.0546,3.8166
5.7107,3.2522
14.164,15.505
5.734,3.1551
8.4084,7.2258
5.6407,0.71618
5.3794,3.5129
6.3654,5.3048
5.1301,0.56077
6.4296,3.6518
7.0708,5.3893
6.1891,3.1386
20.27,21.767
5.4901,4.263
6.3261,5.1875
5.5649,3.0825
18.945,22.638
12.828,13.501
10.957,7.0467
13.176,14.692
22.203,24.147
5.2524,-1.22
6.5894,5.9966
9.2482,12.134
5.8918,1.8495
8.2111,6.5426
7.9334,4.5623
8.0959,4.1164
5.6063,3.3928
12.836,10.117
6.3534,5.4974
5.4069,0.55657
6.8825,3.9115
11.708,5.3854
5.7737,2.4406
7.8247,6.7318
7.0931,1.0463
5.0702,5.1337
5.8014,1.844
11.7,8.0043
5.5416,1.0179
7.5402,6.7504
5.3077,1.8396
7.4239,4.2885
7.6031,4.9981
6.3328,1.4233
6.3589,-1.4211
6.2742,2.4756
5.6397,4.6042
9.3102,3.9624
9.4536,5.4141
8.8254,5.1694
5.1793,-0.74279
21.279,17.929
14.908,12.054
18.959,17.054
7.2182,4.8852
8.2951,5.7442
10.236,7.7754
5.4994,1.0173
20.341,20.992
10.136,6.6799
7.3345,4.0259
6.0062,1.2784
7.2259,3.3411
5.0269,-2.6807
6.5479,0.29678
7.5386,3.8845
5.0365,5.7014
10.274,6.7526
5.1077,2.0576
5.7292,0.47953
5.1884,0.20421
6.3557,0.67861
9.7687,7.5435
6.5159,5.3436
8.5172,4.2415
9.1802,6.7981
6.002,0.92695
5.5204,0.152
5.0594,2.8214
5.7077,1.8451
7.6366,4.2959
5.8707,7.2029
5.3054,1.9869
8.2934,0.14454
13.394,9.0551
5.4369,0.61705
运行后结果如下：
