【AI绘图学习笔记】卷积网络前序——卷积背后的数学原理

CNN解释器地址：CNN Explainer
CNN解释器文献：CNN Explainer: Learning Convolutional Neural Networks with Interactive Visualization
CNN github地址：https://github.com/poloclub/cnn-explainer
3B1B数学原理视频：那么……什么是卷积？
DTF:What is a Discrete Fourier Transform?

---

卷积网络

卷积网络也叫卷积神经网络(CNN) ，是一种专门用来处理具有类似网络结构的数据的神经网络。例如时间序列数据（可以认为是在时间轴上有规律地采样形成的一维网格）和图像数据（可以看作二维的像素网格）。卷积是一种特殊的线性运算，卷积网络指的是那些至少在网络的一层中使用卷积运算来替代一般的矩阵乘法运算的神经网络。

卷积运算

假设我们有两个骰子，现在让你给出骰子的分布律，你可以画出上图的这个矩阵，对角线上的元素都是相同的点数，那么就可以按照对角线元素的数量来给出分布律

能不能想到另一种方法来表示呢？我们可以把两组骰子可能的结果分别放到两行，将其中一行进行反转，那么可以得到下面这个图像

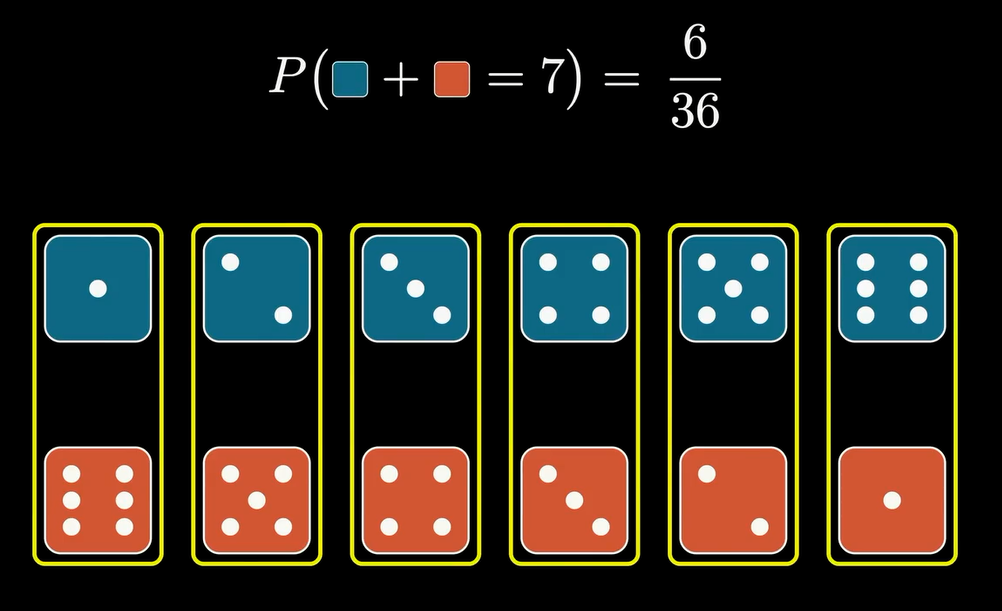
这样所有点数为7的骰子组合就会这样纵向对齐，那么如果我们将下行的骰子滑动至最左边，然后依次向右滑动，如下所示

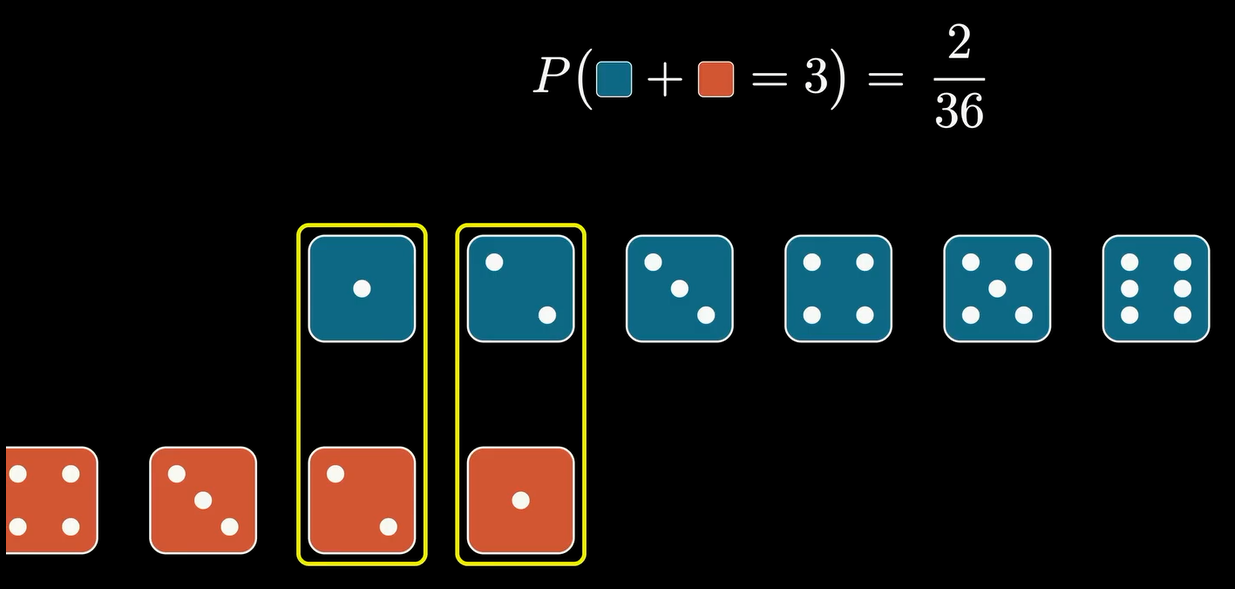
如果用上下组合只有一对时就是1和1，代表了点数为1的分布为$P(1)=\frac{1}{36}$,然后向右滑动一格，那么点数为3的组合就有两对：$P(3)=\frac{2}{36}$，再向右滑动一格，则点数为4的组合就有三对…以此类推，不断右移下列的骰子直到没有组合了为止，我们就能得到完整的分布律。

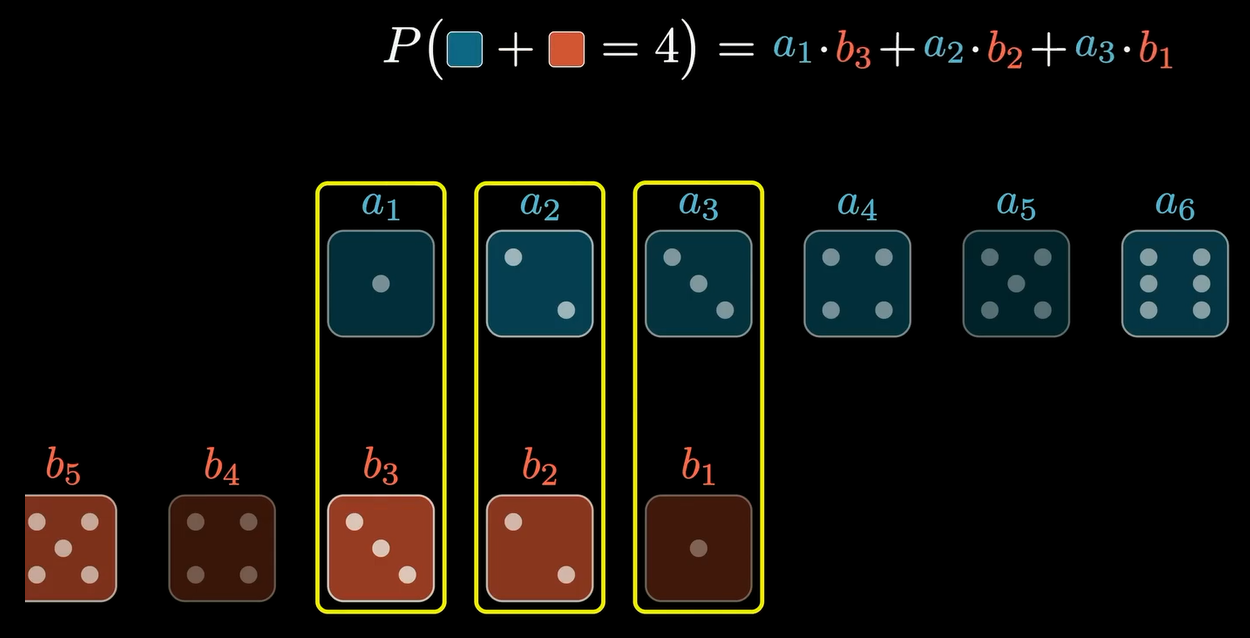
在刚刚的问题中，骰子每面朝上的概率默认是$\frac{1}{6}$，现在让我们给出非均匀分布的骰子概率，我们可以将整个骰子的概率看作一个数组，那么对应每个骰子的概率是不同元素，例如$a\mathrm{1...}a6,b\mathrm{1...}b6$那么计算概率组合就可以用这些元素来进行表示。

在这个过程中，我们运用某种运算将A和B数组的值交汇计算，我们就将这种运算方式称为卷积。我们将上面产生的新数列称为$a_i与b_i$的卷积，数列包含了上述的11个值。

另一种思考卷积的方式是列一个表格，计算各个组合的乘积并将对角线进行相加：

我们可以把卷积公式写为$(a\ast b{)}_n=\sum _{\underset{i+j=n}{i,j}}{a}_i\cdot b_j$，其中$\ast$代表了卷积。

那么如果问你(1,2,3)和(4,5,6)的卷积结果，你就可以想象把后面的数组翻转一下然后进行滑动，最后得到了一个新的数组(4,13,28,27,18)(你可以验算一下)。接下来我们看一看一些概率的计算：

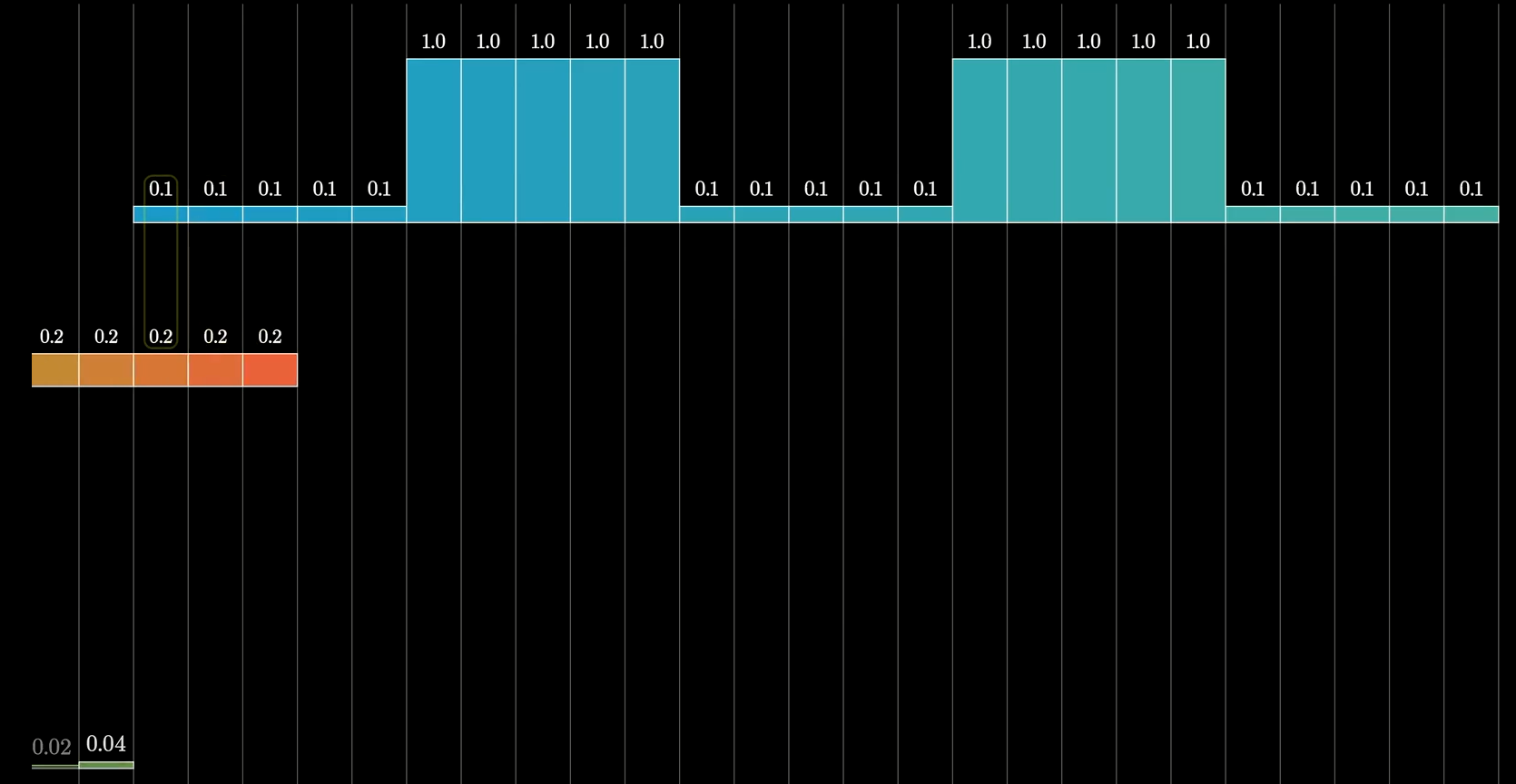
让我们不不断推动下面这个数组，

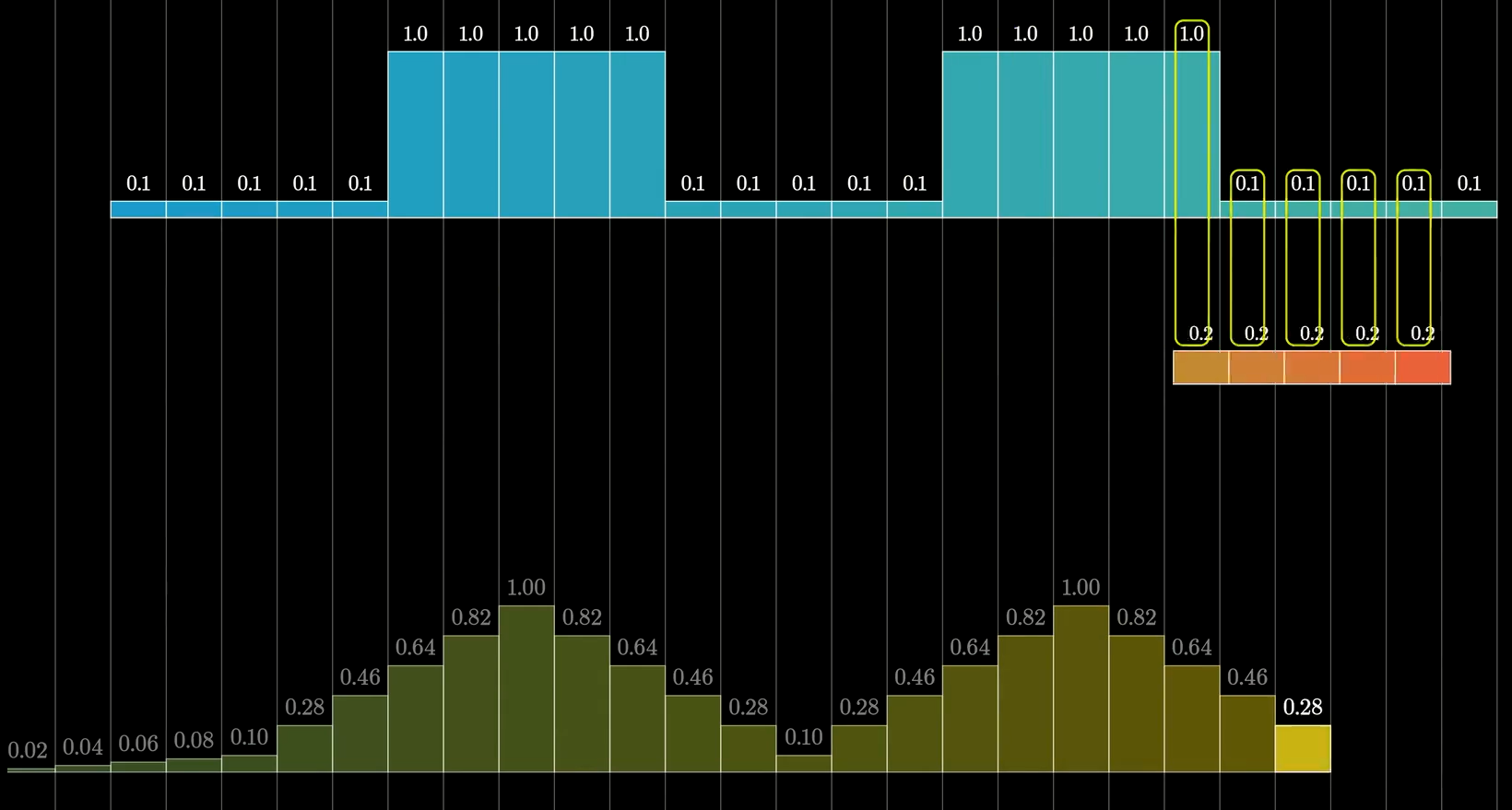
当滑动数组的所有元素完全和上面的数组进行组合了之后，我们发现一个很有意思的事情，由于滑动数组每个元素的概率都是0.20，因此当与上面五个元素进行计算了之后，例如如图:
$$\begin{gathered} 1\ast 0.2+0.1\ast 0.2+0.1\ast 0.2+0.1\ast 0.2+0.1\ast 0.2 \\ =(1+0.1+0.1+0.1+0.1)\ast \frac{1}{5} \\ =0.28 \end{gathered}$$
因此当下面的概率全部一样时，即是对上面对应的元素进行平均值运算。如果我们将下面的概率看作为权重的话，卷积操作的概率运算就相当于对原概率的权重运算。由于原数据我们可以看到值之间落差较大，因此进行了卷积的权重运算后可以将原数据转化为下方的更平滑的版本。

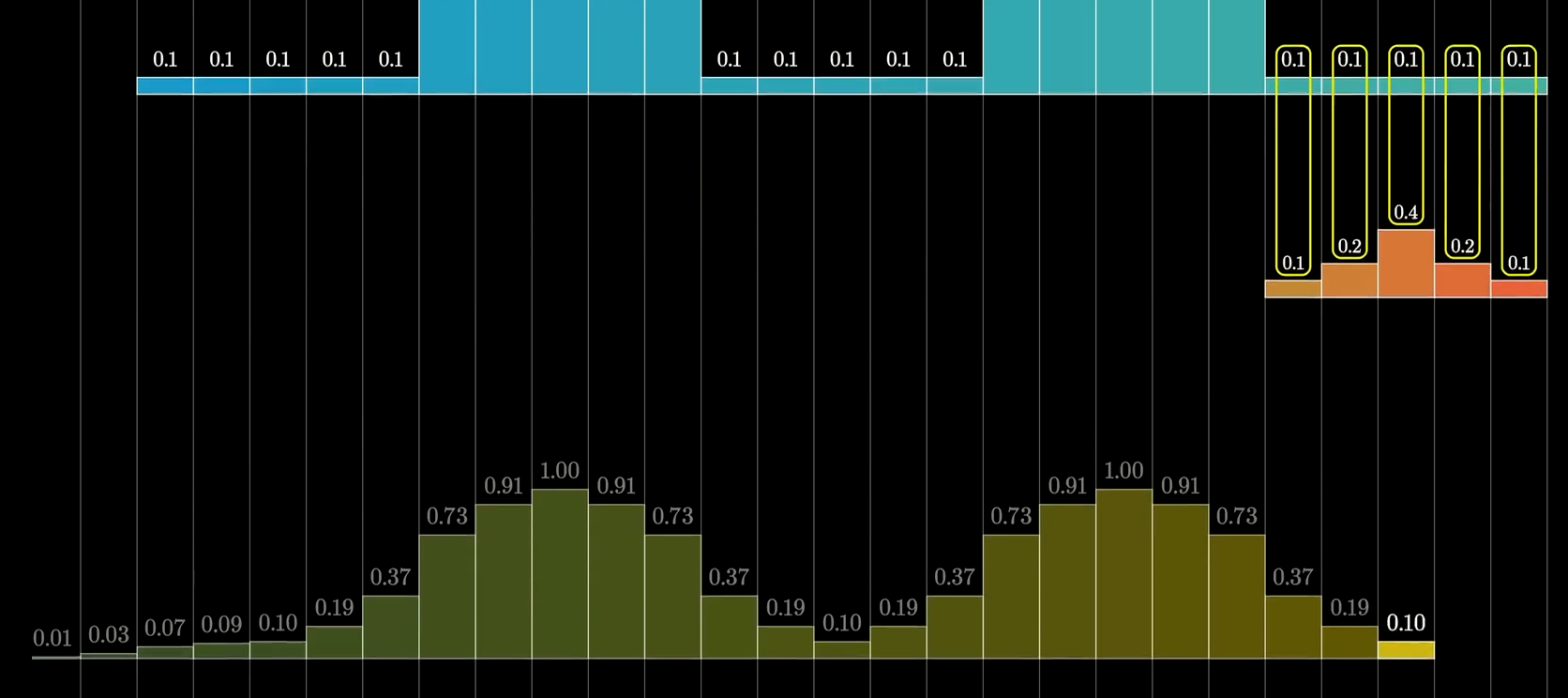
那么当我们的权重如上所示，则滑动平均会给中间值更大的权重，虽然权重不同，但最后的结果依然是原数据的平滑版本。因此卷积也可以视为一种平滑化方法。

因此，如果对图像进行卷积操作，则会发现一个有趣的现象，那就是原图像会变得更加模糊，这是因为与滑动窗口进行卷积运算后RGB色彩在数值上也更加平滑了。

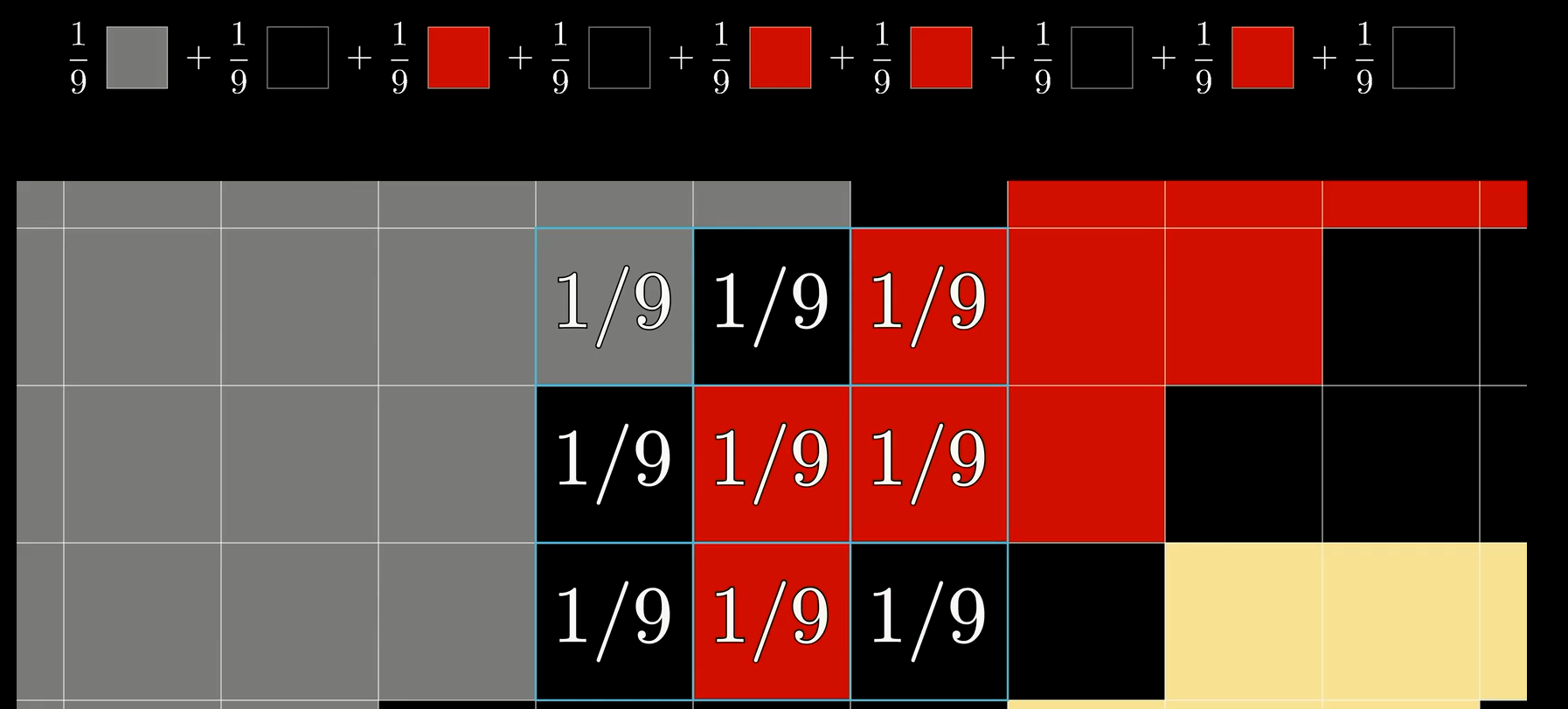
简单理解的话，图像卷积就是对窗口内的色块进行了权重相加，实际上在计算机中由于通常为RGB图像，因此可以看作一个三维向量计算，

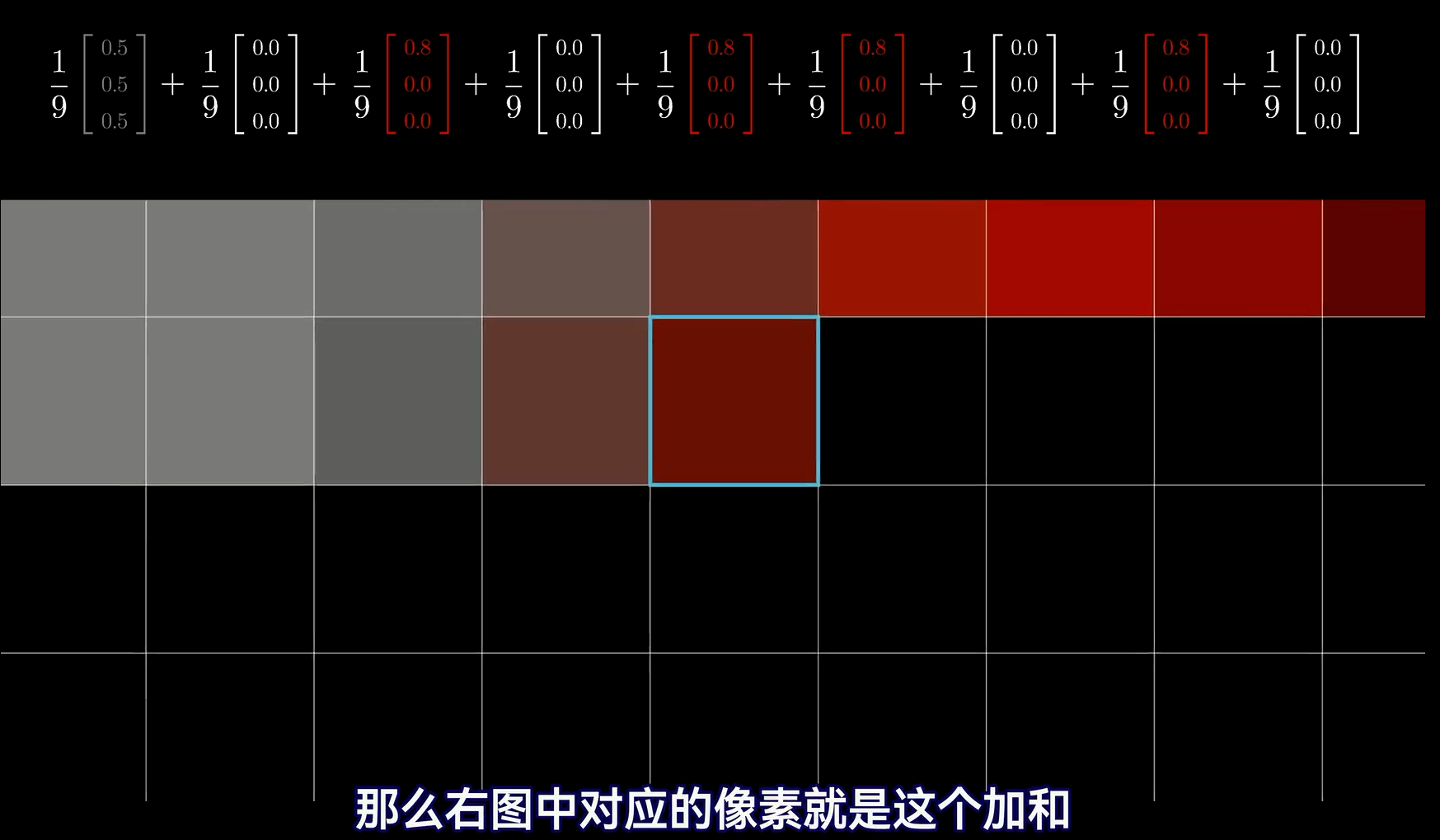
因此图像上的卷积操作相当于当前像素和周围其他像素的RBG值进行了加权混合，就得到了一个比原图更模糊的版本，实际上卷积操作是对右上角这个奇怪矩阵的卷积，当我们进行卷积计算的时候则是将它旋转180度后进行计算。

当我们进行卷积的矩阵在三维上满足正态分布/高斯分布(你可以将值看作高度),越中间的元素给的权重越多，越边缘越少。如果你学过PS那么就应该很熟悉这种方法，我们将这种平滑方法（模糊方法）称为高斯模糊或者高斯平滑 ，

接下来我们用灰度图来表示要处理的图像，因为RGB需要三维向量，灰度可以用单个值表示。在灰度图中，白色代表1，黑色代表0，因此我们来看上面这个例子，我们可以把矩阵分为三列，第一列为正数权值，第二列为0，第三列为负数权值，是第一列的相反数。

因此我们来看上图这个例子，明显结果是$1\ast (-0.25)+1\ast (-0.5)+1\ast (-0.25)=-1$，我们最后的结果用蓝色表示正数，红色表示负数。因此最后的卷积结果是一个代表-1的红色格子。

现在移动到了一个新的区域，我们发现九宫格区块上的所有灰度都是相同的，那么设为a，计算后不难发现最后的权重值相加总和为0，因为所有格子的灰度相同。因此这个格子是0（用黑色表示）

由于这个卷积的矩阵中间列的值是0，因此中间列不影响计算，它的作用实际上是找出左列和右列灰度值不一样的区块，因此实际上功能相当于对图像中所有竖向方向上产生了颜色变化的色块边界进行描边。

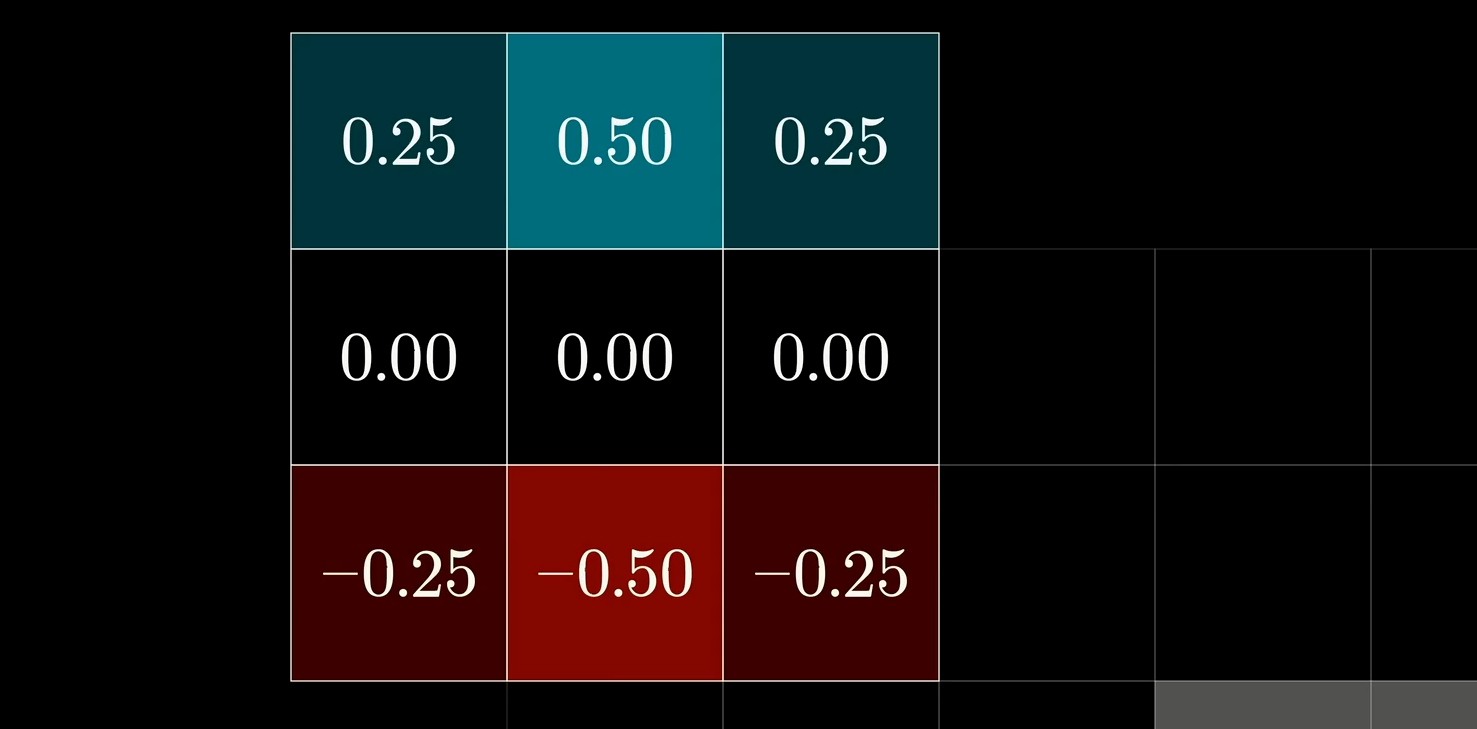
那么同理如果我们对这个矩阵侧翻，使得它检测行的灰度，那么功能就相当于对图像中所有横向方向上产生了颜色变化的色块边界进行描边。

我们将这个用于卷积操作的小网格称之为Kernel卷积核(想起来核函数，核技巧），其巧妙之处在于，只需要选取不同的核，我们就能产生不同的图像处理效果，不仅是模糊化边界检测，也能对图像进行锐化

卷积神经网络的思路就是用数据来算出应该选取什么样的核，这取决于神经网络检测的目标。

在数学上计算卷积的时候，最终获得的矩阵总要比原来的大。在计算机进行计算的时候，我们只考虑核和计算对象（输入长度）完全覆盖时的那些部分，在此基础上扩大来匹配最大的输入长度。

然而翻转核来进行计算似乎有点抽象，我们还是推荐使用矩阵并进行对角相加来计算。实际上卷积我们似乎早就学过了，例如下图所示：

$(1,2,3)\ast (4,5,6)$这个卷积操作，对比下面的多项式乘法会发现，卷积值和多项式系数是对应的，并且我们用矩阵对角相加的方法来计算的方法，本质上就是一个对多项式的全乘积的展开方法，对角线求和就是合并同类项，这个过程和卷积的过程实际上是一模一样的。

我们知道任意一条曲线都可以进行多项式拟合，并且n个点可以唯一地确定n-1阶多项式。那么如果卷积就相当于多项式相乘，那么两个函数$f(x)g(x)$相乘就是两个多项式相乘，那么最终$f(x)g(x)$的系数就相当于多项式系数的卷积！所以两个函数相乘的结果相当于对其有限点的系数进行卷积重现。上面的方法被称为快速卷积算法。

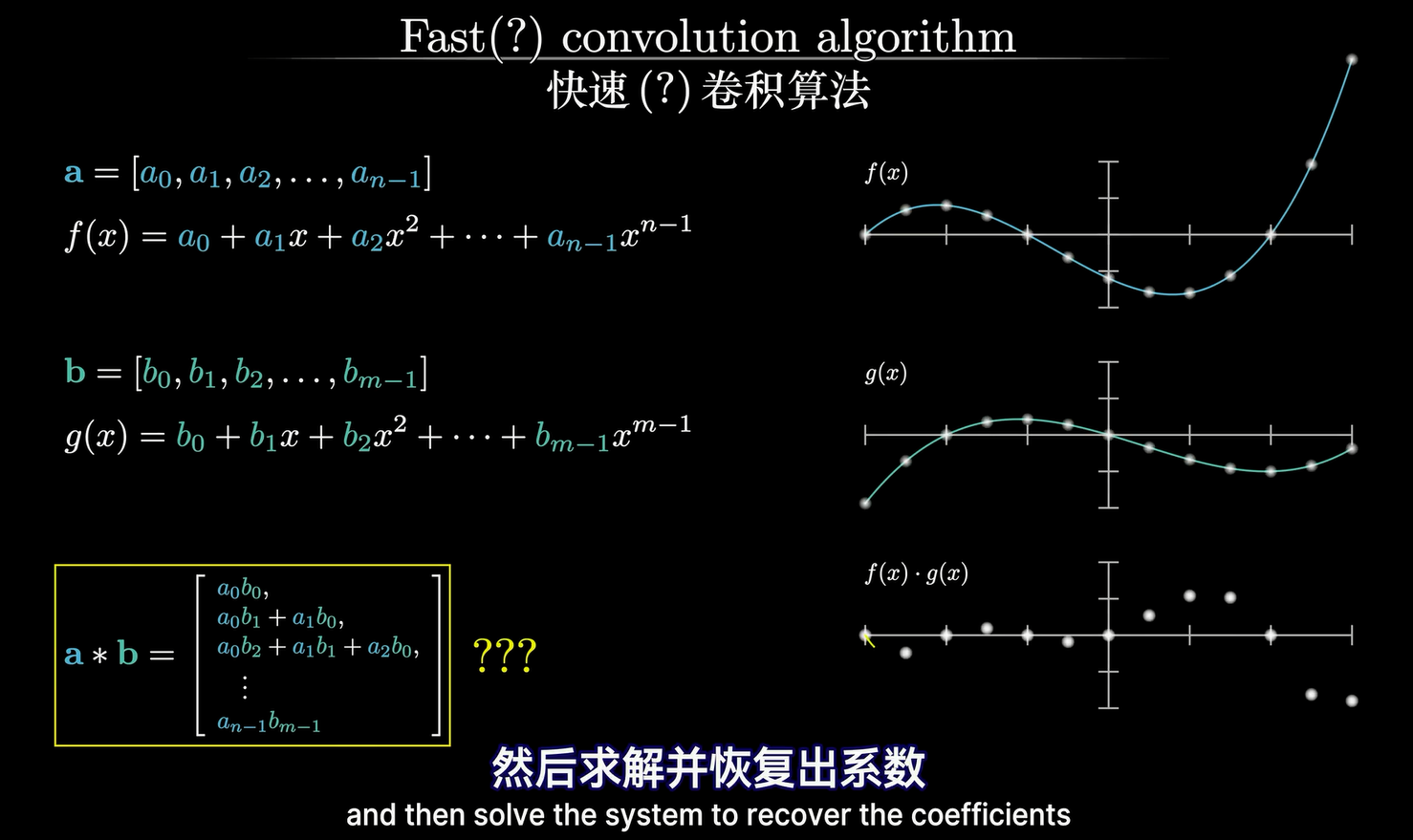
那么现在我们用8个取样点来表示一个七次项的函数$h(x)$，我们带入这八个点(0到7),我们发现所组成的正好是一个线性方程组，因此解出系数$c_i$就相当于带入取样点来解这个方程组。因此要计算$f(x)g(x)$，就需要解出两个方程组的系数，再将这些系数进行卷积计算。

然而如果需要先解方程再卷积，复杂度依然是$O(N^2)$,也就是直接对系数进行卷积，和对多项式直接进行相乘完全没有区别，所谓的快速卷积和快速一点关系都没有，现在为了使得卷积操作更加快速，我们需要学习傅里叶变换。

---

傅里叶变换

博主并不是通信专业的，对信号啥的不懂，只能大致解说一下，单纯地把信号看作函数即可）

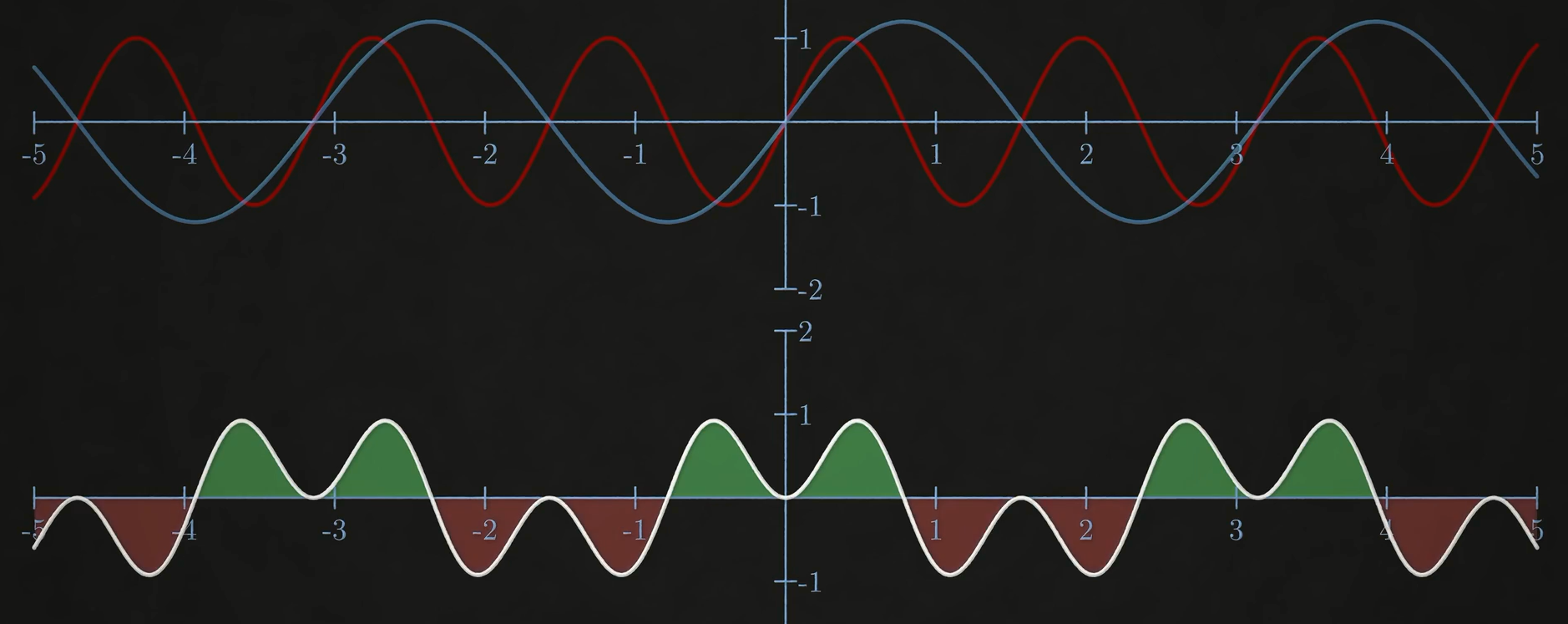
假设我们想要知道一个信号是否由某个正弦波构成的，例如图上我们想要求的这个蓝色信号和给出的一个红色正弦波

让我们将这两个信号波重叠，同号的区间相加，异号的区间相加，你会发现同号区间的面积等于异号区间的面积。现在将这两个函数相乘得到一个新的函数，如果X轴上方的区域面积正好等于X轴下方的区域面积，也就是二者面积之和为0，这就代表这个频率的正弦波并不是我们信号的一部分。

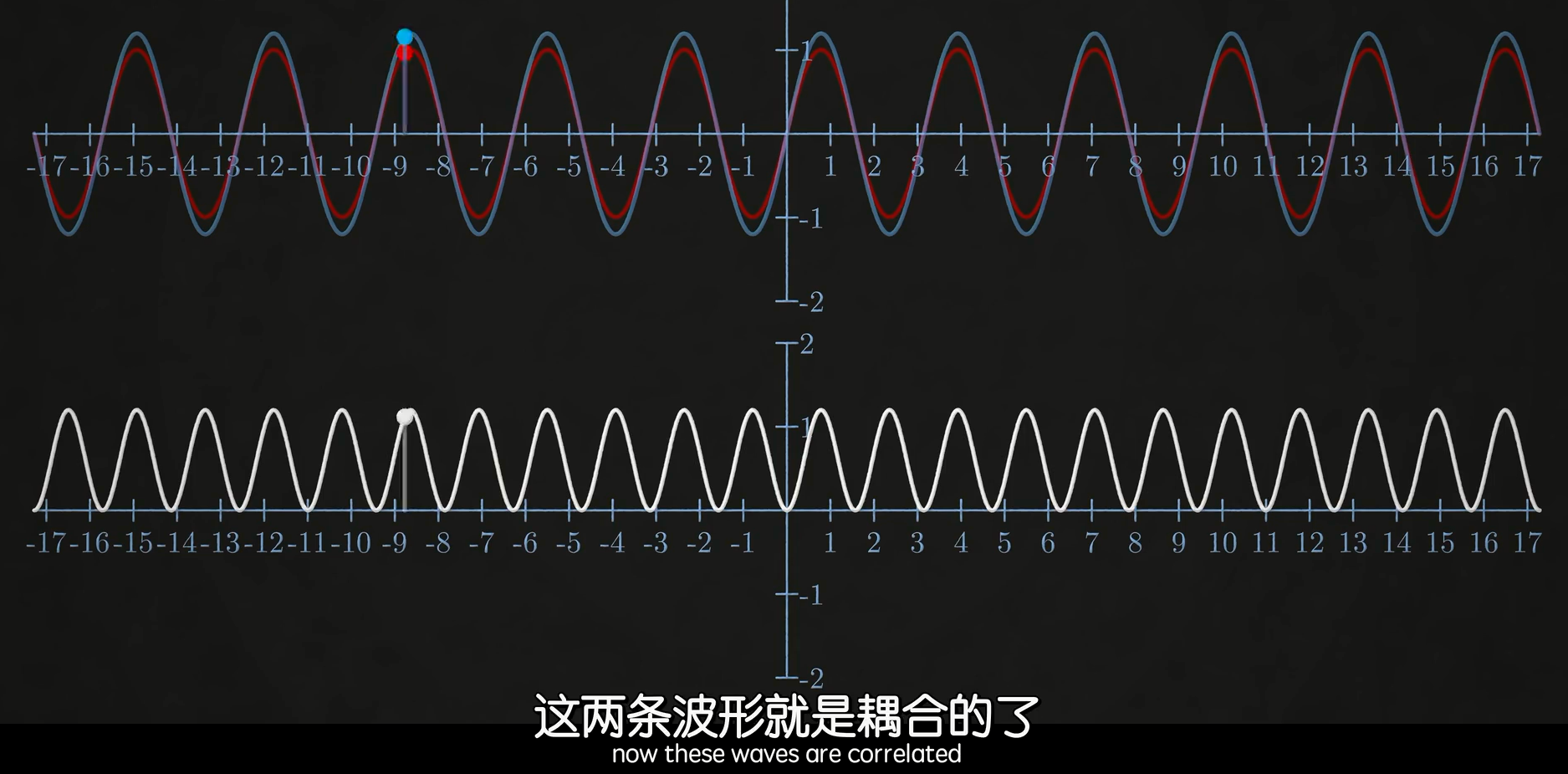
那么让我们调整红色正弦波的频率，直到两者的乘积表示面积只在X轴上方，此时说明两条波形耦合了（很好理解，因为X轴上方的值相乘为正，X轴下方的值是负数×负数也是正的），此时说明这个红色正弦波是我们所求的蓝色信号的一部分。

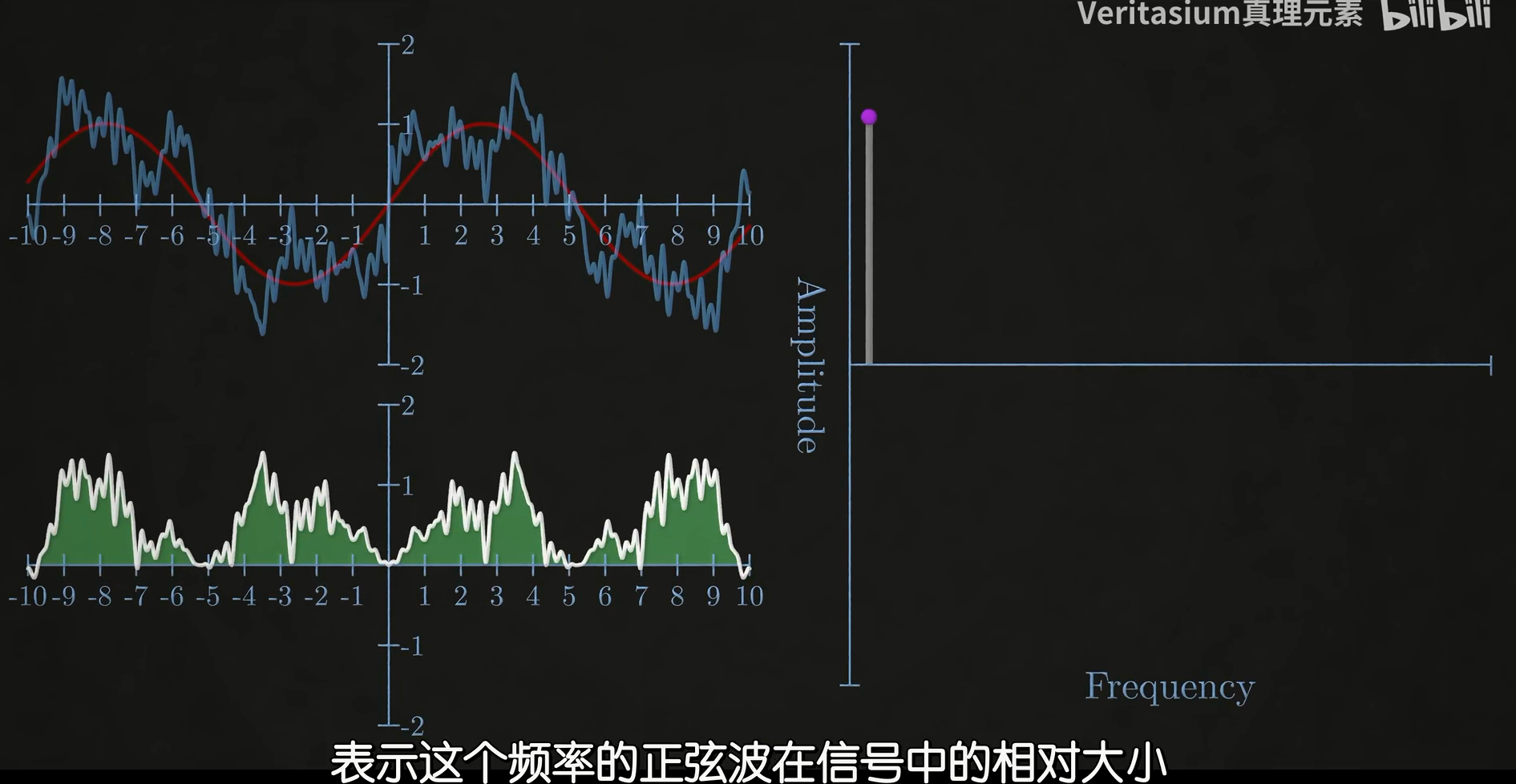
现在让我们将问题变复杂，让蓝色的信号变成多种频率的正弦波组合，这个结论依旧成立，并且产生的这个面积代表了这个频率的正弦波在信号中的相对大小。

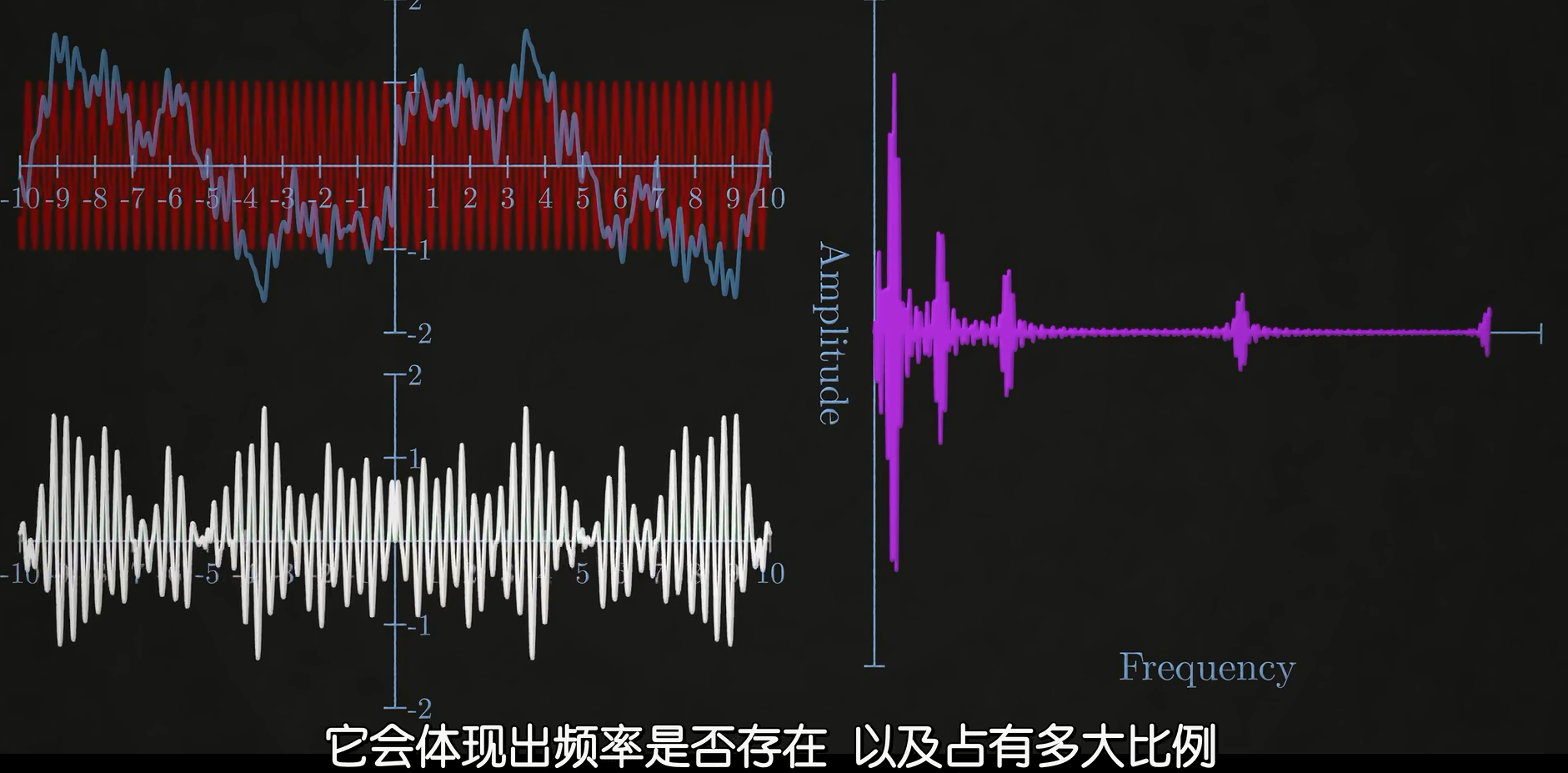
让我们不断调整红色正弦波的频率，我们会得到一个频谱图，它体现了某种频率的正弦波是否存在于信号，以及占有了多大的比例。如果我们将这个信号分别与正弦波和余弦波相乘，分别计算出两者的强度，

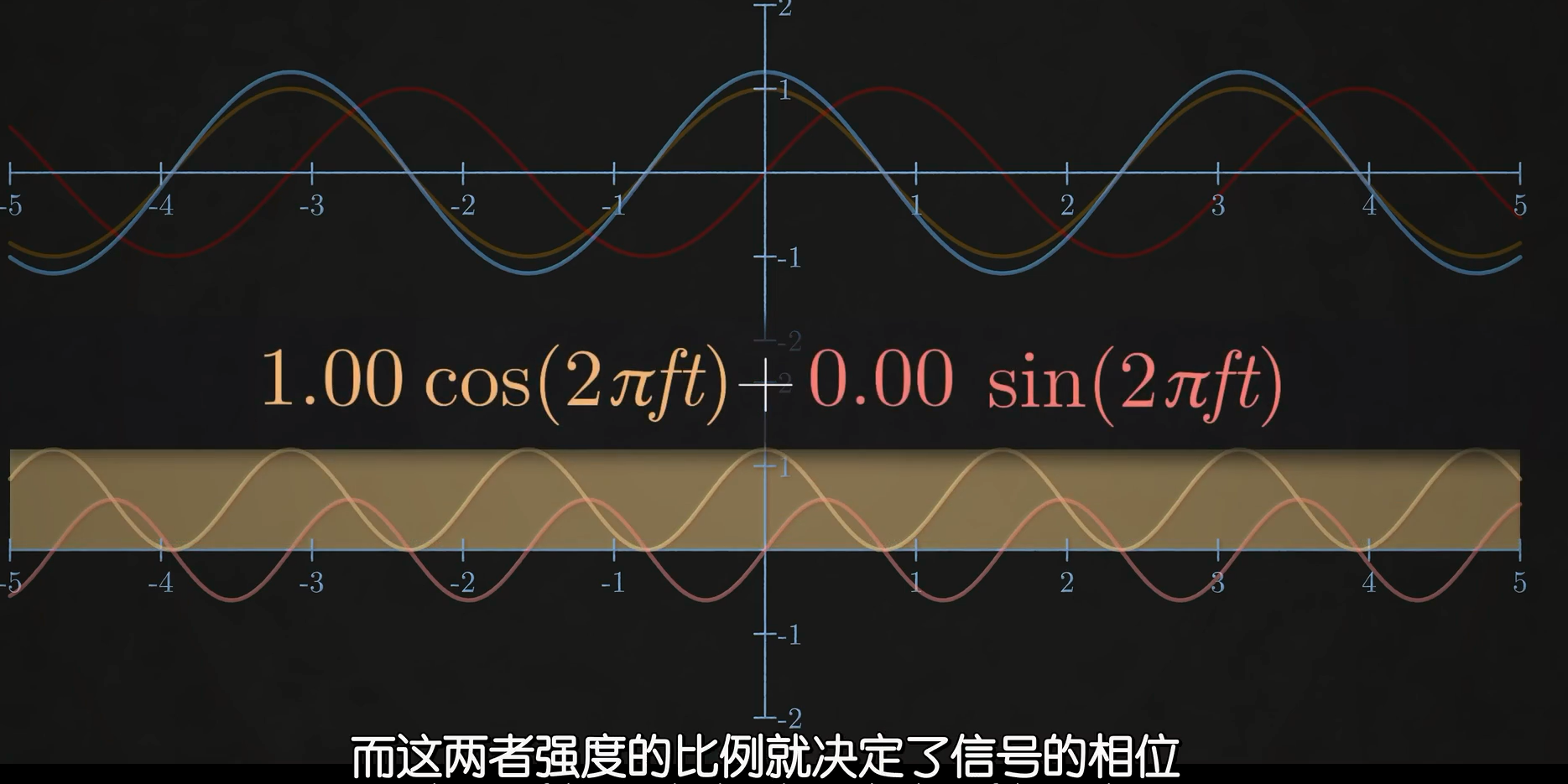
现在我们将用余弦波表示蓝色的信号，那么即使我们用频率相同的正弦波与其相乘，曲线与坐标轴围成的面积仍然是0，（因为余弦波里不存在正弦波啊！），我们将二者在信号中的强度比例称为信号的相位，你可以像上式一样表示为两种波形的成分，或者我们可以用指数形式来表示：那就是用欧拉公式。

根据欧拉公式$cosx+isinx=e^{(ix)}$,
因此带入傅里叶变换公式$cos(2\pi ft)+isin(2\pi ft)=e^{(i2\pi ft)}$,其中$i$代表虚数，$f$代表频率，$2\pi f$代表角频率$\omega$， $t$代表周期。

进行变换可以得到$信号\times cos(2\pi ft)+i信号\times sin(2\pi ft)=信号\times e^{i2\pi ft}$，式子的左边可以看作复数$a+bi$的形式，即复数的实部是余弦波的强度，而虚部是正弦波的强度。

为什么我们说欧拉公式表示更好，因为我们知道正余弦是周期函数，放在笛卡尔坐标系里，会无限延长，但是如果我们将其放在复平面内，那么正余弦就会呈现出一定的周期性。

---

离散傅里叶变换DFT

现在假设我们有一列向量，如图所示，现在我们想要计算它的总长$\hat{s}[0]$,用几何的方式来表示就是将其首尾相连

现在我们把n个向量放到复平面上，如图所示：

$\zeta =e^{-2\pi i/N}$是复平面上的n次单位根，将复平面分割为了n个单位角度$\theta$。如果带入欧拉公式$cos\theta +isin\theta =e^{(i\theta )}$的话，我们可以发现上式$\hat{s}[1]$实际上就是对对应的原向量应用了欧拉公式变换到复平面上。

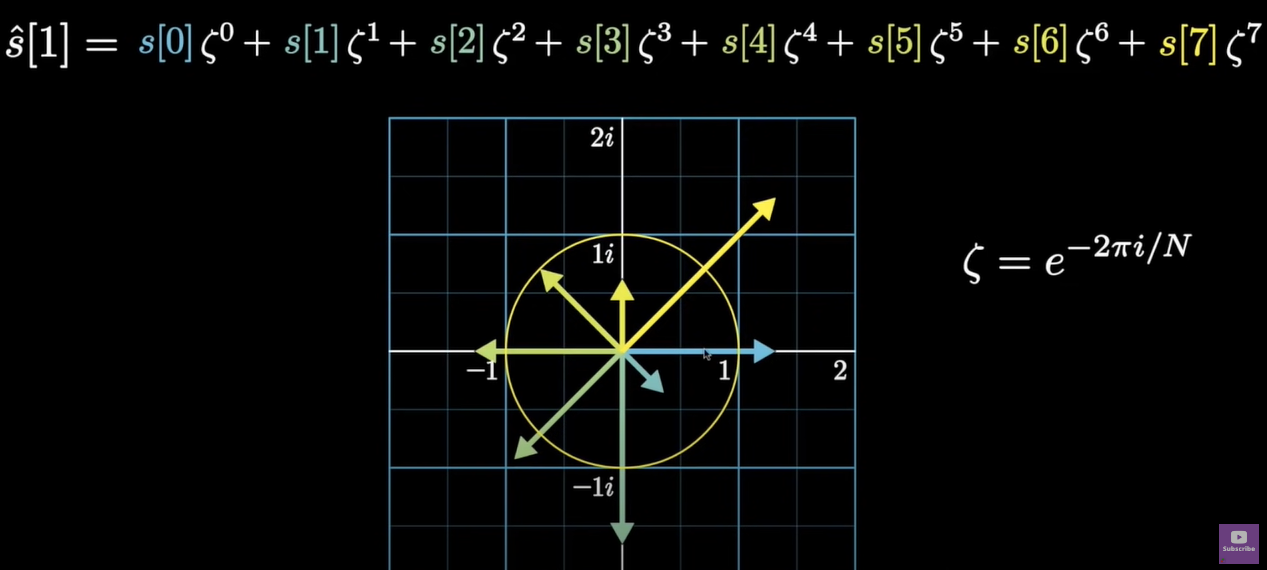
对应的横轴上的向量为$s[0]$，然后顺时针序号增加。
那么现在让我们在余弦波上来取样频率，看看在复平面上的图像会变成什么样？

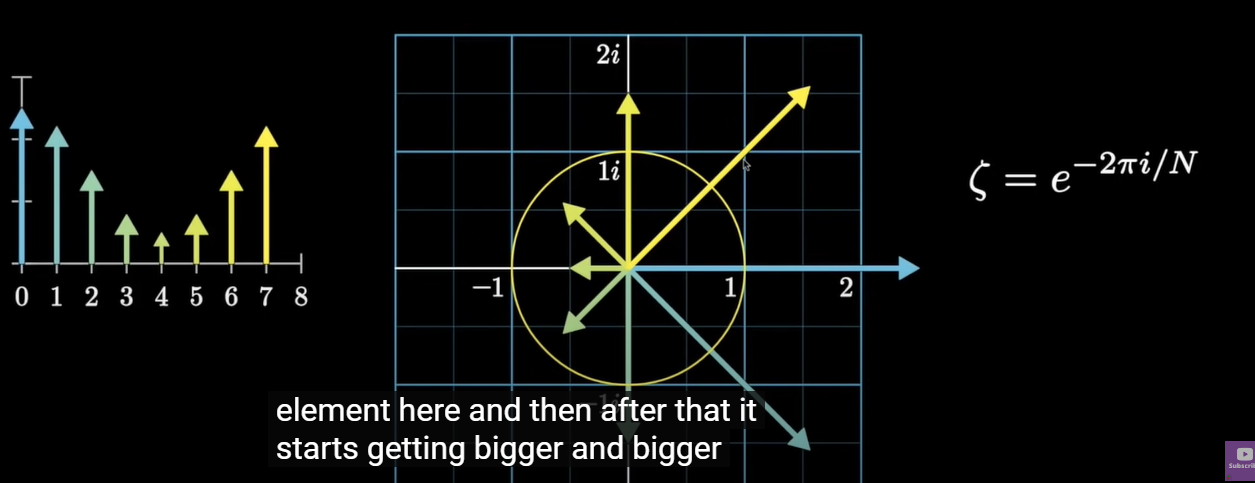
明显在实轴正方向上对应最长的向量，随后顺时针上向量长逐渐变小，当到达$s[4]$时即实轴负方向向量最短，然后顺时针又变大

现在我们对$\zeta$乘以双倍的单位根，也就是对应${\zeta }^{0,2,\mathrm{4...2}n}$，那么原来8个向量$s$分布的总角度正好是复平面$pi$，现在翻倍则是$2\pi$。对应的如果是余弦波，那么代表了余弦波图像范围从原来的$[0,\pi ]$变为了$[0,2\pi ]$，这意味着相同的采样点，我们采取了更高的频率。可以看到对应的图像上在$s[4]=s[0]$说明向量在复平面上已经移动了$\pi$度。

---

快速傅里叶算法

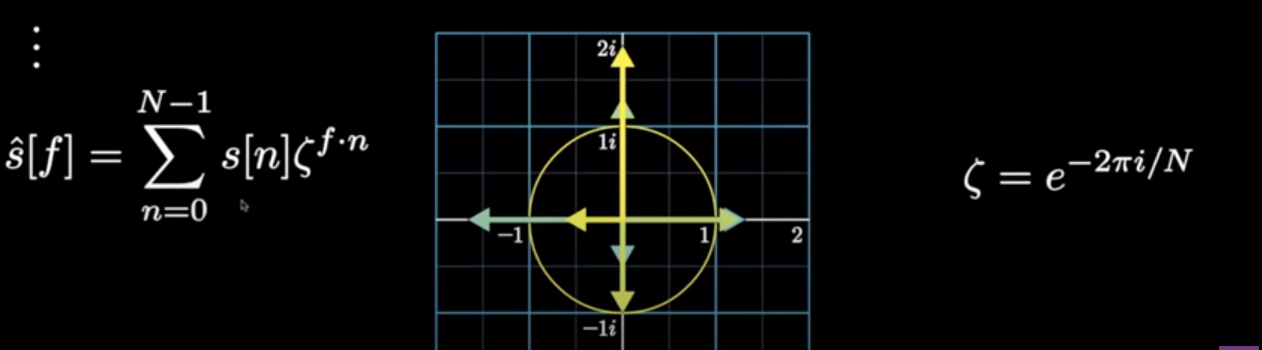
刚才所讲的，同样可以推广到n次单位根，最终会发现向量在整个复平面上经过了n周。而实际上由于绕了n圈，因此例如${\zeta }^8和{\zeta }^0$是一样的，也就是周期为8，那么如果我们用[0,7]来表示$\hat{s}[f]$，那么可以简化为：

现在就回到了我们刚才抛出的快速卷积算法，c是我们对要求的系数，
原本带入样本点后求解方程组是很复杂的，而现在就会有很多的冗余的相同项，这样我们的方程组就更好解了。这样复杂度就从$O(N^2)$下降到$O(Nlog(N))$，这些输出集合$h(\omega )$被我们称为$(c_i)$系数的离散傅里叶变换，

感谢这些冗余，使得我们才能更快速地把系数转换到这些输出点。输入数组越大减少的计算越多，并且我们也可以反向地从输入对应到系数。

如果我们对卷积前的函数系数进行了FFT求解，之后将两个结果逐点相乘，最后做一个FFT逆变换，我们就得到了一个计算卷积的取巧方法。并且复杂度成了$O(NlogN)$。

---

本节并没有详细介绍数学公式，作为一种计算方式只需知道卷积背后是如何进行运算的即可。