CNN解释器地址:CNN Explainer
CNN解释器文献:CNN Explainer: Learning Convolutional Neural Networks with Interactive Visualization
CNN github地址:https://github.com/poloclub/cnn-explainer
卷积运算
假设我们正在用激光传感器追踪一艘宇宙飞船的位置,我们的激光传感器给出一个单独的输出 x ( t ) x(t) x(t),表示宇宙飞船在时刻 t t t的位置。 x x x和 t t t都是实值的,这意味着我们可以在任意时刻从传感器中读出飞船的位置。
现在假设我们的传感器受到了一定程度的噪声干扰,为了得到飞船位置的低噪声估计,我们对得到的测量结果进行平均。显然,时间上越近的测量结果越相关,因此我们采用一种加权平均的方法,对于最近的测量结果赋予更高的权重。我们可以采用一个加权函数 ω ( a ) \omega(a) ω(a)来实现,其中 a a a代表测量结果距离当前时刻的时间间隔,如果我们对任意时刻都采用这种加权平均的操作,就得到了一个新的对于飞船位置的平滑估计函数 s s s :
s ( t ) = ∫ x ( a ) ω ( t − a ) d a s(t)=\int x(a)\omega(t-a)da s(t)=∫x(a)ω(t−a)da
直观一点表示的话,其实就是我们在前序得到的这个图
我们将这种运算称为卷积,卷积通常用星号表示:
s ( t ) = ( x ∗ w ) ( t ) s(t)=(x*w)(t) s(t)=(x∗w)(t)
其中 ω \omega ω必须是一个有效的概率密度函数(权值之和为1),另外当参数为负数值时, ω \omega ω的取值必须为0,否则他它预测未来。不过这些限制也仅仅是对上述的函数平滑而言。
我们通常将 x x x称为输入, ω \omega ω称为卷积核或者核函数,输出有时也被我们称为特征映射。
在使用计算机处理上述函数的时候,是不存在连续值的,因此我们只能用离散值来计算,因此上面的连续值卷积也可以被表示为离散形式的卷积:
s ( t ) = ( x ∗ w ) ( t ) = ∑ a = − ∞ ∞ x ( a ) ω ( t − a ) s(t)=(x*w)(t)=\displaystyle\sum_{a=-\infty}^{\infty}x(a)\omega(t-a) s(t)=(x∗w)(t)=a=−∞∑∞x(a)ω(t−a)
而在机器学习的应用中,输入通常是多维数组的数据,而核通常是由学习算法优化得到的多维数组的参数。我们把这些多维数组叫做张量(Tensor)。因为在输入与核中的每一个元素都必须明确地分开存储,我们通常假设在存储了数值的有限点集之外,这些函数的值都为0。
我们经常会需要一次在多个维度上进行卷积计算。例如如果将一张二维的图像 I I I作为输入,我们也许也想要使用一个二维的核 K K K。
S ( i , j ) = ( I ∗ K ) ( i , j ) = ∑ m ∑ n I ( m , n ) K ( i − m , j − n ) S(i,j)=(I*K)(i,j)=\displaystyle\sum_m\displaystyle\sum_nI(m,n)K(i-m,j-n) S(i,j)=(I∗K)(i,j)=m∑n∑I(m,n)K(i−m,j−n),也可以等价地表示为 S ( i , j ) = ( K ∗ I ) ( i , j ) = ∑ m ∑ n I ( i − m , j − n ) K ( m , n ) S(i,j)=(K*I)(i,j)=\displaystyle\sum_m\displaystyle\sum_nI(i-m,j-n)K(m,n) S(i,j)=(K∗I)(i,j)=m∑n∑I(i−m,j−n)K(m,n)
上述的公式也很好理解, I I I代表输入矩阵, K K K代表卷积核矩阵,还记得当我们进行卷积运算的时候,我们需要先将卷积核矩阵进行一次翻转(flip) ,因此m和n增大的话,输入矩阵索引是对应增大,但是相对的卷积核矩阵索引会变小。在许多神经网络库里会实现一个相关的函数,称为互相关函数, 这个函数则不会对卷积核翻转,因此公式是: S ( i , j ) = ( I ∗ K ) ( i , j ) = ∑ m ∑ n I ( i + m , j + n ) K ( m , n ) S(i,j)=(I*K)(i,j)=\displaystyle\sum_m\displaystyle\sum_nI(i+m,j+n)K(m,n) S(i,j)=(I∗K)(i,j)=m∑n∑I(i+m,j+n)K(m,n)。不过一般而言我们都会特别指明这个核是否进行了翻转。卷积算法通常与其他的函数一起使用,无论卷积运算是否对它的核进行了翻转,这些函数的组合通常是不可交换的。
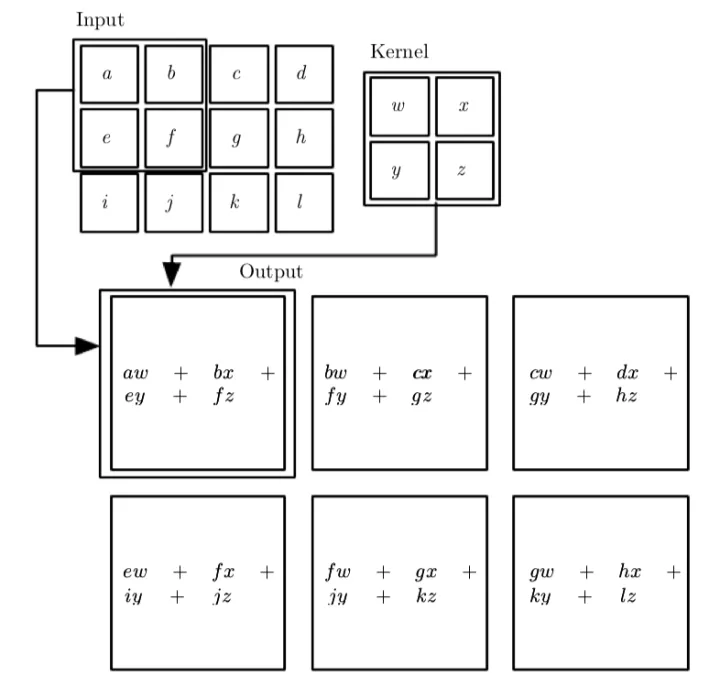
上图则是一个未翻转的卷积核计算的例子。
我们将上述的输出矩阵称为Toeplitz 矩阵,任何一个使用矩阵乘法但是并不依赖矩阵结构的特殊性质的神经网络算法,都适用于卷积运算。
动机
卷积运算通过三个重要的思想来帮助改进机器学习系统:稀疏交互,参数共享,等变表示,另外卷积还提供了一种处理大小可变的输入的方法。
稀疏交互
在传统的神经网络中,使用矩阵乘法来建立输入与输出的连接关系,参数矩阵中的每一个单独的参数都描述了一个输入单元与一个输出单元之间的交互,也就意味着传统的神经网络中每一个输出单元与输入单元都产生交互,如下图所示。
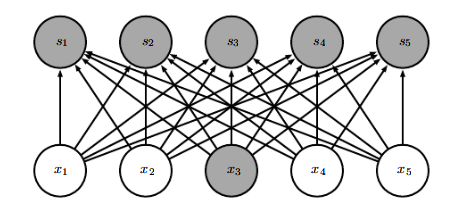
而卷积网络具有是稀疏交互或者稀疏权重的特征,这就意味着我们可以通过控制卷积核的大小来实现简化神经网络的连接。例如一个包含了成千上万像素点的图像,我们可以通过只占用几十个到上百个像素点的卷积核运算来检测一些小的具有意义的特征——例如图像的边缘检测。这意味着我们所需连接更少了,所需存储的连接的参数更少了,不仅减少了模型的存储需求,还提高了它的统计效率。对于m个输入和n个输出,矩阵乘法需要m×n个参数,也就代表了复杂度 O ( m × n ) O(m×n) O(m×n),但是如果仅需k个连接,也就是核宽度为k的卷积,那么所需复杂度就为 O ( k × n ) O(k×n) O(k×n),如下图所示:
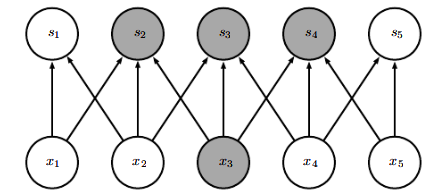
注意我们在上图中标为灰色的单元,在第一幅图中代表了 x 3 x_3 x3的输入和 s 1 . . . s 5 s_1...s_5 s1...s5都相关,但是使用了卷积之后 x 3 x_3 x3的输入只和 s 2 , s 3 , s 4 s_2,s_3,s_4 s2,s3,s4相关了,此时连接变得稀疏,相当于下图,其中橙色区块代表卷积核。
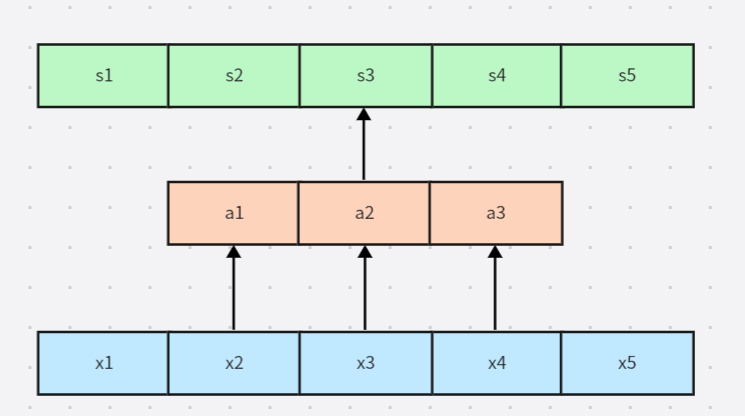
其中我们可以将 x 2 , x 3 , x 4 x_2,x_3,x_4 x2,x3,x4称为 s 3 s_3 s3的接受域
在卷积网络中,处于网络深层的单元可以与绝大部分输入是间接交互,这允许网络可以通过只描述稀疏交互的基石来高效的描述多个变量的复杂交互,如下图所示(接受域一清二楚):
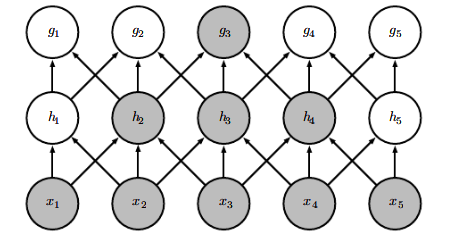
参数共享
参数共享是指在一个模型的多个函数中使用相同的参数,在传统的神经网络中,计算一层的输出时,权重矩阵的每一个元素都只使用一次。而在卷积网络中,由于卷积核不断在滑动,因此我们可以将卷积核的每一个元素都作用在输入的每一位置上,保证了我们只需要学习一个参数集合而非对每一个位置学习一个单独的参数集合,将模型的存储需求降低到了k个参数。因此,卷积在存储需求和统计效率方面极大地优于稠密矩阵的乘法运算,下图演示了参数共享是如何实现的:
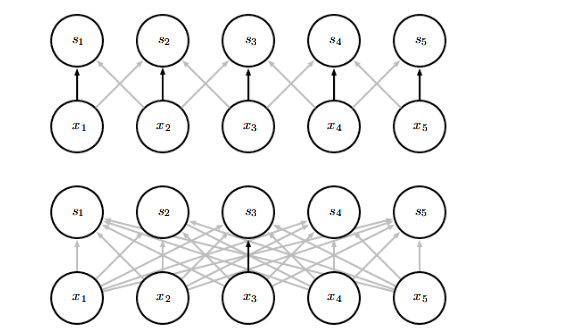
黑色箭头表示了在上下两个不同的模型中使用了特殊参数的连接。在上面的卷积神经网络模型中所有输入的中间元素共享一个参数。而下图中的普通神经网络模型每个输入的连接只能使用唯一的参数。
等变表示
对于卷积,参数共享的特殊形式使得神经网络层具有对平移等变的性质,如果一个函数满足输入改变,那么输出也可以同样的方式进行改变,我们就称其为等变。
特别的,如果hanshu f ( x ) f(x) f(x)与 g ( x ) g(x) g(x)满足 f ( g ( x ) ) = g ( f ( x ) ) f(g(x))=g(f(x)) f(g(x))=g(f(x)),我们就称 f ( x ) f(x) f(x)对于变换 g g g具有等变性。
举一个例子:例如我们对图像函数 I I I进行右移一位像素的变换,随后再对输入进行卷积。其结果与先对输入进行卷积,再对输出进行右移一位像素的变换是等价的。
这个性质意味着,我们处理时间序列数据时,通过卷积可以得到一个由输入中出现不同特征的时刻所组成的时间轴。如果我们把输入中的一个事件向后延时,在输出中仍然会有完全相同的表示,只是输出结果在时间上延后了。也就是对输入的延后可以对应实现输出延后。而在图像处理时,对输入的位移也可以实现对输出的相同位移。
除了上述我们说的位移操作之外,卷积对其他的一些变换并不是天然等变的,例如图像的放缩或者旋转变换,需要一些其他的机制来处理。
池化
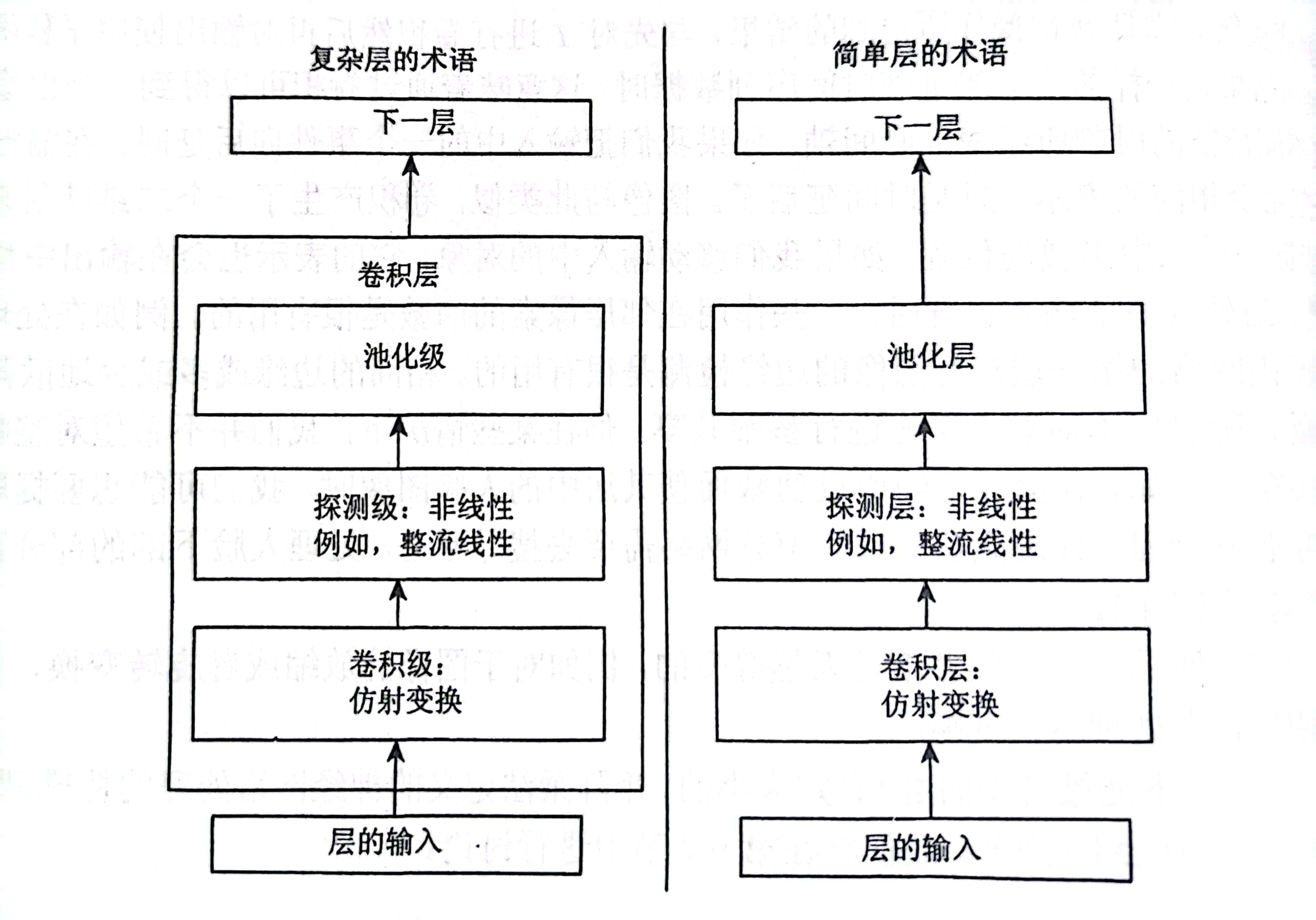
上图是卷积网络中的一个典型层,其包含三级。我们来看左图复杂层对神经网络的描述,在第一级卷积级中,这一层并行的计算多个卷积,产生一组线性激活相应。第二级探测级中,每一个线性激活响应将会通过一个非线性的激活函数,例如ReLU。在第三级池化级中,我们使用池化函数来进一步调整这一层的输出。
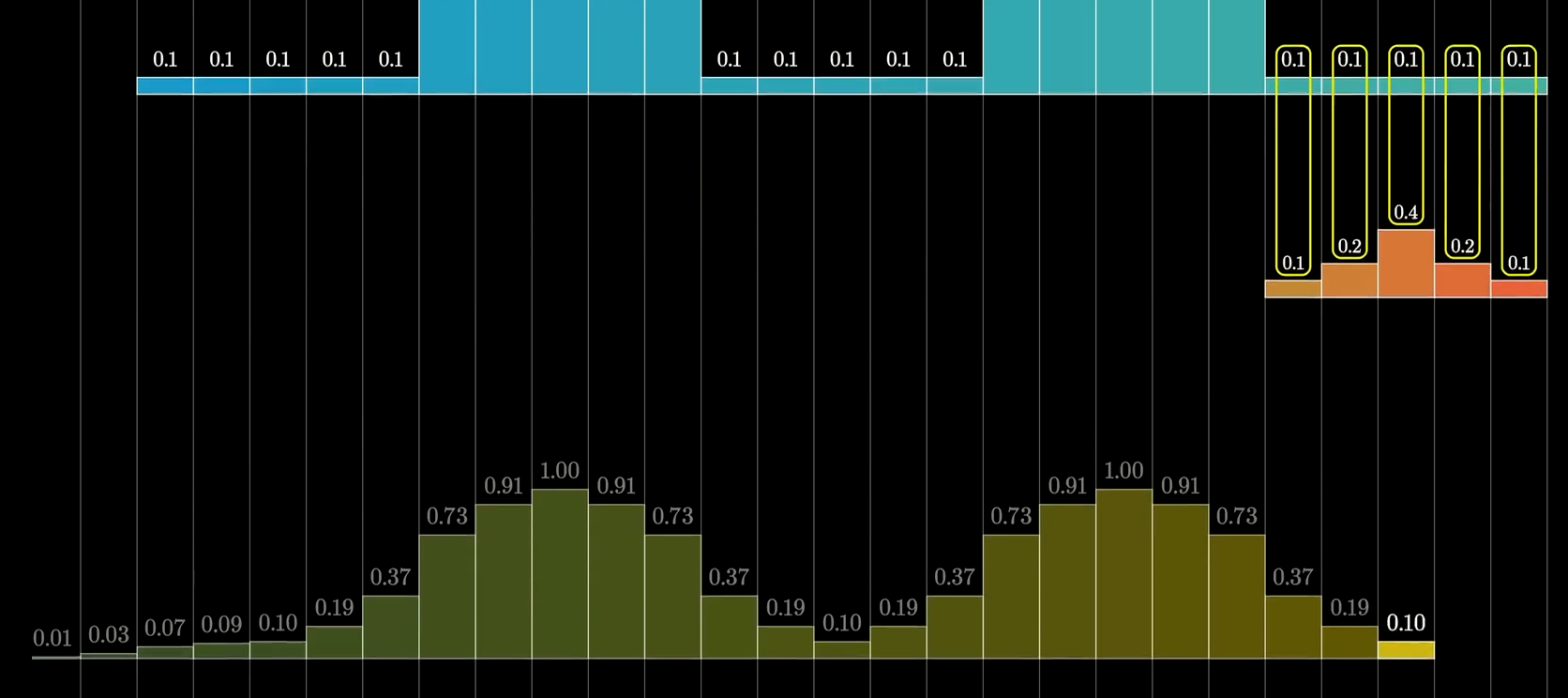
池化函数使用某一位置的相邻输出的总体统计特征来代替网络在该位置的输出,也就是一种压缩方法。例如最大池化函数,我们将输出分为不同的区块,选取区块中的最大值来代表其相邻区域的输出,如下图所示:
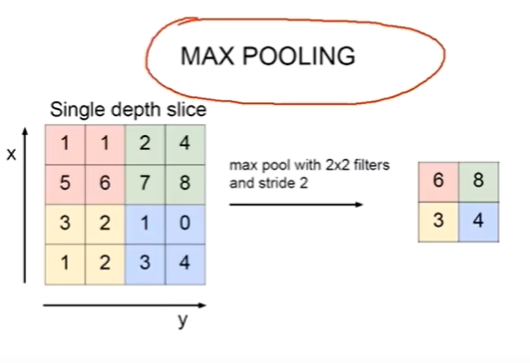
也存在其他的常用池化方法,例如平均值选取,欧几里得距离范数以及基于距中心像素距离的加权平均函数。
不管我们采用什么样的池化函数,当输入作出少量平移时,池化能够帮助输入的表示近似不变。平移的不变性是指当我们对输入进行少量平移时,经过池化函数后的大多数输出并不会发生改变。例如下图的例子说明了这是怎么实现的:
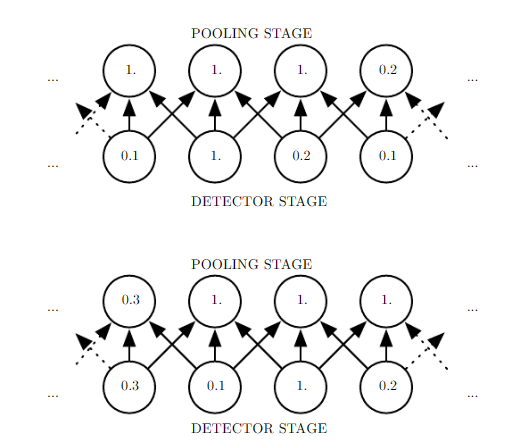
上图展示了池化的不变性,下面一行在探测级上给出了非线性的输出(例如ReLU整流后的结果),上面一行代表了最大池化的输出,每个池的宽度为三个像素并且池化区域的步幅为一个像素,池化层选取了输入中的最大值作为输出结果。
在下图中,我们将探测级的数据整体向右移动一个像素,我们可以看到实际上池化级的输出也向右移动了一个像素,这是因为最大池化单元只对周围的最大值比较敏感,而非对精确的位置。
局部平移不变性是一个很有用的性质,尤其是当我们关心某个特征是否出现而不关心它出现的具体位置时。 例如当我们需要判定一张图像中是否包含人脸时,我们并不需要知道眼睛的精确像素位置,我们只需要知道有一只眼睛在脸的左边,有一只在右边就行了。但在其他的一些领域,保存特征的具体位置很重要(通常是位置相关的一些要素)。
使用池化可以看作增加了一个无限强的先验:即这一层学得的函数必须具有对少量平移的不变性。当这个假设成立时,我们就可以应用局部平移不变性来极大地提高网络的统计效率。
对空间区域进行池化产生了平移不变性,但当我们对分离参数的卷积的输出进行池化时,特征能够学得应该对于哪种变换具有不变性。如下图所示:
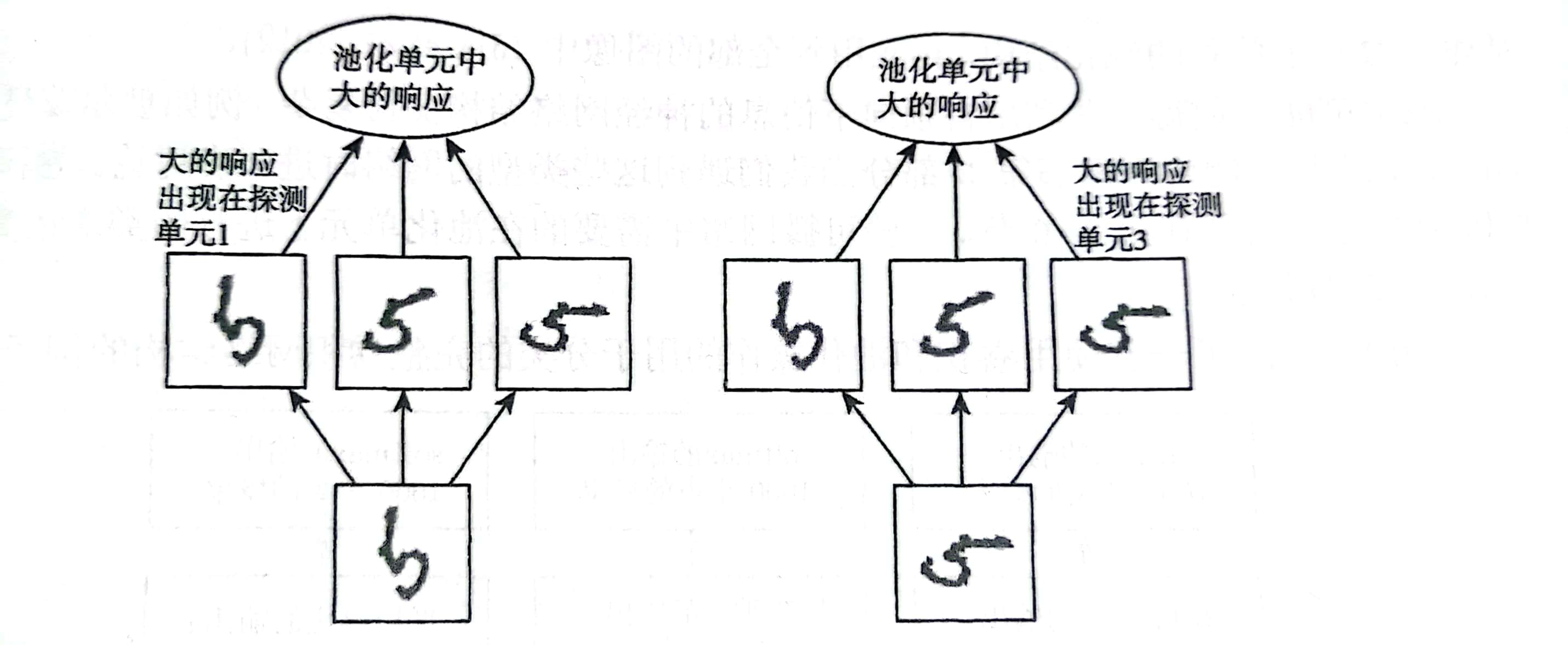
上图是一个学习不变性的示例。使用分离的参数学得多个特征,再使用池化单元进行池化,可以学得对输入的某些变换的不变性。在这里我们使用三个学得的过滤器和一个最大池化单元可以学得对旋转变换的不变性。这三个过滤器都旨在检测手写的数字5,但是每个过滤去都尝试匹配不同方向的5。
当输入中出现5时,相应的过滤器会匹配它并且在探测单元中引起大的激活。而在最大池化单元中就会选择最大的激活。因此如图所示的左右示例,面对两种不同的输入,虽然导致不同探测单元被激活,但对于池化单元的影响是大致相同的。
对于平移变换,池化总是具有不变性。这种多通道的探测方法在学习其他变换(例如上述的旋转变换)时是必要的。
由于池化综合了全部邻居的反馈,因此池化单元可以少于探测单元。我们可以通过综合池化区域的 k k k个像素的统计特征而不是单个像素来实现。(类似于卷积层,对于n个输入可以稀疏交互,不过单元更少)如下图所示:
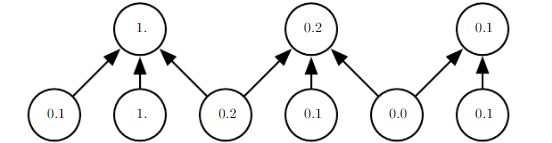
上述例子使用最大池化,池的宽度为3且步幅为2。这使得表示的大小减少了一般,减轻了下一层的计算和统计负担,因此我们说池化是一种简化方法。池化可以通过调整池化区域的偏置大小,来控制通过池化层得到的固定大小的输出。无论给予池化层多大的输入值,总能够得到固定大小的池化输出,因此池化对于将不同大小的输入处理为同一大小的输出具有重要的作用。

上面给出的是一些使用了卷积和池化操作的用于分类的完整卷积网络结构的例子。请大家注意每个模型的第六层往后的结构。第六层是全连接权重层,是池化输出和前馈网络输入的连接部分。
左图是处理固定大小图像的卷积网络,最终卷积的输出(第六层)——即卷积特征映射的张量被重新变形以展平空间维度(16384个单元)再作为输入值,其输入的单元softmax是一个普通的前馈网络分类器。其限制在于输入图像的大小是固定的。
中间是一个处理大小可变的图像的卷积网络,在第五层通过卷积池化,对于任意的输入大小,我们都能得到一个特定大小的网格输出3×3×64,最后为卷积与前馈网络输入层的全连接部分(第六层)提供一个576单元的向量输出。也就是对于任意输入大小我们都可以得到相同大小的卷积层输出。
右图在卷积与前馈网络输入层(第六层)并没有任何全连接权重。是直接应用了卷积层的输出作为前馈网络的输入,由于前馈网络需要分出1000个类别,相对的卷积层为每个类输出了一个特征映射,因此得到了16×16×1000。该模型可能用于学习每个类出现在每个空间位置的可能性的映射。
卷积和池化作为一种无限强的先验
先验概率分布是一个模型基于参数的概率分布,它刻画了我们在看到数据之前认为什么样的模型是合理的信念,即概率 P ( A ) P(A) P(A)。
这里需要提到一点:
- 方差表示随机变量的变化程度
- 熵表示随机变量的不确定程度
简单理解的话方差和熵具有很强的正相关性。
先验被认为是强或者弱取决于先验中概率密度的集中程度。弱先验具有较高的熵值,例如方差较大的高斯分布。这样的先验允许数据对于参数的改变相对自由,参数影响较小。
而强先验具有较低的熵值,例如方差较小的高斯分布。这样的先验在决定参数最终取值时起到更加积极的作用。
而使用卷积和池化这样的一种无限强的先验,则需要我们对参数作出较大的限制,例如对一些参数的概率置0并且完全禁止对这些参数赋值,无论数据对于这些参数的值给出了多大的支持。
我们可以把卷积层的使用当作对网络中的一层的参数引入了无限强的先验——要求该层的一个隐藏单元的权重必须和其邻居的权重相同(参数共享)以保证平移的不变性。而除了处于隐藏单元的接受域内的权重以外,其余的权重都为0。