目录
1.多项式微分与积分
1.1 微分
- 函数f(x)导数写为:F'(x)或者
- 函数f(x)关于x的变化率
f (x0) 表示点x0处曲线相切的直线的系数。

1.2 多项式微分
对于一个多项式: 来说,其微分多项式为:
1.3 如何正确的使用Matlab?
1.3.1 Matlab表达多项式
在上式中,我们用Matlab应该怎么进行表示(多项式在Matlab中被表示为行向量)
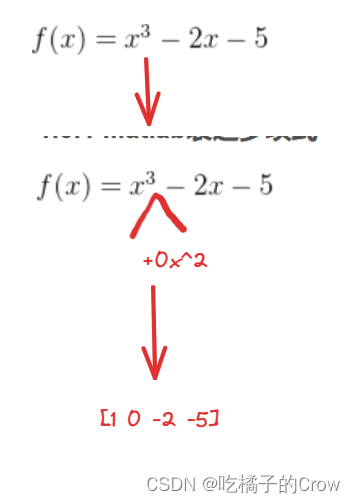
>> p=[1 0 -2 -5]
p =
1 0 -2 -51.3.2 polyval() 多项式求值
语法:y=polyval(p,x)
y= polyval(p,x) 计算多项式 p 在 x 的每个点处的值。参数 p 是长度为 n+1 的向量,其元素是 n 次多项式的系数(降幂排序):
示例1:
计算多项式 p(x)=3x^2+2x+1在点 x=5、7 、9 处的值。
>> p = [3 2 1];
x = [5 7 9];
y = polyval(p,x)
y =
86 162 262
示例2:
对该多项式进行画图求值
>> a = [9,-5,3,7]; x = -2:0.01:5;
f = polyval(a,x);
plot(x,f,'LineWidth', 2);%设置线条粗度
xlabel('x轴'); ylabel('f(x)');%设置xy轴名称
set(gca, 'FontSize', 14)%设置字体大小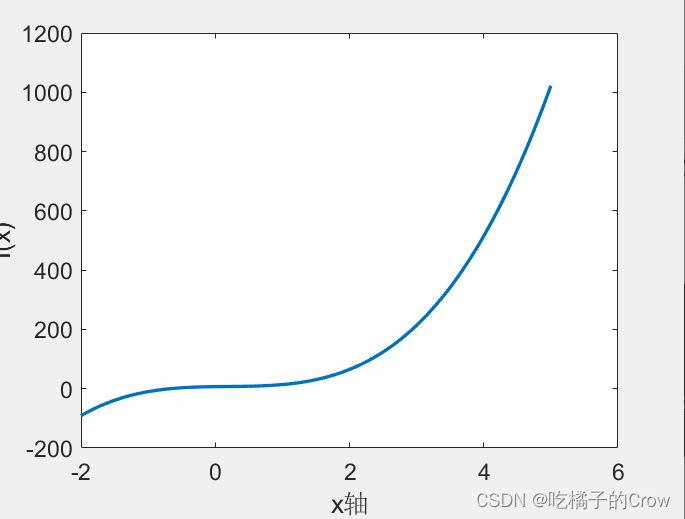
1.3.3 polyder()多项式微分
语法一:k=polyder(p)
k=polyder(p)返回的p中的系数表示的多项式的导数
示例:
创建一个向量来表示多项式 p(x)=3x^5−2x^3+x+5。
p = [3 0 -2 0 1 5]; 使用polyder对多项式进行求导,结果为:
q = polyder(p)
q = 1×5
15 0 -6 0 1 语法二:k= polyder(a,b) 返回多项式 a 和 b 的乘积的导数
示例:
创建两个向量来表示多项式 a(x)=x^4−2x^3+11 和 b(x)=x^2−10x+15。
a = [1 -2 0 0 11];
b = [1 -10 15];q = polyder(a,b)
q = 1×6
6 -60 140 -90 22 -110最后的结果为:
语法三:[q,d] = polyder(a,b) 返回多项式 a 和 b 的商的导数
示例:
创建两个向量来表示商中的多项式
p = [1 0 -3 0 -1];
v = [1 4];[q,d] = polyder(p,v)
q = 1×5
3 16 -3 -24 1
d = 1×3
1 8 16结果为:
1.4 多项式积分
对于一个多项式:
积分多项式为:
1.4.1 如何正确表达
1.4.2 polyint() 多项式积分
语法:q=polyint(p,k) 如果只有的一个参数p,默认k是0,使用积分常量k返回p中的系数所表示的多项积分
示例:
对两个多项式的乘积求积分
- 创建向量来表示多项式
p = [1 0 -1 0 0 1];
v = [1 0 1];- 多项式相乘,并使用积分常量k=3对所生成的表达式求积分
k = 3;
q = polyint(conv(p,v),k)
q = 1×9
0.1250 0 0 0 -0.2500 0.3333 0 1.0000 3.0000- 通过在积分范围上计算q来求解I的值
a = 0;
b = 2;
I = diff(polyval(q,[a b]))
I =
32.66672.数值的微分与积分
2.1 数值微分
- 最简单的方法:有限差分近似法
- 计算x附近的割线
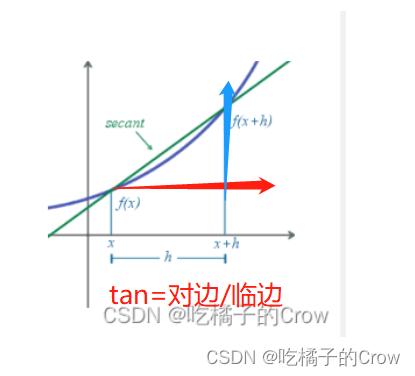
2.2 diff() 计算差值
diff() 计算向量中相邻元素之间的差值
x = [1 2 5 2 1];
diff(x)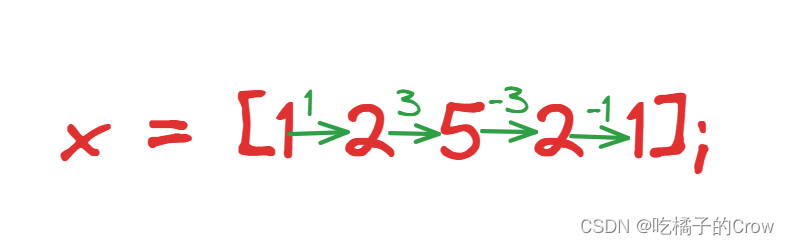
>> x = [1 2 5 2 1];
diff(x)
ans =
1 3 -3 -1示例:
求出两点之间的斜率
>> x = [1 2]; y = [5 7];
slope = diff(y)./diff(x) %y的变化量/x的变化量
slope =
22.3 误差的准确性
当
h=0.1、0.01、0.001s时误差有什么变化?
当h=0.1时:
>> x0 = pi/2; h = 0.1;
x = [x0 x0+h];
y = [sin(x0) sin(x0+h)];
m = diff(y)./diff(x)
m =
-0.0500当h=0.01时:
>> x0 = pi/2; h = 0.01;
x = [x0 x0+h];
y = [sin(x0) sin(x0+h)];
m = diff(y)./diff(x)
m =
-0.0050当h=0.001时:
>>
x0 = pi/2; h = 0.001;
x = [x0 x0+h];
y = [sin(x0) sin(x0+h)];
m = diff(y)./diff(x)
m =
-5.0000e-04由分析得:所以当h->0时,误差越小
g = colormap(lines); hold on;
for i=1:4
x = 0:power(10, -i):pi;
y = sin(x); m = diff(y)./diff(x);
plot(x(1:end-1), m, 'Color', g(i,:));%每次微分,系数的个数少1
end
hold off;
set(gca, 'XLim', [0, pi/2]); set(gca, 'YLim', [0, 1.2]);
set(gca, 'FontSize', 18); set(gca, 'FontName', 'symbol');
set(gca, 'XTick', 0:pi/4:pi/2);
set(gca, 'XTickLabel', {'0', 'p/4', 'p/2'});
h = legend('h=0.1','h=0.01','h=0.001','h=0.0001');
set(h,'FontName', 'Times New Roman'); box on;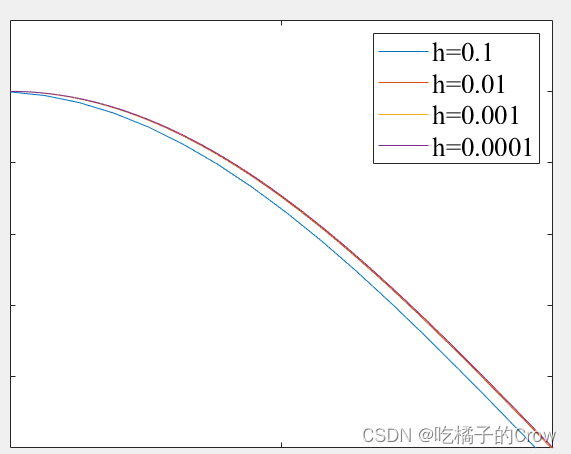
2.4 二阶、三阶导数
>> x = -2:0.005:2; y = x.^3;
m = diff(y)./diff(x);
m2 = diff(m)./diff(x(1:end-1));
plot(x,y,x(1:end-1),m,x(1:end-2),m2);%每次导数系数减1
xlabel('x', 'FontSize', 18);
ylabel('y', 'FontSize', 18);
legend('f(x) =x^3','f''(x)','f''''(x)');
set(gca, 'FontSize', 18);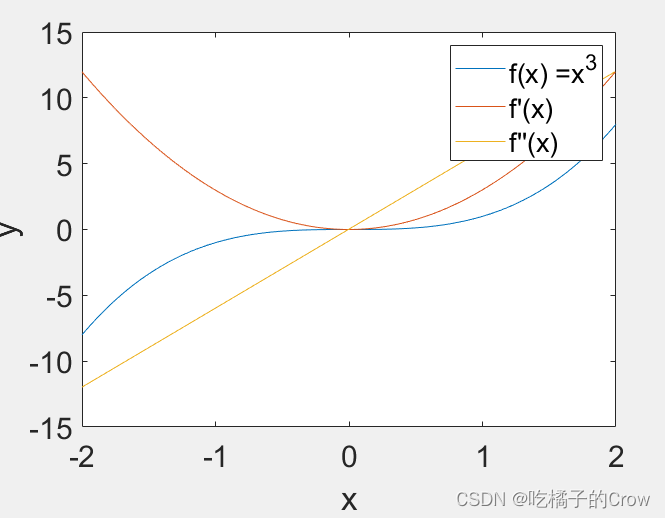
2.5 数值积分
- 求积法——用有限集点逼近积分
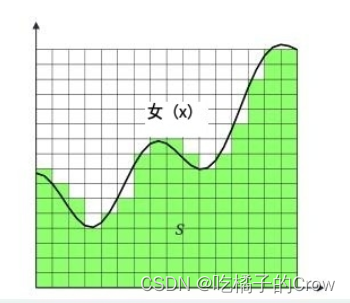
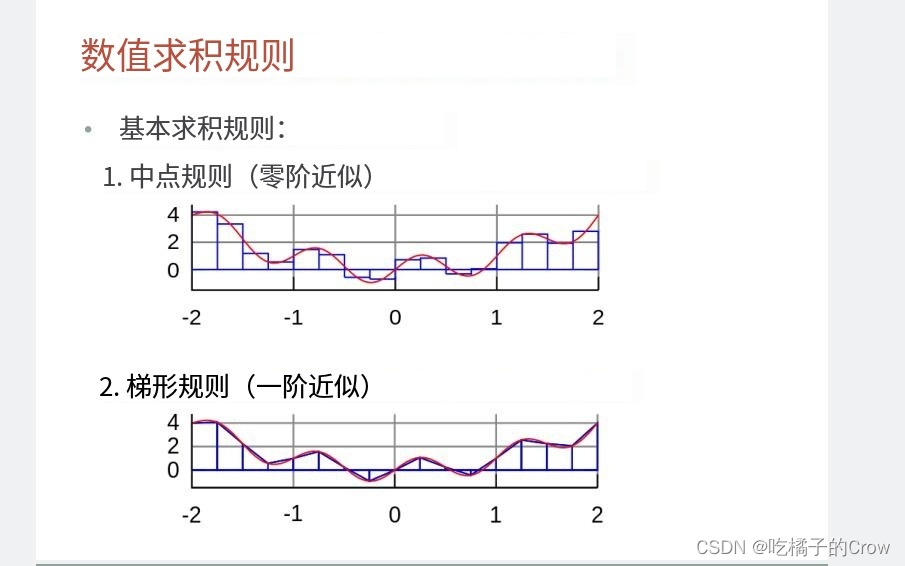
2.5.1中点规则
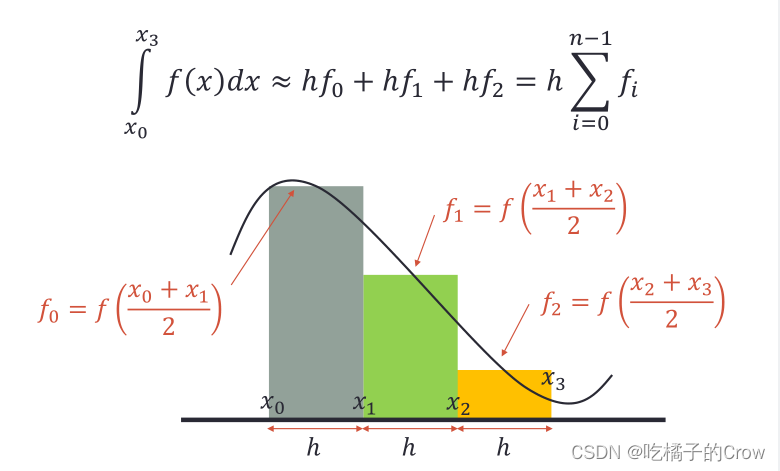
示例:
我们通过积分可以求得:
但是我们通过中点积分可得:
>> h = 0.05; x = 0:h:2;
midpoint = (x(1:end-1)+x(2:end))./2;
y = 4*midpoint.^3;
s = sum(h*y)
s =
15.9950解释:
midpoint = (x(1:end-1)+x(2:end))./2;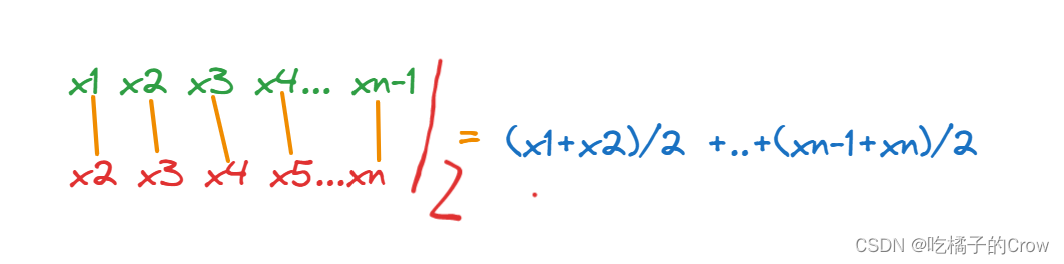
2.5.2 梯形规则(trapz)
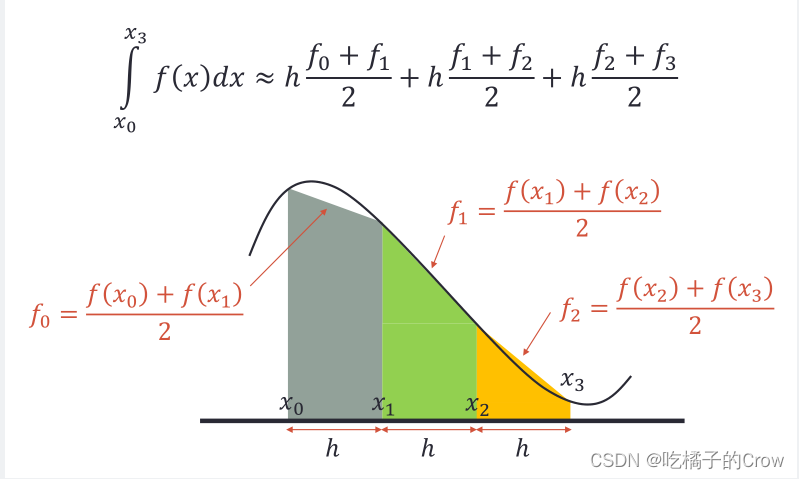
>> h = 0.05; x = 0:h:2; y = 4*x.^3;
s = h*trapz(y)
s =
16.0100我们也可以自定义该函数:
h = 0.05; x = 0:h:2; y = 4*x.^3;
trapezoid = (y(1:end-1)+y(2:end))/2;
s = h*sum(trapezoid)
s =
16.01002.5.3 辛普森积分法
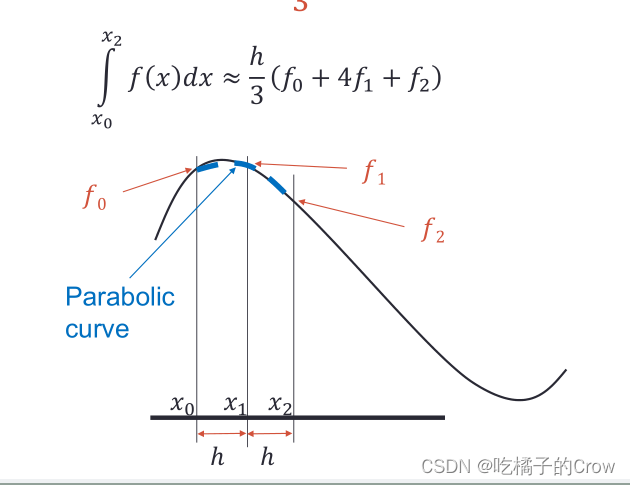
>> h = 0.05; x = 0:h:2; y = 4*x.^3;
s = h/3*(y(1)+2*sum(y(3:2:end-2))+...
4*sum(y(2:2:end))+y(end))
s =
162.5.4 三种积分方式比较
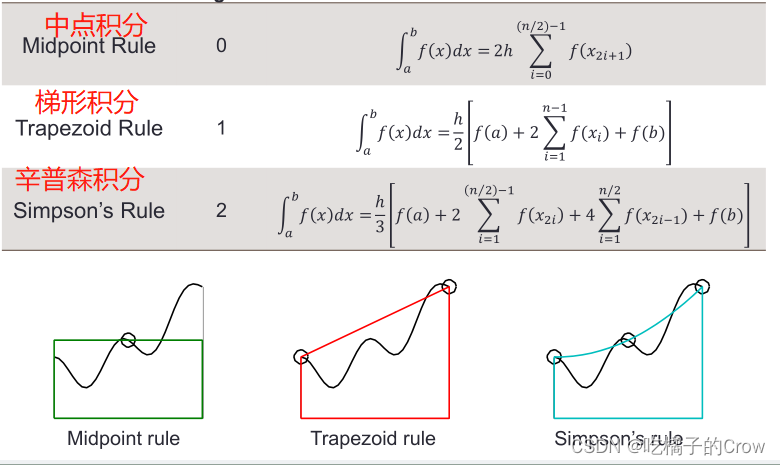
由分析易得: 辛普森积分法误差最小
3.函数句柄
函数句柄是一种存储指向函数的关联关系的Matlab数据类型,间接调用函数使您在调用函数时无需考虑调用位置,函数句柄的典型用法包括:
- 将一个函数传递到另一个函数(通常称为复合函数)
- 指定回调函数
- 构造以内联方式定义而非存储在程序文件(匿名函数)中的函数句柄
- 从主函数外调用局部函数
查看h是否是函数句柄
isa(h,'function_handle')3.1 创建函数句柄
通过在函数名称前添加一个 @ 符号来为函数创建句柄。
f = @myfunction;3.1.1 有参数的句柄函数
使用句柄调用函数的方式与直接调用函数一样,例如:
function y = computeSquare(x)
y = x.^2;
end创建句柄并调用该函数以计算 4 的平方。
f = @computeSquare;
a = 4;
b = f(a)
b =
163.1.2 无参数的句柄函数
如果该函数不需要任何输入,则您可以使用空括号调用该函数,例如:
h = @ones;
a = h()
a =
1
3.1.3 无参且无括号
如果不使用括号,则该赋值会创建另一个函数句柄。
a = h
a =
@ones3.2 匿名函数
您可以创建指向匿名函数的句柄。匿名函数是基于单行表达式的 MATLAB 函数,不需要程序文件。构造指向匿名函数的句柄,方法是定义 anonymous_function 函数主体,以及指向匿名函数 arglist 的以逗号分隔的输入参数列表。语法为:
h = @(arglist)anonymous_function例如,创建一个指向用于计算平方数的匿名函数的句柄 sqr,并使用其句柄调用该匿名函数。
sqr = @(n) n.^2;
x = sqr(3)
x =
93.3 错误示范
function [y] = xy_plot(input,x)
% xy_plot receives the handle of a function
% and plots that function of x
y = input(x); plot(x,y,'r--');
xlabel('x'); ylabel('function(x)');
end
>> xy_plot(sin,0:0.01:2*pi)
错误使用 sin
输入参数的数目不足。调用参数的时候,如果该参数也是一个函数,这个时候直接将函数当成参数输入进去是不妥的,会直接报错,这个时候我们就需要句柄
>>
xy_plot(@sin,0:0.01:2*pi)
ans =
列 1 至 11
0 0.0100 0.0200 0.0300 0.0400 0.0500 0.0600 0.0699 0.0799 0.0899 0.0998
列 12 至 22
0.1098 0.1197 0.1296 0.1395 0.1494 0.1593 0.1692 0.1790 0.1889 0.1987 0.2085
列 23 至 33
0.2182 0.2280 0.2377 0.2474 0.2571 0.2667 0.2764 0.2860 0.2955 0.3051 0.3146
...3.4 integral() 数值积分
3.4.1 一级积分
我们通过句柄该怎么去解决呢?
>> y = @(x) 1./(x.^3-2*x-5);
integral(y,0,2)
ans =
-0.46053.4.2 integral2() 二级积分
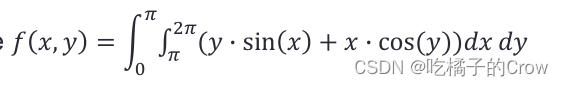
>> f = @(x,y) y.*sin(x)+x.*cos(y);
integral2(f,pi,2*pi,0,pi)
ans =
-9.86963.4.3 integral3() 三级积分
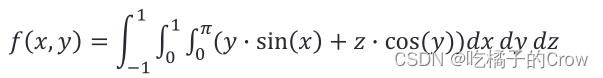
>> f = @(x,y,z) y.*sin(x)+z.*cos(y);
integral3(f,0,pi,0,1,-1,1)
ans =
2.0000