解微分方程算法主要用于微机距离保护中计算阻抗,其实解微分方程算法并非要解微分方程,而是利用电力线路的电压微分方程关系式,求解二元一次方程的未知数:短路故障线路电阻和线路电感,因此该算法确切地说是R-L串联模型算法。
该算法的前提条件是假设输电线路的分布电容可以忽略。当输电线路发生故障时,从故障点到保护安装处的线路可用电阻和电感串联电路来表示,下列微分方程式成立

式中和分别为故障点到保护安装处的线路正序电阻和正序电感,u和i分别为保护安装处采样到的电压和电流瞬时值。可见,已知采样电压和电流时,通过解(2-14)可求得和。
常规的距离保护的接线方式,对相间保护按0接线方式,例如AB相阻抗元件=,=-;对接地距离保护按零序补偿电流法,例如A相阻抗元件=,=十·3(为零序补偿系数)。在微机保护中,模拟量输入电路虽然不存在接线方式的问题,但采样计算后,代入式(2-14)的电压和电流应当用上述的接线方式,即相间故障时取,取一代入式(2-14)中的u和i;接地故障时取和+·3代入式(2-14)中的u和i,才能满足保护对接线方式的要求。所以式(2-14)是具有代表意义的微分方程式。由此可见,采样后式(2-14)中u、i和di/dt均是已知数,而未知数是和。如果在两个不同时刻和分别采样计算出u、i、di/dt,那么就可以得到两个

式中u和i的下标1和2分别表示两个测量时刻和。D表示为di/dt,即=di/dt,=di/dt。
那么从式(2-15)和(2-16)联合解的结果就可以求出未知数和,也就是可以求出短路线路阻抗Z=r+jx。这就是二元一次代数方程式求解短路线路阻抗的基本原理。
联立解以上两式可求得

在用计算机处理式(2-17)和式(2-18)时,电流的导数di/dt可用差分法计算,即取和。分别为两个相邻的采样瞬间的中间值,如图2-3所示,于是有近似式

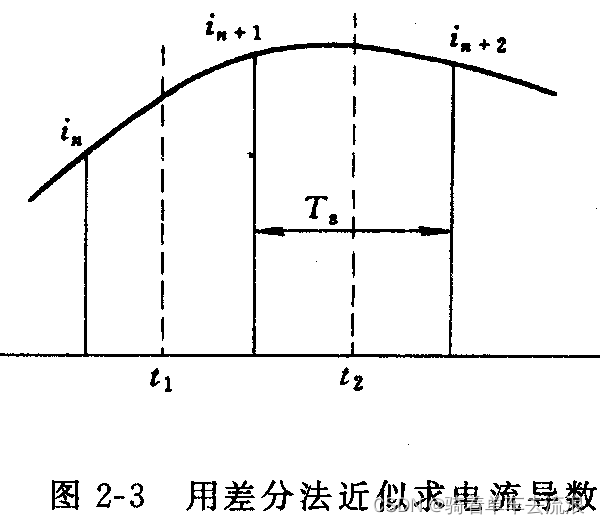
式中就是采样周期,可见只要采样点数N取得足够多,其电流的导数就可以计算得足够精确。
但是,值得注意的是式(2-14)已忽略了输电线路分布电容,实际上这种电容具有滤除电压电流中的非周期分量的作用。因此,忽略了这种分布电容的作用就会造成计算误差。为了克服由此带来的误差,在采样计算电压和电流前应经低通数字滤波(软件滤波)以消除非周期分量对计算误差的影响。为了证实以上的分析,研究人员对一条220kV线路采用微分方程法求解故障线路的短路距离的频率特性,见图2-4

由该图可以看出长100km左右的线路,由于分布电容不大,用低通数字滤波能消除忽略了分布电容造成的误差影响,其结果是故障线路的电压和电流的非周期分量低频成份对计算的R和L均无影响。这种R-L模型算法,不仅仅反映基频分量,而是在相当宽的一个低频段内都能适用。也就是说这种算法不需要用专用的滤波器去滤除非周期分量(滤除非同期分量需要延长时间),因为非周期分量中所含有的低频成份都是符合R-L模型算法的。因此使得这种只需附加低通滤波器的R-L算法较之其他需带通滤波器的算法延时时间短(因为低通滤波器的延时要比带通滤波器的延时短得多),从而使微机距离保护的动作速度加快。除此之外,这种R-L模型算法,还不受电网频率在事故时发生变化的影响,从而使得该算法能在较大的低频范围内准确地计算故障线路段的和