Runge-Kutta法解微分方程

连续问题，微分方程或偏微分方程一定能表示。比如疾病传染、新闻传播等。

离散问题，可以用差分方程或者类似于差分的算法。

方程

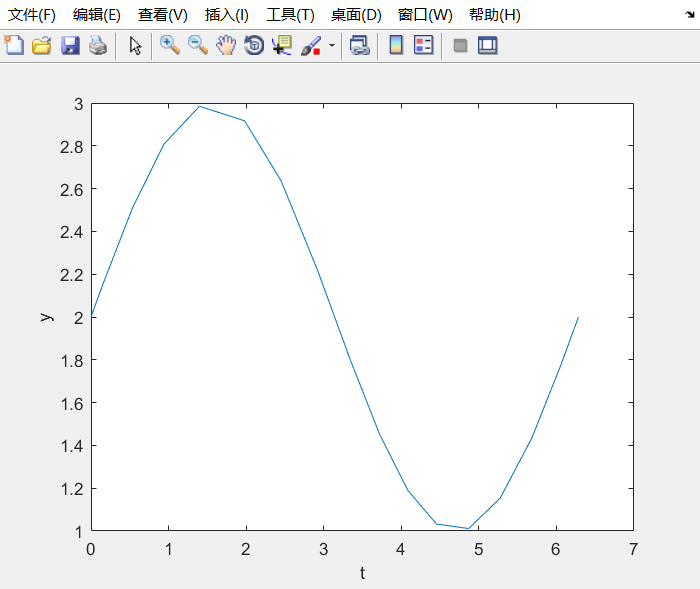
$y’=cos t$

代码

1 2 3 4 5 6 7 8 9

clear,clc; f = @(t,y) cos(t); tspan = [0,2*pi]; % 时间t范围 y0 = 2; % y的初值，用来处理积分得到的C [t,y] = ode23(f,tspan,y0); % 注意调用格式 plot(t,y); xlabel('t'); ylabel('y');

@表示句柄，当把一个函数作为参数传给另外一个函数，这时候必须要用句柄。这里是把函数f传给函数ode23。

结果

高阶微分方程求解

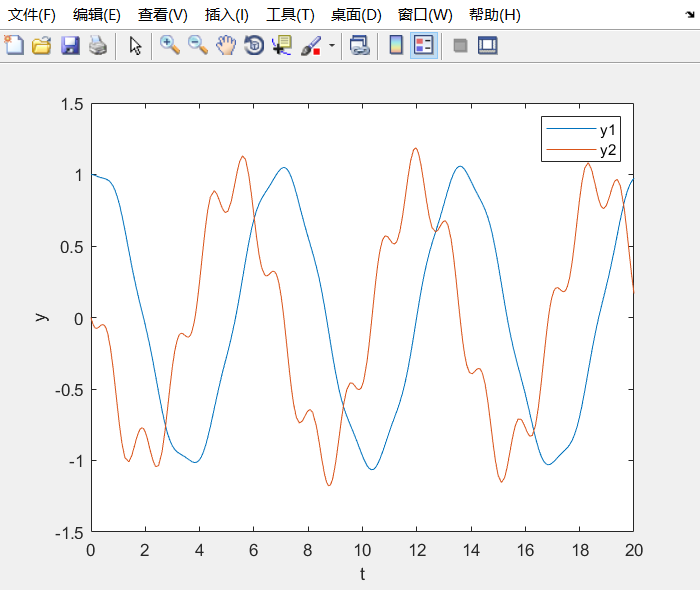
方程

$begin{equation}
left{
begin{array}{r1}
y’’=-sin y+sin 5t\
y(0)=1\
y’(0)=0\
end{array}
right.
end{equation}$

可以将该高阶微分方程转化为两个一阶的微分方程：$begin{equation}
left{
begin{array}{r1}
y_1=y\
y_2=y’\
y’_1=y_2\
y’_2=-sin y_1+sin 5t\
y_1(0)=1\
y_2(0)=0\
end{array}
right.
end{equation}$

代码

1 2 3 4 5 6 7 8 9 10

clear,clc; f = @(t, y) [ y(2); -sin( y(1) ) + sin( 5*t ) ]; % 两个参数分别是y1和y2的导数 tspan = [ 0, 20 ]; % 时间t范围 y0 = [ 1; 0 ]; % 初值，分别对应y1，y2的初值 [t, y] = ode23(f, tspan, y0); % 注意调用格式 plot(t,y); xlabel('t'); ylabel('y'); legend('y1','y2');

结果

​

作者：@臭咸鱼

本文为作者原创，转载请注明出处：https://chouxianyu.github.io

欢迎讨论和交流!

原文:大专栏  Runge-Kutta法解微分方程