- 定义:高维数据转化为低维数据的过程,在此过程中可能会舍弃原有数据、创造新的变量
- 作用:是数据维数压缩,尽可能降低原数据的维数(复杂度),损失少量信息。
- 应用:回归分析或者聚类分析当中(非监督学习算法)
- 降维是指在某些限定条件下,降低随机变量(特征)个数,得到一组“不相关”主变量的过程。
原理推导
在一个二维平面内

下图左一是上述点在特征2方向上的映射(扔掉特征1属性),右一是点在特征1方向的映射(扔掉特征2属性)。右一点和点的距离更为稀疏,差异更大,更有区分度。如果让选择一种方案把上述二维的数据降到一维,则右的方案更合理。
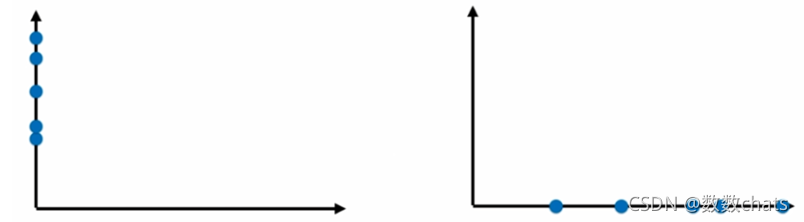
更好的解决方案,将所有的点映射到一根直线,整体跟原来的分布并没有太大的差距,且所有的点都存在一根斜轴上,也更加趋近原来点的分布情况。
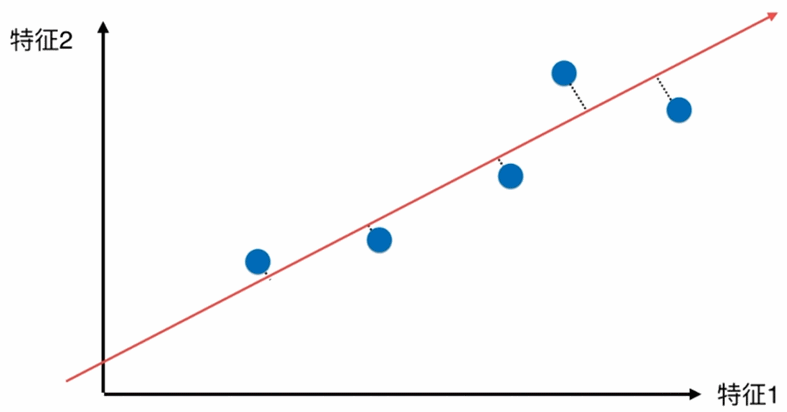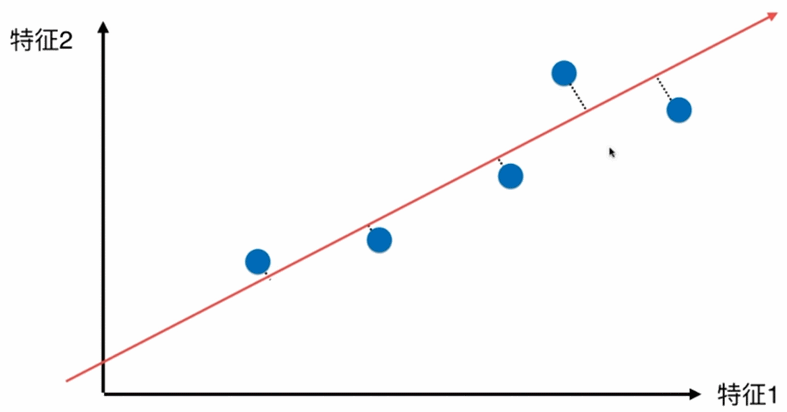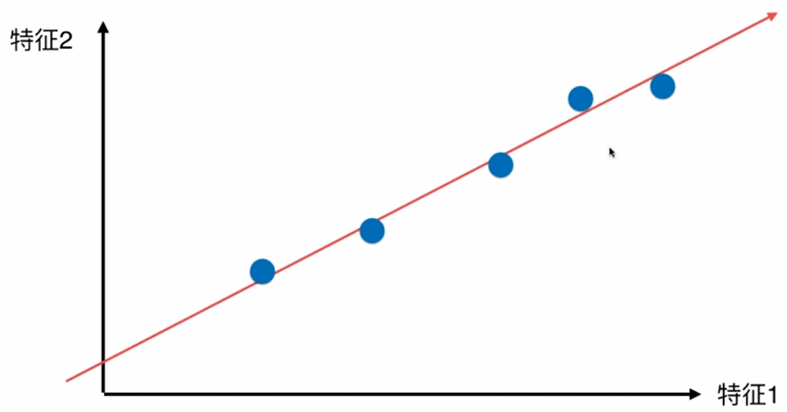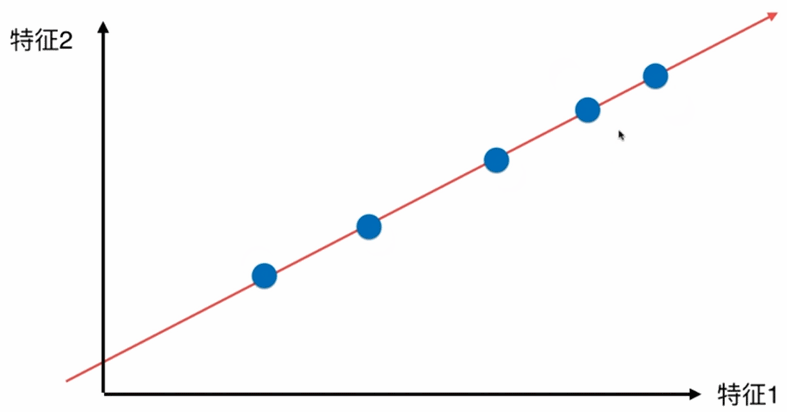
如何找到让这个样本间间距最大的轴
可以用方差定义样本间的间距: V a r ( x ) = 1 m ∑ i = 1 m ( x i − x ‾ ) 2 Var(x)=\frac{1}{m}\displaystyle \sum_{i=1}^m(x_i-\overline{x})^2 Var(x)=m1i=1∑m(xi−x)2
那么问题就转化为找到一个轴,使得样本空间的所有点映射到这个轴后,方差最大
第一步:将样例的均值归为0(demean)-----将坐标轴进行移动,使得样本在每个维度均值为0,则方差的公式由 V a r ( x ) = 1 m ∑ i = 1 m ( x i − x ‾ ) 2 Var(x)=\frac{1}{m}\displaystyle \sum_{i=1}^m(x_i-\overline{x})^2 Var(x)=m1i=1∑m(xi−x)2 变为 V a r ( x ) = 1 m ∑ i = 1 m ( x i ) 2 Var(x)=\frac{1}{m}\displaystyle \sum_{i=1}^m(x_i)^2 Var(x)=m1i=1∑m(xi)2
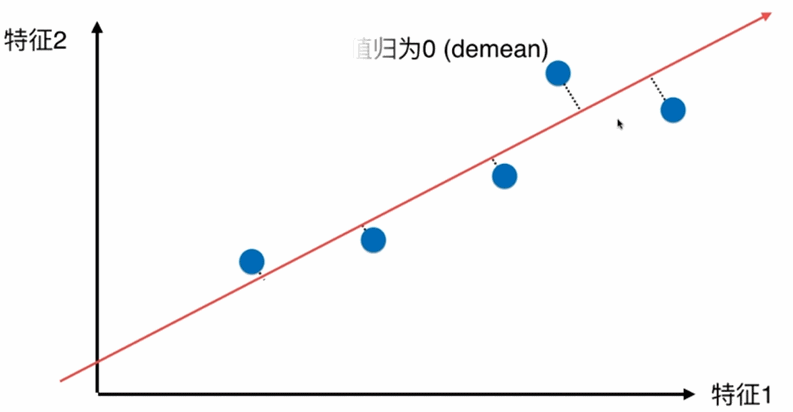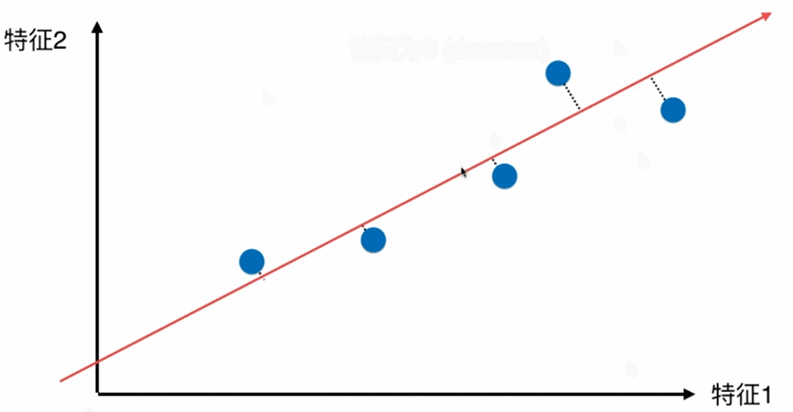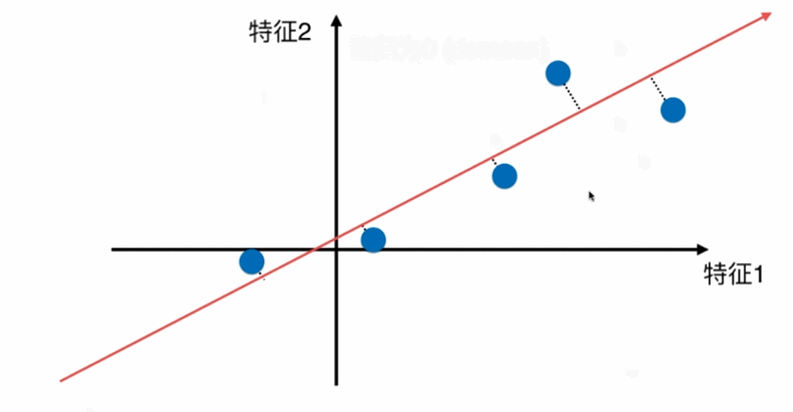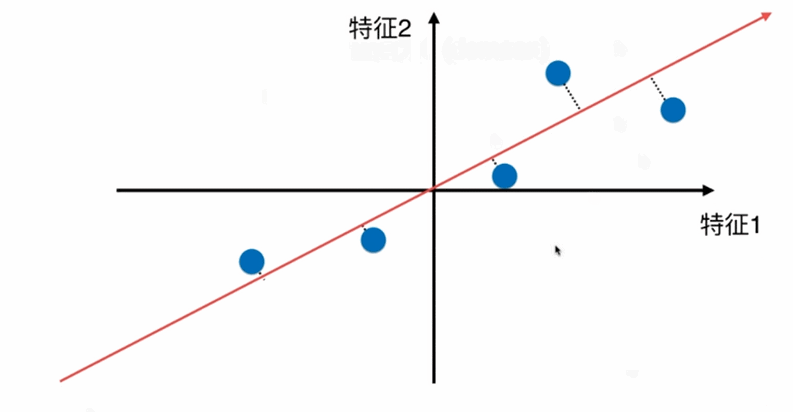
即对所有的样本进行demean处理
求一个轴的方向 w = ( w 1 , w 2 ) w=(w_1,w_2) w=(w1,w2), 使得所有的样本,映射到w以后,有:
V a r ( X p r o j e c t ) = 1 m ∑ i = 1 m ∥ X p r o j e c t ( i ) − X ‾ p r o j e c t ∥ 2 Var(X_{project})=\frac{1}{m}\displaystyle \sum_{i=1}^m\lVert X_{project}^{(i)}-\overline{X}_{project}\rVert ^2 Var(Xproject)=m1i=1∑m∥Xproject(i)−Xproject∥2 最大
又 X ‾ p r o j e c t = 0 \overline{X}_{project}=0 Xproject=0 则变为求 V a r ( X p r o j e c t ) = 1 m ∑ i = 1 m ∥ X p r o j e c t ( i ) ∥ 2 Var(X_{project})=\frac{1}{m}\displaystyle \sum_{i=1}^m\lVert X_{project}^{(i)}\rVert ^2 Var(Xproject)=m1i=1∑m∥Xproject(i)∥2 最大
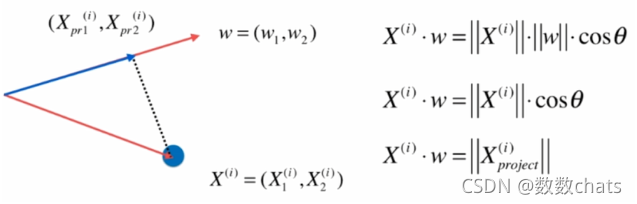
由上述推导( ∥ w ∥ = 1 \lVert w \rVert=1 ∥w∥=1) 转化为求 V a r ( X p r o j e c t ) = 1 m ∑ i = 1 m ( X ( i ) ⋅ w ) 2 Var(X_{project})=\frac{1}{m}\displaystyle \sum_{i=1}^m (X^{(i)}\cdot w)^2 Var(Xproject)=m1i=1∑m(X(i)⋅w)2 最大
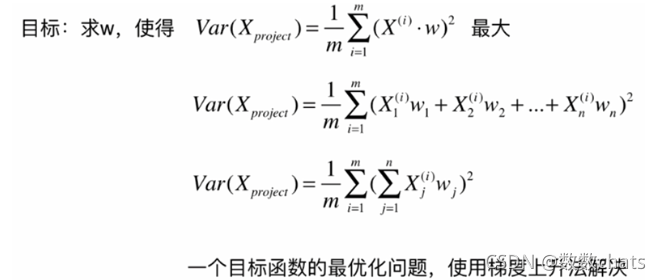

代码实现
import numpy as np
import matplotlib.pyplot as plt
X=np.empty((100,2))
X[:,0]=np.random.uniform(0,100,size=100)
X[:,1]=0.75*X[:,0]+3+np.random.normal(0,10,size=100)
plt.scatter(X[:,0],X[:,1])
plt.show()
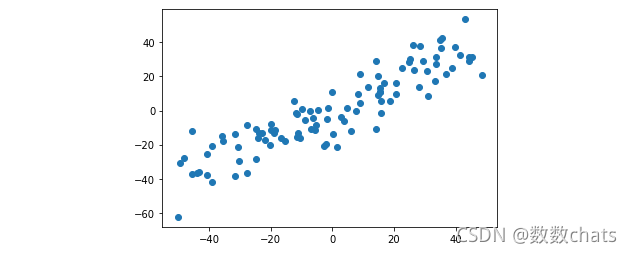
#demean
def demean(X):
return X-np.mean(X,axis=0)
X_demean=demean(X)
plt.scatter(X_demean[:,0],X_demean[:,1])
plt.show()
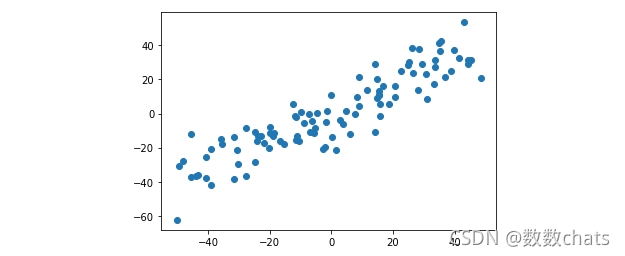
#demean后,每个特征方向上的均值几乎为0
np.mean(X_demean[:,0])
np.mean(X_demean[:,1])
#梯度上升法求主成分
#目标函数
def f(w,X):
return np.sum((X.dot(w)**2))/len(X)
#梯度函数
def df_math(w,X):
return X.T.dot(X.dot(w))*2/len(X)
# 验证梯度求解是否正确,使用梯度调试方法:
def df_debug(w,X,epsilon=0.0001):
res=np.empty(len(w))
# 对于每个梯度,求值
for i in range(len(w)):
w_1=w.copy()
w_1[i]+=epsilon
w_2=w.copy()
w_2-=epsilon
res[i]=(f(w_1,X)-f(w_2,X))/(2*epsilon)
return res
#对于每一次计算向量w之前都要进行单位化计算,使其模为1
def direction(w):
return w/np.linalg.norm(w)
def gradient_ascent(df,X,initial_w,eta,n_iters=1e4,epsilon=1e-8):
w=direction(initial_w)
cur_iter=0
while cur_iter<n_iters:
gradient=df(w,X)
last_w=w
w=w + eta * gradient
w=direction(w) #注意1:每次求一个单位方向
if abs(f(w,X)-f(last_w,X))<epsilon:
break
cur_iter+=1
return w
initial_w=np.random.random(X.shape[1]) #注意2:不能用0向量开始
eta=0.001
#注意3:不能使用Standardscaler标准化数据
gradient_ascent(df_debug,X_demean,initial_w,eta)
gradient_ascent(df_math,X_demean,initial_w,eta)
w=gradient_ascent(df_math,X_demean,initial_w,eta)
plt.scatter(X_demean[:,0],X_demean[:,1])
plt.plot([0,w[0]*30],[0,w[1]*30],color='r') #由于w较小,乘以一个系数便于观察
plt.show()
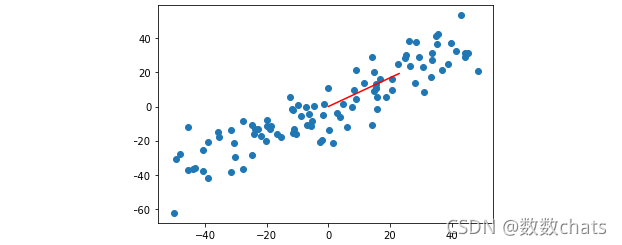
求出第一主成分以后,如何求出下一个主成分?
数据进行改变,将数据在第一个主成分上的分量去掉
在新的数据上求第一主成分
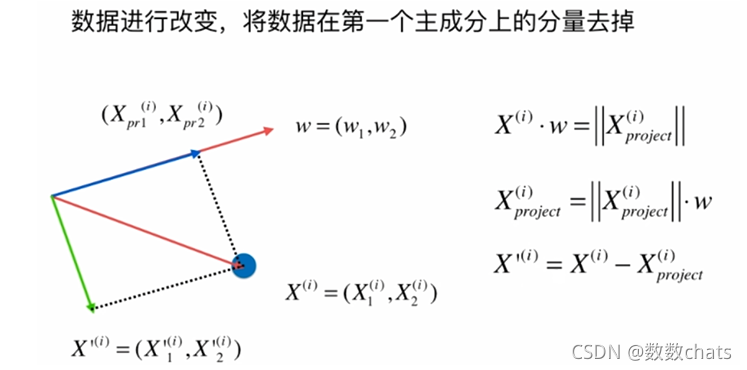
如上图所示,样本 X ( i ) X^{(i)} X(i) 在第一主成分w上的分量为 ( X p r 1 ( i ) , X p r 2 ( i ) ) (X_{pr1}^{(i)},X_{pr2}^{(i)}) (Xpr1(i),Xpr2(i)),也就是图中的蓝色向量,其模长是 X ( i ) X^{(i)} X(i) 向量和w向量的乘积,又因为w是单位向量,向量的模长乘以方向上的单位向量就可以得到这个向量。
求下一个主成分就是将数据在第一主成分上的分量去掉,再对新的数据求第一主成分。
那么如何去掉第一主成分呢?用样本 X ( i ) X^{(i)} X(i)减去分量 ( X p r 1 ( i ) , X p r 2 ( i ) ) (X_{pr1}^{(i)},X_{pr2}^{(i)}) (Xpr1(i),Xpr2(i)) (向量减法),得到结果的几何意义就是一条与第一主成分垂直的一个轴。这个轴就是样本数据去除第一主成分分量后得到的结果,即图中的绿色部分
这样就得到第二主成分,依此循环就可以得到第n主成分。
求第二主成分的步骤:
首先,我们要将数据集在第一个主成分上的分量去掉。即用样本 X ( i ) X^{(i)} X(i)减去样本在第一主成分分量上的映射,得到 X n e w X_new Xnew 。
阵(的矩阵)与向量(的矩阵)点乘,得到的是一个的向量,这个元素表示中的每一个样本映射到向量方向上的模长
然后对向量reshape,使其成真正的的矩阵
再乘以,得到的矩阵,也就是把矩阵中每个样本的每个维度在方向上的分量。即 x p r o j e c t x_{project} xproject
用样本减去样本在第一主成分上的映射
X_new = X - X.dot(w).reshape(-1,1) * w
plt.scatter(X_new[:,0], X_new[:,1])
plt.show()
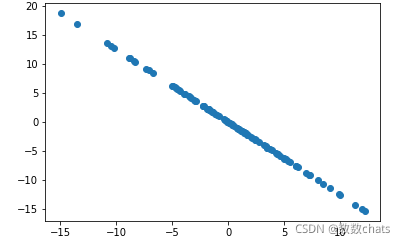
X2=np.empty(X.shape)
for i in range(len(X)):
X2[i]=X[i]-X[i].dot(w)*w
plt.scatter(X2[:,0],X2[:,1])
plt.show()
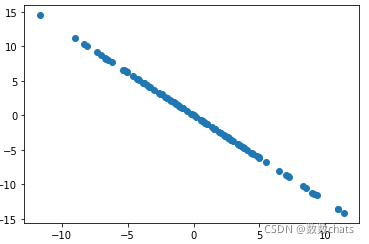
X2=np.empty((100,2))
X2[:,0]=np.random.uniform(0,100,size=100)
X2[:,1]=0.75*X2[:,0]+3
plt.scatter(X2[:,0],X2[:,1])
plt.show()
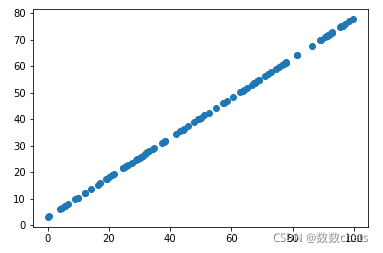
X2_demean=demean(X2)
w2=gradient_ascent(df_math,X2_demean,initial_w,eta)
plt.scatter(X2_demean[:,0],X2_demean[:,1])
plt.plot([0,w2[0]*30],[0,w2[1]*30],color='r')
plt.show()
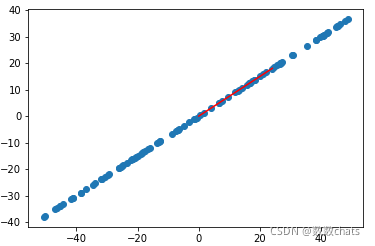
def f(w,X):
return np.sum((X.dot(w)**2))/len(X)
def df(w,X):
return X.T.dot(X.dot(w))*2/len(X)
def direction(w):
return w/np.linalg.norm(w)
def first_component(X,initial_w,eta,n_iters=1e4,epsilon=1e-8):
w=direction(initial_w)
cur_iter=0
while cur_iter<n_iters:
gradient=df(w,X)
last_w=w
w=w + eta * gradient
w=direction(w) #注意1:每次求一个单位方向
if abs(f(w,X)-f(last_w,X))<epsilon:
break
cur_iter+=1
return w
initial_w=np.random.random(X.shape[1]) #注意2:不能用0向量开始
eta=0.001
w=first_component(X,initial_w,eta)
w
w2=first_component(X2,initial_w,eta)
w2
w.dot(w2)
#求X的前n个主成分
def first_n_component(n,X,eta=0.01,n_iters=1e4,epsilon=1e-8):
X_pca=X.copy()
X_pca=demean(X_pca)
res=[]
#在for循环中每次求主成分时都设定一个随机的w(initial_w)
for i in range(n):
initial_w=np.random.random(X_pca.shape[1])
w=first_component(X_pca,initial_w,eta)
res.append(w)
#使用梯度上升法得到一个主成分后就去掉在这个主成分上的分量
X_pca=X_pca - X_pca.dot(w).reshape(-1,1)*w
return res
first_n_component(2,X)
高维数据向低维数据映射

import numpy as np
class PCA:
def __init__(self, n_components):
# 主成分的个数n
self.n_components = n_components
# 具体主成分
self.components_ = None
def fit(self, X, eta=0.001, n_iters=1e4):
'''均值归零'''
def demean(X):
return X - np.mean(X, axis=0)
'''方差函数'''
def f(w, X):
return np.sum(X.dot(w) ** 2) / len(X)
'''方差函数导数'''
def df(w, X):
return X.T.dot(X.dot(w)) * 2 / len(X)
'''将向量化简为单位向量'''
def direction(w):
return w / np.linalg.norm(w)
'''寻找第一主成分'''
def first_component(X, initial_w, eta, n_iters, epsilon=1e-8):
w = direction(initial_w)
cur_iter = 0
while cur_iter < n_iters:
gradient = df(w, X)
last_w = w
w = w + eta * gradient
w = direction(w)
if(abs(f(w, X) - f(last_w, X)) < epsilon):
break
cur_iter += 1
return w
# 过程如下:
# 归0操作
X_pca = demean(X)
# 初始化空矩阵,行为n个主成分,列为样本列数
self.components_ = np.empty(shape=(self.n_components, X.shape[1]))
# 循环执行每一个主成分
for i in range(self.n_components):
# 每一次初始化一个方向向量w
initial_w = np.random.random(X_pca.shape[1])
# 使用梯度上升法,得到此时的X_PCA所对应的第一主成分w
w = first_component(X_pca, initial_w, eta, n_iters)
# 存储起来
self.components_[i:] = w
# X_pca减去样本在w上的所有分量,形成一个新的X_pca,以便进行下一次循环
X_pca = X_pca - X_pca.dot(w).reshape(-1, 1) * w
return self
# 将X数据集映射到各个主成分分量中
def transform(self, X):
assert X.shape[1] == self.components_.shape[1]
return X.dot(self.components_.T)
def inverse_transform(self, X):
return X.dot(self.components_)
API
class sklearn.decomposition.PCA(n_components=None, *, copy=True, whiten=False, svd_solver='auto', tol=0.0, iterated_power='auto', random_state=None)
sklearn.decomposition.PCA(n_components=None)
- 将数据分解为较低维数空间
- n_components:
- 小数:表示保留百分之多少的信息
- 整数:指定降维到的维数
- copy:类型:bool,True或者False,缺省时默认为True。意义:表示是否在运行算法时,将原始训练数据复制一份。若为True,则运行PCA算法后,原始训练数据的值不会有任何改变,因为是在原始数据的副本上进行运算;若为False,则运行PCA算法后,原始训练数据的值会改,因为是在原始数据上进行降维计算。
- whiten :判断是否进行白化。所谓白化,就是对降维后的数据的每个特征进行归一化,让方差都为1.对于PCA降维本身来说,一般不需要白化。如果你PCA降维后有后续的数据处理动作,可以考虑白化。默认值是False,即不进行白化。
- .svd_solver:即指定奇异值分解SVD的方法,由于特征分解是奇异值分解SVD的一个特例,一般的PCA库都是基于SVD实现的。有4个可以选择的值:{‘auto’, ‘full’, ‘arpack’, ‘randomized’}。randomized一般适用于数据量大,数据维度多同时主成分数目比例又较低的PCA降维,它使用了一些加快SVD的随机算法。 full则是传统意义上的SVD,使用了scipy库对应的实现。arpack和randomized的适用场景类似,区别是randomized使用的是scikit-learn自己的SVD实现,而arpack直接使用了scipy库的sparse SVD实现。默认是auto,即PCA类会自己去在前面讲到的三种算法里面去权衡,选择一个合适的SVD算法来降维。一般来说,使用默认值就够了。
- tol:svd_solver =='arpack’计算的奇异值的公差,float> = 0,可选(默认.0)
- iterated_power: int> = 0或’auto’,(默认为’auto’),svd_solver =='随机化’计算出的幂方法的迭代次数。
属性
1.components_ :特征空间中的主轴,表示数据中最大方差的方向。组件按排序 explained_variance_
2.explained_variance_:它代表降维后的各主成分的方差值。方差值越大,则说明越是重要的主成分
3.explained_variance_ratio _ :它代表降维后的各主成分的方差值占总方差值的比例,这个比例越大,则越是重要的主成分,所有总和为1
4.singular_values:每个特征的奇异值,奇异值等于n_components 低维空间中变量的2范数
5.mean_:每个特征的均值
6.n_components_:即是上面输入的参数值
7.n_features_:训练数据中的特征数量
8.n_samples_:训练数据中的样本数
9.noise_variance_:等于X协方差矩阵的(min(n_features,n_samples)-n_components)个最小特征值的平均值
方法:
fit(X [,y])用X拟合模型。
fit_transform(X [,y]) 使用X拟合模型,并在X上应用降维。
get_covariance() 用生成模型计算数据协方差。
get_params() 获取此估计量的参数。
get_precision() 用生成模型计算数据精度矩阵。
inverse_transform(X)将数据转换回其原始空间。
score(X [,y]) 返回所有样本的平均对数似然率。
score_samples(X) 返回每个样本的对数似然。
set_params(**参数) 设置此估算器的参数。
transform(X) 对X应用降维。
from sklearn.decomposition import PCA
def pca_demo():
"""
对数据进行PCA降维
:return: None
"""
data = [[2,8,4,5], [6,3,0,8], [5,4,9,1]]
# 1、实例化PCA, 小数——保留多少信息
transfer = PCA(n_components=0.9)
# 2、调用fit_transform
data1 = transfer.fit_transform(data)
print("保留90%的信息,降维结果为:\n", data1)
# 1、实例化PCA, 整数——指定降维到的维数
transfer2 = PCA(n_components=3)
# 2、调用fit_transform
data2 = transfer2.fit_transform(data)
print("降维到3维的结果:\n", data2)
return None
if __name__ == '__main__':
pca_demo()
from sklearn.decomposition import PCA
def pca_demo():
data = [[2,8,4,5], [6,3,0,8], [5,4,9,1]]
transfer = PCA(n_components=0.9)
transfer.fit(data)
data = transfer.transform(data)
print("返回模型的各个特征向量",transfer.components_) #返回模型的各个特征向量(原始数据)
print("返回各个成分各自的方差",transfer.explained_variance_ )
print("返回各个成分各自的方差百分比(贡献率)",transfer.explained_variance_ratio_ )
print("保留90%的信息,降维结果为:\n", data)
inv_d=transfer.inverse_transform(data) #将降维后的数据转换成原始数据
print("inverse:\n",inv_d)
return None
if __name__ == '__main__':
pca_demo()
降维算法pca的应用
PCA的作用大致有三个:降低维度(将X从高纬度映射到低维度)、加快运算(维度约简后运算量降低)。
降维加快运算案例
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
digits = datasets.load_digits()
X = digits.data
y = digits.target
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train, y_train)
knn_clf.score(X_test, y_test)
#0.9866666666666667
#下面用PCA算法对数据进行降维:
from sklearn.decomposition import PCA
pca = PCA(n_components=2) # 预先设置主成分有2个
pca.fit(X_train)
X_train_reduction = pca.transform(X_train) # 训练数据集降维结果 。X都需要降维,y不需要
X_test_reduction = pca.transform(X_test) # 测试数据集降维结果
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train_reduction, y_train)
knn_clf.score(X_test_reduction, y_test)
#0.6066666666666667
print(pca.explained_variance_ratio_)
# pca.explained_variance_ratio_(解释方差比例),我们可以使用这个指标找到某个数据集保持多少的精度:[0.14566817 0.13735469]
显然主成分个数是个超参数,那么如何设置主成分个数n_components了?
对于pca = PCA(n_components=2) 来说,0.14566817表示第一个轴能够解释14.56%数据的方差;0.13735469表示第二个轴能够解释13.73%数据的方差。对于这两个维度来说,[ 0.14566817, 0.13735469]涵盖了原数据的总方差的28%左右的信息,剩下72%的方差信息就丢失了,显然丢失的信息过多。
实际sklearn使用pca = PCA(0.95) 就可以保证传入95%以上的信息。
pca = PCA(0.95)
pca.fit(X_train)
# 输出:
PCA(copy=True, iterated_power='auto', n_components=0.95, random_state=None,
svd_solver='auto', tol=0.0, whiten=False)
# 查看主成分个数
pca.n_components_
#28
然后用这种pca去重新使用kNN做训练,得到的结果较好。
X_train_reduction = pca.transform(X_train)
X_test_reduction = pca.transform(X_test)
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train_reduction, y_train)
knn_clf.score(X_test_reduction, y_test)
# 0.98
降维的好处缩减了计算时间
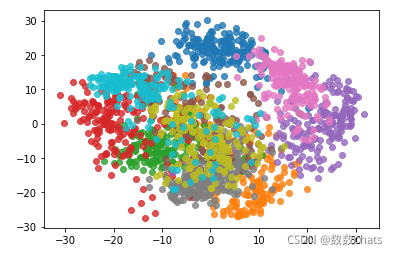
数据降维还有一个作用是可视化,降到2维数据之后:
#数据降维还有一个作用是可视化,降到2维数据之后:
pca = PCA(n_components=2)
pca.fi
t(X)
X_reduction = pca.transform(X)
for i in range(10):
plt.scatter(X_reduction[y==i,0], X_reduction[y==i,1], alpha=0.8)
plt.show()
去噪案例
PCA通过选取主成分将原有数据映射到低维数据再映射回高维数据的方式进行一定程度的降噪。
import numpy as np
import matplotlib.pyplot as plt
X = np.empty((100, 2))
X[:,0] = np.random.uniform(0., 100., size=100)
X[:,1] = 0.75 * X[:,0] + 3. + np.random.normal(0, 5, size=100) # 线性方程加一个正态分布的随机扰动项
plt.scatter(X[:,0], X[:,1])
plt.show()
# np.random.normal(0, 5, size=100) 是我们添加的噪音:随机数的均值、方差以及输出的size(可数可(2,2))
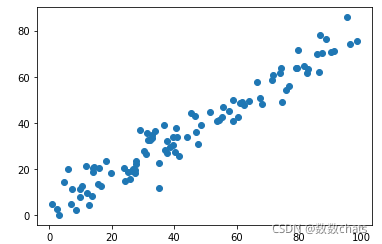
我们降噪,这就需要使用PCA中的一个方法:X_ori=pca.inverse_transform(X_pca),将降维后的数据转换成与维度相同数据。要注意,还原后的数据,不等同于原数据!
这是因为在使用PCA降维时,已经丢失了部分的信息(忽略了解释方差比例)。因此在还原时,只能保证维度相同。会尽最大可能返回原始空间,但不会跟原来的数据一样。
from sklearn.decomposition import PCA
pca = PCA(n_components=1)
pca.fit(X)
X_reduction = pca.transform(X)
X_restore = pca.inverse_transform(X_reduction)
plt.scatter(X_restore[:,0], X_restore[:,1])
plt.show()
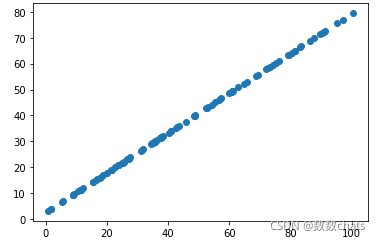
transform降维成一维数据,再inverse_transform返回成二维数据。此时数据成为了一条直线。这个过程可以理解为将原有的噪音去除了。
当然,我们丢失的信息也不全都是噪音。我们可以将PCA的过程定义为:降低了维度,丢失了信息,也去除了一部分噪音。
去除噪音,不仅仅去除的是数字噪音,图片中的噪音也可以通过PCA方法进行去噪
手写数字去噪
from sklearn import datasets
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
digits = datasets.load_digits()
X = digits.data
y = digits.target
# 添加一个正态分布的噪音矩阵
noisy_digits = X + np.random.normal(0, 4, size=X.shape)
# 绘制噪音数据:从y==0数字中取10个,进行10次循环;
# 依次从y==num再取出10个,将其与原来的样本拼在一起
example_digits = noisy_digits[y==0,:][:10]
for num in range(1,10):
example_digits = np.vstack([example_digits, noisy_digits[y==num,:][:10]])
example_digits.shape
# 输出:
# (100, 64) # 即含有100个数字(0~9各10个),每个数字有64维
# 手写数字 ,用的是包里面的数据;工程中如何构建满足pca模型的原始图库,这个很耗费时间?!
def plot_digits(data):
fig, axes = plt.subplots(10, 10, figsize=(10, 10),
subplot_kw={
'xticks':[], 'yticks':[]},
gridspec_kw=dict(hspace=0.1, wspace=0.1))
for i, ax in enumerate(axes.flat):
ax.imshow(data[i].reshape(8, 8),
cmap='binary', interpolation='nearest',
clim=(0, 16))
plt.show()
plot_digits(example_digits)
# 采用pca 处理后的去除噪音
pca = PCA(0.5).fit(noisy_digits)
pca.n_components_
# 输出:12,即原始数据保存了50%的信息,需要12维
# 进行降维、还原过程
components = pca.transform(example_digits)
filtered_digits = pca.inverse_transform(components)
plot_digits(filtered_digits)