在机器学习中,对高维数据进行降维的主要目的是希望找到一个合适的低维空间,在此空间中进行学习能比原始空间性能更好。
主成分分析(Principai Component Analysis,简称PCA)是最常用的一种降维方法。在介绍PCA之前,不妨先考虑这样一个问题:对于正交属性空间中的样本点,如何用一个超平面(直线的高维推广)对所有样本进行恰当的表达?
容易想到,若存在这样的超平面,那么它大概具有这样的性质:
·最近重构性:样本点到这个超平面的距离都足够近
·最大可分性:样本点在这个超平面上的投影能尽可能分开
有趣的是,基于最近重构性和最大可分性,能分别得到主成分分析的两种等价推导。
1> 最近重构性推导:
假定数据样本进行了中心化,即Σxi = 0;再假设投影变换后得到的新坐标系为{w1,w2,...,wd},其中wi是标准正交基向量,||wi||² = 1,wi(T)*wj = 0(i ≠ j)。若丢弃新坐标系中的部分坐标,即将维度降低到d' < d,则样本点xi在低维坐标系中的投影是zi =(zi1;zi2;...;zid'),其中zij=wj(T)*xi在低维坐标系下第j维的坐标。若基于zi来重构xi,则会得到xi' = Σzijwj。
考虑整个训练集,原样本点xi与基于投影重构的样本点xi'之间的距离为:
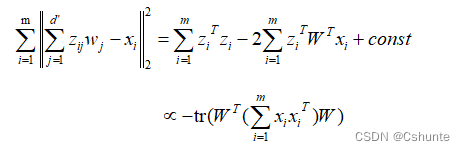
其中W = (w1,w2,...,wd)。根据最近重构性,上式应被最小化,考虑到wj是标准正交基,Σxixi(T)是协方差矩阵,有:

这就是主成分分析的优化目标。
2> 最大可分性推导:
从最大可分性出发,能得到主成分分析的另一种解释。我们知道样本点xi在新空间中超平面上的投影式W(T)xi,若所有样本点的投影能尽可能分开,则应该使投影后样本点的方差最大。如下图所示:(画得有点拉...可意会不可图传)
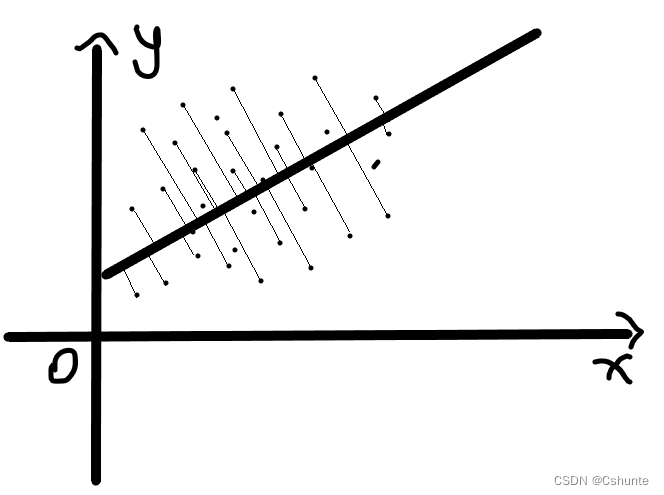
投影后样本点的协方差矩阵是ΣW(T)xixi(T)W,于是优化目标可写为:

显然,由最近重构性和最大可分性推导而来的两条式子是等价的。
对上式使用拉格朗日乘子法可得:
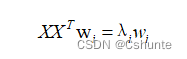
于是只需对协方差矩阵XX(T)进行特征值分解,将求得的特征值排序:λ1≥λ2≥...≥λd,再取前d'个特征值对应的特征向量构成W*=(w1,w2,...,wd')。这就是主成分分析的解。PCA算法描述如下所示:
输入:样本集D = {x1,x2,...,};
低维空间维数d'
过程:
1.对所有样本进行中心化:xi <- xi-(Σxi)/m
2.计算样本的协方差矩阵XX(T)
3.对协方差矩阵XX(T)做特征值分解
4.取最大的d'个特征值所对应的特征向量w1,w2,...,wd'
输出:投影矩阵W* = (w1,w2,...,wd')降维后低维空间的维数d’通常是由用户事先指定,或通过在d'值不同的低维空间中对k近邻分类器(或其他开销较小的学习器)进行交叉验证来选取较好的d'值。对PCA,还可以从重构的角度设置一个重构阈值,例如t = 95%,然后选取使下式成立的最小d'值:
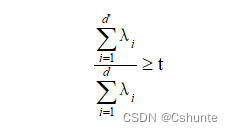
PCA仅需保留W*与样本的均值向量即可通过简单的向量减法和矩阵-向量乘法将新样本投影至低维空间中。显然,低维空间与原始高维空间必有不同,因为对应于最小的d-d'个特征值的特征向量被舍弃了,这是降维导致的结果。但舍弃这部分信息往往是必要的:一方面,舍弃这部分信息之后能使样本的采样密度增大,这正是将为的重要动机;另一方面,当数据收到噪声影响时,最小的特征值所对应的特征向量往往与噪声有关,将它们舍弃能在一定程度上起到去噪的效果。
参考周志华《机器学习》