目录
一、分段三次样条插值曲线推导
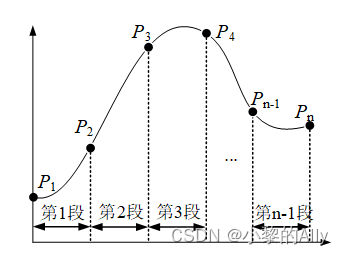
如图 1所示,设有n个离散点 ,我们希望用一条光滑的曲线依次经过这n个离散点。上文讲到,若用一条高阶多项式曲线进行插值,会出现端点振荡的龙格现象。
因此我们设想用若干段低阶的多项式曲线分别插值相邻两个点,然后将其首位相连构成一条光滑的完整曲线。回到图1,n个离散点对应n-1个区间段,也就是说我们的目标转化为求解n-1段三次曲线,每段三次曲线的表达式如下:
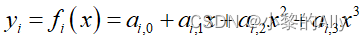
上式中, fi(x)代表第i段三次曲线函数, ai,j 代表第i段三次曲线的j次项系数。
由式1可知,每段三次曲线有4个待定系数,那么n-1段三次曲线总共有4(n-1)个待定系数,故需要构造4(n-1)个独立方程才能获得唯一解。换言之,我们需要设定4(n-1)个独立的边界条件,构造边界条件的过程其实也是探索多段三次曲线的等式约束过程,可以从如下几个方面考虑。
1. 邻接点的函数值相等
显然,我们希望每一段的三次曲线的首末两个点函数值等于离散点,表达式如下:
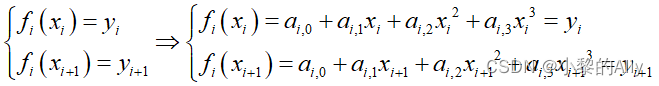
改用矩阵表达:
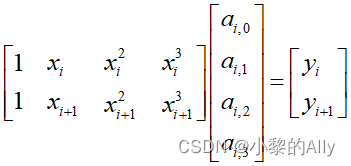
式中,xi和yi分别代表离散点 的横坐标和纵坐标。因此,根据邻接点的函数值相等这一等式约束可以构造2(n-1)个边界条件。
2. 邻接点的一阶导相等
为了保证曲线在邻接点的导数连续,需要保证邻接点的一阶导相等:
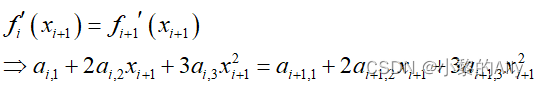
改用矩阵表达:
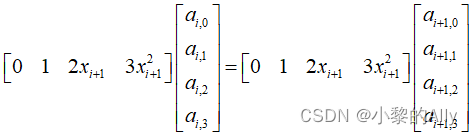
因此,根据邻接点的一阶导相等这一等式约束可以构造(n-2)个边界条件。
3. 邻接点的二阶导相等
为了保证曲率连续,邻接点的二阶导也需要相等:
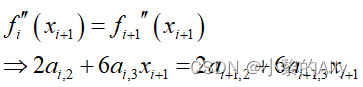
改用矩阵表达:
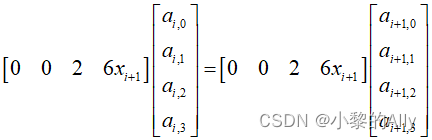
根据邻接点的二阶导相等这一等式约束可以构造(n-2)个边界条件。
4. 端点边界条件
端点边界条件分为自然边界、固定边界、扭结边界。针对自然边界,指定端点的二阶导数为0,即
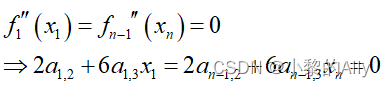
改用矩阵表达:
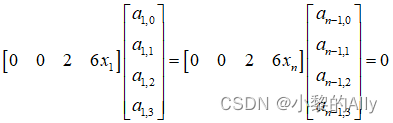
根据端点条件这一等式约束可以构造2个边界条件。
综上,我们可以将上述的4(n-1)个等式约束全部用矩阵表达式统一表达,最后构成一个线型矩阵方程,因此可以用MATLAB进行矩阵计算求解得到4(n-1)个待定系数。
二、案例精讲与MATLAB仿真
1. 场景介绍
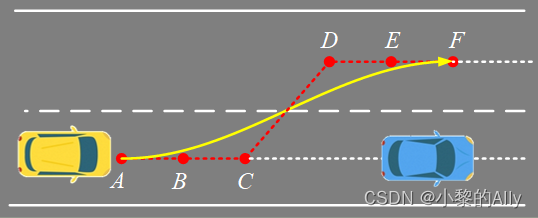
图2是一个典型的局部路径规划示意图, 蓝车作为障碍车,黄车需要换道避障。我们设A(0,-1.75),B(10,-1.75) , C(20,-1.75) , D(30,1.75) , E(40,1.75) , F(50,1.75) 一共6个离散点,可以利用三次样条曲线进行路径规划。
MATLAB的分段三次 Hermite 插值多项式库函数pchip,该函数可以直接计算分段三次样条,返回每一段多项式的4个系数,然后根据此系数调用ppval库函数,生成一系列的插值点,从而得到三次样条曲线。
2. MATLAB程序
主程序如下:
% 基于三次样条曲线的换道路径规划
clc
clear
close all
%% 数据定义
d = 3.5;
k = 4;
P = [0,-d/2; 10,-d/2; 20,-d/2; 30,d/2; 40,d/2; 50,d/2]';
%% 调用pchip函数,生成三次样条曲线
x_seq = P(1,:);
y_seq = P(2,:);
cs = pchip(x_seq,y_seq);
X_seq = linspace(0,50,100);
Y_seq = ppval(cs,X_seq);
path = [X_seq', Y_seq'];
%% 计算长度和曲率
x = path(:,1)';
y = path(:,2)';
diffX = diff(path(:,1));
diffY = diff(path(:,2));
cumLength = cumsum(sqrt(diffX.^2 + diffY.^2)); %长度
heading = atan2(diffY, diffX);
for i = 1:length(x)-2
cur(i) = getCur(x(i:i+2)',y(i:i+2)');
end
cur(end+1) = cur(end);
%% 画曲率图
figure
hold on
grid on
% 主体图形绘制
plot(cumLength,cur,'LineWidth', 3, 'Color', 'k');
% 坐标轴
set(gca,'LineWidth',2.5,'FontName', 'Times New Roman')
hXLabel = xlabel('路径长度/m');
hYLabel = ylabel('曲率/m^-^1');
% 修改刻度标签字体和字号
set(gca, 'FontSize', 16),...
set([hXLabel, hYLabel], 'FontName', 'simsun')
set([hXLabel, hYLabel], 'FontSize', 16)
% 画航向角图
figure
hold on
grid on
% 主体图形绘制
plot(cumLength, heading,'LineWidth', 3, 'Color', 'b');
% 坐标轴
set(gca,'LineWidth',2.5,'FontName', 'Times New Roman')
hXLabel = xlabel('路径长度/m');
hYLabel = ylabel('航向角/rad');
% 修改刻度标签字体和字号
set(gca, 'FontSize', 16),...
set([hXLabel, hYLabel], 'FontName', 'simsun')
set([hXLabel, hYLabel], 'FontSize', 16)
%% 画图
d = 3.5; % 道路标准宽度
W = 1.8; % 汽车宽度
L = 4.7; % 车长
figure
len_line = 50;
% 画灰色路面图
GreyZone = [-5,-d-0.5; -5,d+0.5; len_line,d+0.5; len_line,-d-0.5];
fill(GreyZone(:,1),GreyZone(:,2),[0.5 0.5 0.5]);
hold on
fill([P(1,1),P(1,1),P(1,1)-L,P(1,1)-L],[-d/2-W/2,-d/2+W/2,-d/2+W/2,-d/2-W/2],'y')
fill([35,35,35-L,35-L],[-d/2-W/2,-d/2+W/2,-d/2+W/2,-d/2-W/2],'b')
% 画分界线
plot([-5, len_line],[0, 0], 'w--', 'linewidth',2); %分界线
plot([-5,len_line],[d,d],'w','linewidth',2); %左边界线
plot([-5,len_line],[-d,-d],'w','linewidth',2); %左边界线
% 设置坐标轴显示范围
axis equal
set(gca, 'XLim',[-5 len_line]);
set(gca, 'YLim',[-4 4]);
% 绘制路径
scatter(P(1,:),P(2,:),100,'r.')
plot(P(1,:),P(2,:),'r');%路径点
plot(path(:,1),path(:,2), 'y','linewidth',2);%路径点
上面的主程序使用了求解散点曲率的函数,函数体程序如下
function k=getCur(x,y)
ta=sqrt((x(2)-x(1))^2+(y(2)-y(1))^2);
tb=sqrt((x(3)-x(2))^2+(y(3)-y(2))^2);
M=[1,-ta,ta^2;
1,0,0;
1,tb,tb^2];
A=M\x;
B=M\y;
k=(2*(A(2)*B(3)-A(3)*B(2)))/((A(2)^2+B(2)^2)^1.5+1e-10);
end3. 仿真结果
执行上述代码,将场景图和规划路径一并绘制,如图3所示。

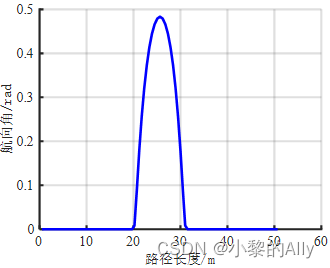
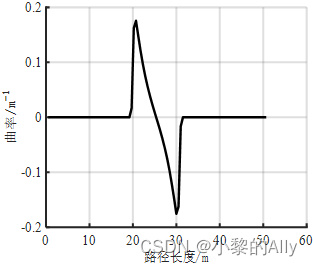
可以看出,三次样条曲线的曲率变化率较大,这与控制点的选取有较大关系。