系列文章目录
提示:这里可以添加系列文章的所有文章的目录,目录需要自己手动添加
TODO:写完再整理
前言
认知有限,望大家多多包涵,有什么问题也希望能够与大家多交流,共同成长!
通常平滑的运动轨迹都用5次多项式拟合,【防盗标记–盒子君hzj】应为它的加速度轨迹使一条抛物线,在提供了起始时间和终点时间后,满足低阶平滑连续性,就可以推导出来,常用的曲线拟合方法有:三次多项式插值拟合、五次多项式插值拟合、高阶多项式(一般超过5次会发散)
本文先对基于三次样条插值的路径生成方法做个简单的介绍,具体内容后续再更,其他模块可以参考去我其他文章
提示:以下是本篇文章正文内容
一、直线插值、二次样条插值、三次样条插值生成路径效果对比

.
.
1.直线插值(y = ax + b)效果

.
.
2.二次样条插值(y = ax² + bx + c)效果

.
.
3.三次样条插值(y = ax³ + bx² + c)效果

.
.
4.三次样条的一些性质
1、三次样条曲线在衔接点处是连续光滑的
2、三次样条的一阶导数和二阶导数是连续的
3、自由边界三次样条(Nature Cubic Spline)的边界二阶导数也是连续的
4、单个点并不会影响到整个插值曲线
.
.
二、三次样条插值的路径生成实现
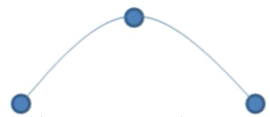
假定有三个点需要拟合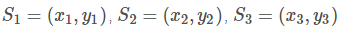
.
1.人为数学推导过程(代数的方法–方程组不断的代入求解)
假定有三个点需要拟合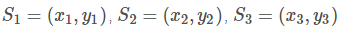
那么我们可以使用一个三次函数来拟合 (S1,S2) 两个点, 用另一个三次函数来拟合 (S2,S3) 两个点,这两个三次函数分别记做:
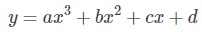
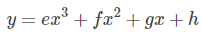
由这两个三次样条函数曲线,代入对应的点S1、S3可得如下两个方程:
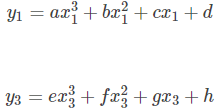
由两条三次样条函数曲线都经过点 S2 , 故可得
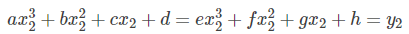
由于样条曲线在衔接点处的导数也连续,即两个三次函数在 S2 处的一阶导数也相等,可得:

如果是自由边界三次样条,那么要求在起点和终点的二阶导数也是连续的,即:
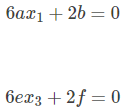
结合以上6个方程组以及给定的点集,通过代数计算来确定两段3次样条的多项式系数(a,b,c,d,e,f,g,h)
在实际样条参数求解过程中,在确定一段样条的多项式系数(即a,b,c,d)以后,即得到了对应的路径(可以用样条曲线表达式求出路径,即完成了路径生成)
.
.
2.计算机推导的过程(计算机算法–数值分析)
次样条插值的计算机算法,考虑到该算法的推导过程涉及到数值分析等基础,且和无人驾驶的主题相去甚远,故不讨论该算法的推导,感兴趣的同学可以自行扩展阅读。
假定目前有n+1个路径点,它们分别是:(x0,y0),(x1,y1),(x2,y2),…,(xn,yn)(x0,y0),(x1,y1),(x2,y2),…,(xn,yn),求解每一段样条曲线的系数:(ai,bi,ci,di)(ai,bi,ci,di),有如下算法:
1、计算点与点之间的步长
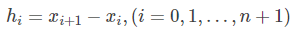
2、将路径点和端点条件(如果是自由边界三次样条中端点条件即S′′=0)代入如下矩阵方程中

3、解矩阵方程,求得二次微分值mi
.
4、计算每一段的三次样条曲线系数

5、那么在每一个子区间 xi≤x≤xi+1 内,其对应的样条函函数表达式为
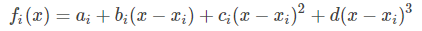
至此,我们就得到了每相邻两点的三次样函数条表达式,每段三次样条曲线连接起来就是全局路径
.
.
三、使用Python实现自由边界三次样条插值进行路径生成
# coding=utf-8
import numpy as np
import bisect
class Spline:
"""
三次样条类
"""
def __init__(self, x, y):
self.a, self.b, self.c, self.d = [], [], [], []
self.x = x
self.y = y
self.nx = len(x) # dimension of x
h = np.diff(x)
# calc coefficient c
self.a = [iy for iy in y]
# calc coefficient c
A = self.__calc_A(h)
B = self.__calc_B(h)
self.m = np.linalg.solve(A, B)
self.c = self.m / 2.0
# calc spline coefficient b and d
for i in range(self.nx - 1):
self.d.append((self.c[i + 1] - self.c[i]) / (3.0 * h[i]))
tb = (self.a[i + 1] - self.a[i]) / h[i] - h[i] * (self.c[i + 1] + 2.0 * self.c[i]) / 3.0
self.b.append(tb)
def calc(self, t):
"""
计算位置
当t超过边界,返回None
"""
if t < self.x[0]:
return None
elif t > self.x[-1]:
return None
i = self.__search_index(t)
dx = t - self.x[i]
result = self.a[i] + self.b[i] * dx + \
self.c[i] * dx ** 2.0 + self.d[i] * dx ** 3.0
return result
def __search_index(self, x):
return bisect.bisect(self.x, x) - 1
def __calc_A(self, h):
"""
计算算法第二步中的等号左侧的矩阵表达式A
"""
A = np.zeros((self.nx, self.nx))
A[0, 0] = 1.0
for i in range(self.nx - 1):
if i != (self.nx - 2):
A[i + 1, i + 1] = 2.0 * (h[i] + h[i + 1])
A[i + 1, i] = h[i]
A[i, i + 1] = h[i]
A[0, 1] = 0.0
A[self.nx - 1, self.nx - 2] = 0.0
A[self.nx - 1, self.nx - 1] = 1.0
return A
def __calc_B(self, h):
"""
计算算法第二步中的等号右侧的矩阵表达式B
"""
B = np.zeros(self.nx)
for i in range(self.nx - 2):
B[i + 1] = 6.0 * (self.a[i + 2] - self.a[i + 1]) / h[i + 1] - 6.0 * (self.a[i + 1] - self.a[i]) / h[i]
return B
其中方法 __calc_A 和 __calc_B 分别用于构建上述算法第二步中的方程左右矩阵,由于 m 为对对角矩阵,这里我们直接使用Numpy中的linalg.solve 求解 m 。下面我们新建一个 test.py 文件来执行测试代码:
import cubic_spline
import numpy as np
import matplotlib.pyplot as plt
def main():
x = [-4., -2, 0.0, 2, 4, 6, 10]
y = [1.2, 0.6, 0.0, 1.5, 3.8, 5.0, 3.0]
spline = cubic_spline.Spline(x, y)
rx = np.arange(-4.0, 10, 0.01)
ry = [spline.calc(i) for i in rx]
plt.plot(x, y, "og")
plt.plot(rx, ry, "-r")
plt.grid(True)
plt.axis("equal")
plt.show()
if __name__ == '__main__':
main()
生成路径的结果:

总结
1、每段三次样条曲线连接起来就是全局路径
2、把样条理解成曲线就行
3、三次样条曲线插值的思想可以迁移到理解五次多项式样条曲线的求解上,下一章我讲讲五次样条拟合与mini_snap吧,一脉相承
4、在实际中,需要使用C++来完成这些工作,我们通常不需要自己实现样条插值,有很多成熟的Spline开源代码,我们可以使用:http://kluge.in-chemnitz.de/opensource/spline/ 提供的代码迅速的实现C++的三次样条插值
参考资料
三次样条曲线路径生成
https://www.bilibili.com/video/BV1b64y1h79j?spm_id_from=333.999.0.0
三次样条曲线生成+pure_pursuit跟踪
https://www.bilibili.com/video/BV1RP4y1s7VS?spm_id_from=333.999.0.0