文章目录
前言
在机器学习中,优化模型参数是非常关键的一步。针对不同的模型和数据集,我们需要选择合适的优化方法以获得最优的模型参数。同时,正则化方法可以有效减少模型复杂程度,避免过拟合的情况,提高模型的泛化能力。
一、简单线性回归方程实现
我们可以通过python代码去实现这个过程
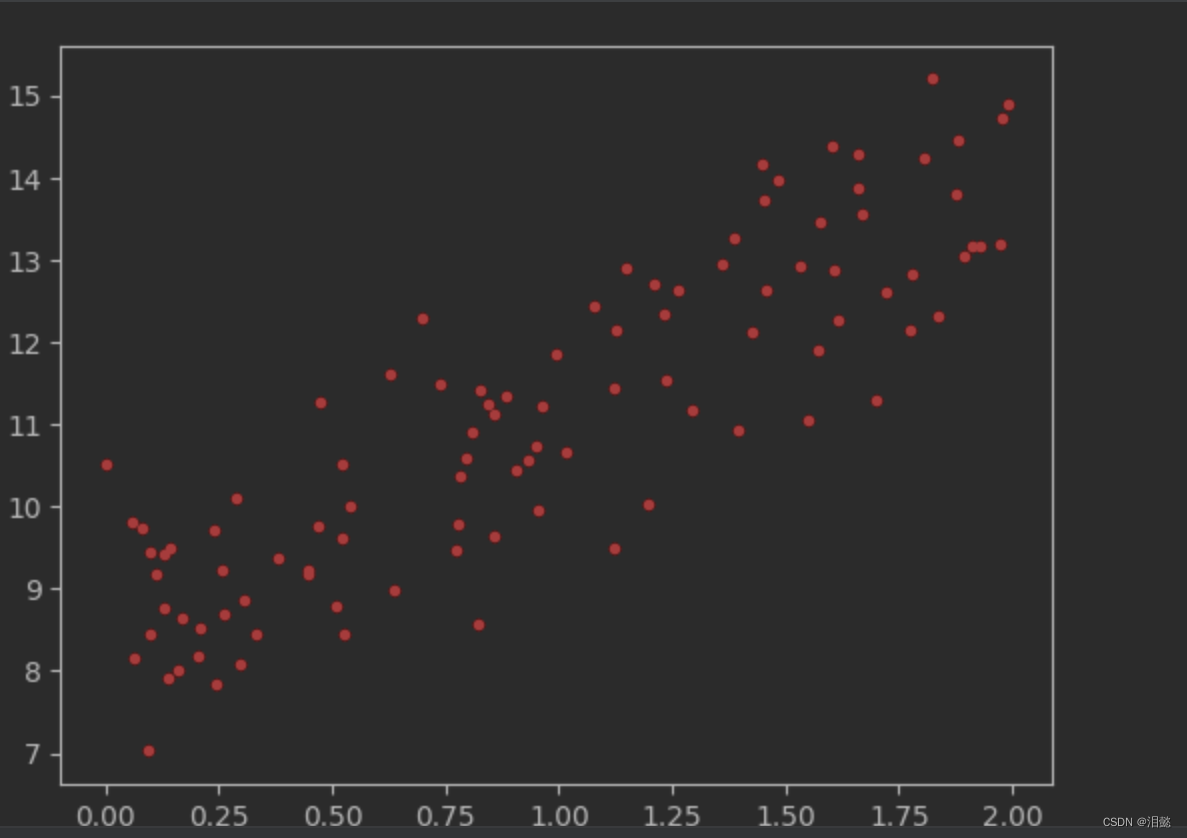
- 构建数据集(y=8+2*x+p)
X=2*np.random.rand(100,1)#生成shape为(100,1)的随机矩阵,矩阵的值为0,到2
y=8+3*X+np.random.randn(100,1)#
我们先绘制图像观察聚数据情况
plt.plot(X,y,'r.')
plt.show()
产生偏置项
X_b = np.c_[np.ones((100,1)),X]
X_b = np.c_[np.ones((100,1)), X] 的作用是给数据集 X 添加一列常数项,即偏置项(bias term),生成新的数据集 X_b,其中 np.ones((100,1)) 用于创建一个100行1列的全1数组。
在机器学习中,线性回归模型通常表示为 y = Xw + b,其中 y 表示目标变量(target variable),X 表示自变量(independent variable),w 表示权重(weights),b 表示偏置(bias)。在给定自变量 X 的情况下,线性回归模型的目标是找到最佳权重和偏置,使得预测结果最接近真实结果。
在实际应用中,通常需要将自变量 X 增加一列常数项 b,即将 X 扩展为 [X, 1],这是因为常数项可以被视为自变量的一种特殊取值,当自变量全部为0时,常数项等于1,这有助于模型更好地拟合数据集。
因此,通过添加常数项,我们可以更准确地预测目标变量 y,而 X_b = np.c_[np.ones((100,1)),X] 就是用于实现这一目的的代码。
回归方程代码实现
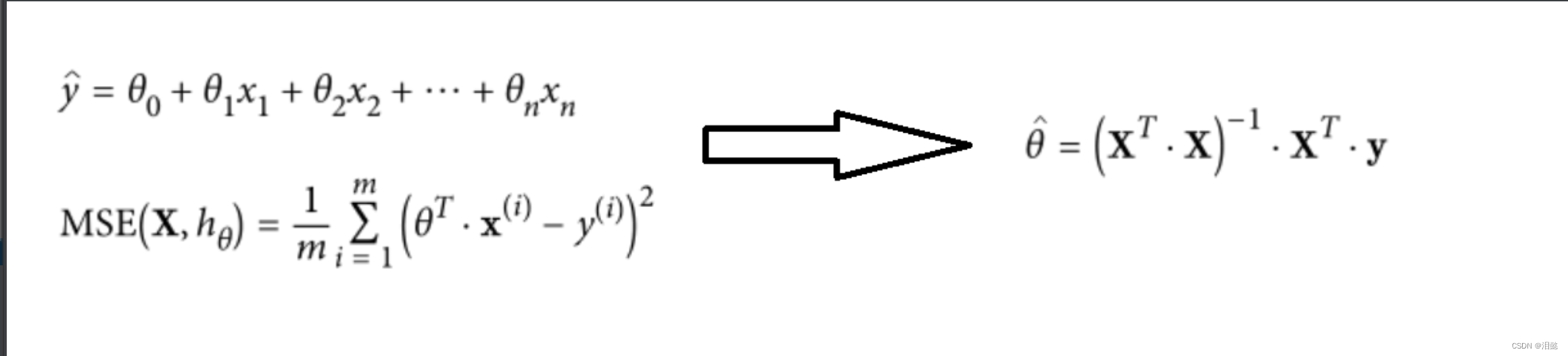
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
我们打印一下看看
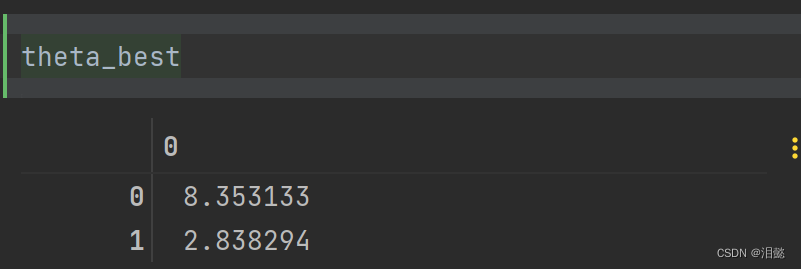
得到损失函数,第一个数字是权重,第二个偏置项,用来调整模型的参数
- 生成测试数据,预测,观察
X_new = np.array([[0],[2]])
X_new_b = np.c_[np.ones((2,1)),X_new]
y_predict = X_new_b.dot(theta_best)
y_predict
plt.plot(X_new,y_predict,'b--')
plt.plot(X,y,'r.')
plt.axis([0,2,6,15])
plt.show()
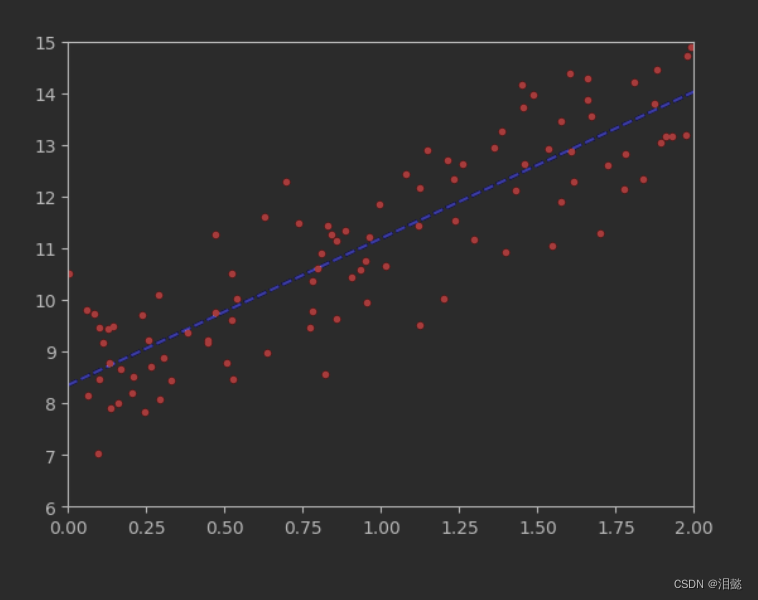
可以看到预测的数据还是基本拟合这个过程
二、梯度下降三种方式实现以及对比
1.批量梯度下降
- 公式

python 代码实现
eta=0.1
interations=1000
m=100
theta=np.random.rand(2,1)
for iteration in range(interations):
gradients = 2/m* X_b.T.dot(X_b.dot(theta)-y)
theta = theta - eta*gradients
我们查看不同的学习率对拟合过程的影响
theta_path_bgd = []
def plot_gradient_descent(theta,eta,theta_path = None):
m = len(X_b)
plt.plot(X,y,'r.')
n_iterations = 1000
for iteration in range(n_iterations):
y_predict = X_new_b.dot(theta)
plt.plot(X_new,y_predict,'b-')
gradients = 2/m* X_b.T.dot(X_b.dot(theta)-y)
theta = theta - eta*gradients
if theta_path:
theta_path.append(theta)
plt.xlabel('X_1')
plt.axis([0,2,0,15])
plt.title('eta = {}'.format(eta))
theta = np.random.randn(2,1)
plt.figure(figsize=(10,4))
plt.subplot(131)
plot_gradient_descent(theta,eta = 0.01)
plt.subplot(132)
plot_gradient_descent(theta,eta = 0.1,theta_path=theta_path_bgd)
plt.subplot(133)
plot_gradient_descent(theta,eta = 0.4)
plt.show()

可以观察到学习率越小,梯度更新次数越多,越耗费时间,我们需要保证准确性的前提下使学习率越大越好。显然这3个中学习率为0.1的时候最好
2.随机梯度下降
theta_path_sgd=[]
m = len(X_b)
np.random.seed(42)
n_epochs = 100
t0 = 5
t1 = 50
def learning_schedule(t):
return t0/(t1+t)
theta = np.random.randn(2,1)
for epoch in range(n_epochs):
for i in range(m):
if epoch < 10 and i<10:
y_predict = X_new_b.dot(theta)
plt.plot(X_new,y_predict,'b-')
random_index = np.random.randint(m)
xi = X_b[random_index:random_index+1]
yi = y[random_index:random_index+1]
gradients = 2* xi.T.dot(xi.dot(theta)-yi)
eta = learning_schedule(epoch*m+i)
theta = theta-eta*gradients
theta_path_sgd.append(theta)
plt.plot(X,y,'r.')
plt.axis([0,2,0,15])
plt.show()
这段代码实现了随机梯度下降算法(Stochastic Gradient Descent,SGD)来拟合一个简单的线性回归模型。代码参数的解释:
theta_path_sgd=[]:初始化theta_path_sgd为空列表,用于存储每个迭代步骤的模型参数。
m = len(X_b):数据集大小。
np.random.seed(42):设置随机种子,保证每次运行代码时得到的随机数相同。
n_epochs = 100:设置训练迭代的次数。
t0 = 5 和 t1 = 50:设置学习率调度函数中的超参数。
def learning_schedule(t)::定义学习率调度函数,根据给定的t值返回相应的学习率。
theta = np.random.randn(2,1):初始化模型参数θ为一个2行1列的随机向量。
for epoch in range(n_epochs)::开始进行n_epochs次训练迭代。
for i in range(m)::遍历整个数据集进行梯度下降更新模型参数。
if epoch < 10 and i<10::可视化代码,用于在前10个步骤中绘制模型的拟合直线。
random_index = np.random.randint(m):随机选择一个样本的索引。
xi = X_b[random_index:random_index+1] 和 yi = y[random_index:random_index+1]:根据选择的索引从数据集中选择一个随机样本进行训练。
gradients = 2* xi.T.dot(xi.dot(theta)-yi):计算随机样本的梯度。
eta = learning_schedule(epoch*m+i):计算当前迭代步骤的学习率。
theta = theta-eta*gradients:使用梯度下降法更新模型参数。
theta_path_sgd.append(theta):将更新后的模型参数θ添加到theta_path_sgd列表中。
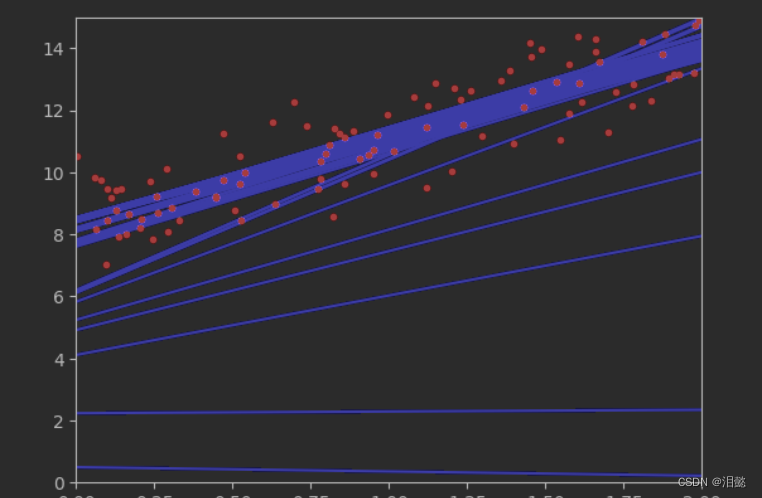
我们从图中可以发现,梯度刚开始的时候变化幅度比较大,后面越来越小,越接近拟合约小,换句话说刚开始做工艺品制作刚开始时候很快,后面要慢慢的要好的时候要小心一点,慢慢的来
3.小批量梯度下降
theta_path_mgd=[]
n_epochs = 100
minibatch = 16
theta = np.random.randn(2,1)
t0, t1 = 200, 1000
def learning_schedule(t):
return t0 / (t + t1)
np.random.seed(42)
t = 0
for epoch in range(n_epochs):
shuffled_indices = np.random.permutation(m)
X_b_shuffled = X_b[shuffled_indices]
y_shuffled = y[shuffled_indices]
for i in range(0,m,minibatch):
t+=1
xi = X_b_shuffled[i:i+minibatch]
yi = y_shuffled[i:i+minibatch]
gradients = 2/minibatch* xi.T.dot(xi.dot(theta)-yi)
eta = learning_schedule(t)
theta = theta-eta*gradients
theta_path_mgd.append(theta)
minibatch = 16
每次训练的数据集大小为16
4.三种梯度下降方式的比较
theta_path_bgd = np.array(theta_path_bgd)
theta_path_sgd = np.array(theta_path_sgd)
theta_path_mgd = np.array(theta_path_mgd)
plt.figure(figsize=(12, 6))
plt.plot(theta_path_sgd[:, 0], theta_path_sgd[:, 1], 'r-s', linewidth=1, label='SGD')
plt.plot(theta_path_mgd[:, 0], theta_path_mgd[:, 1], 'g-+', linewidth=2, label='MINIGD')
plt.plot(theta_path_bgd[:, 0], theta_path_bgd[:, 1], 'b-o', linewidth=3, label='BGD')
plt.legend(loc='upper left')
plt.axis([4.0, 10, 2.0, 6.0])
plt.show()
theta_path_bgd = np.array(theta_path_bgd)
theta_path_sgd = np.array(theta_path_sgd)
theta_path_mgd = np.array(theta_path_mgd)
这3个在上面三种的方法中存储的梯度模型参数

批量梯度下降是一条平和的蓝色曲线,而随机梯度下降是红色的曲线,绿色的就是小批量梯度下降,正常情况下我们一般选择小批量梯度,其中每次batch数量越多越好。
小批量梯度下降的优势有
-
减少计算量:小批量梯度下降法每次只计算部分样本的梯度,可以减少计算量,从而提高训练速度。
-
降低内存消耗:全样本梯度下降法需要将整个训练集都载入内存中,而小批量梯度下降法只需要载入部分样本,可以减少内存消耗。
-
更容易跳出局部极小值:由于每次只考虑部分样本的梯度,小批量梯度下降法更容易跳出局部极小值,从而达到更好的全局最优解。
-
更好的泛化能力:小批量梯度下降法在训练过程中引入了随机性,从而使得模型更具有泛化能力,能够更好地适应未知数据
三、多项式线性回归方程的实现
- 构造数据集(y=o,5*x^2+x+p)
m = 100
X = 6 * np.random.rand(m, 1) - 2
y = 0.5 * X ** 2 + X + np.random.randn(m, 1)
plt.plot(X, y, 'b.')
plt.xlabel('X_1')
plt.ylabel('y')
plt.axis([-2, 4, -5, 10])
plt.show()
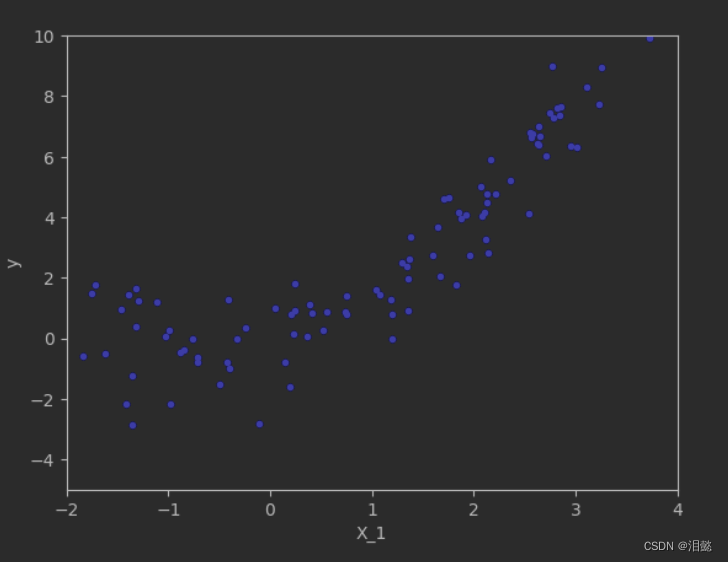
- 对特征进行多项式的扩展
from sklearn.preprocessing import PolynomialFeatures
#平方项,偏置项
poly_features=PolynomialFeatures(degree=2,include_bias=False)
X_poly=poly_features.fit_transform(X)
在机器学习中,特征的数量和质量对模型的性能有很大的影响。多项式回归就是通过对原始特征进行多项式扩展,将特征空间转换成更高维的空间,从而可以更好地拟合非线性模型。
具体来说,多项式扩展就是将原始特征进行组合,形成新的特征。例如,对于一个一元二次方程 y = ax^2 + bx + c,我们可以将 x 扩展成 [x, x^2],得到一个二元一次方程 y = a1x + a2x^2 + b,这样就将特征空间从一维扩展到了二维。
PolynomialFeatures 是一个 Scikit-Learn 库中的函数,可以用来进行多项式特征的构造。它的主要作用就是将原始特征转换成新的特征矩阵,其中每个元素是原始特征的某些次方和交叉项的乘积。这个函数可以设置 degree 参数来指定多项式扩展的次数,还可以设置 include_bias 参数来指定是否添加偏置项(即 x^0,对应于线性方程中的截距项)。
举个例子,假设原始特征是 x1 和 x2,如果设置 degree=2 和 include_bias=False,那么 PolynomialFeatures 会生成新的特征矩阵 X_poly,其中每一行对应于原始特征的某些次方和交叉项的乘积。例如,X_poly 中的第一行对应于原始特征 [x1, x2],生成的新特征为 [x1^2, x1*x2, x2^2]。这样,原始的两个特征就被扩展成了三个新特征,从而可以更好地拟合非线性模型。
- 模型
我们将特征值多项式扩展之后训练我们的模型,为了查看效果,我们生成一些测试数据,同样的操作将测试数据特征值多项式化,然后的出预测结果,画图展示
from sklearn.linear_model import LinearRegression
lin_reg=LinearRegression()
lin_reg.fit(X_poly,y)#模型训练
X_new=np.linspace(-2,2,100).reshape(100,1)
X_new_poly=poly_features.transform(X_new)
y_new=lin_reg.predict(X_new_poly)
plt.plot(X,y,'r.')
plt.plot(X_new,y_new,'b.',label='predictions')
plt.axis([-3,3,-5,10])
plt.show()
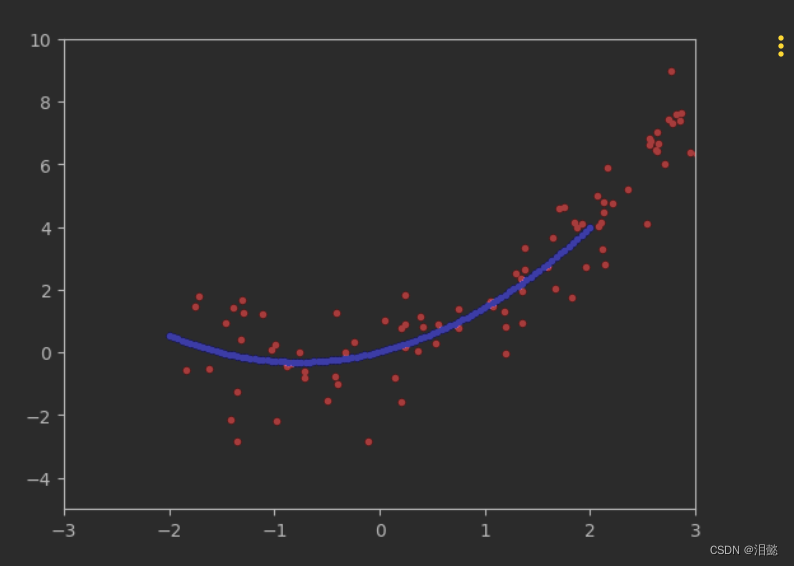
可以看到我们得出的模型还是比较拟合的。
四、标准化及特征值维度变化
在机器学习中,标准化是一种常用的预处理技术,用于将数据转换成具有标准正态分布的形式。标准化可以使得不同特征之间的值具有可比性,并且可以提高许多机器学习算法的性能,例如支持向量机、k-近邻等算法。
标准化的实现通常包括以下两个步骤:
中心化:将数据的均值移动到 0。
缩放:将数据的方差缩放到 1。
在机器学习对于多特征值,标准化可以有效的减少拟合的过程
标准化的实现通常使用 Scikit-Learn 库中的 StandardScaler 类来完成,该类可以对数据进行中心化和缩放操作,同时可以保存训练集的均值和标准差,以便后续的测试集使用相同的标准化方式。
from sklearn.preprocessing import StandardScaler
# 创建 StandardScaler 对象
scaler = StandardScaler()
# 对训练集进行标准化
X_train_scaled = scaler.fit_transform(X_train)
# 对测试集使用相同的标准化方式
X_test_scaled = scaler.transform(X_test)
为了便于操作与观察,我们继续采用上面上面多项式产生的数据集
并且比较不同特征值维度的转换带来的效果。
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
for style,width,degree in (('g-',1,100),('b--',2,2),('r-+',3,1)):
ploy_features=PolynomialFeatures(degree=degree,include_bias=False)
std=StandardScaler()
lin_reg = LinearRegression()
Polynomial_reg=Pipeline([('poly_features',ploy_features),
('StandardScaler', std),
('lin_reg',lin_reg)])
Polynomial_reg.fit(X,y)
y_new_2=Polynomial_reg.predict(X_new)
plt.plot(X_new,y_new_2,style,label='degree'+str(degree),linewidth=width)
plt.plot(X,y,'r.')
plt.axis([-3,3,-5,10])
plt.legend(loc='upper center')
plt.show()
其中Pipeline 是 scikit-learn 中的一个类,用于将多个操作流程组合在一起,形成一个完整的预处理和模型训练流程。可以在 Pipeline 中指定多个步骤,每个步骤可以是一个转换器(transformer)或者是一个估计器(estimator)。其中,转换器用于对数据进行预处理,而估计器则用于训练和预测模型。
Pipeline 的作用是将多个操作流程组合在一起,形成一个完整的预处理和模型训练流程,可以极大地简化机器学习模型的构建流程。使用 Pipeline 可以将多个数据预处理和模型训练的步骤组合成一个单独的对象,从而可以更加方便地进行模型训练和参数调整。例如,在机器学习中,通常需要对数据进行标准化处理、特征选择、模型训练等操作,使用 Pipeline 可以将这些步骤组合在一起,形成一个完整的机器学习流程,使得代码更加简洁、易于维护。
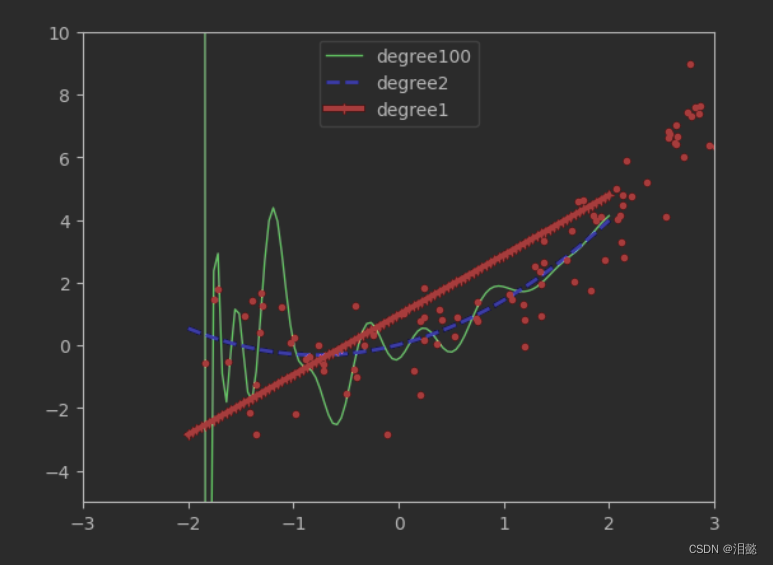
我们可以发现特征纬度值越高,其过拟合的风险越高,选择合适的维度,图中纬度值为2是最好的
五、样本数量对模型结果的影响
样本数量对机器学习的结果有着非常重要的影响。通常情况下,样本数量越多,机器学习算法就能够更好地学习数据的特征和规律,从而得到更加准确和泛化能力更强的模型。另外,增加样本数量还可以有效地避免过拟合的问题,从而提高模型的预测能力。
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
def plot_learning_curves(model, X, y):
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2, random_state=100)
train_errors, val_errors = [], []
for m in range(1, len(X_train)):
model.fit(X_train[:m], y_train[:m])
y_train_predict = model.predict(X_train[:m])
y_val_predict = model.predict(X_val)
train_errors.append(mean_squared_error(y_train[:m], y_train_predict[:m]))
val_errors.append(mean_squared_error(y_val, y_val_predict))
plt.plot(np.sqrt(train_errors), 'r-+', linewidth=2, label='train_error')
plt.plot(np.sqrt(val_errors), 'b-', linewidth=3, label='val_error')
plt.xlabel('Trainsing set size')
plt.ylabel('RMSE')
plt.legend()
lin_reg = LinearRegression()
plot_learning_curves(lin_reg, X_poly, y)
plt.axis([-1, 80, 0, 1.5])
plt.show()
这段代码中的 train_test_split 函数用于将数据集划分为训练集和验证集,其中验证集大小为总样本数的20%。然后在 plot_learning_curves 函数中,通过在不同的训练集大小下多次拟合模型并计算训练集误差和验证集误差来绘制学习曲线。对于每个训练集大小m,函数先用前m个样本来拟合模型,然后计算模型在训练集和验证集上的误差。这里使用的是均方根误差(RMSE)作为误差度量。最后,函数将训练集误差和验证集误差随着训练集大小的变化绘制成曲线,以观察模型在不同样本数量下的性能表现。
mean_squared_error是sklearn.metrics模块中的一个函数,用于计算均方误差(Mean Squared Error,MSE)。
均方误差是一种衡量回归模型拟合效果的标准,计算公式为:MSE=1n∑i=1n(yi−yi)2MSE=n1∑i=1n(yi−yi)2 其中 y i y_i yi 是真实的目标值, y ^ i \hat{y}_i y^i 是模型预测的目标值, n n n 是样本数量。
在机器学习中,我们通常会使用均方误差来衡量回归模型的预测误差,MSE的值越小,说明模型的预测结果越准确。因此,mean_squared_error的作用就是计算回归模型预测结果与真实结果之间的MSE值。
运行
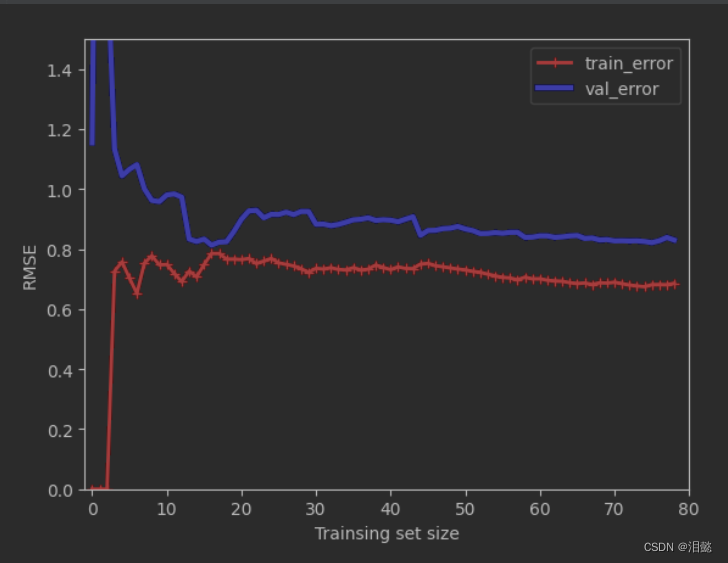
绘制出的曲线显示了随着训练集大小的增加,训练集误差和验证集误差的变化情况,从而可以用于评估模型的泛化性能,并找出是否存在欠拟合或过拟合的问题。
当两者的误差都比较大的时候,并且差距不是很大,就为欠拟合,再增加更多的训练数据对模型性能没有太大的提高。模型过拟合时,训练误差很小,但是验证误差很大,并且它们之间的差距很大,此时增加更多的训练数据可以在一定程度上缓解过拟合问题.
六、正则化
在机器学习中,正则化是一种常用的技术,用于控制模型的复杂度,防止模型过拟合。正则化通过向模型的损失函数添加一个正则项,惩罚模型的权重,从而使得模型的复杂度更小,提高泛化性能。
在线性回归中,常用的正则化方法包括L1正则化和L2正则化。L1正则化会使得一部分权重为0,因此可以用于特征选择。L2正则化会使得权重趋向于小的值,但不会将权重归零。
1.Ridge
Ridge 是 Scikit-learn 中实现岭回归的类,用于对线性回归模型进行正则化处理,以防止过拟合。
岭回归是一种改进的线性回归方法,通过对损失函数加上一个 L2 正则化项来限制模型的复杂度。Ridge 类的参数 alpha 控制着正则化项的强度,alpha 越大,正则化强度越高,模型复杂度越低。
与普通的线性回归不同,岭回归的解并不是封闭形式的,而是通过求解一个带有正则化项的优化问题得到的,因此需要使用数值优化方法进行求解。Scikit-learn 中的 Ridge 类封装了这个求解过程,提供了一些可选的求解方法,例如使用 Cholesky 分解求解、使用 L-BFGS 优化器等。同时,Ridge 类也支持使用 Pipeline 对数据进行预处理和特征提取。
from sklearn.linear_model import Ridge
np.random.seed(42)
m = 20
X = 3*np.random.rand(m,1)
y = 0.5 * X +np.random.randn(m,1)/1.5 +1
X_new = np.linspace(0,3,100).reshape(100,1)
def plot_model(model_calss,polynomial,alphas,**model_kargs):
for alpha,style in zip(alphas,('b-','g--','r.')):
model = model_calss(alpha,**model_kargs)
if polynomial:
model = Pipeline([('poly_features',PolynomialFeatures(degree =10,include_bias = False)),
('StandardScaler',StandardScaler()),
('lin_reg',model)])
model.fit(X,y)
y_new_regul = model.predict(X_new)
lw = 2 if alpha > 0 else 1
plt.plot(X_new,y_new_regul,style,linewidth = lw,label = 'alpha = {}'.format(alpha))
plt.plot(X,y,'b.',linewidth =3)
plt.legend()
plt.figure(figsize=(14,6))
plt.subplot(121)
plot_model(Ridge,polynomial=False,alphas = (0,1,10))
plt.subplot(122)
plot_model(Ridge,polynomial=True,alphas = (0,10**-5,1))
plt.show()
这段代码定义了一个函数plot_model,它用于绘制带有不同正则化参数(alpha)的岭回归模型的预测结果。具体而言,这个函数接受以下参数:
model_calss: 一个模型类,如Ridge或Lasso。
polynomial: 一个布尔值,表示是否对特征进行多项式扩展。
alphas: 一个包含正则化参数alpha的元组,用于在不同的正则化强度下训练模型。
**model_kargs: 其他模型参数。
在函数中,对于每个alpha值,都创建了一个对应的模型实例,并在需要时进行多项式扩展和标准化。然后,使用每个模型拟合数据,并使用绘图工具matplotlib将其结果可视化。最终的输出是一个包含两个子图的图形,分别显示了未经多项式扩展和经过多项式扩展的数据的结果,每个子图中有三条曲线,分别对应于不同的alpha值。
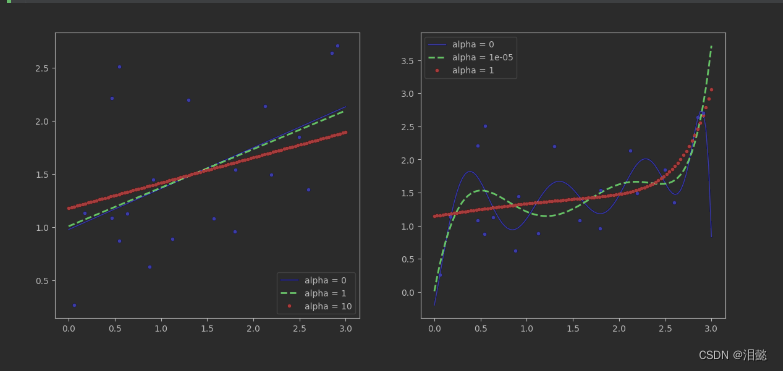
因为我们特征值是一维的,现在我们主要看右边图,经过特征值多维度扩展后不同惩罚力度的效果比较,惩罚力度越大,alpha值越大的时候,得到的决策方程越稳定,我们发现当惩罚力度为1的时候,拟合线最平稳
2.Lasso
Lasso 是一种基于 L1 正则化的线性回归模型,它的主要目标是尽可能的缩小模型的系数,从而使得一些无用特征的系数为零。在机器学习中,这种方法也被称为特征选择。与 Ridge 正则化不同的是,Lasso 正则化会使一些系数直接变为零,因此它可以用于特征选择。
Lasso 是一种线性回归的正则化方法,它通过添加一个惩罚项来限制模型的复杂度,从而防止过拟合。在训练模型时,它会将某些系数(特征)缩小甚至变为 0,从而实现特征选择的作用。
在使用 Lasso 进行线性回归时,可以通过调节正则化参数 alpha 的值来控制惩罚项的强度。当 alpha 值较小时,惩罚项的影响较小,模型更容易过拟合;当 alpha 值较大时,惩罚项的影响较大,模型更容易欠拟合。
from sklearn.linear_model import Lasso
plt.figure(figsize=(14,6))
plt.subplot(121)
plot_model(Lasso,polynomial=False,alphas = (0,1,10))
plt.subplot(122)
plot_model(Lasso,polynomial=True,alphas = (0,0.1,1))
plt.show()
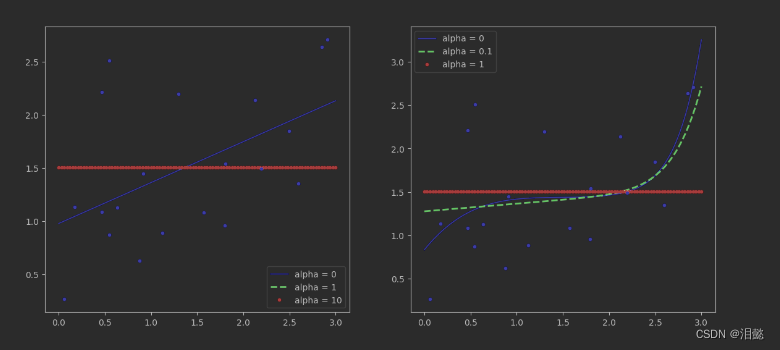
从右边的图我们可以发现,当惩罚力度为1的时候,过大,模型欠拟合。当选择为0.1的时候,最平稳
七、总结
在机器学习中,无论是线性模型还是非线性模型,我们需要选择合适的优化方法以获得最优的模型参数。常用的梯度下降法是优化模型参数的常用方式之一,其中小批量梯度下降法是一种高效的优化方法,每次选择小批量的数据进行计算,可以减少计算量,提高模型的训练速度。
在多特征、多维度数据集的模型训练中,我们通常需要对数据进行标准化,将数据集中的每个特征进行归一化处理,以便能够更快地收敛到最优解,并且能够有效地避免因数据量级不同而造成的拟合问题。
样本数量对于机器学习模型的性能有很大的影响,理论上来说,样本数量越多,模型的泛化能力越好,能有效地避免过拟合的问题,从而提高模型的预测能力。
对于过于复杂的模型,我们可以使用正则化来有效地减少模型的复杂性,从而避免过拟合的情况。正则化方法可以通过惩罚模型参数的大小来限制模型的复杂程度,使其更加鲁棒,并且能够更好地适应未知数据。常用的正则化方法包括L1正则化(Lasso)和L2正则化(Ridge)。
- 由于本人水平学习能力有限,对于上述出现的错误,欢迎大家指正
希望大家多多支持,后续会分享更多新奇有趣的东西