最小二乘拟合平面——拉格朗日乘子法

一、算法原理

  设拟合出的平面方程为：
$$ax+by+cz+d=0\text{\hspace{1em}(1)}$$
约束条件为：$$a^2+b^2+c^2=1\text{\hspace{1em}(2)}$$
  可以得到平面参数 $a、b、c、d$。此时，要使获得的拟合平面是最佳的，就是使点到该平面的距离的平方和最小，即满足：
$$e=\sum _{i=1}^n{d}_i^2\to min\text{\hspace{1em}(3)}$$
  式中，$d_i=|a{x}_i+b{y}_i+c{z}_i+d|$，是点云数据中的任一点$p_i(x_i,y_i,z_i)$到这个平面的距离。要使$e\to min$，可以利用拉格朗日乘子法求解极值，得到函数：
$$f=e-\lambda (a^2+b^2+c^2-1)=\sum _{i=1}^n{d}_i^2-\lambda (a^2+b^2+c^2-1)\text{\hspace{1em}(4)}$$

  先将式(2-4)两边对$d$求偏导，并且令偏导数为零，得到：
$$d=\frac{1}{n}(a\sum _{i=1}^n{x}_i^2+b\sum _{i=1}^n{y}_i^2+c\sum _{i=1}^n{z}_i^2)\text{\hspace{1em}(5)}$$
令$\bar{x}={\sum }_{i=1}^n\frac{x_i}{n}$、$\bar{y}={\sum }_{i=1}^n\frac{y_i}{n}$、$\bar{z}={\sum }_{i=1}^n\frac{z_i}{n}$，质心为$\bar{P}=(\bar{x},\bar{y},\bar{z})$，$\Delta x_i=x_i-\bar{x}$，$\Delta y_i=y_i-\bar{y}$，$\Delta z_i=z_i-\bar{z}$则：
$$d_i=|a\Delta x_i+b\Delta y_i+c\Delta z_i|\text{\hspace{1em}(6)}$$
  再对式(2-4)两边求对$a、b、c$ 的偏导数，得
$$\{\begin{array}{l}2{\sum }_{i=1}^n(a\Delta x_i+b\Delta y_i+c\Delta z_i)\Delta x_i-2\lambda a=0\\ 2{\sum }_{i=1}^n(a\Delta x_i+b\Delta y_i+c\Delta z_i)\Delta y_i-2\lambda b=0\\ 2{\sum }_{i=1}^n(a\Delta x_i+b\Delta y_i+c\Delta z_i)\Delta z_i-2\lambda c=0\end{array}$$

  将上述方程组构成特征值方程：
$$Ax=\lambda x\text{\hspace{1em}(7)}$$
式中，
$$A=\left[\begin{array}{ccc}{\sum }_{i=1}^n\Delta x_i^2& {\sum }_{i=1}^n\Delta x_i\Delta y_i& {\sum }_{i=1}^n\Delta x_i\Delta z_i\\ {\sum }_{i=1}^n\Delta x_i\Delta y_i& {\sum }_{i=1}^n\Delta y_i^2& {\sum }_{i=1}^n\Delta y_i\Delta z_i\\ {\sum }_{i=1}^n\Delta x_i\Delta z_i& {\sum }_{i=1}^n\Delta y_i\Delta z_i& {\sum }_{i=1}^n\Delta z_i^2\end{array}\right]$$
$$x=\left[\begin{array}{c}a\\ b\\ c\end{array}\right]$$
  那么，求解平面参数$a、b、c$ ，就是求解矩阵的特征值和特征向量。又因为$A$ 是3 阶实对称矩阵，其特征值求解公式为：
$$\lambda =\frac{(Ax{)}^{T}x}{x^{T}x},x\ne 0\text{\hspace{1em}(8)}$$
  在约束条件$a^2+b^2+c^2=1$ 下，得$\lambda ={\sum }_{i=1}^n(a\Delta x_i+b\Delta y_i+c\Delta z_i{)}^2={\sum }_{i=1}^n{d}_i^2=e$。 所以，$e$最小值就是矩阵$A$的最小特征值，对应特征向量为平面参数$a、b、c$ ，利用质心可求得$d$。

二、代码实现

1、python

import numpy as np


# 创建函数，用于生成不同属于一个平面的100个离散点
def not_all_in_plane(a, b, c):
    x = np.random.uniform(-10, 10, size=100)
    y = np.random.uniform(-10, 10, size=100)
    z = (a * x + b * y + c) + np.random.normal(-1, 1, size=100)
    return x, y, z


# 调用函数，生成离散点
x, y, z = not_all_in_plane(2, 5, 6)
# 计算质心
x0 = np.mean(x)
y0 = np.mean(y)
z0 = np.mean(z)
# 去质心
x = x - x0
y = y - y0
z = z - z0
# ------------------------构建系数矩阵-----------------------------
A = np.array([[sum(x * x), sum(x * y), sum(x * z)],
              [sum(x * y), sum(y * y), sum(y * z)],
              [sum(x * z), sum(y * z), sum(z * z)]])
[D, X] = np.linalg.eig(A)

print('平面拟合结果为：z = %.3f * x + %.3f * y + %.3f' % (X[0, 2], X[1, 2], X[2, 2]))

2、matlab

clc;clear;
%% -------------------------------读取点云---------------------------------
pc = ReadPointCloud('plane1.pcd');
%% -----------------------------获取点云信息-------------------------------
n ; % 点的个数
x ; % 点的x坐标
y ; % 点的y坐标
z ; % 点的z坐标
% 1、计算点云质心
centroid = pcmean(pc);
% 2、去质心化
deMean=pcdemean(pc.Location,centroid);
%% -------------------------------拟合平面---------------------------------
% 3、矩阵A
A = [sumXX sumXY sumXZ;
	sumXY sumYY sumYZ;
	sumXZ sumYZ sumZZ];
% 4、矩阵A分解求特征值特征向量
[V,D]=eig(A);
a = V(1,1);b = V(2,1);c = V(3,1);
% 5、计算原点到拟合平面的距离
d = -dot([a b c],centroid);
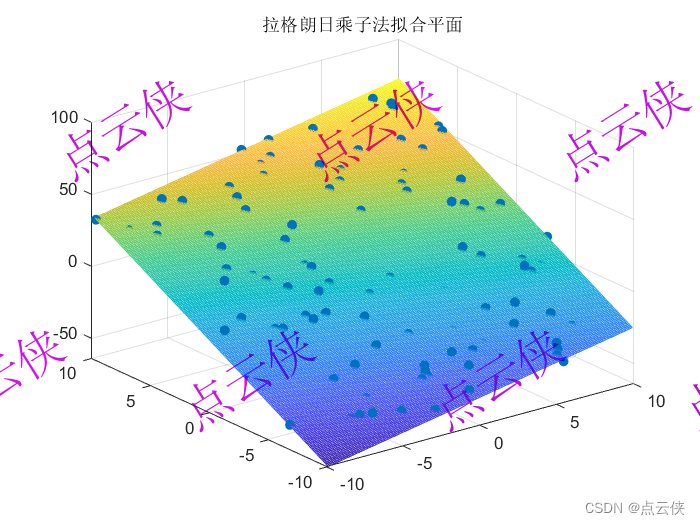
%% ---------------------------可视化拟合结果-------------------------------
 figure
% 图形绘制
scatter3(x,y,z,'filled')
hold on;
[XFit,YFit]= meshgrid (xfit,yfit);
mesh(XFit,YFit,ZFit);
title('拉格朗日乘子法拟合平面');

三、算法效果