用四元数或 DCM Matrix 表示旋转

英文版参考链接:Quaternions

DCM matrix

DCM matrix是一个用来描述两个坐标系之间的转换的矩阵。如果我们把第一个坐标系记为x，第二个坐标系记为y，那么DCM matrix就是一个3x3的矩阵，它的每一列是y坐标系的一个单位向量在x坐标系下的表示。

$DCM^{B} = (DCM^G)^T$ or $DCM^G = (DCM^B)^T$

且

DCM 矩阵（通常也称为旋转矩阵）定义了一个框架相对于另一框架的旋转。如果我们知道任意向量在B框架中的坐标（反之亦然），它也可以用于确定任意向量在全局框架中的坐标。

a vector with body coordinates:

如果我们知道两个坐标系之间的旋转角度，比如偏航角（yaw）、俯仰角（pitch）和滚转角（roll），那么我们可以用一些数学公式来计算出DCM matrix。这些公式取决于旋转的顺序，比如先绕z轴旋转偏航角，再绕y轴旋转俯仰角，最后绕x轴旋转滚转角。这种顺序可以记为ZYX。那么对应的DCM matrix可以写成

intrinsic rotation和extrinsic rotation的区别是，前者是指绕着旋转后的坐标系的轴进行旋转，后者是指绕着固定的坐标系的轴进行旋转。例如，如果我们用ZYX顺序来表示旋转，那么intrinsic rotation就是先绕着x轴旋转滚转角（roll），然后绕着新的y轴（y′）旋转俯仰角（pitch），最后绕着新的z轴（z″）旋转偏航角（yaw）。而extrinsic rotation就是先绕着z轴旋转偏航角，然后绕着原来的y轴旋转俯仰角，最后绕着原来的x轴旋转滚转角。

四元数

旋转四元数的性质:

All rotation quaternions must be unit quaternions.|q| = 1
For rotation quaternions, the inverse equals the conjugate. So for rotation quaternions, q−1 = q* = ( q0, −q1, −q2, −q3 ).
如果一个点p用q旋转后变成了p’，那么再用q−1或者q*旋转p’，就会变回p。这是因为两次旋转相互抵消了
A rotation of qa followed by a rotation of qb can be combined into the single rotation qc = qbqa.

将四元数转换为旋转矩阵

将旋转矩阵转换为四元数

将欧拉角转换为四元数

θ (theta) y
φ (phi) x
ψ (psi) z

约定:

固有旋转（轴随着每次旋转而移动）
主动（也称为 alibi）旋转（旋转的是点，而不是坐标系）
具有右手旋转的右手坐标系

ZXY顺序的欧拉角z,x,y对应的四元数q为：

$R = R_{z}(\theta_{z})R_{x}(\theta_{x})R_{y}(\theta_{y}) = \begin{bmatrix} \cos\theta_{z} & -\sin\theta_{z} & 0 \\ \sin\theta_{z} & \cos\theta_{z} & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos\theta_{x} & -\sin\theta_{x} \\ 0 & \sin\theta_{x} & \cos\theta_{x} \end{bmatrix} \begin{bmatrix} \cos\theta_{y} & 0 & \sin\theta_{y} \\ 0 & 1 & 0 \\ -\sin\theta_{y} & 0 & \cos\theta_{y} \end{bmatrix} = \begin{bmatrix} \cos{\theta_y}\cos{\theta_z}-\sin{\theta_x}\sin{\theta_y}\sin{\theta_z} & -\cos{\theta_x}\sin{\theta_z} & \cos{\theta_z}\sin{\theta_y}+\cos{\theta_y}\sin{\theta_x}\sin{\theta_z}\\ \cos{\theta_y}\sin{\theta_z}+\cos{\theta_z}\sin{\theta_x}\sin{\theta_y}& \cos{\theta_x}\cos{\theta_z}& \sin{\theta_z}\sin{\theta_y}-\cos{\theta_z}\cos{\theta_y}\sin{\theta_x}\\ -\cos{\theta_x}\sin{\theta_y}& \sin{\theta_x}& \cos{\theta_x}\cos{\theta_y} \end{bmatrix}$

$\theta_x = \arcsin(m_{32})$

= np.arcsin(2q2*q3 + 2q0*q1)

$\theta_{y}=\tan^{-1}\left(\begin{array}{c}{\frac{-m_{31}}{m_{33}}}\\\end{array}\right)$

=np.arctan2(

2q0q2 - 2q1q3
--------------------
1 - 2q1q1 - 2q2q2

)

$\theta_{z}=\tan^{-1}\left(\frac{-m_{12}}{m_{22}}\right)$

= np.arctan2(

2*q0*q3 - 2*q1*q2
---------------------------
1 - 2*q1*q1 - 2*q3*q3

)

而ZYX顺序的欧拉角z,y,x对应的四元数q为：

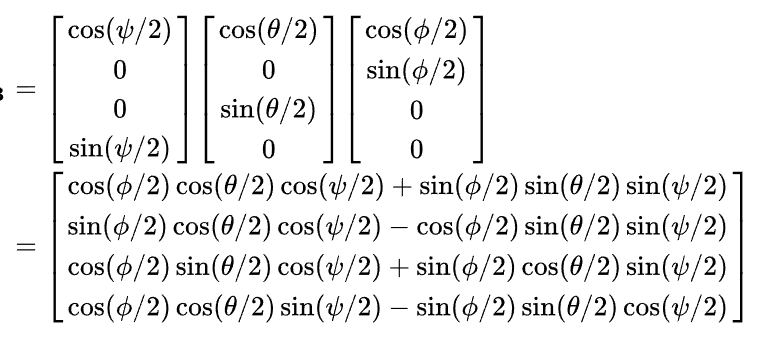
ZYX顺序的欧拉角z,y,x，表示先绕着固定坐标系的z轴旋转z角度，然后绕着旋转后的y轴旋转y角度，最后绕着旋转后的x轴旋转x角度。这里的z,y,x都是相对于固定坐标系的角度，而不是相对于旋转后的坐标系的角度。也就是说，z是初始状态下的偏航角（yaw），y是初始状态下的俯仰角（pitch），x是初始状态下的滚转角（roll）。