基于四元数的旋转理解

一、复数

首先介绍复数的思路（虚数为复数的一部分）

而复数平面的创建并不是由上述的定义直观得来的，而是人们发现用复数系统来描述平面由以下优越性：

1.用复数形式表示二维坐标的时候，保留了横轴和纵轴的坐标信息。

2.虚数i可以表示90度旋转。

3.当把复数平面中某个点绕原点旋转时，可以用一个复数来表示旋转角度 

二、四元数

扫描二维码关注公众号，回复： 2555569 查看本文章

2.1四元数的定义及运算法则

“四元数的运算有乘积、点乘，没有定义叉乘。而四元数乘积中利用到四元数的 哈密顿定义式   ，而在四元数乘积简化表达式中利用到了    向量的点乘和叉乘  ”

2.2利用单位四元数对三维空间内的点进行旋转

当然一般的四元数也可以旋转，但利用单元四元数是为了使旋转后该点的模不变，或者说到原点的距离不变。

十九世纪的汉密尔顿也许确实不知道内积和外积，但是他知道，他想要的三维向量乘法要比内积和外积运算“高大上”很多。这一乘法运算要满足下列四条性质：（）
1.运算产生的结果也要是三维向量
2.存在一个元运算，任何三维向量进行元运算的结果就是其本身
3.对于任何一个运算，都存在一个逆运算，这两个运算的积是元运算
4.运算满足结合律

换而言之，汉密尔顿想定义的不是一个简单的映射关系，而是一个群！（后来我们知道四元数所在群为S3，而四元数所代表的三维旋转是SO(3)，前者是后者的两倍覆盖）内积连性质1都不满足（向量内积得到标量），外积不满足性质3（任意两个向量外积都不能得到其中一个的本身，因为外积符合右手定则，要么得到一个垂直于两个外积向量的向量，要么这两个向量平行 时外积得到零向量 ）。

其实，四元数有四个变量，完全可以被看作一个四维向量。，四元数乘以四元数其实看作（1）对进行左旋转，或者（2）对进行右旋转。所以从始至终，四元数定义的都是四维旋转，而不是三维旋转！任意的四维旋转都可以唯一的拆分为一个左旋转和一个右旋转，表达出来就是。这里，我们对四元数（四维向量）进行了一个左旋转和一个右旋转。结果当然是一个四元数，符合性质1。这个运算也同时符合性质2，3，4。（单位四元数（norm=1）则存在于四维空间的一个球面上。）

好了，说完了四维旋转，我们终于可以说说三维旋转了。说白了，三维旋转就是四维旋转的一个特例，就像二维旋转是三维旋转的一个特例一样。说是特例其实不准确，准确的说是一个子集或者subgroup。为了进行三维旋转运算，汉密尔顿首先在四维空间里划出了一块三维空间。汉密尔顿定义了一种纯四元数（pure quaternion），其表达式为。纯四元数第一项为零，它存在于四维空间的三维超平面上，与三维空间中的三维向量一一对应。然后，就有了我们常见的这种左乘单位四元数，右乘其共轭的表达式。我真心不知道汉密尔顿是怎么想出来的，不过回过头来看，这个运算形式是为了限制其运算结果所在的空间。简单的说，当对一个三维向量进行三维旋转后，我们希望得到的是一个三维向量。（如果你真能得到一个四维向量，就不敢自己在家转圈圈了吧，转着转着，就进入四次元了！）那么这个左乘单位四元数，右乘其共轭的运算保证了结果是一个在三维超平面上中的纯四元数。

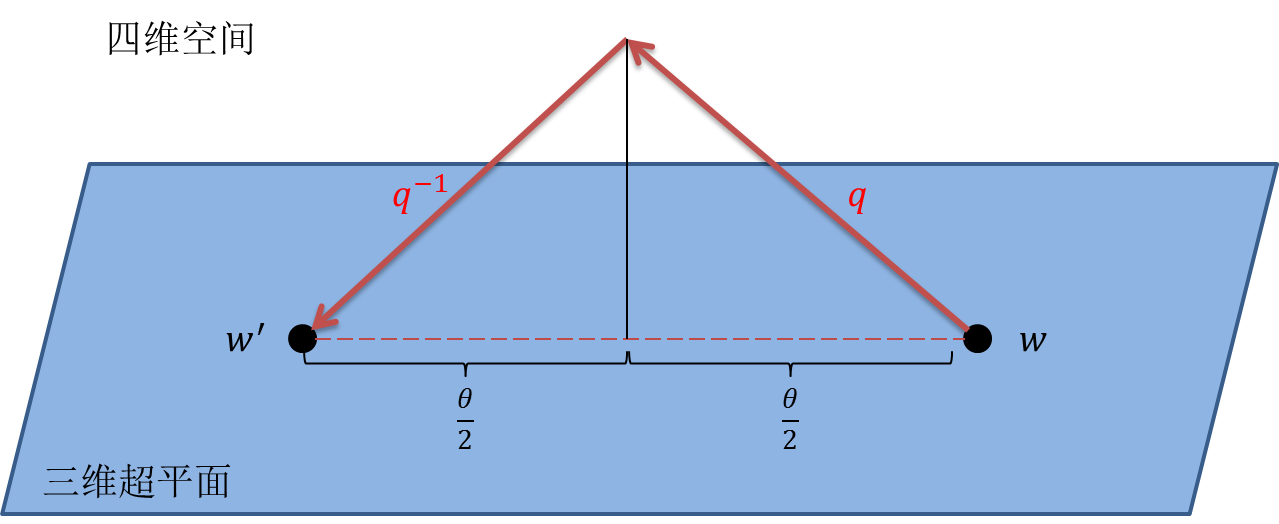
其实这张图解释了一个长久的疑问。为什么四元数里用的是而不是。这是因为做的就是一个的旋转，而也做了一个的旋转。我们进行了两次旋转，而不是一次。第一次旋转将三维超平面的点旋转出了该平面，第二次又把这个点旋回到该平面。这两次旋转的结果是一个旋转角为的旋转。

转载：

1.http://www.qiujiawei.com/understanding-quaternions/#4.3

2.https://www.zhihu.com/question/23005815/answer/33971127

3.http://www.qiujiawei.com/understanding-quaternions/#4.3