旋转矩阵:
1.旋转矩阵是正交矩阵,矩阵的每一行每一列的模,都为1;并且任意两个列向量或者任意两个行向量都是正交的。
2. 矩阵的行列式为1。矩阵的逆和转置是相等的。
什么是旋转矩阵?如图1所示,我们假设最开始空间的坐标系,
,
就是笛卡尔坐标系,这样我们得到空间A的矩阵
={
,
,
}T,其实也可以看做是单位阵E。进过旋转后,空间A的三个坐标系变成了图1中红色的三个坐标系
,
,
,得到空间B的矩阵
={
,
,
}T。我们将两个空间联系起来可以得到
=R•
,这里R就是我们所说的旋转矩阵。

由于={1,0,0}T,
={0,1,0}T,
={0,0,1}T,结合图2可以看出,旋转矩阵R就是由
,
,
三个向量组成的(因为
是单位阵)。因为单位向量无论怎么旋转长度肯定不会变而且向量之间的正交性质也不会变。那么旋转矩阵就是正交阵!如下式所示。
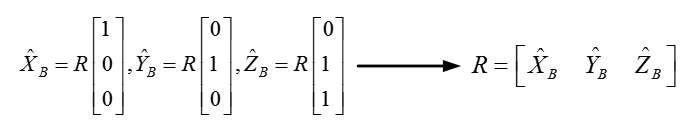
接下来就是重点了,我们结合图4进行分析。由于旋转矩阵R就是由,
,
三个向量组成的。我们来看看
,
,
究竟是什么?由于图中所有的向量均是单位向量,所以
与
点乘的结果可以看成
在
上的投影的模,也就是
在空间A中x轴的分量!!图中中间的位置列出了
向量中的三个分量分别为
在
上的投影的模、
在
上的投影的模和
在
上的投影的模。这从几何角度很好理解。以此类推,可以得出的旋转矩阵R的表达形式。我们根据图4可以惊喜的发现,矩阵R的第一行就是
在
,
,
上的投影的模,也就是
。

如图6所示为例,由于绕x轴旋转,所以我们观察,
分别在
和
上的投影情况。旋转矩阵的每一列表示旋转后的单位向量方向,旋转矩阵相当于把一个向量(空间)旋转成新的向量(空间)

根据旋转前后的向量求旋转矩阵
1.旋转角度

2.旋转轴旋转角所在的平面为有P和Q所构成的平面,那么旋转轴必垂直该平面。假定旋转前向量为a(a1, a2, a3), 旋转后向量为b(b1, b2, b3)。通过叉乘可求得
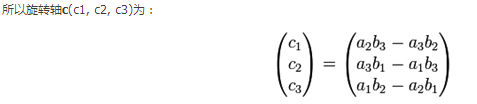
四元数
四元数的一个最主要的应用就是表示旋转,它既是紧凑的,也没有奇异性。在讲四元素之前,先来看下简单的欧拉角和轴向角。
欧拉角使用最简单的x,y,z值来分别表示在x,y,z轴上的旋转角度,其取值为0-360(或者0-2pi),一般使用roll,pitch,yaw来表示这些分量的旋转值。需要注意的是,这里的旋转是针对世界坐标系说的,这意味着第一次的旋转不会影响第二、三次的转轴。欧拉角容易出现的问题是 1)不易在任意方向的旋转轴插值; 2)万向节死锁;3)旋转的次序无法确定。
轴角用一个以单位矢量定义的旋转角,再加上一个标量定义的旋转角来表示旋转。通常的表示[x,y,z,theta],前面三个表示轴,最后一个表示角度。但是轴角形式的旋转不能直接施于点或矢量,必转换为矩阵或者四元素。四元素感觉上就是轴角的进化,也是使用一个3维向量表示转轴和一个角度分量表示绕此转轴的旋转角度,即(x,y,z,w),观察四维单位超球面在三维的投影,可以对它有个更深入的了解。(见文末链接)
四元数:
1.一个四元数包含一个标量分量和一个3D向量分量。记标量为w,记向量为v或分开的x,y,z。如下:[w,v]即[w,(x,y,z)]。注意:单位四元素才能描述旋转,所以四元素使用前必须归一化:q.normalize()。
![]()
2.四元数扩展了复数系统 ,它使用三个虚部i,j,k。它们的关系如下:
ij=k,ji=-k;jk=i,kj=-i;ki=j,ik=-j
一个四元数[w,(x,y,z)]定义了复数 w+xi+yj+zk。对于i、j、k本身的几何意义可以理解为一种旋转,其中i旋转代表X轴与Y轴相交平面中X轴正向向Y轴正向的旋转,j旋转代表Z轴与X轴相交平面中Z轴正向向X轴正向的旋转,k旋转代表Y轴与Z轴相交平面中Y轴正向向Z轴正向的旋转,-i、-j、-k分别代表i、j、k旋转的反向旋转
3.四元数和轴-角对:四元数能被解释为角位移的轴-角对方式。设向量n为旋转轴,θ为绕轴旋转的量。
q=[cos(θ/2) sin(θ/2)n]=[cos(θ/2) (sin(θ/2)nx sin(θ/2)ny sin(θ/2)nz)]
(用一个旋转轴n和旋转角θ来描述一个旋转,所以也称轴角。不过很明显,因为旋转角度有一定的周期性(360°一圈),所以这种表达方式具有奇异性。从旋转向量到旋转矩阵的转换过程称为 罗德里格斯公式)
4.如何用四元数将3D点绕轴旋转:
让我们“扩展”一个标准3D点(x,y,z)到四元数空间,通过定义四元数p=[0, (x,y,z)]即可。设q为我们讨论的旋转四元数形式[cos(θ/2) sin(θ/2)n],n为旋转轴单位向量,θ为旋转角。执行下面乘法可使3D点p绕n旋转:p'=qp.
为什么我们用 qp的方法表示三维旋转,其中 p 是表示三维空间向量的纯四元数。首先,如果待旋转的向量 p 与单位四元数虚部所表示的旋转轴正交时,我们只需要左乘单位四元数就可以表示此旋转。如下图所示,i 点绕 k 轴进行旋转,左乘单位四元数 q 即可。可是对于大部分情况,向量 p 和旋转轴并不正交,单单只是左乘单位四元数 q 会在三维空间中有拉伸的效果。注意整个三维空间都是单位超球面的投影,这里的拉伸只不过是投影之后的一种效果罢了。我们用四元数并不关心四维单位超球面的旋转,而是拿它来描述三维空间的旋转,于是我们必须要找到一种不带拉伸效果的四元数运算。人们发现,当右乘 q 的逆时,同方向的旋转会继续进行,而拉伸的效果互相抵消,于是就有了 qp
. 的表示方法。
5.四元数的乘法和求逆
乘法:给定两个四元数p和q,分别代表旋转P和Q,则乘积pq表示两个旋转的合成(即旋转了Q之后再旋转P)。四元数的乘法定义如下,利用简单的分配律就是了:
q1 * q2 =(w1*w2 - x1*x2 - y1*y2 - z1*z2) +
(w1*x2 + x1*w2 + y1*z2 - z1*y2) i +(w1*y2 - x1*z2 + y1*w2 + z1*x2) j +(w1*z2 + x1*y2 - y1*x2 + z1*w2) k
由于q = w + x i + y j + z k中可以分为纯量w与向量x i + y j + z k,所以为了方便表示,将q表示为(S, V),其中S表示纯量w,V表示向量x i + y j + z k,所以四元数乘法又可以表示为:
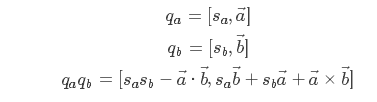
求逆:对于向量逆的定义, q-1 =q*/|q|2
对于单位四元素,分母为1,q-1 = q* =(-x, -y, -z, w)
6.四元素转化为旋转矩阵Matrix(3*3):
1- 2*y*y - 2*z*z, 2x*y - 2*z*w, 2*x*z + 2y*w
2*x*y + 2*z*w, 1 - 2*x*x - 2*z*z, 2*y*z - 2*x*w
2*x*z - 2*y*w, 2*y*z + 2*x*w, 1 - 2*x*x - 2*y*y
补充:
四元数推导
对于一个复数p=a+bi,将它旋转角度θ,先定义另外一个复数q=cosθ+isinθ,我们发现,复数的乘法表示了一种旋转:
qp=(acosθ−bsinθ)+i(asinθ+bcosθ)。这个复数恰好就是p旋转θ角度后的值。
看到了二维复数乘法可以表示旋转,那么三维空间呢,我们会想到再增加一个虚数作为第三个维度,我们定义两个个三维的复数:
z1=a1+b1i+c1j,z2=a2+b2i+c2j
我们类似的进行复数的乘法,得到:
![]()
我们会发现,如果没有ij和ji这两项,我们三维的复数旋转也就没问题,那该如何处理呢,哈密尔顿引入四维的四数:q=q0+q1i+q2j+q3k,根据向量的叉乘可以定义下列一些关系(ij=-ji=k,是根据右手定则):
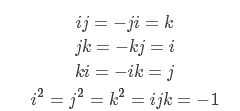


但是上面的旋转是有缺点的,因为其限制了我们的旋转轴和需要被旋转的四元数必须是垂直的(a⃗ ⋅b⃗ =0a→⋅b→=0),而不能达到任意的旋转.这时,聪明的哈密尔顿发现,一个四元数会把一个纯四元数拉到四维空间,但它的共轭又会把这个四维的空间拉回到三维空间。
![]()
from:https://blog.csdn.net/qq_28773183/article/details/80083607
from:http://www.cnblogs.com/caster99/p/4703033.html
from:http://www.zhuanzhi.ai/document/4d26b5d97249ca81129901ae7cd34a6c