揭秘logistic 回归 与 sigmoid激活函数的关系
这一期博客,博主谈谈logistic 回归在做分类任务时与sigmoid的关系,不过以下更多是探讨。
在谈这个关系之之前,我们可能需要聊很多。
首先,我们知道logistic 回归可以做分类任务,而且一般都是做分类任务,那么为什么会出现logistic 回归来做分类任务这个想法呢?
说到这个,我们要谈到线性模型做分类任务:
这里说的线性模型就是机器学习中的线性模型,线性模型的一般表示方法如下:
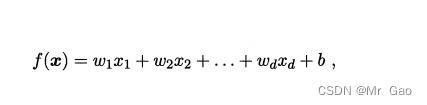
大家有一点机器学习基础的,肯定知道上面这个数学公式什么意思。
那么线性模型用向量表示如下:
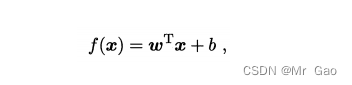
那么线性模型怎么做分类任务,一开始一些研究者就认为,线性模型一般虽然是做回归的,但是,哎,做分类也可以哎,那怎么做呢:
如下图:
注:下述样本空间指样本所在的特征空间。
人们发现,线性模型可以表示一个样本空间中的一个超平面,这个线性空间可以将样本空间一分为二,研究者就说,我们可以求一个最好的超平面,正好把我们的训练集给分好类,这不就好了嘛,那这个线性模型表示的超平面不就对进行分类了吗?
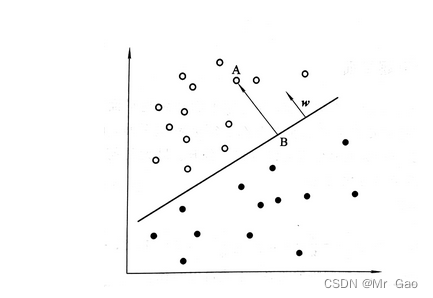
于是人们就在想,怎么样可以求得最好的超平面呢?
这个时候就是定义损失函数了,人们就定义了下面的损失函数(以二分类为例):
f ( x , w , b ) = ∑ ( w x + b ) / ∣ ∣ w ∣ ∣ ∗ ( − y ) f(x,w,b)=\sum(wx+b)/||w||*(-y) f(x,w,b)=∑(wx+b)/∣∣w∣∣∗(−y)
y的取值集合为{-1,1}
人们就说,对于正样本,我让(wx+b)/||w||>0,对于负样本,我让(wx+b)/||w||<0,
(wx+b)/||w||是样本到超平面的距离,那就是正样本让他们到超平面一边,负样本到超平面一边,然后距离超平面越远越好。
这个时候问题来了?
我们来看下面一张图:
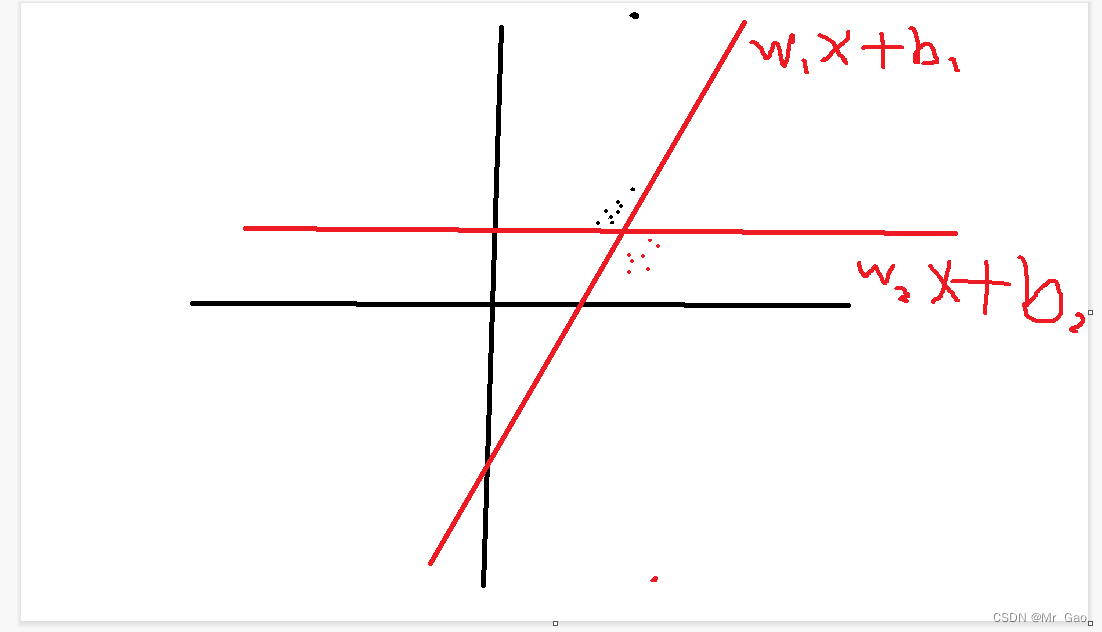
上面一张图两个线性模型都可以达到正确分类的效果,但是我们可以发现,根据我们上面损失函数训练出来的是 w 2 x + b 2 w_{2}x+b_{2} w2x+b2
但是显然是不合理的,按照图像的规律其实 w 1 x + b 1 w_{1}x+b_{1} w1x+b1应该是更合适的,这是因为,上述使用距离之和作为损失结果,但是显然有些样本如果比较离群,那么他计算得到的距离就会很大,对于损失函数的影响很大,人们想到了什么呢?
能不能对样本到超平面的距离做一个约束,这样比较离群的样本就不会那么干扰模型了,于是logistic 回归诞生了,对这个距离用sigmoid函数处理,距离不就变成0-1之间了吗?
先说一下sigmoid函数:
公式:
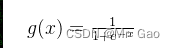
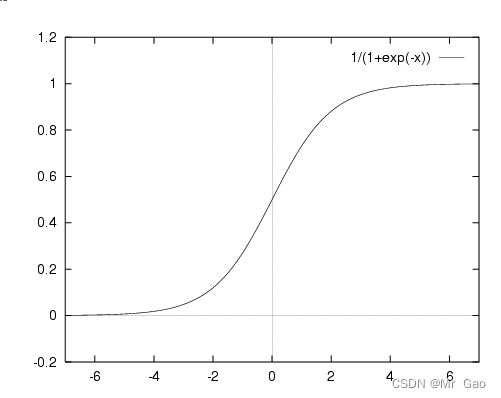
大家看上面的图,发现sigmoid函数从3->正无穷开始就几乎趋于1了,从-3->负无穷开始几乎就趋于0了,这是一个很棒的性质,通过专业这样的方法,我们就可以抵消极端样本距离对模型的影响:
比如 ( w x 1 + b ) / ∣ ∣ w ∣ ∣ = 1000 , ( w x 2 + b ) / ∣ ∣ w ∣ = 6 (wx_{1}+b)/||w||=1000, (wx_{2}+b)/||w|=6 (wx1+b)/∣∣w∣∣=1000,(wx2+b)/∣∣w∣=6
x 1 , x 2 x_{1},x_{2} x1,x2是不是经过sigmoid转化都变成1了,距离之间的巨大影响就被抵消了。所以sigmoid不是为了概率转化,他是激活函数,更多的是让模型关注样本分布的总体趋势,减小极端样本对模型的影响。
但是现在很多人都是分析sigmoid是概率转化,转化到0-1区间,其实,这个本身也是一方面,但是还是要强调sigmoid是激活函数,它的作用用于距离影响抵消是更合理的,然后人们又把问题转化为了概率问题,样本概率求解公式就如下:
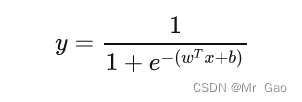
最后问题变成了概率问题也更加合理,但是sigmoid函数在最开始用于该分类问题的时候,绝不是为了概率转化那么简单,而是为了抵消样本之间距离超平面的距离差异,使得模型更加注重样本分布的总体规律。