Logistic回归

Logistic回归为概率型非线性回归模型，是研究观察结果与一些影响因素之间关系的一种多变量分析方法。

虽然名字中带有“回归”二字，但是它是一种常见的分类问题的方法。

设条件慨率 $P(y=1 | x)=p$ 为根据某自变量相对于某事件发生的概率。

Logistic回归模型为：

$P(y=1 | x)=\frac{1}{1+e^{-g(x)}}$

这里 $f(x)=\frac{1}{1+e^{-x}}$ 称为sigmoid函数，其中 $g(x)=w_{0}+w_{1} x_{1}+\ldots+w_{n} x_{n}$ 。

为什么要用sigmoid函数？

扫描二维码关注公众号，回复： 8938138 查看本文章

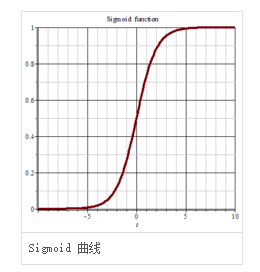
（1）从sigmoid函数本身理解

sigmoid函数如图所示，由于Logistic回归为一个概率问题，需要将值约束在0-1范围之内，因此使用了sigmoid函数，使其约束在0-1范围之内。

为什么不用阶跃函数？

阶跃函数：

$f(x)=\left\{\begin{array}{ll}{1} & {x \geq 0} \\ {0} & {x<0}\end{array}\right.$

因为在x=0处不可导，无法利用梯度下降法等求导方法，因此不使用这种函数。

（2）从概率分布角度理解

Logistic回归按照概率分布的角度，其密度函数，可以写成如下形式：

$f(x | p)=\left\{\begin{array}{ll}{p^{x} q^{1-x}} & {x=0,1} \\ {0} & {x \neq 0,1}\end{array}\right.$

即

$p(y | x, p)=p^{y}(1-p)^{1-y}$

上述这个分布是伯努利分布，而伯努利分布是指数分布簇中的一个分布；Logistic分布属于广义线性模型中的一种，因此可以从指数分布簇如果满足三个条件，就可以推出广义线性模型。从这个角度出发，来看一下哪部分是sigmoid函数。

$p(y | x, p)=\exp \left\{\log p^{y}(1-p)^{1-y}\right\}$

$=\exp \{y \log p+(1-y) log(1-p)\}$

$=exp\left \{ y \log \frac{p}{1-p}+\log (1-p)\right \}$

对比指数分布簇：

$p(y | x;\eta)=b(y)\exp\left \{ \eta T(y)-a(\eta) \right \}$

可得：

$b(y)=1$

$\eta=\log \frac{p}{1-p}$

$T(y)=y$

$a(\eta)=\log (1-p)$

由广义线性模型的三条假设：

可知：

（1）Logistic的分布服从伯努利分布，因此指数分布，参数为p

（3） $\eta$ 与x为线性关系，即 $\eta=\theta^{T} X$

由于 $\eta=\log \frac{p}{1-p}$ ，故 $p=\frac{1}{1+e^{-\eta }}$

将 $\eta=\theta^{T} X$ 带入，即有 $p=\frac{1}{1+e^{-(\theta^{T} X) }}$ ，从这可以看出sigmoid函数的形式。

（2）条件二也是很容易得出的，

$h_{p}(x)=\frac{1}{1+e^{-y}}=\frac{1}{1+e^{-\theta^{T} x}}=E[y | x ;p]$

Logistic模型参数求解

利用极大似然函数估计模型参数：

设： $p(Y=1 | x)=\pi(x), \quad p(Y=0 | x)=1-\pi(x)$

似然函数为：

$\prod_{i=1}^{N}\left[\pi\left(x_{i}\right)\right]^{n}\left[1-\pi\left(x_{i}\right)\right]^{1-x_{i}}$

对数似然函数为：

$\begin{aligned} L(w) &=\sum_{i=1}^{N}\left[y_{i} \log \pi\left(x_{i}\right)+\left(1-y_{i}\right) \log \left(1-\pi\left(x_{i}\right)\right)\right] \\ &=\sum_{i=1}^{N}\left[y_{i} \log \frac{\pi\left(x_{i}\right)}{1-\pi\left(x_{i}\right)}+\log \left(1-\pi\left(x_{i}\right)\right)\right] \\ &=\sum_{i=1}^{N}\left[y_{i}\left(w \cdot x_{i}\right)-\log \left(1+\exp \left(w \cdot x_{i}\right)\right]\right.\end{aligned}$

对 $L(w)$ 最大化求解，得到w的估计值。

这块就可以用参数求解的方法了，就不再写了。

利用sklearn包，做回归分析，可以参考刘建平的这篇博客。https://www.cnblogs.com/pinard/p/6035872.html

参考文献

《统计学习方法》-李航

Foneone

发布了56 篇原创文章 · 获赞 29 · 访问量 3万+

私信关注

回归问题-Logistic回归&Logistic回归中为什么是sigmoid函数

Logistic回归

为什么要用sigmoid函数？

Logistic模型参数求解

参考文献

猜你喜欢