Extreme Q-Learning(EQL)极值Q学习(ICLR 2023 top5%)(一)原理概述

为了跟进RL的最新进展和研究，并寻求高质量文章。本节笔者来介绍 ICLR2023 中得分在top前5%的文章《EXTREME Q-LEARNING: MAXENT RL WITHOUT ENTROPY》原理介绍，并进行了学习笔记的归纳总结。方便各位读者进行学习。原文各位读者可以从Openreview中找到，原文链接如下：

同CQL一样，笔者将会从理论与应用两个角度来描述EQL算法，对于想直接应用的读者可以直接跳过理论部分直接查看如何应用。本文的作者最后也给出了EQL和CQL两篇文章之间的联系，希望给各位读者予以启发。本文结构与作者原文结构类似地给出：本篇笔者介绍1，2，3三部分，感兴趣应用的读者请转手阅读第 4 部分。第4部分将会写在《Extreme Q-Learning(EQL)极值Q学习(ICLR 2023 top5%)(二)应用及代码》中，读者可查阅如何应EQL算法和代码。理论或应用根据读者需求进行自行取舍。
本篇内容仅代表读者个人的学习笔记和思路。如有读者产生异议，欢迎各位读者进行批评和指正，笔者希望能够在学习中与各位读者共同进步。

1.预备知识介绍：主要介绍关于带有KL约束的Q-Learning和Fisher-Tippett 极值定理，Gumbel回归简介。

2.极值Q学习方法介绍和基本原理概述，包括：Gumbel回归分析，Gumbel误差分析，Gumbel回归建模以及Gumbel极值Q学习(EQL)与保守Q学习(CQL)之间的联系。

3.极值Q学习算法，实现与动作选取。

4.极值Q学习应用+代码。

1.预备知识介绍

作为开始，首先介绍它的前置算法，这写笔者在另一篇文章中《Conservative Q-Learning(CQL)保守Q学习(二)-CQL2(下界V值估计)》已经进行过简要的介绍了。

1.1 、带有KL约束的 soft-Q-Learning

针对一个时间步长为$T$的MDP过程。RL的目标是想要学习一个策略$\pi (a|s)$，使得下式尽可能的最大。
$$E_{a_t～\pi (a_t|s_t)}[\sum _{t=0}^T{\gamma }^{t}r(s_t,a_t)]$$为了增强这个奖励的影响大小，增添一个参考分布$\mu (a|s)$和KL约束，这又称为最大熵RL,通过简单的化简和整理得到：
$$E_{a_t～\pi (a_t|s_t)}[\sum _{t=0}^T{\gamma }^{t}r(s_t,a_t)]-\beta KL(\pi (a_t|s_t)||\mu (a_t|s_t))$$
$$E_{a_t～\pi (a_t|s_t)}[\sum _{t=0}^T{\gamma }^{t}r(s_t,a_t)-\beta log\frac{\pi (a_t|s_t)}{\mu (a_t|s_t)}]$$这体现在Bellman方程里面上分别对应着以下两种，其实我们已经在《Conservative Q-Learning(CQL)保守Q学习(一)-CQL1(下界Q值估计)》中介绍过了,抽样出一个数据对$(s_t,a_t,s_{t+1})$
$$Q^{k+1}(s_t,a_t)=r(s_t,a_t)+E_{s_{t+1}～T,a_{t+1}～\pi }[Q^k(s_{t+1},a_{t+1})]$$在Q学习的时候，往往我们取可以使得$Q^k(s_t,a_t)$最好的动作，即往往在Q更新时采用这样的 $\pi$:
$$Q^{k+1}(s_t,a_t)=r(s_t,a_t)+E_{s_{t+1}～T}[ma{x}_{a_{t+1}}{Q}^k(s_{t+1},a_{t+1})]$$现在加入了KL约束后，我们发现它的更新变为了：
$$Q^{k+1}(s_t,a_t)=r(s_t,a_t)+E_{s_{t+1}～T,a_{t+1}～\pi }[Q^k(s_{t+1},a_{t+1})-\beta log\frac{\pi (a_{t+1}|s_{t+1})}{\mu (a_{t+1}|s_{t+1})}]$$这样我们发现原来的目标是去max一个$E_{s_{t+1}～T,a_{t+1}～\pi }[Q^k(s_{t+1},a_{t+1})]$。我们求解的时候其实就是寻求一个$\pi$，使得下式最大:
$$argma{x}_{\pi }[\sum T(s_{t+1}|s_t,a_t)\pi (a_{t+1}|s_{t+1})Q(s_{t+1},a_{t+1})]$$很明显这个最大的策略是使得每个状态转移分布下$Q(s_{t+1},a_{t+1})$是最大的。即选一个最大的策略$ma{x}_{a_{t+1}}Q(s_{t+1},a_{t+1})$。
那么同理，我们来推理加入了KL约束后的更新格式，这一部分笔者其实已经在《Conservative Q-Learning(CQL)保守Q学习(二)-CQL2(下界V值估计)》中进行过推导了，采用的是Langrange乘子法求解最大的$\pi$。
$$argma{x}_{\pi }[\sum T(s_{t+1}|s_t,a_t)\pi (a_{t+1}|s_{t+1})[Q(s_{t+1},a_{t+1})-\beta log\frac{\pi (a_{t+1}|s_{t+1})}{\mu (a_{t+1}|s_{t+1})}]$$这里笔者不赘述重新推导了。应用lagrange乘子对$\pi$求导，进行汇总可以求得在每个固定$s_{t+1}$时取最大时候的$\pi$有如下等式成立：
$$\mu (a|s)e^{\frac{Q(s,a)+L-1}{\beta }}=\pi (a|s)$$
$$log(e^{\frac{L-1}{\beta }}\sum \mu (a|s)e^{\frac{Q(s,a)}{\beta }})=log(1)=0\to L=1-\beta log\sum \mu (a|s)e^{\frac{Q(s,a)}{\beta }}$$代入回$L$得到：
$$\pi (a|s)=\frac{\mu (a|s)e^{\frac{Q(s,a)}{\beta }}}{{\sum }_a\mu (a|s)e^{\frac{Q(s,a)}{\beta }}}$$再次代入回原式中有:
$$\sum T(s_{t+1}|s_t,a_t)\pi (a_{t+1}|s_{t+1})\beta log\sum _a\mu (a|s_{t+1})e^{\frac{Q(s_{t+1},a)}{\beta }}$$这也即等同于下式，文中把这个式子称为$V^{\ast }$即：
$$V^{\ast }(s_{t+1})=\beta log\sum _a\mu (a|s_{t+1})e^{\frac{Q(s_{t+1},a)}{\beta }}$$此时加入了KL约束的Q更新规则为：
$$Q^{k+1}(s_t,a_t)=r(s_t,a_t)+E_{s_{t+1}～T}[\beta log\sum _a\mu (a|s_{t+1})e^{\frac{Q(s_{t+1},a)}{\beta }}]$$这个式子称为带有KL约束的soft-Q-Learning更新公式。
若把它写成Bellman算子格式，对应的算子称为软Bellman算子(soft-Bellman operator)$B^{\ast }$，公式为：
$$B^{\ast }Q(s,a)=r(s,a)+E_{s^{\prime }～T}[\beta log\sum _a\mu (a|s^{{}^{\prime }})e^{\frac{Q(s^{{}^{\prime }},a)}{\beta }}]$$其中，称
$$V^{\ast }(s)=\beta log\sum _a\mu (a|s)e^{\frac{Q(s,a)}{\beta }}=L_{\mu }^{\beta }[Q(s,a)]$$并且注意到我们之前得到了最优的策略其实等价于下式:
$$\pi (a|s)=\mu (a|s)e^{\frac{Q(s,a)-V^{\ast }(s)}{\beta }}=\frac{\mu (a|s)e^{\frac{Q(s,a)}{\beta }}}{{\sum }_a\mu (a|s)e^{\frac{Q(s,a)}{\beta }}}$$这即为加入了KL限制的Q-Learning，又称为soft更新Q-learning,笔者这一部分与原文是一致的，不影响读者进行理解，如果不理解原文内容希望笔者这一部分有助于各位去理解，下面是原文中的公式(1)(2)：分别对应笔者上述的推导：

1.2 、 Fisher-Tippett 极值定理与Gumbel-Max Trick

定义:(第一类极值分布)Gumbel distribution(Gumbel分布)$g(\mu ,\beta )$,其概率密度函数满足
$$p(x)=exp[-(\frac{x-\mu }{\beta }+exp[-\frac{x-\mu }{\beta }])]$$(Fisher-Tippett 极值定理):
对于独立同分布的随机变量$X_1,X_2\cdot \cdot \cdot \cdot X_n～f_X$而言：
1、若$f_X$具有指数尾概率分布，则最大值极限分布服从Gumbel分布
$$li{m}_{i\to \infty }ma{x}_i(X_i)～g(\mu ,\beta )$$2、特别地，若$X_1,X_2\cdot \cdot \cdot \cdot X_n～g(\mu ,\beta )$,那么最大值分布服从Gumbel分布
$$ma{x}_i(X_i)～g(\mu ,\beta )$$(Gumbel-Max Trick):
设${ϵ}_1,{ϵ}_2...{ϵ}_n$服从分布$g(0,\beta )$,且它们之间相互独立。现存在一固定集合{ $x_1,x_2,...x_n$},设集合{ $y_1,y_2....y_n$}满足$y_i=x_i+{ϵ}_i$，那么拥有如下结论:
$$ma{x}_i(x_i+{ϵ}_i)～g(\beta log\sum _{i}exp(\frac{x_i}{\beta }),\beta ),argmax(x_i+{ϵ}_i)～softmax(\frac{x_i}{\beta })$$

2、极值Q学习原理概述

2.1、Extreme-Gumbel 误差分析

作为开始，首先作者记录了在传统更新下的Bellman误差$error$,定义如下，作者迭代了RL算法100000次(SAC)为例，每5000次记录一下Bellman误差，记录时选取一个Batch的样本进行计算：
$$Bellman-error=[r(s,a)+Q(s^{\prime },\pi (s^{\prime }))-Q(s,a)]$$$\pi (s^{\prime })$代表着状态$s^{\prime }$在某个已有策略$\pi$下的确定性策略或是一个采样的平均策略。通过误差采样作者发现，Bellman-error更倾向于Gumbel分布，而不是服从正态分布，结果如下图所示。

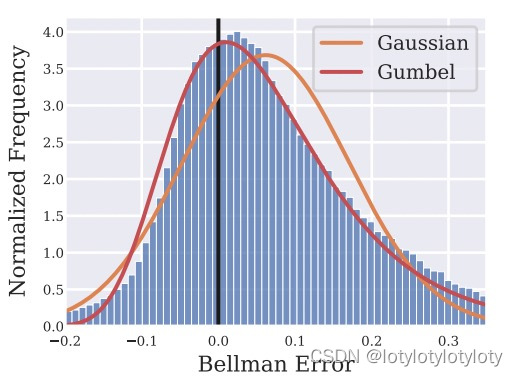
针对此现象的出现，作者给出了简略的描述，但是笔者认为条件和推导是缺乏一定的严谨性的，笔者进行了重新的分析，假设待估计的Q与真实Q函数分别称为:$\hat{Q}$与$\bar{Q}$,并且设$\hat{Q}$是$\bar{Q}$的无偏估计，那么在任意迭代时刻$t$下，都会有:
$${\hat{Q}}_t(s,a)={\bar{Q}}_t(s,a)+{ϵ}_t(s,a)$$根据讨论，在迭代的时候会根据bellman方程计算${\hat{Q}}_{t+1}$，(作者使用了M个估计器中其中一个进行计算)即计算细节为:
$${\hat{Q}}_{t+1}(s,a)=r(s,a)+[ma{x}_{a^{\prime }}{\hat{Q}}_t(s^{\prime },a^{\prime })]=r(s,a)+[ma{x}_{a^{\prime }}[{\bar{Q}}_t(s^{\prime },a^{\prime })+{ϵ}_t(s^{\prime },a^{\prime })]]$$
$${\bar{Q}}_{t+1}(s,a)=E[{\hat{Q}}_{t+1}(s,a)]=r(s,a)+E_{{ϵ}_t}{E}_{s^{\prime }}[ma{x}_{a^{\prime }}[{\bar{Q}}_t(s^{\prime },a^{\prime })+{ϵ}_t(s^{\prime },a^{\prime })]]]$$两式相减会得到:
$${ϵ}_{t+1}(s,a)=[ma{x}_{a^{\prime }}[{\bar{Q}}_t(s^{\prime },a^{\prime })+{ϵ}_t(s^{\prime },a^{\prime })]]-E_{{ϵ}_t}{E}_{s^{\prime }}[ma{x}_{a^{\prime }}[{\bar{Q}}_t(s^{\prime },a^{\prime })+{ϵ}_t(s^{\prime },a^{\prime })]]]$$整理出非随机项，令$t\to \infty$发现:
$$ϵ(s,a)=[ma{x}_{a^{\prime }}[Q(s^{\prime },a^{\prime })+ϵ(s^{\prime },a^{\prime })]]-E_{ϵ}{E}_{s^{\prime }}[ma{x}_{a^{\prime }}[Q(s^{\prime },a^{\prime })+ϵ(s^{\prime },a^{\prime })]]]$$注意到决定$ϵ(s,a)$分布的只有这一随机项$ma{x}_{a^{\prime }}[ϵ(s^{\prime },a^{\prime })]$,并在动作连续的条件下(作者并未提及到这一点，我认为是不对的，不连续没有理由认为下式成立)，根据Fisher-Tippett 极值定理得到误差分布其实近似的服从了Gumbel分布。
$$ϵ(s,a)\propto ma{x}_{a^{\prime }}[ϵ(s^{\prime },a^{\prime })]～Gumbel(\mu ,\beta )$$这启发了我们一个问题，我们在使用神经网络更新网络误差时，在每一个Batch下采用了如下的方案：
$$Loss=\frac{1}{|Batch|}(r(s,a)+Q_{\theta }(s^{\prime },{\pi }_{\delta }(s^{\prime }))-Q_{\theta }(s,a){)}^2$$这默认的是真实分布和预测分布之间的差异为Gauss分布，也对应着极大似然估计，但是现在我们却通过Fisher-Tippett 极值定理说明了误差分布其实是趋近于Gumbel分布而不是Gauss分布，那么该公式就不是很合适了。

2.2、Gumbel 回归分析

现在考虑一组具有Gumbel分布噪声的数据$x_i$，它由下列公式构成，其中${ϵ}_i～-g(0,\beta )$:
$$x_i=(h+{ϵ}_i),{ϵ}_i～-g(0,\beta )$$我们的目标是想去估计出$h$,事实上,$(h-x_i)～g(0,\beta )$:
$$exp[-(\frac{(h-x_i)}{\beta }+exp[-\frac{(h-x_i)}{\beta }])]=exp[(\frac{(x_i-h)}{\beta }-exp[\frac{(x_i-h)}{\beta }])]$$最大化$E_{x_i}log(p(x_i))$即最大化下式:
$$E_{x_i}[[(\frac{(x_i-h)}{\beta }-exp[\frac{(x_i-h)}{\beta }])]]$$在给定参数$\beta$的条件下，下式可被等价为最小化(-1不影响取最大或最小)
$$mi{n}_{h}L(h)=E_{x_i}[[-(\frac{(x_i-h)}{\beta }+exp[\frac{(x_i-h)}{\beta }])]-1]$$这是凸优化问题，存在最小值，对$h$求偏导令为0，可以得到最优的$h$求解为:
$${\nabla }_{h}L(h)=0\to -\frac{1}{\beta }[exp[-\frac{h}{\beta }]E_{x_i}[exp[\frac{x_i}{\beta }]]]=-\frac{1}{\beta }$$两边约去后取log
$$\frac{h}{\beta }=log(E_{x_i}[exp[\frac{x_i}{\beta }]])\to h=\beta log(E_{x_i}[exp[\frac{x_i}{\beta }]])$$这居然神奇的发现一件事情！这个$h$的求解结果和我们在带有KL约束中求解的$V^{\ast }$是一致的，我们来详细观察这两项:
$$V^{\ast }(s)=\beta log\sum _a\mu (a|s)e^{\frac{Q(s,a)}{\beta }}$$
$$h=\beta log(E_{x_i}[exp[\frac{x_i}{\beta }]])=\beta log\sum _{x_i}p(x_i)e^{\frac{x_i}{\beta }}$$这不相当于是，如果我们把x_i视为是Q(s,a)即真实的数据样本，而他又恰好满足Gumbel分布噪声条件(第二部分已经说明了这一点)。而$h$即为我们想要预测的$V^{\ast }$,$p(x_i)$为抽取到该样本的概率大小，若设置为$\mu (a|s)$，这等同于要估计的$V^{\ast }$其实等价于一个Gumbel回归中的系数估计问题！，笔者认为这个思想极为巧妙，不愧是今年top5%的文章。

2.3、Gumbel 回归分析与CQL和SAC的关系

EQL思想看似与CQL毫无关联，其实不然，他们之间有了及其密切的联系，根据2.1节所讨论的。我们已经知道了下面式子中的$ϵ(s,a)$应该服从Gumbel分布，而不是Guass正态分布:
$$\hat{Q}(s,a)=\bar{Q}(s,a)+ϵ(s,a)\to r(s,a)+\gamma E_{s^{\prime }}[ma{x}_{a^{\prime }}\hat{Q}(s^{\prime },a^{\prime })]=\bar{Q}(s,a)+ϵ(s,a)$$若将其看作为:
$$r(s,a)+\gamma E_{s^{\prime },a^{\prime }}[\hat{Q}(s^{\prime },a^{\prime })]=\bar{Q}(s,a)+ϵ(s,a)$$根据2.2所讨论的，我们可以通过Gumbel回归来建模估计$Q(s,a)$,(这里原文作者公式又写错了…)：
$$mi{n}_{Q}L(Q)=E_{s,a～\pi }[-(\frac{(r(s,a)+\gamma E_{s^{\prime },a^{\prime }}[\hat{Q}(s^{\prime },a^{\prime })]-Q(s,a))}{\beta }]+E_{s,a～\mu }[exp[\frac{(r(s,a)+\gamma E_{s^{\prime },a^{\prime }}[\hat{Q}(s^{\prime },a^{\prime })]-Q(s,a))}{\beta }])]-1]$$待估计的$Q$值应该满足:
$${\nabla }_{Q}L(Q)=0\to \frac{\pi (a|s)}{\beta }=\frac{\mu (a|s)}{\beta }exp[\frac{(r(s,a)+\gamma E_{s^{\prime },a^{\prime }}[\hat{Q}(s^{\prime },a^{\prime })]-Q(s,a))}{\beta }])]$$
$$Q(s,a)=r(s,a)+\gamma E_{s^{\prime },a^{\prime }}[\hat{Q}(s^{\prime },a^{\prime })]-\beta log\frac{\pi (a|s)}{\mu (a|s)}$$这即从回归中自然地得到了带有KL损失的Q值更新方式！
若使用软Bellman算子(soft-Bellman operator)$B^{\ast }$，依然的可以得到在下损失函数:
$$mi{n}_{Q}L(Q)=E_{s,a～\mu }[-(\frac{(r(s,a)+\gamma E_{s^{\prime },a^{\prime }}[\hat{Q}(s^{\prime },a^{\prime })]-Q(s,a))}{\beta }]+E_{s,a～\mu }[exp[\frac{(r(s,a)+\gamma E_{s^{\prime },a^{\prime }}[\hat{Q}(s^{\prime },a^{\prime })]-Q(s,a))}{\beta }])]-1]$$进而同理的可以得到这样的Q更新方法:
$$Q^{k+1}(s,a)=B^{\ast }{Q}^k(s,a)$$但是这仍旧需要通过采样的办法来估计$V^{\ast }$，根据我们上面的讨论可以知道
$$B^{\ast }Q(s,a)=r(s,a)+E_{s^{\prime }～T}[\beta log\sum _a\mu (a|s^{{}^{\prime }})e^{\frac{Q(s^{{}^{\prime }},a)}{\beta }}]=r(s,a)+E[V^{\ast }(s^{\prime })]$$我们其实一直知道了，如果使用Gumbel回归直接建立$V^{\ast }$和${\hat{Q}}^k$的联系，便是我们想要的最优值。那么其实$V^{\ast }$可以通过${\hat{Q}}^k$来直接进行Gumbel回归建立。
$$mi{n}_{V^{\ast }}L(V^{\ast })=E_{s,a～\mu }[-(\frac{(r(s,a)+\gamma E_{s^{\prime },a^{\prime }}[\hat{Q}(s^{\prime },a^{\prime })]-Q(s,a))}{\beta }]+E_{s,a～\mu }[exp[\frac{(r(s,a)+\gamma E_{s^{\prime },a^{\prime }}[\hat{Q}(s^{\prime },a^{\prime })]-Q(s,a))}{\beta }])]-1]$$
$$mi{n}_{V^{\ast }}L(V^{\ast })=E_{s,a～\mu }[[-(\frac{(Q^k(s,a)-V(s))}{\beta }+exp[\frac{(Q^k(s,a)-V(s))}{\beta }])]-1]$$求解得到的最优$V^{\ast }(s)=\beta log{\sum }_a\mu (a|s)e^{\frac{Q^k(s,a)}{\beta }}$，这样回避了熵的问题而避免进行采样。

3、极值Q学习算法原理与实现

3.1、策略选择

上述笔者只讲到了如何做$Q$的更新，但是一直没有提出如何做关于策略$\pi$的更新，在这里注意到在1中已经提到过的式子:
$${\pi }^{\ast }(a|s)=\mu (a|s)e^{\frac{Q(s,a)-V^{\ast }(s)}{\beta }}$$那么
$${\pi }^{\ast }(a|s)=argma{x}_{\pi }{E}_{\mu (a|s)}[e^{\frac{Q(s,a)-V^{\ast }(s)}{\beta }}log\pi ]$$即$\pi$取到能够使得概率最大的，即若有某个$\mu (a|s)e^{\frac{Q(s,a)-V^{\ast }(s)}{\beta }}$最大，那么对应的就为那个策略，至于作者为什么采用$log\pi$而不采用$\pi$,我想是为了对齐后续公式，若将$\mu$取成原始的数据分布采样的分布，那么这即为
$${\pi }^{\ast }(a|s)=argma{x}_{\pi }{E}_{{\pi }_{\beta }}[e^{\frac{Q(s,a)-V^{\ast }(s)}{\beta }}log\pi ]$$这将避免在分布外的动作进行选择从而超出分布限制。
如果我们想去抽样分布外的操作(网络的实时分布)而不是从已有动作$\hat{\pi }$中进行采样，那么可以参考和SAC一样的办法来采样动作:($\mu$可以取成当前最新的动作或者上一个动作如${\pi }_k$)
$${\pi }^{\ast }(a|s)=argma{x}_{\pi }{E}_{\hat{\pi }}[Q(s,a)-\beta log(\frac{\pi (a|s)}{\mu (a|s)})]$$

3.2、算法实现

1.初始化网络参数$Q_{\theta },V_{\delta },{\pi }_{\alpha }$和数据集$D$.
2.从数据集$D$中抽取一个Batch出来进行Training(OffLine情况下)或者从Online条件下进行实时收集一个进入到Reply-Buffer中。$(s,a,r,s^{\prime })$
3.执行计算$L(Q)$并更新$Q_{\theta }$
$$L(Q)=E_{s,a,s^{\prime }}[(Q_{\theta }(s,a)-r(s,a)-\gamma V_{\delta }(s^{\prime }){)}^2]$$4.执行计算$L(V)$并更新$V_{\delta }$
$$L(V)=E_{s,a～D}[[-(\frac{(Q_{\theta }(s,a)-V_{\delta }(s))}{\beta }+exp[\frac{(Q_{\theta }(s,a)-V_{\delta }(s))}{\beta }])]-1](Offline)$$
$$L(V)=E_{s,a～{\pi }_{\alpha }}[[-(\frac{(Q_{\theta }(s,a)-V_{\delta }(s))}{\beta }+exp[\frac{(Q_{\theta }(s,a)-V_{\delta }(s))}{\beta }])]-1](Online)$$5.执行计算$L(\pi )$并更新${\pi }_{\alpha }^k$(代表第k次更新)
$$L(\pi )=-E_{s,a～D}[e^{\frac{Q_{\theta }(s,a)-V_{\delta }(s)}{\beta }}log{\pi }_{\alpha }](Offline)$$
$$L(\pi )=-E_{s,a～{\pi }_{\alpha }^k}[Q(s,a)-\beta log(\frac{{\pi }_{\alpha }^k(a|s)}{{\pi }_{\alpha }^{k-1}(a|s)})]$$6.重复2~5直到网络收敛为止