线性回归和局部加权线性回归
由于看完《机器学习实战》第八章中的局部加权线性回归后,敲完代码之后只是知道它是这样的,但不是很清楚内在的原因。书中并没有对其做过多解释,百度也找不到一篇很好的文章来解释 线性回归和局部加权线性回归 两者之间的区别。索性写一写自己对 线性回归和局部加权线性回归 的看法与感悟。也许还是不那么准确,但一定是清晰易懂的。
首先简单聊一聊我们的线性回归,有兴趣的可以看一看我的另一篇博文——机器学习之线性回归,在这里我就不多赘述直接贴公式了。
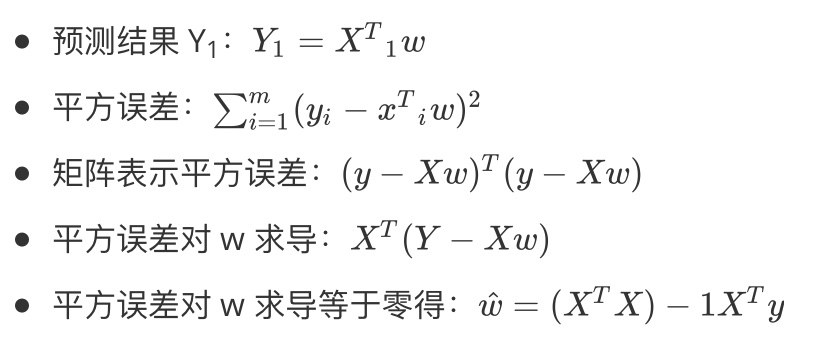

其中的平方误差是我们的在 x=x~i~ 上预测值与实际值的差值平方,而我们需要做的任务就是找到一个最合适的 w 使得该差值平方最小。 再来说说我们的局部加权线性回归(LWLR),它只是在线性回归的基础上加了一个权重,而LWLR通常使用“核”(类似于自持向量机中的核)来对附近的点赋予更高的权重。因此它的公式变成:
$\sum_{i=1}^mW_i(y_i-x^T_iw)^2$
注意:W~i~ 是赋予 x~i~ 权重的矩阵,也可以是向量。
一般我们的 W~i~ 最常用的核是高斯核:$w(i,i)=exp\left({\frac{|x^{(i)}-x|}{-2k^2}}\right)$
 注意:高斯核中的 x 为新预测样本的特征数据即新的 x,它同 w 也是一个向量,参数 k 控制了权值变化的速率。
以上介绍了局部加权线性回归的理论,现在通过图像我们再来形象化的解释局部加权线性回归。首先看看不同 k 下的参数 k 与权重的关系:

- 基于上图我们能发现两个规律:
- 假定我们正预测的点是 x=0.5,一定要记住 x 的对应值不再是一个数值,它的对应值变成了向量,所以这是 x=0.5后的新图像,牢记它变成了一个向量,最上面的是原始数据集;第二个图显示了当 k=0.5 时,大部分数据都用于训练回归模型;最下面的图显示当 k=0.01 时,仅有很少的局部点被用于训练回归模型。
- 如果$|x^{(i)}-x|\approx0$,则$w_{(i)}\approx1$;如果$|x^{(i)}-x|\approx\infty$,则$w^{(i)}\approx0$
重点来了,我刚开始不明白的就是这里,上面 两个注意+图片解释 其实已经揭晓了答案
离 x 很近的样本,权值接近1;而离 x 很远的样本,此时权值接近于0,这样就在 x 局部构成线性回归,x 构成的线性回归依赖的事 x 周边的点,而不类似于线性回归依赖训练集中的所有数据。
 上图红线是某个点 x 基于训练集中所有数据使用线性回归做的结果,黑色直线使用 LWLR 做的结果,由于在每个数据都会重复局部加权的过程,并且不断地每个点的回归系数也在不断的改变,因此它会很好的拟合数据集,进而消除了线性回归拟合不好的缺点。(有点类似极限或者求导或者微积分的思想,总之就是把一个大的物体切割成一大部分,然后对于每一部分进行计算)。
说到了LWLR的优点,不得不说说它的缺点,上一段讲到了训练集中的每个数据都会重复局部加权的过程,因此他的计算量是庞大的,并且他的回归系数是基于周围的数据计算出来的,因此下次需要预测某个数据的分类时,需要再一次输入所有的数据。即线性回归算法是参数学习算法,一旦拟合出合适的回归系数,对于之后的预测,不需要再使用原始训练数据集;局部加权线性回归算法是非参数学习算法,每次进行预测都需要全部的训练数据,无法算出固定的回归系数。
最后看一看 线性回归和不同 k 值的局部加权线性回归 对相同数据集的结果。
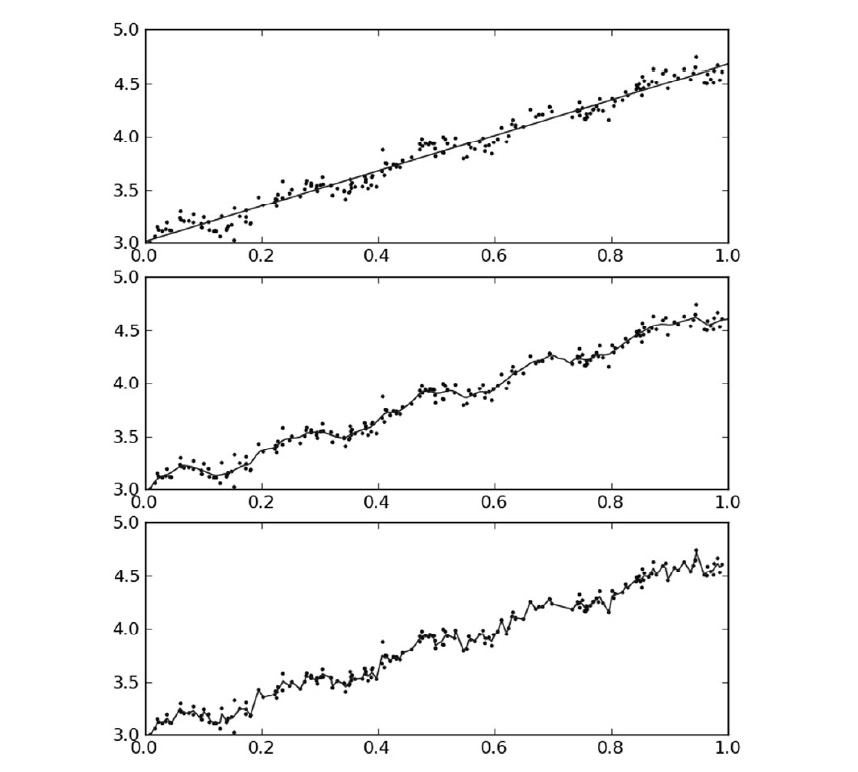
上图第一张图使用的是 k=1 的LWLR(类似于线性回归),第二张图使用的是 k=0.01 的LWLR,第三张图使用的 k=0.003 的 LWLR。第一张图明显欠拟合,第二张图很合适,第三张图过拟合。
==尊重原创==
==可以伸出你的小手点个关注,谢谢!==
博客园地址:https://www.cnblogs.com/chenyoude/
github 地址:https://github.com/nickcyd/machine_learning
微信:a1171958281