角点

一般来说，角点就是极值点，在某些属性上强度最大或者最小的孤立点、线段的终点或拐点等。其实理解角点可以按照我们的直觉来理解，以下图为例，图中用颜色标注的地方都是角点：

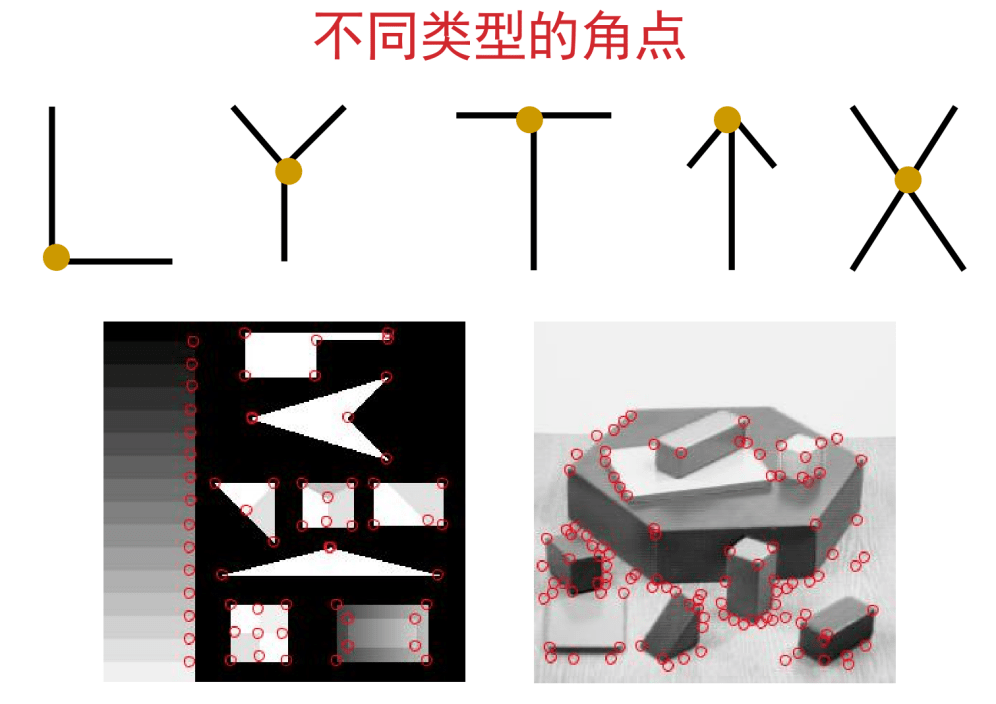
原图地址：理解经典角点检测算法–Harris角点 | 码农家园

对于人类来说，判断角点是很容易的，对于计算机来说又是如何检测到角点的呢？

角点的特征

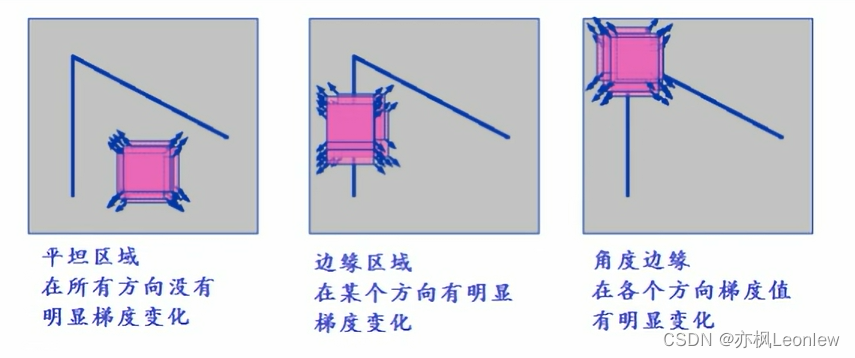
这幅图应该是所有讲角点特征的时候必用的图了。对于平坦区域，当我们对某个子窗口超各个方向进行移动统计区域内梯度变化的时候，基本不会有明显的梯度变化；对于边来说，在某个方向上梯度有明显变化；对于角来说，移动时各个方向的梯度变化都很明显。

上图的意思，就是说我们设定一块小区域或小窗口，然后朝着各个方向进行移动，计算出各个方向移动的时候对应的梯度变化，然后进行对所有方向的变化进行加和。用数学公式表达如下：

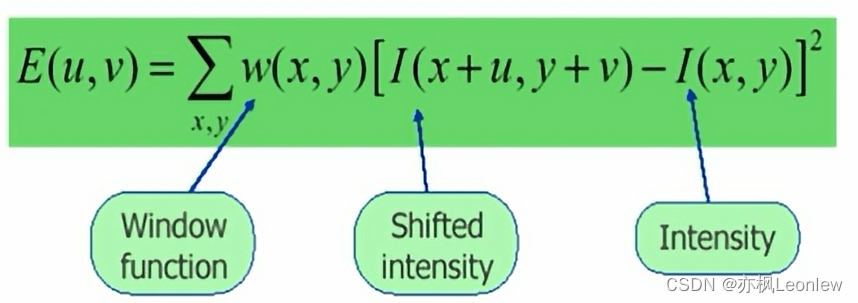
其中：

(x,y)表示窗口w对应的像素坐标位置，有多少个像素点位置取决于窗口的大小

I(x,y)是像素坐标为(x,y)的像素点的灰度值

I(x + u, y + v)是像素坐标为(x + u,y + v)的像素点的灰度值

w(x,y)是一个窗口函数，实际理解为一个权重值就可以了，窗口函数一般有两种思路：

一种是用边界判断的方法，窗口内的像素权重都取1，窗口外的像素权重都取0.实际上这种方式就相当于没有窗口函数了（Moravec）。

另一种思路是用高斯函数做加权，如果窗口W中心点是角点时，移动前与移动后，该点在灰度变化贡献最大；而离窗口w中心(角点)较远的点对灰度变化贡献较小，因此使用二维高斯函数来表示窗口函数是自然而然的事情。

实际上，上面的式子就是Moravec角点检测算法的核心，这种角点检测方法的(u,v)考虑了0°，45°，90°，135°方向的像素点坐标，实际可以理解为(u,v)取值有四种 (1, 0) , (1,1), (0,1)以及(-1,1)。当然，实际应用中，我们也可以让(u,v)取8个方向的值。

从Moravec角点检测算法看，它主要有几个缺点：

1. 不具有旋转不变性和尺度不变性

2. 算法使用方形窗口，因此的E的响应比较容易受到干扰

3. 对边缘响应过于灵敏

二元函数泰勒展开

要理解Harris角点检测，我们需要知道二元函数泰勒展开式。

这个公式看起来很复杂，实际上对于理解Harris角点检测来说，我们不用关注二阶导以上的部分。关注一下一阶导部分即可，我们将h和k换成前一小节的u和v，则有如下近似:

其中， $f_x(x,y)$ 和 $f_x(x,y)$ 分别表示x的一阶偏导和y的一阶偏导。

Harris角点检测

Harris角点检测的w窗口函数一般情况选取的是二维高斯函数，当然也可以用其他窗口函数。

我们先切回到求E的这个等式：

我们对中括号里的 $I(x+u,y+v)$ 这一项，进行二元函数泰勒的一阶展开，可得：

$I(x+u,y+v) \approx I(x,y) + uI_x(x,y) + vI_y(x,y)$

将这个式子带回到原始，可得(这里忽略掉窗口函数)：

然后，将这个完全平方展开的式子改写成矩阵形式：

这个矩阵形式，可以用矩阵乘法计算一下，和之前的式子是相等的。对于求和符号来说，由于u，v和x，y是无关的，我们可以将包含u和v的向量提取出来，得到：

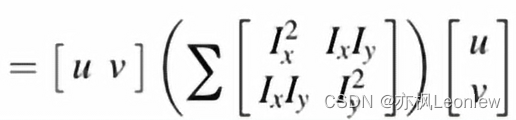
我们将窗口函数放回来，用一个矩阵M来表示，可以得到：

最后，我们可以得到E(u,v)和M的相关函数：

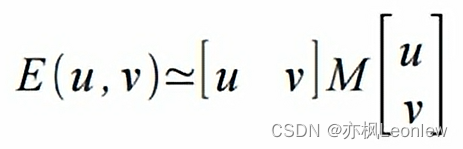
得到这个式子后，我们可以看到，E的值和M是相关的。

我们再来看M矩阵：

这是一个实对称矩阵（2阶方阵，元素都是实数，并且转置矩阵和M本身相等），这里不管每一个Ix和Iy取值如何，相加后矩阵仍然是对称的。

实对称矩阵一定可以做相似对角化，即存在正交矩阵P，使得

$P^{-1}MP = \begin{bmatrix} \lambda _1 & 0& \\ 0 & \lambda_2 \end{bmatrix}$

$\lambda_1$ ， $\lambda_2$ 是M的特征值，由上面的式子可以得：

$M = P\begin{bmatrix} \lambda _1 & 0& \\ 0 & \lambda_2 \end{bmatrix}P^{-1}$

由于P是正交矩阵，P的转置 $P^T = P^{-1}$ ，因此，有：

$M = P\begin{bmatrix} \lambda _1 & 0& \\ 0 & \lambda_2 \end{bmatrix}P^T$

将M代回到E(u,v),可以得到：

$E(u,v) \approx [u,v]P\begin{bmatrix} \lambda _1 & 0& \\ 0 & \lambda_2 \end{bmatrix}P^T\begin{bmatrix} u\\ v \end{bmatrix} = [u,v]P\begin{bmatrix} \lambda _1 & 0& \\ 0 & \lambda_2 \end{bmatrix}P^T[u,v]^T$

根据矩阵的转置运算规则： $(AB)^T = B^TA^T$ ,可以知道：

$P^T[u,v]^T = ([u,v]P)^T$

假设[u,v]P的结果是[u',v'],则有：

$E(u,v) \approx [u',v']\begin{bmatrix} \lambda _1 & 0& \\ 0 & \lambda_2 \end{bmatrix}\begin{bmatrix} u'\\ v' \end{bmatrix}$

将这个式子展开，有：

$E(u,v) \approx (u')^2\lambda_1 + (v')^2\lambda_2 = \frac{u'^2}{\frac{1}{\lambda_1}} + \frac{v'^2}{\frac{1}{\lambda_2}} = \frac{u'^2}{\lambda_1^{-1}} + \frac{v'^2}{\lambda_2^{-1}}$

可以看到，最终得到的式子其实表示的是椭圆的方程。标准椭圆方程为：

$\frac{x^2}{a^2} +\frac{y^2}{b^2} = 1$

可以将前面式子的 $\lambda_1^{-1}$ 和 $\lambda_2^{-1}$ 对应于 $a^2$ 和 $b^2$ ,因此这个椭圆的两个轴的长度分别对应于 $\lambda_1^{-\frac{1}{2}}$ 和 $\lambda_2^{-\frac{1}{2}}$ 。这两个数就是harris角点检测的文章中常常会看到的椭圆的两个轴的参数：

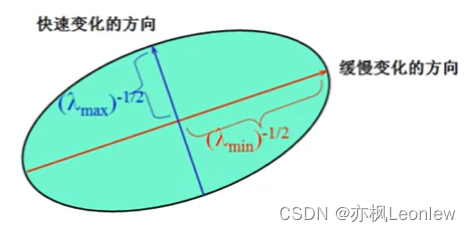
结合角点检测原理和推导出椭圆方程来看，如果是角点，则E(u,v)的值要大，对应 $\lambda_1$ 和 $\lambda_2$ 也必须同时都大才能满足。因此我们就知道了下面这幅图的含义：

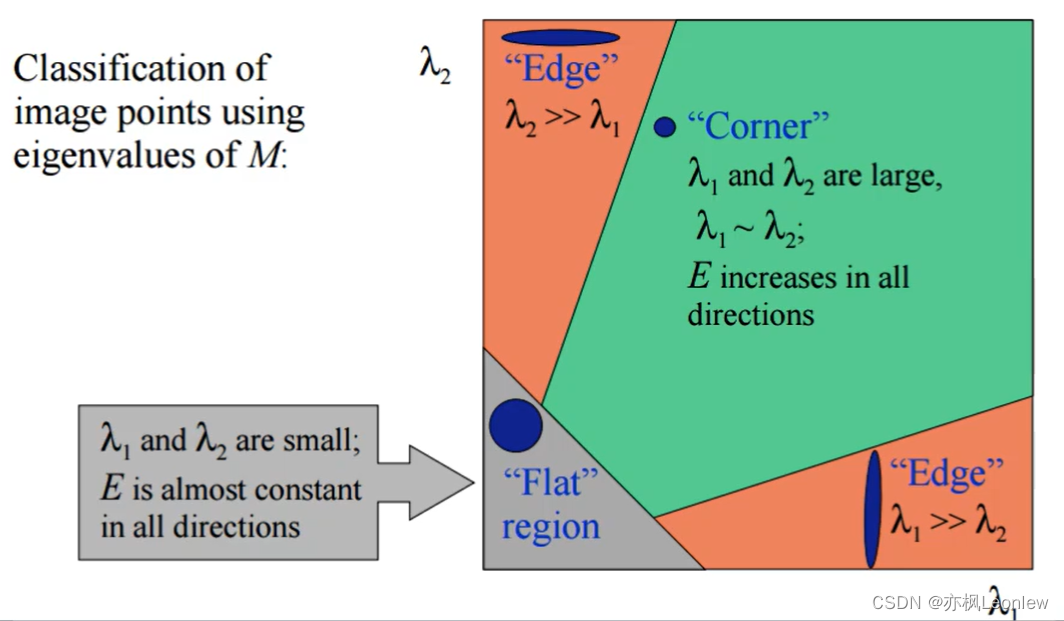
对于平坦区域：E(u,v)值非常小，对应 $\lambda_1$ 和 $\lambda_2$ 也会很小。

对于边缘：E(u,v)值比平坦区域大，但没有角点的E(u,v)值大，此时要么 $\lambda_1$ 比 $\lambda_2$ 大很多，要么反过来。

对于角点：E(u,v)值很大， $\lambda_1$ 和 $\lambda_2$ 都比较大，并且两者接近。

响应函数R

前面我们基本知道了Harris角点检测的基本原理和推导过程，如果直接使用前面的结论来做检测，理论上是可以的。但是会有一件麻烦事，就是求M矩阵的特征值 $\lambda_1$ 和 $\lambda_2$ 。有没有比较好的办法不用求它们的值，通过矩阵的一些性质就能估算出 $\lambda_1$ 和 $\lambda_2$ 的关系呢？答案是有，发明算法的两位大神想到了对称矩阵的行列式detM以及矩阵的迹和 $\lambda_1$ 、 $\lambda_2$ 之间的关系：

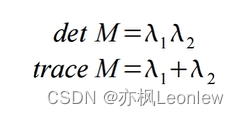
对矩阵M求行列式值和矩阵的迹的运算显然比计算出特征值要来得简单高效。那么最终每个像素的像素点响应R被定义为：

当k取的数值比较合适的时候，这个R响应函数就能较好的反映出 $\lambda_1$ 和 $\lambda_2$ 之间的关系。

k是一个经验值，取值一般在（0.04-0.06）。k值越大，会降低角点检测的灵敏度，减少检测角点的数量；减少k值，会增加角点检测的灵敏度，增加检测角点的数量。

对于是否是焦点的判断，最终就是判断R的值：

角点——R为大数值正数
边缘——为大数值负数
平坦区——为小数值

Harris角点检测具有旋转不变性，但不具有尺度不变性。

Harris角点检测的稳定性和 k 值有关，而 k 是个经验值，不好设定最佳值。

Shi-Tomasi 角点检测

Shi-Tomasi 角点检测改进了Harris角点检测算法的R响应函数，R响应函数更加简单高效。

Shi-Tomasi 发现角点的稳定性其实和矩阵 M 的较小特征值有关，于是直接用较小的那个特征值作为分数。这样就不用调整k值了。如果矩阵M的两个特征值中较小的那一个大于设定的阈值，那么这个点是角点；如果两个特征值都小于阈值，那较小的特征值也必定小于阈值，那这个点就是平坦区域的点；如果其中一个特征值大于阈值而另外一个特征值小于阈值，那么这个点就是边缘点。所以我们只需要判断矩阵M的两个特征值中较小的那一个特征值是否是大于阈值，如果大于阈值这个点就是强角点。

关于相关线性代数知识比如实对称矩阵的正交对角化和矩阵的行列式、特征值和迹相关内容，可以参考这里：

线性代数学习笔记——第七十四讲——实对称矩阵的相似对角化_实对称矩阵相似对角化_预见未来to50的博客-CSDN博客1. 对任一实对称矩阵，存在正交矩阵，满足矩阵的连乘等于对角矩阵2. 求正交矩阵与对角矩阵的计算步骤3. 实对称矩阵的正交矩阵与对角矩阵的求解示例4. 两个实对称矩阵相似的充要条件是它们有相同的特征值..._实对称矩阵相似对角化https://blog.csdn.net/hpdlzu80100/article/details/100715880

31.《线性代数》实对称矩阵的正交对角化_哔哩哔哩_bilibili-, 视频播放量 7820、弹幕量 31、点赞数 207、投硬币枚数 112、收藏人数 114、转发人数 35, 视频作者 mathfish2020, 作者简介厦门大学余铌娜，相关视频：26.《线性代数》正交矩阵，《线性代数》-厦门大学-余铌娜，8.《线性代数》分块矩阵的行列式，25.《线性代数》规范正交基——施密特(Schmidt)正交化方法，13.《线性代数》用初等变换求逆矩阵及例子，19.《线性代数》向量组的最大无关组与秩-1，36.《线性代数》正定二次型与正定矩阵-1，12.《线性代数》矩阵的初等变换及初等矩阵，38.《线性代数》习题课：二次型、正定矩阵，大学生期末仅剩1小时考线性代数怎么搞https://www.bilibili.com/video/BV1G54y1R76C/?spm_id_from=333.337.search-card.all.click&vd_source=474bff49614e62744eb84e9f8340d91a 线性代数——韦达定理、矩阵行列式、矩阵的迹、矩阵特征值及关系_矩阵的迹和特征值关系_xia ge tou lia的博客-CSDN博客一、韦达定理回顾对于一元二次方程（且），设两个根为，。则：且易得到：，以上定理交代了两根之和（积）与方程系数的关系。依次类推：对于一元三次方程，设三个根为，，。易得到：，故对于一元次的方程，我们可以表示为，其中代表第次项的系数，代表常数项。则，二、矩阵的特征值及特征向量回顾以下知识点来自吴传生主编的《线性代数》【知识点1】：设是阶方阵，如果标量和..._矩阵的迹和特征值关系https://blog.csdn.net/huangguohui_123/article/details/105940318 在实对称相似对角化中，如何快速反求矩阵A ？_哔哩哔哩_bilibili不求特征向量，不求逆，减少计算量！, 视频播放量 7367、弹幕量 19、点赞数 142、投硬币枚数 81、收藏人数 149、转发人数 37, 视频作者 KireiIU, 作者简介 Папа агрессивен, а сын ускоряется，相关视频：【俗说矩阵】实对称矩阵和相似对角化究竟有什么关系呢？看了就知道！，对称矩阵相似对角化，怎样将矩阵对角化？，矩阵【相似对角化】的本质+条件，5.1实对称矩阵，反求矩阵的两种方法，实对称矩阵为什么一定可以相似对角化|【线代基础】，已知基础解系反求矩阵A，小可爱们都要会哦。，实对称矩阵的相似对角化及独特性质，正交矩阵及其5条重要性质汇总，以及斯密特正交化，矩阵可对角化条件及实对称矩阵对角化的方法https://www.bilibili.com/video/av718563485/?vd_source=474bff49614e62744eb84e9f8340d91a参考资料：

角点检测harris corner公式推导详解_harris角点推导_WorstCoder的博客-CSDN博客
 Harris角点检测原理推导过程_ha_lee的博客-CSDN博客

计算机视觉——harris角点检测之harris角点响应函数R_-wshuhu-的博客-CSDN博客

Harris和Shi-tomasi角点检测笔记（详细推导）

角点

角点的特征

二元函数泰勒展开

Harris角点检测

响应函数R

Shi-Tomasi 角点检测

猜你喜欢