算法设计 - KMP算法

字符串模式匹配问题

假设有两个字符串S，T，其中S是主串（正文串），T为子串（模式串），

我们需要在S中查找与T相匹配的子串，如果成功找到，则返回匹配的子串第一个字符在主串中的位置。

暴力算法解决

图示

假设S = "aabaabaaf"，T = "aabaaf"，则暴力解法过程如下图所示：

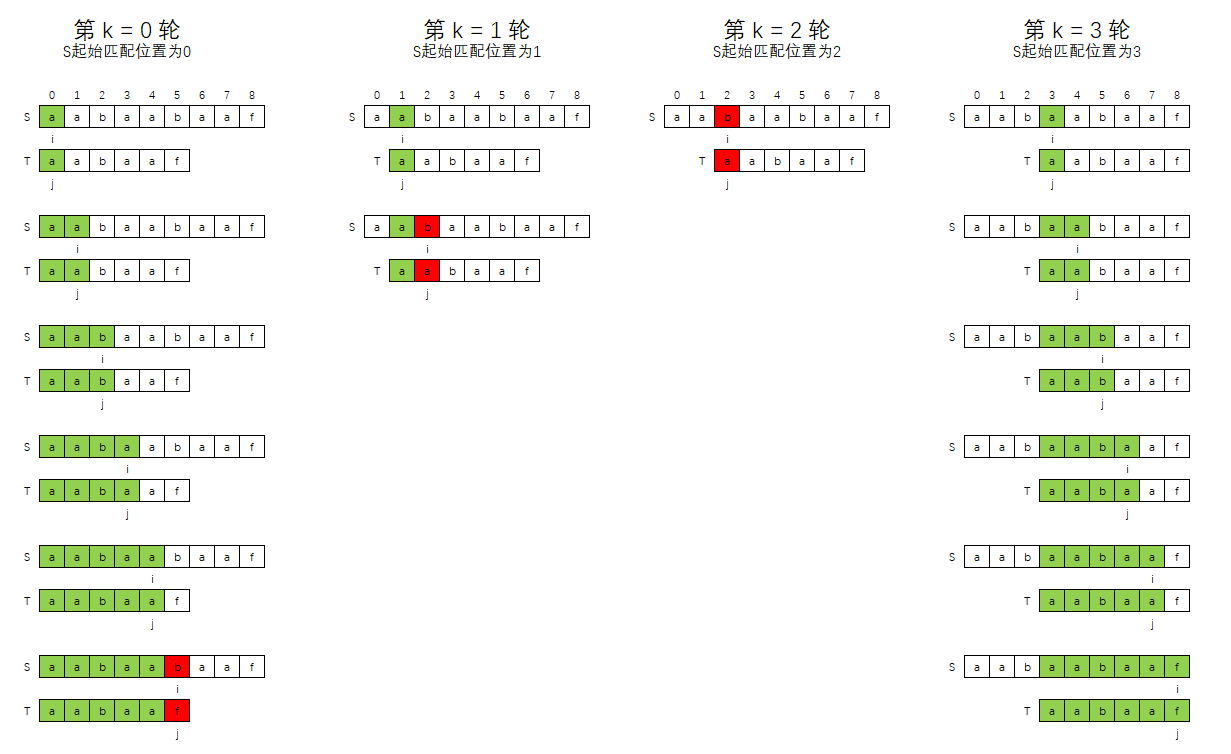
 上图匹配过程中，分为两个循环：

外层循环，即匹配的轮数控制，或者说是，S串的匹配起始位置控制，比如：

• 第0轮，T串是从S串的0索引位置开始匹配
• 第1轮，T串是从S串的1索引位置开始匹配
• ...
• 第k轮，T串是从S串的 k 索引位置开始匹配

内层循环，即T串和S串的 k ~ k + t.length 范围进行逐个字符一一匹配，

• 如果发现存在对应位的字符不一致，则说明当前轮匹配失败，直接进入下一轮
• 如果所有位置上的字符都相同，则说明匹配成功，即在S中找到了和T相同的子串，且该子串起始位置是k

假设，s.length = n，t.length = m，则暴力解法的时间复杂度为O(n * m)

代码实现

JS算法源码

/**
 * @param {*} s 正文串
 * @param {*} t 模式串
 * @returns 在s中查找与t相匹配的子串，如果成功找到，则返回匹配的子串第一个字符在主串中的位置
 */
function indexOf(s, t) {
  // k指向s的起始匹配位置
  for (let k = 0; k <= s.length - t.length; k++) {
    let i = k;
    let j = 0;

    while (j < t.length && s[i] == t[j]) {
      i++;
      j++;
    }

    if (j == t.length) {
      return k;
    }
  }

  return -1;
}

const s = "aabaabaafaab";
const t = "aabaaf";
console.log(indexOf(s, t));

Java算法源码

public class Main {
  public static void main(String[] args) {
    String s = "aabaabaaf";
    String t = "aabaaf";
    System.out.println(indexOf(s, t));
  }

  /**
   * @param s 正文串
   * @param t 模式串
   * @return 在s中查找与t相匹配的子串，如果成功找到，则返回匹配的子串第一个字符在主串中的位置
   */
  public static int indexOf(String s, String t) {
    // k指向s的起始匹配位置
    for (int k = 0; k <= s.length() - t.length(); k++) {
      int i = k;
      int j = 0;

      while (j < t.length() && s.charAt(i) == t.charAt(j)) {
        i++;
        j++;
      }

      if (j == t.length()) {
        return k;
      }
    }

    return -1;
  }
}

Python算法源码

def indexOf(s, t):
    """
    :param s: 正文串
    :param t: 模式串
    :return: 在s中查找与t相匹配的子串，如果成功找到，则返回匹配的子串第一个字符在主串中的位置
    """

    # k指向s的起始匹配位置
    for k in range(len(s) - len(t) + 1):
        i = k
        j = 0

        while j < len(t) and s[i] == t[j]:
            i += 1
            j += 1

        if j == len(t):
            return k

    return -1


if __name__ == '__main__':
    s = "aabaabaaf"
    t = "aabaaf"

    print(indexOf(s, t))

KMP算法

暴力解法的改进策略

对于字符串模式匹配问题，暴力算法并非最优解决方案，虽然s，t都是随机串，但是这些随机串也会存在一定规律可以利用。

比如前面例子中，s = "aabaabaaf"，t = "aabaaf"

在第0轮匹配失败后，第1轮，第2轮是否注定失败了呢？

如下图是第0轮最后一次匹配失败的情况：

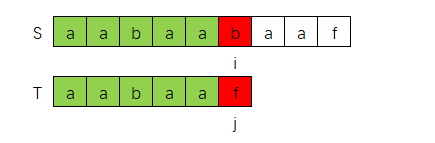
我们观察其中匹配成功的部分，即"aabaa"部分，这部分具有一定的对称性，

如果我们将S,T的"aabaa"后面部分抽象化，如下图所示，那么：

• 第0轮匹配失败是因为“抽象部分”的匹配失败
• 第1轮，第2轮匹配失败，其实就是"aabaa"部分的匹配失败：

 我们将第1轮，第2轮，第3轮再次简化一下，如下图所示：

那么是不是很显然可以发现，第1轮，第2轮是注定失败的。

我们再举一个例子：

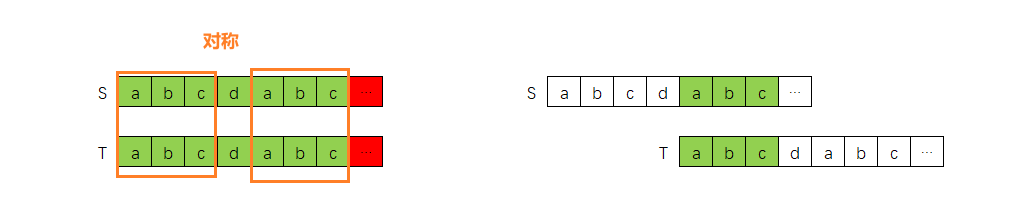
如果上面S,T在第0轮因为抽象部分匹配失败，那么下一轮，其实可以直接跳转到对称位置开始进行匹配，因为非对称位置的匹配肯定是失败的。

这样的话，是不是跳过了两轮匹配，即节省了两轮匹配的时间。

请大家再思考一下，上面直接跳转的对称部分重新匹配真的是只节省两轮匹配的过程吗？

下面图示是，第0轮匹配失败后，直接跳到对称部分开始重新匹配

如果对应到暴力解法过程的话，那么下面画X的部分就都是跳过的过程

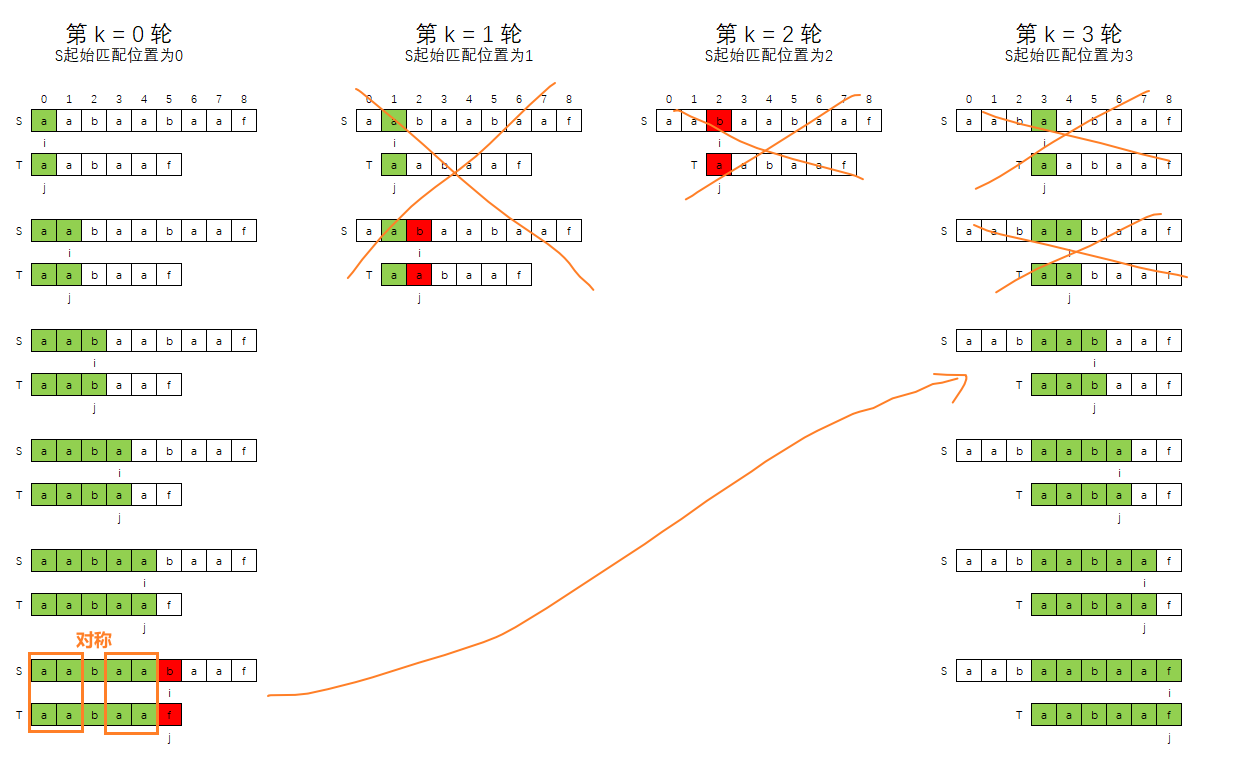
我们再观察下这个跳到对称部分的过程中，i，j指针的变化

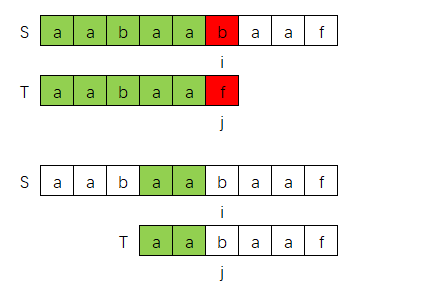
可以发现，i 指针在S中的位置并没有改变，而 j 指针回退指向到了T的"aabaa"对称字符串的中心位置"b"。

那么上面这个改进算法的时间复杂度是多少呢？

由于上面算法中，保证了 i 指针不会回退，因此时间复杂度只有O(n)。

而这个算法其实就是KMP算法。

前缀表

前面我们已经知道了KMP算法的大致原理，其中最关键的就是在模式串T中找其子串的对称部分，

那么该如何通过代码来实现这个功能呢？

KMP算法的三个创始人K，M，P提出了前缀表的概念。

比如T = "aabaaf"，则我们首先需要找到T的所有子串：

• a
• aa
• aab
• aaba
• aabaa
• aabaaf

然后计算这些子串的最长相同的前缀和后缀的长度

假设字符串s长度为n，那么：

• 前缀就是起始索引必须为0，结束索引＜n-1的所有子串
• 后缀就是结束索引必须为n-1，起始索引必须>0的所有子串

因此

• 前缀和后缀不能是字符串s本身
• 字符串s的前缀和后缀是可能存在重叠部分的

我们举一个例子，比如列出T的子串"aabaa"的所有的前缀和后缀

长度	前缀	后缀
1	a	a
2	aa	aa
3	aab	baa
4	aaba	abaa

其中最长且相同的前后缀是"aa"。

注意，判断前缀和后缀是否相同，都是从左往右逐一比对，因此上面例子中，长度为3的前缀"aab"和后缀"baa"是不相同的。

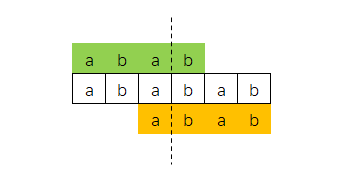
还有相同的前缀、后缀是可能存在重叠，

比如下面字符串"ababab"，最长相同的前缀和后缀是"abab"

长度	前缀	后缀
1	a	b
2	ab	ab
3	aba	bab
4	abab	abab
5	ababa	babab

因此T = "aabaaf"所有子串的最长相同的前缀和后缀的长度分别为：

T的子串	最长相同的前后缀	最长相同的前后缀的长度
a	无	0
aa	a	1
aab	无	0
aaba	a	1
aabaa	aa	2
aabaaf	无	0

上面前缀表，我们一般用next数组表示

next = [0, 1, 0, 1, 2, 0]

前缀表的应用

前面我们手算出了前缀表next数组

next = [0, 1, 0, 1, 2, 0]

那么next数组元素的含义是什么呢？

next[j]元素其实就是0~j子串的最长相同前后缀长度，比如：

• next[0]，就是T的0~0子串"a"的最长相同前后缀长度
• next[1]，就是T的0~1子串"aa"的最长相同前后缀长度
• next[2]，就是T的0~2子串"aab"的最长相同前后缀长度
• next[3]，就是T的0~3子串"aaba"的最长相同前后缀长度
• next[4]，就是T的0~4子串"aabaa"的最长相同前后缀长度
• next[5]，就是T的0~5子串"aabaaf"的最长相同前后缀长度

那么如何将next应用到KMP算法中呢？

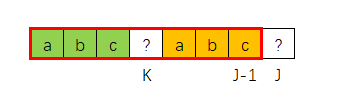
比如下图中，s[i] != t[j]时，我们前面分析过，需要做如下动作：

• i 指针保持指向不变
• j 指针回退到对称部分的中心位置

这样运动的好处是，

• 避免了 i 指针的回退（增加冗余比较轮次）
• 避免了 对称部分中心位置之前部分的冗余匹配（因为必然相同，所以是冗余匹配）

但是，这里的对称部分中心位置的表述，其实非常不研究，更严谨一点的表述：应该是最长相同前后缀中“前缀的结束位置的后一个位置”。

而最长相同前后缀的前缀结束位置的后一个位置，其实就是最长相同前后缀的长度。

因此，当s[i] != t[j] 时，我们应该让 j = next[ j - 1 ]

另外，如果 j = 0 时就匹配不上，此时next[j-1]就发生越界异常，因此针对这种i情况，我们应该特殊处理，如下图所示，就是一个 j = 0无法匹配的情况：

此时，我们应该让 i++，j 保持不变，继续匹配

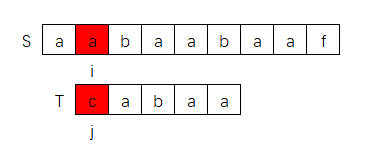
这其实和前面KMP算法规定的 i 指针不回退这一条件不冲突。因为上面过程 i 指针没有发生回退。

KMP算法实现（不包含前缀表生成实现）

这里关于前缀表的生成逻辑先不实现，单纯实现KMP算法的逻辑

JS算法源码

/**
 * @param {*} s 正文串
 * @param {*} t 模式串
 * @returns 在s中查找与t相匹配的子串，如果成功找到，则返回匹配的子串第一个字符在主串中的位置
 */
function indexOf(s, t) {
  // 手算的T串"aabaaf"对应的前缀表
  let next = [0, 1, 0, 1, 2, 0];
  // 手算的T串"cabaa"对应的前缀表
  // next = [0, 0, 0, 0, 0];

  let i = 0; // 扫描S串的指针
  let j = 0; // 扫描T串的指针

  // 如果 i 指针扫描到S串结束位置，或者 j 指针扫描到T串的结束位置，都应该结束查找
  while (i < s.length && j < t.length) {
    if (s[i] == t[j]) {
      // 如果 s[i] == t[j]，则当前位置匹配成功，继续匹配下一个位置
      i++;
      j++;
    } else {
      // 如果 s[i] != t[j]，则说明当前位置匹配失败，
      // 根据KMP算法，我们只需要回退T串的 j 指针到 next[j-1]位置,即最长相同前缀的结束位置后面一个位置，而S串的 i 指针保持不动
      if (j > 0) {
        j = next[j - 1];
      } else {
        // 如果 j = 0,则说明S子串subS和T在第一个字符上就匹配不上, 此时T不匹配字符T[j]前面已经没有前后缀了，因此只能匹配下一个S子串
        i++;
      }
    }
  }

  // 如果最终可以在S串中找到匹配T的子串，则T串的所有字符都应该被j扫描过，即最终 j = t.length
  if (j >= t.length) {
    // 则S串中匹配T的子串的首字符位置应该在 i - t.length位置，因为 i 指针最终会扫描到S串中匹配T的子串的结束位置的后一个位置
    return i - j;
  } else {
    // 否则就是没有在S中找到匹配T的子串
    return -1;
  }
}

const s = "aabaabaafaab";
let t = "aabaaf";
// t = "cabaa"; // 该T串用于测试第一个字符就不匹配的情况
console.log(indexOf(s, t));

Java算法源码

public class Main {
  public static void main(String[] args) {
    String s = "aabaabaaf";
    String t = "aabaaf";
    //    t = "cabaa"; // 该T串用于测试第一个字符就不匹配的情况

    System.out.println(indexOf(s, t));
  }

  /**
   * @param s 正文串
   * @param t 模式串
   * @return 在s中查找与t相匹配的子串，如果成功找到，则返回匹配的子串第一个字符在主串中的位置
   */
  public static int indexOf(String s, String t) {
    // 手算的T串"aabaaf"对应的前缀表
    int[] next = {0, 1, 0, 1, 2, 0};
    // 手算的T串"cabaa"对应的前缀表
    //    next = new int[] {0, 0, 0, 0, 0};

    int i = 0; // 扫描S串的指针
    int j = 0; // 扫描T串的指针

    // 如果 i 指针扫描到S串结束位置，或者 j 指针扫描到T串的结束位置，都应该结束查找
    while (i < s.length() && j < t.length()) {
      // 如果 s[i] == t[j]，则当前位置匹配成功，继续匹配下一个位置
      if (s.charAt(i) == t.charAt(j)) {
        i++;
        j++;
      } else {
        // 如果 s[i] != t[j]，则说明当前位置匹配失败，
        // 根据KMP算法，我们只需要回退T串的 j 指针到 next[j-1]位置,即最长相同前缀的结束位置后面一个位置，而S串的 i 指针保持不动
        if (j > 0) {
          j = next[j - 1];
        } else {
          // 如果 j = 0,则说明S子串subS和T在第一个字符上就匹配不上, 此时T不匹配字符T[j]前面已经没有前后缀了，因此只能匹配下一个S子串
          i++;
        }
      }
    }

    // 如果最终可以在S串中找到匹配T的子串，则T串的所有字符都应该被j扫描过，即最终 j = t.length
    if (j == t.length()) {
      // 则S串中匹配T的子串的首字符位置应该在 i - t.length位置，因为 i 指针最终会扫描到S串中匹配T的子串的结束位置的后一个位置
      return i - j;
    } else {
      // 否则就是没有在S中找到匹配T的子串
      return -1;
    }
  }
}

Python算法源码

def indexOf(s, t):
    """
    :param s: 正文串
    :param t: 模式串
    :return: 在s中查找与t相匹配的子串，如果成功找到，则返回匹配的子串第一个字符在主串中的位置
    """

    # 手算的T串"aabaaf"对应的前缀表
    next = [0, 1, 0, 1, 2, 0]

    # 手算的T串"cabaa"对应的前缀表
    # next = [0, 0, 0, 0, 0]

    i = 0  # 扫描S串的指针
    j = 0  # 扫描T串的指针

    # 如果 i 指针扫描到S串结束位置，或者 j 指针扫描到T串的结束位置，都应该结束查找
    while i < len(s) and j < len(t):
        # 如果 s[i] == t[j]，则当前位置匹配成功，继续匹配下一个位置
        if s[i] == t[j]:
            i += 1
            j += 1
        else:
            # 如果 s[i] != t[j]，则说明当前位置匹配失败
            # 根据KMP算法，我们只需要回退T串的 j 指针到 next[j-1]位置,即最长相同前缀的结束位置后面一个位置，而S串的 i 指针保持不动
            if j > 0:
                j = next[j - 1]
            else:
                # 如果 j = 0,则说明S子串subS和T在第一个字符上就匹配不上, 此时T不匹配字符T[j]前面已经没有前后缀了，因此只能匹配下一个S子串
                i += 1

    # 如果最终可以在S串中找到匹配T的子串，则T串的所有字符都应该被j扫描过，即最终 j = t.length
    if j >= len(t):
        # 则S串中匹配T的子串的首字符位置应该在 i - t.length位置，因为 i 指针最终会扫描到S串中匹配T的子串的结束位置的后一个位置
        return i - j
    else:
        # 否则就是没有在S中找到匹配T的子串
        return -1


if __name__ == '__main__':
    s = "aabaabaaf"
    t = "aabaaf"
    # t = "cabaa"  # 该T串用于测试第一个字符就不匹配的情况

    print(indexOf(s, t))

前缀表的生成

前面我们已经手算过了前缀表，但是手算过程是一个暴力枚举的过程，即枚举出所有的前缀、后缀，然后对比相同的长度的前缀、后缀，看对应内容是否也是相同的。

关于前缀表的生成，我们可以利用动态规划求解。

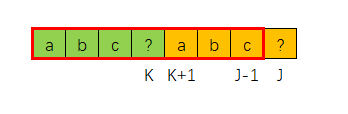
我们现在要求NEXT[J]，假设已知 NEXT[J-1] = K，比如下图

如果T[J] == T[K] 的话，那么 

 

那么 NEXT[J]  = K + 1

（PS：如果不能理解的话，可以将上面？替换成"d"，然后手算一下NEXT[J]）

如果T[J] ! = T[K]的话

那么NEXT[J]该如何求解呢？

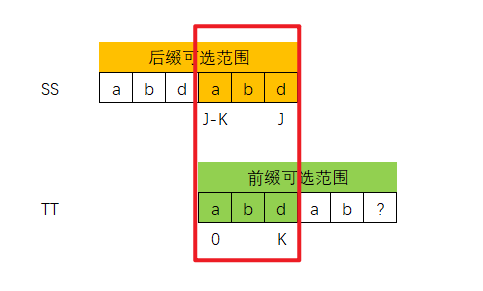
其实换个思维，是可以套用前面KMP算法思路，如下图所示，我们可以将T串想象成两个分身串，如下图所示的SS和TT串，

其中SS串是原T串的后缀范围部分，TT串是是原T串的前缀范围部分

现在已经确定  SS[J] ! = TT[K] ，因此我们应该让TT串的K指针回退，即回退到NEXT[K-1]位置

然后继续比较T[J] 和 T[K]：

• 如果T[J] == T[K]，则NEXT[J] = K + 1

这里为啥可以直接认为0~K-1部分一定和J-K ~ J-1部分相同呢？

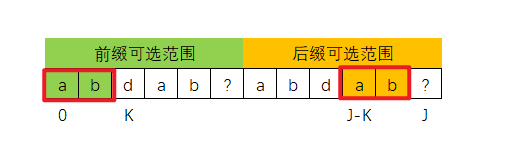
其实上面0~K-1部分、J-K ~ J-1部分回归到T串中的话，如下图所示

 再往前走一步的话，如下图所示

• 如果T[J] ! = T[K]，则再次 K = NEXT[K-1]

因此，这里前缀表的生成逻辑，其实也是套用了KMP算法，只是这里的前缀表只有一个T串，我们需要抽象为两个虚拟串SS（虚拟主串），TT（虚拟模式串）。

关于前缀表的代码实现，请看下面小节代码实现中getNext方法，可以对比KMP算法逻辑来看二者的相似之处。

KMP算法的实现（包含前缀表生成实现）

Java算法源码

public class Main {
  public static void main(String[] args) {
    String s = "xyz";
    String t = "z";

    System.out.println(indexOf(s, t));
  }

  /**
   * @param s 正文串
   * @param t 模式串
   * @return 在s中查找与t相匹配的子串，如果成功找到，则返回匹配的子串第一个字符在主串中的位置
   */
  public static int indexOf(String s, String t) {
    int[] next = getNext(t);

    int i = 0; // 扫描S串的指针
    int j = 0; // 扫描T串的指针

    // 如果 i 指针扫描到S串结束位置，或者 j 指针扫描到T串的结束位置，都应该结束查找
    while (i < s.length() && j < t.length()) {
      // 如果 s[i] == t[j]，则当前位置匹配成功，继续匹配下一个位置
      if (s.charAt(i) == t.charAt(j)) {
        i++;
        j++;
      } else {
        // 如果 s[i] != t[j]，则说明当前位置匹配失败，
        // 根据KMP算法，我们只需要回退T串的 j 指针到 next[j-1]位置,即最长相同前缀的结束位置后面一个位置，而S串的 i 指针保持不动
        if (j > 0) {
          j = next[j - 1];
        } else {
          // 如果 j = 0,则说明S子串subS和T在第一个字符上就匹配不上, 此时T不匹配字符T[j]前面已经没有前后缀了，因此只能匹配下一个S子串
          i++;
        }
      }
    }

    // 如果最终可以在S串中找到匹配T的子串，则T串的所有字符都应该被j扫描过，即最终 j = t.length
    if (j == t.length()) {
      // 则S串中匹配T的子串的首字符位置应该在 i - t.length位置，因为 i 指针最终会扫描到S串中匹配T的子串的结束位置的后一个位置
      return i - j;
    } else {
      // 否则就是没有在S中找到匹配T的子串
      return -1;
    }
  }

  public static int[] getNext(String t) {
    int[] next = new int[t.length()];

    int j = 1;
    int k = 0;

    while (j < t.length()) {
      if (t.charAt(j) == t.charAt(k)) {
        next[j] = k + 1;
        j++;
        k++;
      } else {
        if (k > 0) {
          k = next[k - 1];
        } else {
          j++;
        }
      }
    }

    return next;
  }
}

JS算法源码

/**
 * @param {*} s 正文串
 * @param {*} t 模式串
 * @returns 在s中查找与t相匹配的子串，如果成功找到，则返回匹配的子串第一个字符在主串中的位置
 */
function indexOf(s, t) {
  let next = getNext(t);

  let i = 0; // 扫描S串的指针
  let j = 0; // 扫描T串的指针

  // 如果 i 指针扫描到S串结束位置，或者 j 指针扫描到T串的结束位置，都应该结束查找
  while (i < s.length && j < t.length) {
    if (s[i] == t[j]) {
      // 如果 s[i] == t[j]，则当前位置匹配成功，继续匹配下一个位置
      i++;
      j++;
    } else {
      // 如果 s[i] != t[j]，则说明当前位置匹配失败，
      // 根据KMP算法，我们只需要回退T串的 j 指针到 next[j-1]位置,即最长相同前缀的结束位置后面一个位置，而S串的 i 指针保持不动
      if (j > 0) {
        j = next[j - 1];
      } else {
        // 如果 j = 0,则说明S子串subS和T在第一个字符上就匹配不上, 此时T不匹配字符T[j]前面已经没有前后缀了，因此只能匹配下一个S子串
        i++;
      }
    }
  }

  // 如果最终可以在S串中找到匹配T的子串，则T串的所有字符都应该被j扫描过，即最终 j = t.length
  if (j >= t.length) {
    // 则S串中匹配T的子串的首字符位置应该在 i - t.length位置，因为 i 指针最终会扫描到S串中匹配T的子串的结束位置的后一个位置
    return i - j;
  } else {
    // 否则就是没有在S中找到匹配T的子串
    return -1;
  }
}

function getNext(t) {
  const next = new Array(t.length).fill(0);

  let j = 1;
  let k = 0;

  while (j < t.length) {
    if (t[j] == t[k]) {
      next[j] = k + 1;
      j++;
      k++;
    } else {
      if (k > 0) {
        k = next[k - 1];
      } else {
        j++;
      }
    }
  }

  return next;
}

const s = "aabaabaafaab";
let t = "aabaaf";
console.log(indexOf(s, t));

Python算法源码

def getNext(t):
    next = [0] * len(t)

    j = 1
    k = 0

    while j < len(t):
        if t[j] == t[k]:
            next[j] = k + 1
            j += 1
            k += 1
        else:
            if k > 0:
                k = next[k - 1]
            else:
                j += 1

    return next


def indexOf(s, t):
    """
    :param s: 正文串
    :param t: 模式串
    :return: 在s中查找与t相匹配的子串，如果成功找到，则返回匹配的子串第一个字符在主串中的位置
    """

    next = getNext(t)

    # 手算的T串"cabaa"对应的前缀表
    # next = [0, 0, 0, 0, 0]

    i = 0  # 扫描S串的指针
    j = 0  # 扫描T串的指针

    # 如果 i 指针扫描到S串结束位置，或者 j 指针扫描到T串的结束位置，都应该结束查找
    while i < len(s) and j < len(t):
        # 如果 s[i] == t[j]，则当前位置匹配成功，继续匹配下一个位置
        if s[i] == t[j]:
            i += 1
            j += 1
        else:
            # 如果 s[i] != t[j]，则说明当前位置匹配失败
            # 根据KMP算法，我们只需要回退T串的 j 指针到 next[j-1]位置,即最长相同前缀的结束位置后面一个位置，而S串的 i 指针保持不动
            if j > 0:
                j = next[j - 1]
            else:
                # 如果 j = 0,则说明S子串subS和T在第一个字符上就匹配不上, 此时T不匹配字符T[j]前面已经没有前后缀了，因此只能匹配下一个S子串
                i += 1

    # 如果最终可以在S串中找到匹配T的子串，则T串的所有字符都应该被j扫描过，即最终 j = t.length
    if j >= len(t):
        # 则S串中匹配T的子串的首字符位置应该在 i - t.length位置，因为 i 指针最终会扫描到S串中匹配T的子串的结束位置的后一个位置
        return i - j
    else:
        # 否则就是没有在S中找到匹配T的子串
        return -1


if __name__ == '__main__':
    s = "aabaabaaf"
    t = "aabaaf"
    # t = "cabaa"  # 该T串用于测试第一个字符就不匹配的情况

    print(indexOf(s, t))