浮点格式
在 IEEE-754 浮点标准中,一个数值由 3 部分组成:符号位(S)、阶码(E)和尾数(M)。除了某些例外,每个(S、E、M)模式根据下列格式可以标示一个唯一的数值:
v a l u e = ( − 1 ) S × 1. M × 2 E − b i a s value = (-1)^S \times 1.M \times {2^{E-bias}} value=(−1)S×1.M×2E−bias
S: S = 0 时表示是一个正数,S = 1 时表示是一个负数。
E: 位于浮点数的尾数字段,其值在 0 和 1 之间。
M: 位于浮点数的指数字段,表示小数点的位置。
M 的规范化表示
上面的公式中要求所有的数值都被处理成 1.M 这种形式,这样对于每个浮点数,它的尾数都是唯一的。例如 0.5D(十进制,decimal) 允许的唯一尾数是 M = 0:
0.5 D = 1.0 B × 2 − 1 0.5D = 1.0B \times 2^{-1} 0.5D=1.0B×2−1
其他的形式如 0.1 B × 2 0 0.1B \times 2^{0} 0.1B×20 和 10.0 B × 2 − 2 10.0B \times 2^{-2} 10.0B×2−2 都不行。1.M 格式形式的数称为规格化数(Normalized Numbers)。规格化数都有 1.0 所以存储浮点数时将 1.0 省略。
E 的余码表示
如果 IEEE 中阶码 E 采用 e 位来表示,那么对于阶码在二进制补码表示法的基础上加上 2 e − 1 − 1 2^{e-1} -1 2e−1−1 就构成它的余码表示法。用余码表示的好处是可以无符号比较器比较有符号数。例如 3 位阶码的余码表示:
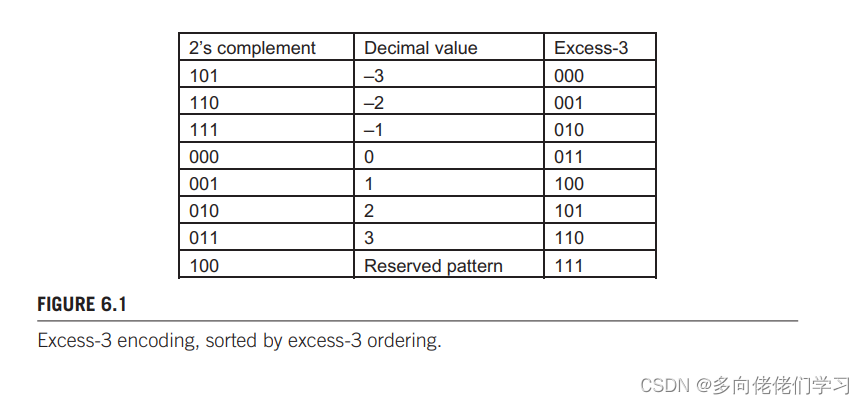
Excess-3 表示余 3 码,即在二进制补码的基础上加上 2 3 − 1 − 1 = 011 2^{3-1}-1=011 23−1−1=011。对余三码进行无符号数的大小比较即可得到对应二进制补码数的大小,速度比有符号数大小比较要快。
0.5D 的 3 位阶码的 6 位格式为:
001000 , 其 中 S = 0 , E = 010 , M = ( 1. ) 00 001 000,其中 S=0,E=010, M=(1.)00 001000,其中S=0,E=010,M=(1.)00
一般而言,采用规格化的尾数和余码表示的阶码,那么带 n 位阶码的数对应的值为:
( − 1 ) S × 1. M × 2 ( E − ( 2 ( n − 1 ) − 1 ) ) (-1)^{S} \times 1.M \times 2^{(E-(2^{(n-1)}-1))} (−1)S×1.M×2(E−(2(n−1)−1))
能表示的数
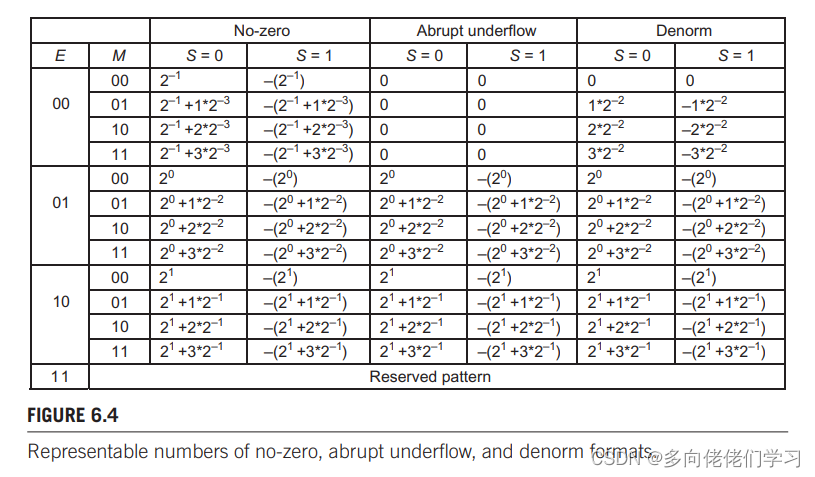
下表列出了 5 位 IEEE 格式的浮点数的表示形式。根据上面的公式应该可以算出非零列(No_Zero)的表示形式如图所示。
非零表示法的正数画在数轴上(负数对称):
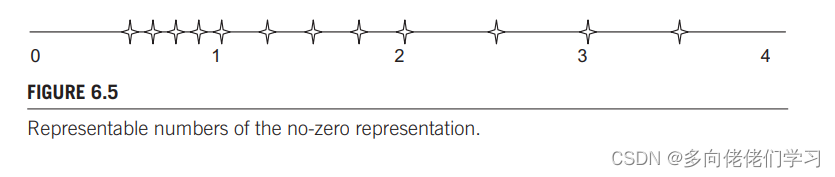
从上两图中可得到 5 个结论:
- 能表示数之间的间隔取决于阶码位。0 的每一边都有三个主间隔,由于阶码有两位和一个模式保留位(11),因此这两个阶码可以形成 3 个不同的位(−2−1 = −0.5D,
−20 = −1.0D, −21 = −2.0D),在左边也有三个对称的。 - 每个主间隔中能表示的数的个数取决于尾数位数,如果为 N 位,则在每个间隔内能表示 2N 个数。
- 这种格式中不能表示0。
- 越靠近 0 的地方,可表示的数离得越近。向 0 的方向移动时,每个间隔的大小是前一个间隔大小的一半。
- 上一条在 0 附近不成立,在 0 附近能表示的数出现了空白。
在规格化浮点表示中,一种容纳 0 的方法是使用下溢出(abrupt underflow),当阶码为 0 时,对应的数为 0,但准确性不行。

实际上,IEEE 标准采用的是非规格化的方法。当 E=0 时,尾数不是 1.XX 这种形式,而是 0.XX 的形式。如果 n 位的阶码是 0,那么这个值是: 0. M × 2 − 2 ( n + 1 ) + 2 0.M \times 2^{-2^{(n+1)+2}} 0.M×2−2(n+1)+2
总之,多增加一个尾数,最大误差可以减少一半,从而提高精度。
特殊的位模式与 IEEE 格式中的精度
如果阶码的所有位都是 1,而尾数是 0,那么该数表示一个无穷大的值。当尾数不为 0 时,表示 NaN。IEEE 浮点格式的所有特殊模式如下图所示。
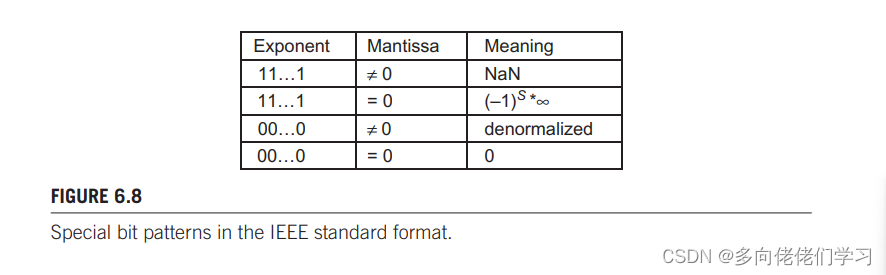
其他的所有数都是规格化的浮点数。单精度浮点数有 1 位符号位、8 位阶码、和23位尾数。双精度有 1 位符号位、11 位阶码和 52 位尾数。双精度浮点数的尾数比单精度多了29位,因此双精度浮点数表示数的最大误差少了 1 / 2 29 1/2^{29} 1/229 倍。由于多了 3 位阶码,双精度浮点数能表示的范围有扩展了很大。
没有意义的操作如 0/0, 0*∞, ∞/∞, ∞–∞ 会产生 NaN,在 IEEE 标准中,NaN 有两种类型:signaling 和 quite。Signaling NaN 通过清零尾数的最高有效位来表示,而 quite NaN 通过置位尾数的最高有效位来表示。
使用 sNaN 作为算术运算的输入会引起异常,使用 qNaN 进行运算得到的结果是 qNaN。
算法的优化
在矩阵乘法中点积运算就需要对输入矩阵两两相乘的结果进行求和。由于加法结合律,这些求和的顺序并不影响加法的结果,但由于浮点精度有限,这些求和顺序会影响最终运算结果的准确度。例如采用 5 位格式表示的 4 个数的和: 1.00 B ∗ 2 0 + 1.00 B ∗ 2 0 + 1.00 B ∗ 2 − 2 + 1.00 B ∗ 2 − 2 1.00B*2^0+1.00B*2^0+1.00B*2^{−2}+1.00B*2^{−2} 1.00B∗20+1.00B∗20+1.00B∗2−2+1.00B∗2−2
如果按照先后顺序:
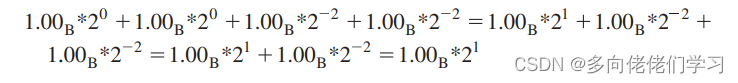
在第二步和第三步中,较小的操作数直接消失了,这是因为与较大的操作数相加时,它比大操作数的最低有效位要小。
采用一种并行算法:
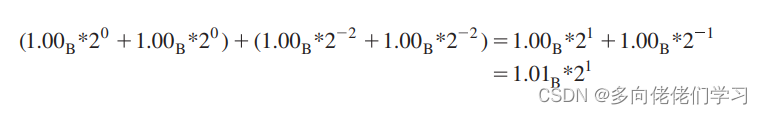
改变顺序后的结果与之前结果不同,因为第 3 项和第 4 项相加的结果不足以让他们丢失。
所以要想使算数运算的准确度达到最大化,通常采用的技术是在归约计算前对数据进行排序。
数值稳定性
先看一个解方程组的例子:

将系数矩阵化成单位阵,可得解:

按上图所示可设计一种高斯消元 kernel 函数,每个线程处理矩阵中一行上要完成的所有计算迭代。每次除法步骤之后,所有线程用 __syncthreads() 同步。然后开始减法运算,减法运算后,所有线程需要再次同步,以确保下一步用到的是更新后的信息。一个线程完成了指定任务就会暂停,直到回代阶段开始。
但是,用简单的高斯消元会遇到数值稳定性问题,例如:

第一行 X 的系数是 0,没法让方程一除以 0,所以上面的算法对于此方程组是数值不稳定的。
因此我们要做初等行变换,改变方程一的位置:
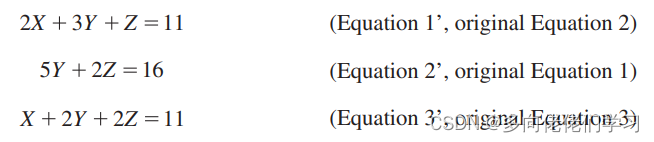
现在的方程一除以2,再用现在的方程三减去方程一。下面就可以用上面方程组的解法来继续了:

一般来说初等行变换选择首变量系数绝对值最大的方程和顶端方程来交换。虽然初等行变换从概念上来说比较简单,但会导致算法实现变得复杂影响性能,在 kernel 中可以为每一行重新分配线程。