目录
写在前面
在上一节,我们以通俗的方式理解了一下概率。
在理解了概率后,我们开始尝试理解概率密度,这是理解贝叶斯法则的前提。
原因很简单,贝叶斯法则推导的是概率密度函数,而不是概率。
1. 核心概念——概率密度
随机变量有两种,非连续性和连续性。
非连续型随机变量,其取值空间不连续,可以是有限个随机事件,也可以是无限多个随机事件。当在可取值的随机事件数量有限时,每一个随机事件可以单独计算概率值。比如,抛硬币要么正面,要么反面,即便考虑硬币落地后站立的特殊情况,也只有3种情况。直接使用概率来表达,显得清晰而自然。
连续型随机变量,顾名思义,它可以在一个连续的区间内任意取值。比如,我们自查体温时,由于仪器本身或是使用方法的不同,可能会得到一系列值,其特点是取值并不局限在特定的数值上。我们无法单独指出某个数据出现的概率,但是可以得出某个区间的概率。
从概率角度来看,它们都可以有概率的定义,只是含义稍微有所不同。但是,若从概率密度角度来讨论,就会出现极大的不同。
那就是,只有连续性随机变量才有概率密度的定义。因为,概率密度函数是对连续性概率分布函数(cdf)的导数,反映的是概率分布的变化情况。
我们这里强调的要点是,贝叶斯概率公式中并未使用概率,而是直接使用概率密度pdf。
1.1 “点概率”没有意义
既然提到了概率分布函数cdf,简单介绍一下。
首先,很多人会走入一个误区——混淆点概率和概率密度。先说结论——对于连续型随机变量,我们不关注“点概率”,只关注“区间概率”。
以一维正态分布举例,如下图蓝线所示,一口光滑的大钟。对于蓝色曲线上的任意一点,可以得到一个概率密度值。

请注意,获得的只是这个点处的概率密度值,而不是点概率值。参考质量与密度的关系,密度是表示质量聚集程度的度量,密度高,在单位空间的质量越大。再看看概率与概率密度,我们可以认为,在单位区间内概率的数值越大。
也许你会问,为什么不计算一下点概率值?这个可从积分角度来理解。单纯一个点,计算积分不是不可以,但结果永远为0(回顾积分公式)。计算某个点处的概率值也是这样,正如,密度之于质量,单个点的质量为0,没有意义。
1.2 概率密度函数怎么用?
设想一下,我们经过一系列推导,最后得到一个概率密度函数。这个函数可以很复杂,复杂到你没法估计出来这个概率密度函数对应的曲线或图形,更没法画出来,我们该怎么改?如果我们强硬地为这个概率密度分布套在已知的模型里,比如正态分布,那么结果是否可以简化地表达?
与之对应,有两种概率密度函数的用法。
第一种,不理会随机事件x的概率密度函数的具体形态,可能是因为复杂,也可能是不关注整体的分布,而是以最优化方式寻找最大概率密度处所对应的取值,并直接把这个值作为随机事件x的最优估计。这种思路类似于频率学派的做法,比如,使用经典的概率模型去做重复性试验,得到一个统计概率,找到发生频率最高的事件取值作为这类试验的预估值。
第二种方式比较特别,对某些人群而言,也许更自然一些。它不关注随机事件x的每个具体取值,而是关注随机事件x的整个取值空间,以及对应的概率密度分布。(注意:不一定是高斯分布的,也可以是其他小众分布)用白话讲,我没法给你一个准确答案,但我能给你圈一个空间,并给出空间中每种取值的概率情况。
总结一下,第一种用法属于寻优法,希望给出最大概率密度下的确定结果(或者最大概率密度对应的点)。而后一种用法常用于概率推导,给出一个区间(注:正负无穷之间也是一个区间),并给出在这个区间的概率密度情况。
初一看,前者直接给出所谓的最优值,而后者要给出一个概率密度分布,似乎后者信息量更大,表达起来更复杂。但是,如果选择正态分布,这种优雅、对称和简洁的分布形式,你会发现,后一种表达也可以表达得很精炼。卡尔曼滤波就是很好的例子。(挖个坑,以后说。)
2. 无人车里的“贝叶斯法则”
贝叶斯法则,也叫贝叶斯概率密度公式。记住他的名字——Bayes,方便以后进行扩展阅读。
在理解概率密度的含义之后,我们就可以愉快地理解贝叶斯法则。特别地,我们将在无人车状态识别的大背景下来理解。
在拆解贝叶斯法则前,先看看这个简洁、优美而对称的公式。
欣赏之后,我们开始讨论公式的每个部分。
2.1 联合概率密度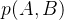
为什么突然说到联合概率?在贝叶斯法则里,并没有出现联合概率密度啊!?
我这里没有搞错。贝叶斯法则本身就是从联合概率密度推导而来。
顾名思义,联合概率表达的是两个随机变量同时发生的概率。为了加强对概念的理解,先来做一个练习。
在无人车的测量模型里,A是传感器测量值y,B是车子在当前时刻的位姿x。因此,联合概率表示当车子位姿为x,测量值为y时的概率密度值。
再做一个练习,在无人车的运动模型里,A是车子在当前时刻的位姿xt,而B由两种状态量组成,分别是车子在上一时刻的位姿xt-1和当前时刻的运动增量v,所以联合概率p(xt,xt-1,v)表示当车子在本时刻、上一时刻位姿和运动增量分别是xt,xt-1和v时的概率密度值。
这种练习看起来很简单,反复练习有助于理解概率密度的所指,增加贝叶斯推导的熟练度。
2.2 先验概率: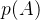
不要被名字唬住了,他只是一个概率而已。
通俗地讲就是,一个“自以为是”的概率,完全是基于有限的知识与信息或经验而来。至于获得的方式,可以是根据经验而得的概率,由自己总结,或者由设备的供应商提供(他们其实也是经过大量重复实验获得的频率值),或者是在连续推导过程的上一步计算而得。带有很多的主观性。
比如,在无人车系统里,表示当前时刻无人车位姿为x的概率值。
表示最近一次传感器测量值为y的概率值。
2.3 条件概率 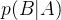
条件概率也很好理解。大意是,在已知条件A的前提下,我们对随机事件B的确信程度。
还是拿无人车的测量模型来举例,表示当无人车当前时刻的位姿是x时,获得传感器测量数据为y的概率值。在有些资料里,也称作传感器测量的概率模型。
2.4 边缘概率 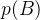
“边缘概率”的名称来源于手算离散型边缘概率的计算过程。当的每个值被写在m行n列的网格中时,对网格中的每行求和是很自然的事情,然后将求和的结果P ( m )写在每行右边的纸的边缘处。注意:这里出现了与“边缘”呼应的字眼。
对于连续型变量,我们需要用积分替代求和:
p(b)=∫p(b,a)da
含义与离散型随机变量的边缘概率计算方法一样。对于任意随机事件b,计算已知b,且a,b同时发生的概率值(在已知b的情况下,计算联合概率密度的积分)。
很有可能,当接触到这个专业术语时,你会觉得很费解。(在SLAM里,等你接触到BA大法,也有个类似的概念叫边缘化,也会同样难理解。先挖个坑,后续SLAM里再展开。)我的理解是,这个概率是联合概率的上限,因为我们知道条件概率的值必定小于1,根据联合概率的定义,必定有
当然你也可以说p(A)也能叫做边缘概率。只是一个专业名称而已。
在无人车系统里,p(B)与p(A)的理解方式类似,不做赘述。
2.5 后验概率 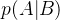
很明显,后验概率与先验概率相对。通俗地讲就是,马后炮。
当有了结果后,又去讨论原因。或者说,根据结果来分析原因。在贝叶斯概率推导中,通常是说,当观察者的知识或信息增加B后,对随机事件A发生的概率,它是对随机事件先验概率p(A)的一种更新,反映了观察者知识或信息的变化情况。
在无人车系统里, 常见的后验概率有p(x|y),表示当传感器测量信息为y时,无人车位姿为x的概率。特别地, P(xt|xt-1,v)表示当无人初始位姿为xt-1,且经过运动增量v之后,无人车的更新位姿为xt的概率值。也可以认为是无人车状态转移(或称运动)的概率模型。
最后的话
重要的事情说三遍。
在贝叶斯法则里,使用的是概率密度函数,而不是概率。
在贝叶斯法则里,使用的是概率密度函数,而不是概率。
在贝叶斯法则里,使用的是概率密度函数,而不是概率。
而对于概率密度函数,有许多专业名词,第一次接触时很拗口,有距离感。但仔细揣摩一下,会发现,也都是很自然的命名法。
这就是我所理解的无人车看世界的底层逻辑。
希望对你有所启发和帮助。