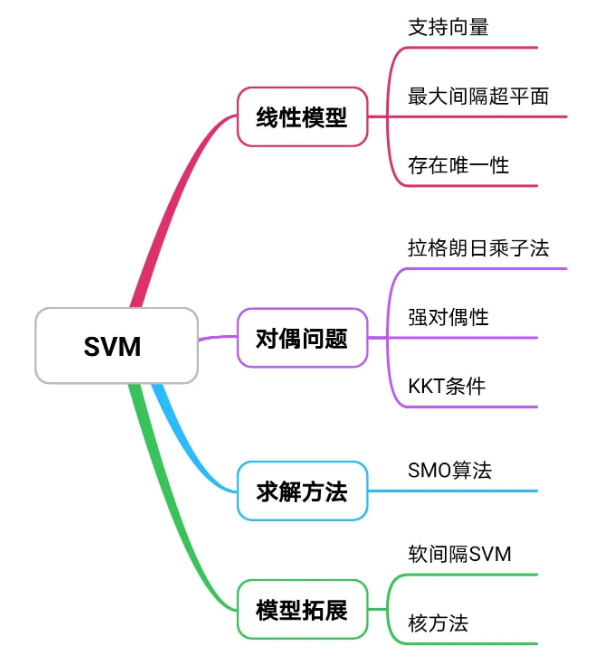
机器学习 —— 通俗易懂的解释支持向量机

本文主要内容如下：

SVM原始模型构建
对偶形式的推导
求解的方法
软间隔SVM及核方法
SVM 优缺点及应用

什么是 SVM

首先，让我们来对 SVM 产生一个直观的认识：支持向量机(Support Vector Machine,SVM)，二类分类器，它最终能告诉你一个东西是属于 A 还是属于 B。在由样本点构成的向量空间内，SVM 通过找到一个可以将两类数据正确分隔在两侧的划分超平面，达到对数据分类及预测的效果。而这个超平面是通过支持向量确定的，机的意思呢就是算法，故支持向量机就是通过支持向量确定划分超平面，从而做到分类及预测的算法

什么是超平面？

超平面是指 n 维线性空间中维度为 n-1 的子空间。它可以把线性空间分割成不相交的两部分。比如二维空间中，一条直线是一维的，它把平面分成了两块；三维空间中，一个平面是二维的，它把空间分成了两块

在样本空间中，划分超平面可通过线性方程 \(w^tx + b = 0\) 来描述，其中 \(w = (w_1,w_2,……,w_d)\) 为法向量，决定超平面的方向；\(b\) 为位移项，决定超平面与原点之间的距离。一个划分超平面就由法向量 \(w\) 和位移 \(b\) 确定

一、SVM 原始模型构建

1.1 线性SVM模型

SVM 由线性分类开始，所以我们首先来了解一下什么是线性可分。简单来说，在二维空间上，两类点能够被一条直线完全分开则叫做线性可分。如下图左边是线性不可分的，而右边即为线性可分

数学上我们可以表述为：对于 n 维欧氏空间中的两个点集 \(D_0\) 和 \(D_1\)，若存在 \(n\) 维向量 \(w\) 和实数 \(b\)，使得：\(\forall x_i\in D_0\) 满足 \(w^Tx_i+b>0\)，而 \(\forall x_j\in D_1\) 满足 \(w^Tx_j+b<0\)，则称 \(D_0\) 和 \(D_1\) 线性可分

1.1.2 支持向量与最大化间隔

给定线性可分的训练样本集 \(T=\{(x_1,y_1),(x_2,y_2),...,(x_m,y_m) \},y_i\in\{-1,1 \}\) ，线性分类器将基于训练样本 \(T\) 在二维空间中找到一个超平面来正确划分两类样本。显然，满足条件的超平面有很多，而我们旨在找到鲁棒性最好的

“鲁棒”是“ Robust ”的音译，也就是健壮的意思。由于训练样本集的局限性或噪声因素，训练集之外的样本可能会更接近两个类的分隔界，这将导致很多划分超平面出现错误。所以我们想要找到与两类数据间隔最大的超平面，使之对训练集之外的数据或噪声有最大的“容忍”能力

首先，我们要明确该模型中“距离”的概念。由于划分超平面并不确定，所以我们需要比较同一个点到不同超平面的距离，为了使之具有可比性，我们使用欧式几何距离。

相信大家不陌生的是，一个二维空间点 \(p=(x_p,y_p)\) 到直线 \(Ax+By+C=0\) 的距离公式为：

\[r=\frac{|Ax_p+By_p+C|}{\sqrt[]{ {A^2+B^2}}} \]

而扩展到 \(n\) 维空间后，点 \(x=(x_1,x_2,...,x_n)\) 到超平面 \(w^Tx+b=0\) 的距离公式为：\(r=\frac{|w^Tx+b|}{||w||}\) ,其中 \(||w||=\sqrt[]{w_1^2+w_2^2+...+w_n^2}\)

既然我们要找出与两类数据间隔最大的划分超平面，很直观地就会考虑从两类数据最靠近的地方下手，因为它们各自最边缘位置的点才有可能成为最靠近划分超平面的那几个点，而其他点对确定超平面的最终位置是起不了作用的，所以我们认为是这些边缘点支持了超平面的确立。而在数学里点又可以叫向量，比如二维点 (x, y) 就可以看成是一个二维向量，同理 n 维点就是一个 n 维向量，所以我们将这些有用的边缘点称为“支持向量”(support vector)

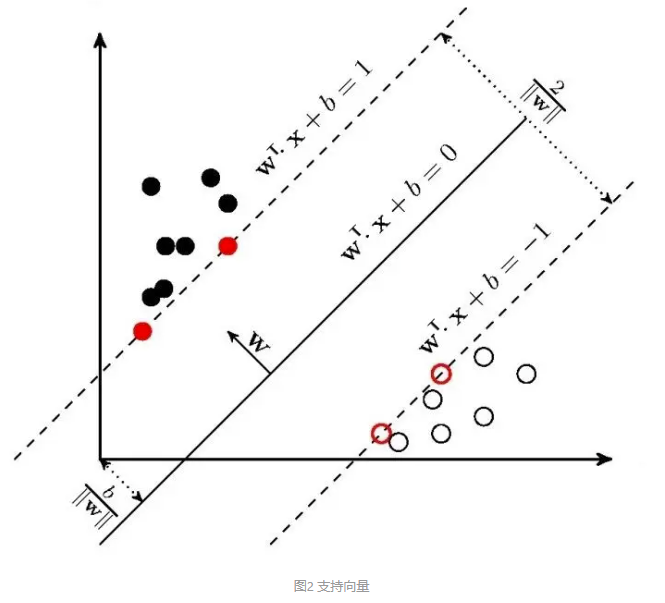
如图所示，标红的点就是支持向量，它们确定出了两条虚线，我们称之为“支撑超平面”，并将它们之间的距离称为“间隔”(margin)，用希腊字母表示，而它们“正中间”的位置就是我们要找的最优划分超平面的位置。显然，间隔越大我们的划分超平面鲁棒性就越好。所以在开始推导 SVM 的原始公式之前，请在脑海里跟我默念三遍 SVM 的核心思想 —— “ 最大化间隔！”

1.2 SVM 原始公式导出

假设超平面 \((w,b)\) 能将训练样本 \(T\) 正确分类，那么任一数据点 \((x_i,y_i)\) 到该超平面的距离为：

\[r_i=\frac{|w^T{x_i}+b|}{||w||} \]

显然 \(||w||>0\)，否则超平面变为 \(b=0\)，失去意义

考虑到此式中含有绝对值会对后续数学计算带来不便，所以我们利用数据点自带的标签y_i去绝对值。结合1.1.1中讲过的线性可分的数学定义可知：

\[\begin{cases}{w^Tx_i+b>0，\ \ \mathrm{if}\ \; y_i>0}\\{w^Tx_i+b<0，\ \ \mathrm{if}\ \; y_i<0} \end{cases} \]

所以任一数据点到超平面的距离可表示为：

\[r_i=\frac{y_i(w^T{x_i}+b)}{||w||}>0 \]

则最接近超平面的距离为：

\[d=\min \limits_i\frac{y_i(w^Tx_i+b)}{||w||} \]

调整平面位置，找到最大距离：

\[d^*=\max\limits_{w,b}\min\limits_i \frac{y_i(w^Tx_i+b)}{||w||} \]

则最大间隔为：

\[\gamma=2d^*=2\max\limits_{w,b}\min\limits_i \frac{y_i(w^Tx_i+b)}{||w||} \]

至此，我们已经将问题用数学语言表述出来了，即要找到一组使得 \(\gamma\) 最大的 \((w^*,b^*)\) 确立最优划分超平面，但形式上任较为复杂

我们知道，对于二维空间中的一条直线 \(Ax+By+C=0\)，等比例地放缩 \(A、B、C\) 是不影响它的位置的，比如 \(kAx+kBy+kC=0\) 仍代表同一条直线

扩展到 \(n\) 维空间中，等比例地放缩 \(w、b\) 也是不影响解平面 \(w^Tx+b=0\) 位置的。又已知 \(y_i(w^Tx_i+b)>0\)(超平面外一点与之距离大于0得出)，所以我们不妨令 \(\gamma\) 表达式中的 \(\min\limits_iy_i(w^Tx_i+b)=1\)，则问题简化为，求：

\[\max\limits_{w,b}{\frac{2}{||w||}}\\ \mathrm{s.t.}\quad y_i(w^Tx_i+b)\ge1,\ i=1,2,...,m \]

显然，最大化 \(\frac{1}{||w||}\) 等价于最小化 \({||w||}^2\)，为了便于求导，我们继续将问题转化为，求：

\[\min\limits_{w,b}\frac{1}{2} { {||w||}^2}\\ \mathrm{s.t.}\quad y_i(w^Tx_i+b)\ge1,\ i=1,2,...,m \]

至此，我们便得到了SVM的基本型

1.3 算法小结

接下来，我们就从理论上验证它的可行性

1.3.1 SVM 最大间隔划分超平面的存在唯一性

定理：若训练数据集线性可分，则可将中的样本点完全正确分开的最大间隔划分超平面存在且唯一。

证明：
(1)存在性

由于训练数据集线性可分，又目标函数存在下界，所以必存在最优解，由此得知最大间隔划分超平面的存在性

(2)唯一性

首先证明最优解中 \(w^*\) 的唯一性。假设存在两个最优解 \((w_1^*,b_1^*)\) 和 \((w_2^*,b_2^*)\) ，由目标函数的形式可知必有 \(||w_1^*||=||w_2^*||=c\)，其中c是一个常数。令 \(w=\frac{ {w_1^*+w_2^*}}{2},b=\frac{b_1^*+b_2^*}{2}\)，则 \((w,b)\) 必然也是一个可行解，试想两个可正确划分样本点的超平面中间夹的一个超平面必然也可以正确划分样本点。但由于 \((w,b)\) 不一定是最优解，则有

\[c\le||w||\le\frac{1}{2} ||w_1^*||+\frac{1}{2} ||w_2^*||=c \]

中间那个“ \(\le\) ”关系由 “三角形两边之和大于第三边” 拓展到 n 维得到

由上式可得， \(||w||=\frac{1}{2}||w_1^*||+\frac{1}{2}||w_2^*||\) ，从而有 \(w_1^*={\lambda}w_2^*\) ， \(|\lambda|=1\) (想象若强行令三角形两边之和等于第三边，则三条线段将会共线)。若 \(\lambda=-1\) ,则 \(w=0\)，与 \((w,b)\) 是可行解相矛盾；因此必有\(\lambda=1\)，则 \(w_1^*=w_2^*，w^*\) 的唯一性得证

接下来证明 \(b^*\) 的唯一性。假设存在两个最优解 \((w^*,b_1^*)\) 和 \((w^*,b_2^*)\) ，不妨设 \(x_1\) 和 \(x_2\) 对应的 \(y\) 值都为1，且它们分别是两个最优解的支撑超平面上的点，满足与自己对应的划分超平面距离为 \(\frac{1}{||w||}\)，即满足

\[\begin{cases}w^*x_1'+b_1^*=1\\ w^{*}x_2'+b_2^*=1\end{cases} \]

同时与另一个划分超平面距离大于等于 \(\frac{1}{||w||}\)，即

\[\begin{cases}w^*x_2'+b_1^*\ge1\\{w^{*}x_1'+b_2^*\ge1} \end{cases} \]

整理得出

\[{\begin{cases}w^*x_2'+b_1^*\ge{1}=w^*x_1'+b_1^*\\{w^{*}x_1'+b_2^*\ge{1}=w^*x_2'+b_2^*}\end{cases}} \Rightarrow{\begin{cases}w^*x_2'\ge{w^*x_1'}\\{w^*x_1'\ge{w^*x_2'}}\end{cases}} \]

所以

\[w^*x_2'={w^*x_1'} \]

带入第一对等式方程即可得 \(b_1^*=b_2^*\)，则 \(b^*\) 的唯一性得证

至此，我们得知 SVM 基本型的最优解存在且唯一

1.3.2 小结

线性可分支持向量机——最大间隔法(maximum margin method)

输入：线性可分训练数据集 \(T=\{(x_1,y_1),(x_2,y_2),...,(x_m,y_m) \}\),其中 \(x_i\in R^n,y_i\in\{-1,1 \},i=1,2,...,m\)

输出：最大间隔划分超平面和分类决策函数

(1)构造并求解约束最优化问题：

\[\min\limits_{w,b}\frac{1}{2} { {||w||}^2}\\ \mathrm{s.t.}\quad y_i(w^Tx_i+b)-1\ge0,\ i=1,2,...,m \]

求得最优解 \(w^*,b^*\);

(2)由此得到划分超平面：

\[w^{*T}x+b^*=0 \]

分类决策函数：

\[f(x)=\mathrm{sign}(w^{*T}x+b^*) \]

二、对偶形式的推导

首先顺带一提，上面的基本型是一个凸二次规划问题，可以直接用现成的优化计算包求解。但若利用“对偶问题”来求解会更高效，所以我们来推导 SVM 的对偶形式

什么是凸优化问题

直观来说就是在定义于凸集中的凸函数上求最小值。但需要注意的是，国内关于函数凹凸性的定义和国外是相反的，这里的凸函数是指开口向上的。由凸集和凸函数的定义可得出，凸优化问题具有一个极好的性质，即局部最优值必定是全局最优值，因为它不管是局部还是全局都只有那一个最优值。(实际上这个性质叫做强对偶性，且需满足一定的条件才能具备，我这里为了方便理解讲得比较牵强，想具体了解的可点开链接)

什么是二次规划问题

如果一个问题的目标函数是变量的二次函数，约束条件是变量的线性函数，我们将其称为二次规划问题

2.1 拉格朗日函数

拉格朗日函数是拉格朗日乘子法的核心组成部分，此法思想为：将有约束优化问题从形式上转化为等价的无约束优化问题(建议对此法陌生的同学进去看看图文并茂的讲解)

优化问题存在很多形式，比如目标函数有求最大值的，也有求最小值的；约束条件有用大于式表示的，也有用小于式的。而上面说到凸优化问题具有“局部最优值必定是全局最优值”这一良好性质，所以我们可以通过移项将SVM基本型写成凸优化问题的标准形式

\[\begin{array}{lcl}\, \min\limits_x\quad \,\, f\; (x)\,,\ x \in R^{\, n} \\ \,\;\mathrm{s.t.} \quad\,\; g_i(x)\le0,{\ } i=1,2,..., p \\ \qquad \quad \,\, h_j(x)=0,\ j=1,2,...,q\end{array} \]

SVM原始形式：

\[\begin{array}{lcl}\,\,\min \limits_{w,b} \ \ \,\, \frac{1}{2}{||w||}^2 \\ \ \ \,\mathrm{s.t.}\quad y_i(w^Tx_i+b)-1\ge 0,\ i=1,2,...,m \end{array} \]

只含有不等式约束，将其改写成：

\[\begin{array}{lcl} \ \min \limits_{w,b} \ \ \,\, \frac{1} {2}{||w||}^2 \\ \ \ \,\mathrm{s.t.}\quad 1-y_i(w^Tx_i+b) \le 0,\ i=1,2,...,m \end{array} \]

则其拉格朗日函数为：

\[\begin{align}&\mathcal{L}(w,b,\alpha)={ \frac{1}{2}}{||w||}^2 + {\sum_{i=1}^{m}\alpha_i[1-y_i(w^Tx_i+b)]} \\&\;\mathrm{s.t.}\quad \alpha_i\ge0,\ i=1,2,...,m \end{align} \]

接下来到了关键的一步，所以我们需要再明确一遍，将问题改写成拉格朗日函数仅仅只是从形式上改变它，而实质上必须是等价的。那么接下来我要说明以下两个问题是等价的：
① 求 \({\frac{1}{2}} {||w||}^2\)，在 \(1-y_i(w^Tx_i+b)\le0,\ i=1,2,...,m\) 这个条件下；
② 求 \(\max\limits_{\alpha}\mathcal{L}(w,b,\alpha)\)，在 \(\alpha_i\ge0,\ i=1,2,...,m\) 这个条件下；

从问题②入手，当它满足自身约束条件时，拉格朗日函数 \(\mathcal{L}(w,b,\alpha)\) 表达式中的累加项内容为非负常数 \(\alpha_i\) 和 \([1-y_i(w^Tx_i+b)]\) 的乘积，那么欲求其最大值必须满足 \([1-y_i(w^Tx_i+b)]\le0\)，否则调整 \(\alpha_i\) 可以达到无穷大，失去意义，所以我们发现问题②是自带问题①的约束条件的(这里希望读者可以从中体会原始规定不等式约束的拉格朗日乘子 \(\alpha_i\ge0\) 的巧妙)

接下来我们会注意到, \(\begin{array}\ \sum_{i=1}^{m}\alpha_i[1-y_i(w^Tx_i+b)] \end{array}\) 作为一个非正项，其最大值就是0，所以求 \(\max\mathcal{L}(w,b,\alpha)\) 的值就是求 \({\frac{1}{2}} {||w||}^2\) 的值。至此，我们发现问题②是与问题①等价的

所以我们可以将原问题做如下转变

\[\begin{array}{lcl} \ \min \limits_{w,b} \ \ \;\; {\frac{1}{2}}{||w||}^2 \\ \ \ \, \mathrm{s.t.}\quad \ 1-y_i(w^Tx_i+b)\le0,\ i=1,2,..., m\end{array}\\ \Big\Downarrow\\ \begin{array}{lcl}\min\limits_{w,b} \max\limits_{\alpha}\ \ \mathcal{L}(w,b,\alpha) \\\,\mathrm{s.t.}\quad \ \alpha_i\ge0,\ i=1,2,...,m\end{array} \]

这时我们再用上凸优化问题的强对偶性，即不管局部还是全局都只有同一个最优解，可将极小极大的求解顺序换成求极大极小以便于运算：

\[\begin{array}{lcl} \max\limits_{\alpha}\min\limits_{w,b}\ \ \mathcal{L}(w,b,\alpha) \\ \,\mathrm{s.t.}\quad\ \, \alpha_i\ge0,\ i=1,2,...,m \end{array} \]

2.2 KKT 条件

前面点开了朗格朗日乘子法这个链接的同学可能会发现，其中介绍的是仅含有等式约束的优化问题。实际上此法的原始形式中就只包含等式约束，而为了将其泛化到可求带有不等式约束的优化问题，我们引入 KKT 条件

2.2.1 不等式约束

首先来看不等式约束优化问题最简单的形式：

\[\begin{array}{lcl} \min\limits_x \;\; \, f(x)\,,\ x \in R^{\, n} \\ \, \mathrm{s.t.}\quad g(x)\le0 \end{array} \]

其对应的拉格朗日函数为：

\[\mathcal{L}(x,\alpha)=f(x)+\alpha g(x)\,,\ \alpha \ge0 \]

我们利用图形来对其产生一个直观的认识：

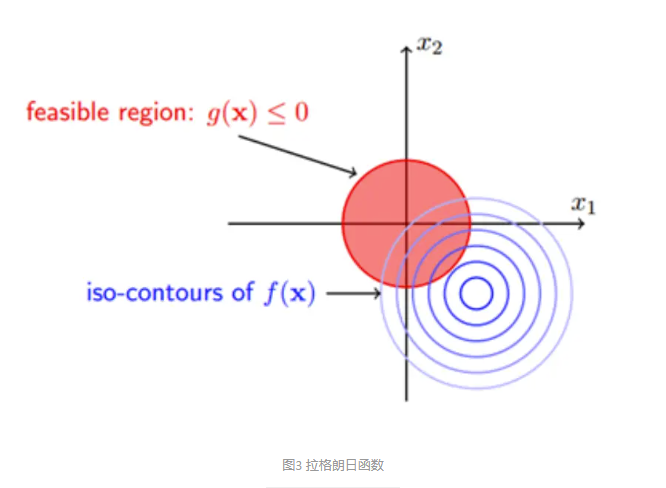
图中画出了目标函数 \(f(x)\) 的等高线和约束区域 \(g(x)\) ，我们的可行解(相当于局部最优解，在凸优化中即必为最优解)需落在约束区域内，且最接近 \(f(x)\) 的 “中心”，即无约束解。至于无约束解和约束区域的相对位置，有以下两种可能：

①无约束解落在约束区域内

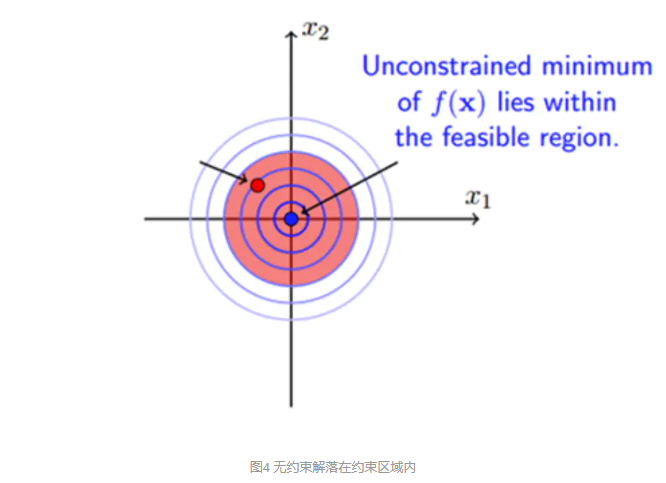
此时，可行解 \(x\) 在g \((x)<0\) 内取到无约束解，必然满足 \(g(x)\le0\)，相当于失去这一约束，即 \(\mathcal{L}(x,\alpha)\) 中的拉格朗日乘子 \(\alpha\) 取为0

②无约束解落在约束区域外

此时，可行解x必然落在约束区域的边界上，即满足 \(g(x)=0\)。至此我们可以得到一个重要的结论(记为“结论*”)，即无论哪种情况下都有：

\[\alpha \,g(x)=0 \]

接着继续考虑可行解 \(x\) 落在边界上的位置，为了尽量靠近无约束解，直观上我们就可以看出，必然要取无约束解与约束区域中心的连线交于边界上的那一点。从函数梯度方面来考虑的话，目标函数的负梯度方向(下图中蓝色小箭头 \(\color{blue}\rightarrow\) )应远离约束区域朝向无约束解，即我们要找到目标函数的负梯度方向与约束函数的梯度方向( \(\color{red}\rightarrow\) )相同的那一点：

\[-\nabla_xf(x)=\alpha\,\nabla_xg(x),\ \ \alpha>0 \]

也即：

\[\nabla_x\mathcal{L}(x,\alpha)=\nabla_xf(x)+\alpha\,\nabla_xg(x)=0,\ \ \alpha>0 \]

这里我想举一个例子帮助大家理解：假设山坡上有一只被圈养的小羊，它想去山顶看看，但不幸的是有一圈栅栏限制了它的活动范围。所以它只能沿着栅栏走到尽可能靠近山顶的位置，然后望着山顶咩咩叹气。这里的山顶便是目标函数的无约束解，栅栏便是约束函数的边界，此时羊头的朝向一定是指向山顶的，且与栅栏的梯度同向

什么是梯度

一个向量，指向函数值上升最快的方向。假如你是那只小羊，在山坡上朝四面八方走都可以，而每个方向你都可以判断出山坡的陡峭程度，即各个方向上你都可以求得方向导数，其中值最大的那个叫做梯度。补充一句，当偏导数连续时才有梯度的存在。
关于梯度，还有一个很直观的例子，想象一滴水沿着光滑的玻璃往下流动，其运动轨迹的反方向即是玻璃表面的梯度方向

2.2.2 形式化的KKT条件

回到凸优化问题的标准形式：

\[\begin{array}{lcl}\, \min\limits_x\quad\; \, f\; (x)\,,\ x \in R^{\, n} \\ \,\;\mathrm{s.t.} \quad\ \; g_i(x)\le0,{\ } i=1,2,..., p \\ \qquad \quad \,\, h_j(x)=0,\ j=1,2,...,q\end{array} \]

回到凸优化问题的标准形式：

\[\begin{array}{lcl}\, \min\limits_x\quad\; \, f\; (x)\,,\ x \in R^{\, n} \\ \,\;\mathrm{s.t.} \quad\ \; g_i(x)\le0,{\ } i=1,2,..., p \\ \qquad \quad \,\, h_j(x)=0,\ j=1,2,...,q\end{array} \]

结合之前的分析，我们将可行解 \(x\) 需满足的条件汇总，即为“ KKT 条件”(Karush-Kuhn-Tucker Conditions)：

\[\qquad \quad\ \,\;\,\nabla_x\mathcal{L}(x,\alpha,\beta)=0 ①\\ \qquad \qquad \qquad \quad\ \ \ \ \ \alpha_i \ge0,\;{\ } i=1,2,..., p ②\\ \qquad \qquad \qquad\ \;\;\,\, g_i(x)\le0,\ {\ } i=1,2,..., p ③\\ \qquad \qquad \qquad\quad h_j(x)=0,\,\, j=1,2,...,q ④\\ \qquad \qquad \qquad \alpha_i\,g_i(x)=0,\ {\ } i=1,2,..., p ⑤ \]

这一组方程看似很复杂，但其实很好理解

①式：拉格朗日函数取得可行解的必要条件(羊爬山的例子)

②式：不等式约束对应的拉格朗日乘子的初始条件

③~④式：优化问题的初始约束条件

⑤式：前面得到的那个重要“结论”

总结一下，KKT 条件是“一个凸优化问题存在最优解”的充要条件，通过 KKT 条件我们即可求得凸优化问题的最优解。用数学语言表述一下就是：

若目标函数 \(f(x)\) 和不等式约束 \(g_i(x)\) 都是凸函数，而等式约束 \(h_i(x)\) 是仿射函数(即形如 \(w^Tx+b=0\) 的线性函数)，且不等式约束 \(g_i(x)\) 的等号都能成立(这一条件称为 \(Slater\) 条件)，那么满足 KKT 条件的 \(x\) 点即为全局最优解

2.3 SVM的对偶形式

在引入 KKT 条件之前，我们已经将 SVM 转化成了如下形式:

\[\begin{array}{lcl} \qquad\quad\ \, \max\limits_{\alpha}\min\limits_{w,b}\ \ \mathcal{L}(w,b,\alpha) \\ \qquad \quad\ \ \; \mathrm{s.t.}\quad\alpha_i\ge0,\ i=1,2,...,m \end{array} \]

其中

\[\mathcal{L}(w,b,\alpha)={\frac{1}{2}}{||w||}^2+\sum_{i=1}^{m}\alpha_i[1-y_i(w^Tx_i+b)] \]

我们发现，求解 \(\min\limits_{w,b}\mathcal{L}(w,b,\alpha)\) 是可以利用 KKT 条件的

对于条件①：\(\nabla_x\mathcal{L}(x,\alpha,\beta)=0\)，我们这里的变量为 \(w\) 和 \(b\)，所以有：

\[\nabla_{w,b} \mathcal{L}(w,b,\alpha)=0 \quad\Longrightarrow \quad \frac{\partial \mathcal{L}}{\partial w}=0\,,\ \frac{\partial \mathcal{L}}{\partial b}=0 \]

那么接下来我们就可以进行一波愉快的数学计算了。。。(还没学过向量函数求导的小伙伴们，快进来现学一下吧~)

\[\begin{align} \frac{\partial \mathcal{L}}{\partial w}=0 &=\frac{\partial}{\partial w}[ \frac {1}{2} w^Tw+\sum_{i=1}^{m}\alpha_i-\sum_{i=1}^{m}\alpha_iy_i(w^Tx_i+b)]\\ &=\frac{\partial}{\partial w}(\frac {1}{2} w^Tw+\sum_{i=1}^{m}\alpha_i-\sum_{i=1}^{m}\alpha_iy_i w^Tx_i-\sum_{i=1}^{m}\alpha_iy_ib )\\ &=\frac{\partial}{\partial w}(\frac {1}{2} w^Tw-\sum_{i=1}^{m}\alpha_iy_i w^Tx_i )\\ &=\frac{\partial}{\partial w}(\frac {1}{2} w^Tw-w^T\sum_{i=1}^{m}\alpha_iy_i x_i )\\ &=w-\sum_{i=1}^{m}\alpha_iy_i x_i \end{align} \]

\[\begin{align} \frac{\partial \mathcal{L}} {\partial b}=0&=\frac{\partial} {\partial b}[ \frac {1}{2} w^Tw+\sum_{i=1}^{m}\alpha_i-\sum_{i=1}^{m}\alpha_iy_i(w^Tx_i+b) ] \\ &=\frac{\partial}{\partial b}(\frac {1}{2} w^Tw+\sum_{i=1}^{m}\alpha_i-\sum_{i=1}^{m}\alpha_iy_i w^Tx_i-\sum_{i=1}^{m}\alpha_iy_ib )\\ &=\frac{\partial}{\partial b} (-\sum_{i=1}^{m}\alpha_iy_ib )\\ &=\frac{\partial}{\partial b} (-b\sum_{i=1}^{m}\alpha_iy_i )\\ &=-\sum_{i=1}^{m}\alpha_iy_i \end{align} \]

通过这一波求偏导我们得到：

\[w=\sum_{i=1}^{m}\alpha_iy_i x_i\ \;,\ \,0=\sum_{i=1}^{m}\alpha_iy_i \]

将其带入 \(\mathcal{L}(x,\alpha,\beta)\) 即可得到最小值：

\[\begin{align} \min\limits_{w,b} \mathcal{L}(w,b,\alpha) &= {\frac {1} {2}} {||w||}^2+\sum_{i=1}^{m}\alpha_i[1-y_i(w^Tx_i+b)]\\ &=\frac{1}{2}w^Tw+\sum_{i=1}^{m}\alpha_i -w^T(\sum_{i=1}^{m}\alpha_i y_i x_i)-b(\sum_{i=1}^{m} \alpha_i y_i)\\ &=\frac{1}{2}w^Tw+\sum_{i=1}^{m}\alpha_i -w^Tw-b\cdot0\\ &=\sum_{i=1}^{m}\alpha_i-\frac{1}{2}(\sum_{i=1}^{m}\alpha_iy_i x_i)^T(\sum_{i=1}^{m}\alpha_iy_i x_i)\\ &=\sum_{i=1}^{m}\alpha_i-\frac{1}{2}(\sum_{i=1}^{m}\alpha_iy_i x_i^T)(\sum_{j=1}^{m}\alpha_jy_j x_j)\\ &=\sum_{i=1}^{m}\alpha_i-\frac{1}{2} [\sum_{i=1}^{m}\alpha_iy_i x_i^T(\sum_{j=1}^{m}\alpha_jy_j x_j) ] \\ &=\sum_{i=1}^{m}\alpha_i-\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i \alpha_j y_iy_jx_i^Tx_j \end{align} \]

对于条件②~⑤，SVM不存在等式约束，其余的条件对应为

\[\begin{cases}\alpha_i\ge0\;;\\ 1-y_i(w^Tx_i+b)\le0\;;\\ \alpha_i[1-y_i(w^Tx_i+b)]=0\;;\end{cases} \]

前两个式子是原始约束条件，而第三个式子就是之前在2.2.1中提到的“结论*”，当时为什么说它是一个重要结论呢，因为它触及到了SVM的核心，请看：

当 \(\alpha_i=0\) 时，则在目标函数的求和项中 \(\alpha_iy_i x_i=0\)，表示此 \(\alpha_i\) 对应的向量不会对超平面的确定有任何影响；

当 \(\alpha_i>0\) 时，则必有 \(y_i(w^Tx_i+b)=1\),表示此 \(\alpha_i\) 对应的向量在支撑超平面上(图2中虚线位置)，即支持向量；

这表明，划分超平面的确立只与支持向量有关。同时，如果我们要找出支持向量，只需找到非零 \(\alpha_i\) 对应的向量即可。所以说，此式揭示了 \(\alpha\) 的物理意义，是深入了解 SVM 的关键。

至此，我们得到了 SVM 的对偶形式：

\[\max_\alpha \ \sum_{i=1}^{m}\alpha_i-\frac{1} {2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i \alpha_j y_iy_jx_i^Tx_j\quad\;\;\;\;\mathrm{s.t.}\;\sum_{i=1}^{m}\alpha_iy_i=0\,,\,\alpha_i\ge0\,,\,i=1,2,...,m \]

接下来的问题是如何求解 \(\alpha\) 呢？

三、求解的方法

3.1 SMO算法基本思路

我们可以看到，在对偶问题中存在 \(m\) 个参数 \(\alpha\)，很难直接求得最优解。所以我们考虑使用迭代的方法每次只优化有限个参数。但由于 \(\begin{array} \,\sum_{i=1}^{m}\alpha_iy_i=0\end{array}\) 的限制，我们不能单独对某个参数更新，所以我们每次选取两个更新变量 \(\alpha_i\) 和 \(\alpha_j\)，而固定其余参数，通过反复的迭代求解对偶问题

SMO算法之所以高效，就是因为固定其余参数后仅优化两个参数的过程可以做到很高效，但为了减少迭代次数，每次选取哪两个参数还是有讲究的。我们知道，只要 \(\alpha_i\) 和 \(\alpha_j\) 中有一个不满足KKT条件，目标函数就会在迭代后减小。直观来看，KKT条件违背的程度越大，则更新变量后可能导致的目标函数值减幅越大，所以我们首先选取一个违背KKT条件程度最大的变量。第二个变量应该选择一个使目标函数值减小最快的变量，但由于比较各变量对目标函数值的减幅过于复杂，所以SMO采用了一个启发式(指根据经验或直观想法设计的算法，每一步不一定最优但节省资源)：使选取的两变量所对应的样本点间隔最大。因为我们直观上可以认为，比起对两个相似的变量进行更新，对两个有很大差别的变量进行更新会带给目标函数值更大的变化

思路：

①每次迭代过程仅优化两个参数，存在闭式解;(即任意参数都必能求得优化后的值，具体过程中可得证)

②启发式寻找每次要优化的两个参数，有效减少迭代次数；

方法：

①设置 \(\alpha\) 列表，并设其初始值为0；(每个数据点都对应一个 \(\alpha_i\))

②选取两个待优化变量;(为了便于讲解，这里将其记为 \(\alpha_1\) 和 \(\alpha_2\))

③求解两个变量的最优解 \(\alpha_1^*\) 和 \(\alpha_2^*\) ，并更新至 \(\alpha\) 列表中;

④检查更新后的 \(\alpha\) 列表是否在某个精度范围内满足KKT条件，若不满足则返回②；(这里考虑到了计算机存在浮点数的误差)

3.2 SMO算法基本实现

我们现在的问题为：

\[\max_\alpha \ \sum_{i=1}^{m}\alpha_i-\frac{1} {2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i \alpha_j y_iy_jx_i^Tx_j\quad\ \ \,\;\mathrm{s.t.}\;\sum_{i=1}^{m}\alpha_iy_i=0\,,\,\alpha_i\ge0\,,\,i=1,2,...,m \]

当选定两个待优化变量 \(\alpha_1\) 和 \(\alpha_2\)，我们将目标函数展开，去掉无关项并更新约束条件：

\[\begin{align} \max_{\alpha_1,\alpha_2} W(\alpha_1,\alpha_2)&=(\alpha_1+\alpha_2+\color{Green} {\sum_{i=3}^{m}\alpha_i})-\frac{1}{2}K_{11}\alpha_1^2-\frac{1}{2}K_{22}\alpha_2^2\\&\quad\; -y_1y_2K_{12}\alpha_1 \alpha_2-y_1\alpha_1 \sum_{i=3}^{m}y_i\alpha_iK_{i1}-y_2\alpha_2 \sum_{i=3}^{m}y_i\alpha_iK_{i2}\\ &=(\alpha_1+\alpha_2)-\frac{1} {2}K_{11}\alpha_1^2-\frac{1}{2}K_{22}\alpha_2^2-y_1y_2K_{12}\alpha_1 \alpha_2\\&\quad\; -y_1\alpha_1 \sum_{i=3}^{m}y_i\alpha_iK_{i1}-y_2\alpha_2 \sum_{i=3}^{m}y_i\alpha_iK_{i2} \end{align} \]

\[\begin{array} \mathrm{s.t.}\ &\alpha_1y_1+\alpha_2y_2=-\sum_{i=3}^{m}y_i\alpha_i=\xi\,,\\ &\alpha_i\ge0\;,\,i=1,2,...,m \end{array} \]

其中 \(K_{ij}\) 代表 \(\alpha_i^T\alpha_j\)，是核函数(Kernel Function)，目前只用知道它等价于变量在特征空间的内积即可，后面的章节会对它具体讲解

我们现已将问题转化成一个二元二次问题，而利用约束条件我们可将其再次转化为一元二次问题，最后通过比较最值点和可行域之间的关系即可获得可行域中的最值

记 \(\quad\, v_i=\sum_{j=3}^{m}y_j\alpha_jK_{ij}=f(x_i)-\sum_{j=1}^{2}y_j\alpha_jK_{ij}-b\;,\,i=1,2\)

有： \(\;\begin{align}W(\alpha_1,\alpha_2)= & \frac{1}{2}K_{11}\alpha_1^2+\frac{1}{2}K_{22} \alpha_2^2+y_1y_2K_{12}\alpha_1 \alpha_2\\ &-(\alpha_1+\alpha_2)+y_1v_1\alpha_1+y_2v_2\alpha_2 \end{align}\)

回代 \(\ \,\alpha_1y_1+\alpha_2y_2=-\sum_{i=3}^{m}y_i\alpha_i=\xi\;\Longleftrightarrow\ \alpha_1=(\xi -y_2\alpha_2)y_1\)

得: \(\qquad \begin{align} W(\alpha_2)=&\frac{1} {2}K_{11}(\xi-\alpha_2y_2)^2+\frac{1}{2}K_{22}\alpha_2^2+y_2K_{12}(\xi-\alpha_2y_2)\alpha_2\\ &-(\xi-\alpha_2y_2)y_1-\alpha_2+v_1(\xi-\alpha_2y_2)+y_2v_2\alpha_2 \end{align}\)

对 \(\alpha_2\) 求偏导：

\[\qquad\begin{align}\frac{\partial W}{\partial \alpha_2}=&K_{11}\alpha_2+K_{22}\alpha_2-2K_{12}\alpha_2-K_{11}\xi y_2\\ &+K_{12}\xi y_2+y_1y_2-1-v_1y_2+y_2v_2 =0 \end{align}\\ \Big\Updownarrow\\ (K_{11}+K_{22}-2K_{12})\alpha_2=y_2( y_2-y_1+\xi K_{11}-\xi K_{12}+v_1-v_2 )\\ \]

\[\begin{align} &=y_2\Big[y_2-y_1+\xi K_{11}-\xi K_{12}+\big(f(x_1)-\sum_{j=1}^{2}y_j\alpha_jK_{1j}-b \big) \\ &-\big( f(x_2)-\sum_{j=1}^{2}y_j\alpha_jK_{2j}-b \big) \Big] \end{align} \]

将 \(\xi =\alpha_1^{old}y_1+\alpha_2^{old}y_2\) 代入，并设 \(E_i=f(x_i)-y_i\)，有：

\[\begin{align} & \;(K_{11}+K_{22}-2K_{12}) \alpha_2^{new,unc}\\ &=y_2\Big[(K_{11}+K_{22}-2K_{12})\alpha_2^{old}y_2+y_2-y_1+g(x_1)-g(x_2) \Big]\\ &=(K_{11}+K_{22}-2K_{12})\alpha_2^{old}+y_2(E_1-E_2) \end{align} \]

这里的 \(\alpha_2^{new,unc}\) 表示这个 \(\alpha_2^{new}\) 还没有与可行域进行比较(unclear)，不一定是最终的 \(\alpha_2^{new}\)

记 \(\eta=K_{11}+K_{22}-2K_{12}\),有：

\[\alpha_2^{new,unc}=\alpha_2^{old}+\frac{y_2(E_1-E_2)} {\eta} \]

接下来，我们要将可行域内的得到的最优解与可行域的边界进行比较

\(\alpha\) 的可行域：

\[L\ \le \ \alpha^{new}\le H \\ \alpha_1y_1+\alpha_2y_2=\xi \]

根据 \(y_1,y_2\) 的符号关系分类有：

\[\begin{cases} L=\max(0\ ,\, \alpha_2^{old}-\alpha_1^{old}) ,\ H=+\infty, &\mathrm{if}\ \ \, y_1=-y_2 \\ L=0 \ ,\ H=+\infty, \quad &\mathrm{if}\ \ \, y_1=\ \ y_2 \end{cases} \]

可得：

\[\alpha_2^{new} =\begin{cases} H\ , \quad\quad \quad &\alpha_2^{new,unc}\ge H\\ \alpha_2^{new,unc} ,&L\le \alpha_2^{new,unc} \le H\\ L\ ,& \alpha_2^{new,unc}\le H \end{cases} \]

而根据

\[\alpha_1^{new}y_1+\alpha_2^{new}y_2=\alpha_1^{old}y_1+\alpha_2^{old}y_2 \]

有：

\[\alpha_1^{new}=\alpha_1^{old}+y_1y_2(\alpha_2^{old}-\alpha_2^{new}) \]

至此我们已经得到更新 \(\alpha\) 参数的方法，下面说说两个待优化变量如何选取

思想：选取的两个变量所对应的样本之间的间隔最大，且违反 KKT 条件的程度要大，以期待它们带来的差异能给目标函数值更大的变化

方法：

①选取第一个变量，便利训练样本点，检验它们是否满足 KKT 条件(在一定精度范围内)，选择任一违反 KKT 条件的变量

②选取第二个变量,在选择了第一个变量的基础上，我们希望选取的第二个变量能够带来,足够的变化量；\(\alpha_2\) 的更新依赖 \(|E_1-E_2|\)，故当 \(E_1\ge0\) 时，我们选取最小的 \(E_2\)，反之选取最小的 \(E_2\)；若更新量不够，则选择 \(\alpha_2\neq0\) 的点；若更新量仍不够，则遍历剩余的点；若更新量还不够，则重新选择 \(\alpha_1\)，并按照上述逻辑再次选取 \(\alpha_2\)；

3.3 算法总结

当我们优化更新完所有的 \(\alpha_i\) 参数，便可以得出最优划分超平面的解了

由之前KKT条件①求偏导那一步可得：

\[w^*=\sum_{i=1}^{m}\alpha_iy_ix_i \]

由唯一性可知，\(b^*\) 为一确定值，我们选出任一支持向量，其满足：

\[y_i(w^{*T}x_j+b^*)-1=0\\ \Updownarrow\\ y_i^2(w^{*T}x_j+b^*)-y_i=0 \]

得出:

\[b^*=y_i-w^{*T}x_j=y_j-\sum_{i=1}^{m}\alpha_iy_i(x_i^Tx_j) \]

现实任务中我们采取一种更鲁棒的做法：使用所有支持向量求解再取平均值，得出：

\[\begin{align}&b^*=\frac{1}{|S|}\sum_{s\in S}\Big(y_s-\sum_{i\in S}\alpha_iy_ix_i^Tx_s\Big),\\&\mathcal{s.t.} \quad S= \{ { i\ |\ \alpha_i>0,i=1,2,...,m}\}\end{align} \]

最后，我们来做一下总结：

线性可分支持向量机
输入：线性可分训练数据集 \(T=\{(x_1,y_1),(x_2,y_2),...,(x_m,y_m) \}\)

其中 \(x_i\in R^n,y_i\in\{-1,1 \},i=1,2,...,m\)

输出：最优划分超平面和分类决策函数

构造并求解约束最优化问题：

\[\max_\alpha \ \sum_{i=1}^{m}\alpha_i-\frac{1} {2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i \alpha_j y_iy_jx_i^Tx_j\quad\ \\\mathrm{s.t.}\;\sum_{i=1}^{m}\alpha_iy_i=0\,,\,\alpha_i\ge0\,,\,i=1,2,...,m \]

求得最优解 \(\alpha^*=(\alpha_1^*,\alpha_2^*,...,\alpha_m^*)^T\)，并计算

\[\begin{array} \,w^*= &\sum_{i=1}^{m}\alpha_i^*y_ix_i,\\ \,b^*\,=&y_j-\sum_{i=1}^{m}\alpha_i^*y_i(x_i^Tx_j)\end{array} \]

由此得到划分超平面：

\[w^{*T}x+b^*=0 \]

分类决策函数：

\[f(x)=\mathrm{sign}(w^{*T}x+b^*) \]

四、软间隔SVM及核方法

4.1 软间隔SVM

在前面的讨论中，我们假设了样本点是线性可分的，而现实中的样本往往很难达到完全线性可分。退一步说，即使可以达到完全线性可分，我们找到的超平面也不一定是最好的，很可能会因为钻了一两个数据点的牛角尖而出现过拟合的现象。缓解该问题的办法是允许支持向量机在少部分点上“出错”，为此我们引入“软间隔(Soft Margin)”的概念

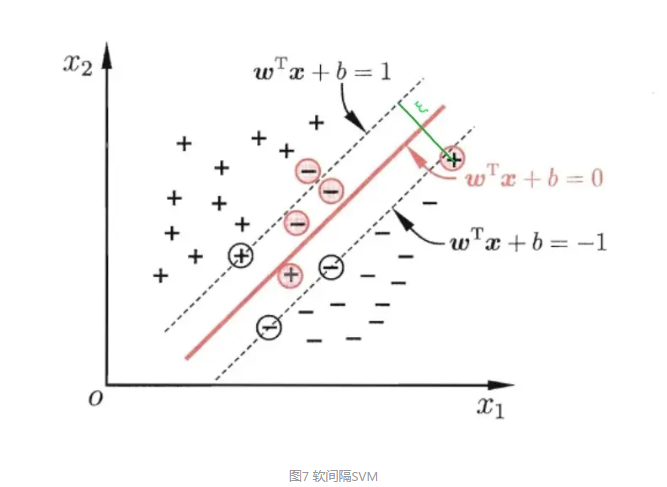
如图7所示，我们允许部分样本点不满足 \(1-y_i(w^Tx_i+b)\le0\) 的条件而越过相邻的支撑超平面那么接下来我们需要考虑两个方面的指标：一是错误样本点越界的程度，二是错误样本点的数量。所以我们引入两个新的变量：表示错误样本点超出支撑超平面的距离 \(\xi_i\) ，对错误样本点的惩罚程度 \(C\) (惩罚程度越高产生的数量自然越少，由此来控制数量和距离)

增加软间隔后，我们的优化目标变为：

\[\min_w\ \ \ \frac{1}{2}||w||^2+C\sum_{i=1}^m\xi_i\\ \begin{align}\mathrm{s.t.}\ \ \,& 1-y_i(w^Tx_i+b)-\xi_i\le0,\\ &\xi_i\ge0 \,,\;i=1,2,...,m \end{align} \]

其中 \(C\) 是一个大于 \(0\) 的常数，其值越大表示对错误的容忍性越小。可以想象当 \(C\) 趋于无穷大时，\(\xi_i\) 必然趋于无穷小，即回到了线性 SVM

按照处理线性SVM 的套路，我们来优化该问题：

①构造拉格朗日函数

\[\begin{align}L(w,b,\alpha,\xi,\mu)= &\frac{1}{2}||w||^2+C\sum_{i=1}^m\xi_i-\sum_{i=1}^m\mu_i\xi_i\\ &+\sum_{i=1}^m\alpha_i\big [ 1-\xi_i-y_i(w^T+b)\big] \end{align} \]

其中， \(\alpha_i\ge0,\mu_i\ge0\) 是拉格朗日乘子

②根据强对偶性，转化问题为

\[\max_{\lambda,\mu}\min_{w,b,\xi}L(w,b,\xi,\alpha,\mu) \]

③对极小化问题利用 KKT 条件，令 L 对 \(w,b,\xi_i\) 的偏导为 0 可得

\[w=\sum_{i=1}^{m}\alpha_iy_ix_i\ ,\ 0=\sum_{i=1}^{m}\alpha_iy_i\ ,\ C=\alpha_i+\mu_i \]

代入拉格朗日函数可得

\[\max_\alpha \ \sum_{i=1}^{m}\alpha_i-\frac{1} {2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i \alpha_j y_iy_jx_i^Tx_j\\ \quad\ \ \,\;\mathrm{s.t.}\;\;\sum_{i=1}^{m}\alpha_iy_i=0\,,\,0\le\alpha_i\le C\,,\,i=1,2,...,m \]

软间隔 SVM 的 KKT 条件还有

\[\begin{cases}\alpha_i\ge0\ ,\ \mu_i\ge 0\;;\\ 1-y_i(w^Tx_i+b)-\xi_i\le0\;;\\ \alpha_i[1-y_i(w^Tx_i+b)-\xi_i]=0\;;\\ \xi_i\ge0\ ,\ \mu_i\xi_i=0\;;\end{cases} \]

④利用 SMO 算法解得拉格朗日乘子 \(\alpha^*\)，得出

\[\begin{align}& w^*=\sum_{i=1}^{m}\alpha_iy_ix_i\;,\\ &b^*=\frac{1}{|S|}\sum_{s\in S}\Big(y_s-\sum_{i\in S}\alpha_iy_ix_i^Tx_s\Big),\\&\mathcal{s.t.} \quad S= \{ { i\ |\ \alpha_i>0,i=1,2,...,m} \}\end{align} \]

最终得到最优划分超平面 \(w^{*T}x+b^*=0\)；
同样的， \(\alpha_i\ge0\) 对应的数据点为支持向量，这就包括了越界的那些错误点，它们也是影响超平面的确立的。

4.2 核函数

前面讨论了线性 SVM 以及软间隔 SVM，它们可应用于样本全部或大部分线性可分的情况，那么如果样本呈现为图1中左边的情况呢？

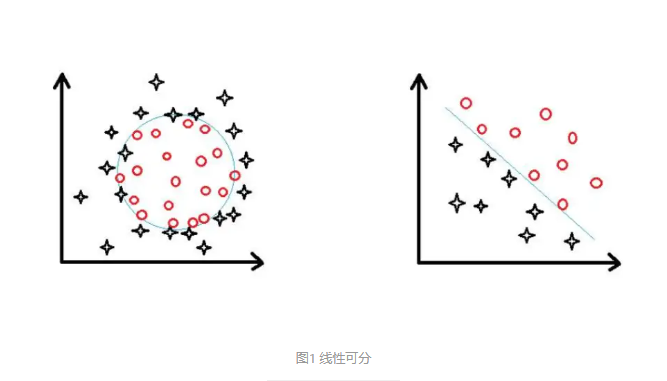
这时候我们采取的方法是，将二维线性不可分的样本映射到高维空间中去，并使其可分。就比如我们不能从年龄，体重来区分小猪和小羊，但是我们增加一个维度角的数量就可以达到区分的目的，这种方法称为核技巧(请点开看这个生动的案例)。《机器学习》中也提到了一个简明的例子，“异或”问题

对于在有限维度向量空间中线性不可分的样本，我们将其映射到更高维度的向量空间里，再通过间隔最大化的方式，学习得到支持向量机，就是非线性 SVM。我们用 \(x\) 表示原来的样本点，用 \(\phi(x)\) 表示映射到新的特征空间后得到的点。那么分割超平面可以表示为：

\[f(x)=w\phi(x)+b \]

通过同样的套路，我们也可以求得非线性 SVM 的对偶问题：

\[\max_\alpha \ \sum_{i=1}^{m}\alpha_i-\frac{1} {2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i \alpha_j y_iy_j\phi(x_i)^T\phi(x_j)\\ \mathrm{s.t.}\;\;\sum_{i=1}^{m}\alpha_iy_i=0\,,\,\alpha_i\ge0 \,,\,i=1,2,...,m \quad \]

但这时我们发现一个问题，就是该如何去求解高维特征空间中的内积呢？为了避开这个障碍，我们设想有这么一个函数：

\[k(x_i,x_j)=\langle\phi(x_i),\phi(x_j)\rangle=\phi(x_i)^T\phi(x_j) \]

即使得 \(x_i\) 与 \(x_j\) 在高维特征空间的内积就等于它们在原始样本空间中通过 \(k(\cdot\,,\,\cdot)\) 计算得到的结果。如果有这样的函数存在，我们将其带入对偶问题中即可求得最优划分超平面为：

\[\begin{align} f(x)&=w^T\phi(x)+b\\ &=\sum_{i=1}^{m}\alpha_i y_i \phi(x_i)^T\phi(x)+b\\ &=\sum_{i=1}^{m}\alpha_i y_i k(x,x_i)+b \end{align} \]

这里的 \(k(\cdot\,,\,\cdot)\) 就是“核函数”(kernel function)

那么合适的核函数是否一定存在呢？什么样的函数能做核函数呢？有哪些常用的核函数以及如何选取呢？某乎上有很多精彩的回答，感兴趣的同学可以去翻一翻，我这里就略过了

五、SVM 的优缺点及应用

5.1 SVM 的优缺点

优点：

有严格的数学理论支持，可解释性强，不依靠统计方法，从而简化了通常的分类和回归问题
能找出对任务至关重要的关键样本(即支持向量)
采用核技巧之后，可以处理非线性分类/回归任务
最终决策函数只由少数的支持向量所确定，计算的复杂性取决于支持向量的数目，而不是样本空间的维数，这在某种意义上避免了“维数灾难”

缺点：

训练时间长。当采用SMO算法时，由于每次都需要挑选一对参数，因此时间复杂度为，其中 N 为训练样本的数量
当采用核技巧时，如果需要存储核矩阵，则空间复杂度为
模型预测时，预测时间与支持向量的个数成正比。当支持向量的数量较大时，预测计算复杂度较高

因此支持向量机目前只适合小批量样本的任务，无法适应百万甚至上亿样本的任务

5.2 SVM 的应用

SVM 技术在解决小样本、非线性及高维度的模式识别问题中表现出明显的优势。在许多领域，如文本分类、图像识别、生物信息学等领域中得到了成功的应用

Scikit-learn 库中带有封装好的 SVM，我们可以方便地应用 SVM

六、回顾

本文详细介绍了支持向量机的算法原理，全篇重要知识点如下：