计算机图形学六：光线追踪-Ray Tracing

阴影映射（Shadow Mapping）

其实这应该是属于纹理映射这一块的知识，但是闫老师当时没说，知道几何的最后一块才说，因为这又与光线追踪有关，所以我就把它记录于此。

前面我们说过着色，它仅仅考虑着色点与光照这两者，忽略了其他物体甚至自身对于着色点的遮挡关系，这显然是不对的。光源被遮挡，必然会产生阴影，而光栅化并不能很好的表示这种阴影。而阴影映射可以较好的解决这个问题。

再来一遍废话，为什么会有阴影？

因为光源照射不到，更具体点，摄像机能看到的地方，光源“看”不见。

而这正是启发阴影贴图这种做法的动机，接下来我们便来看看详细过程是怎么样的。

第一步，把光源当做一个摄像机让它去看，去渲染整个场景一遍从而得到从光源视角的深度Buffer，记为 $d_{map}$。它被记录在 shadow map中。如图中就记录了四个点的深度

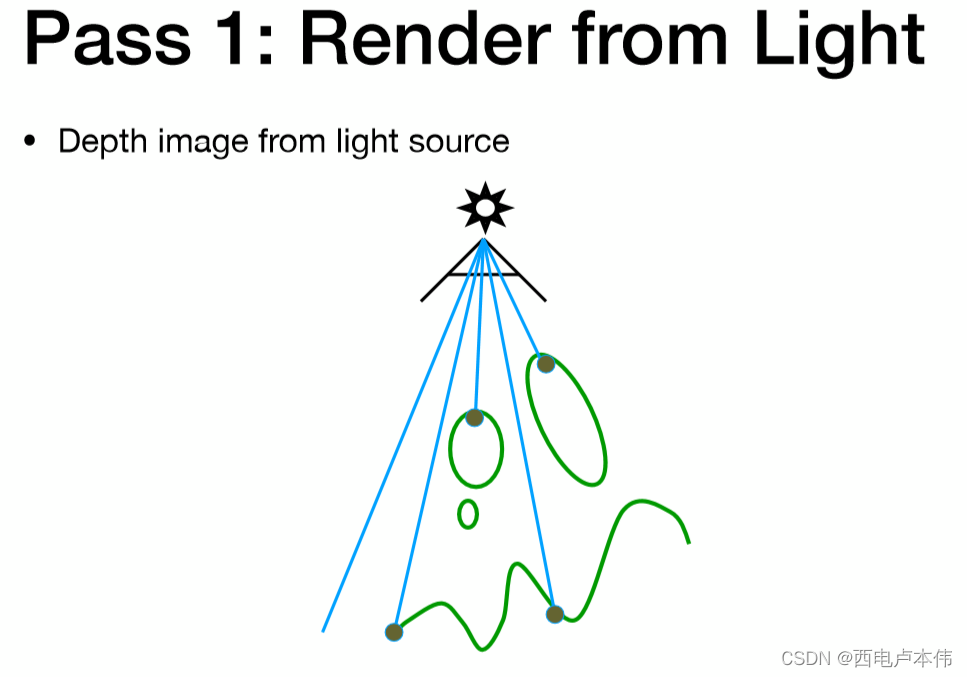第二步，从设定好的摄像机位置去真正的渲染场景得到摄像机视角的深度Buffer，记为 $d$

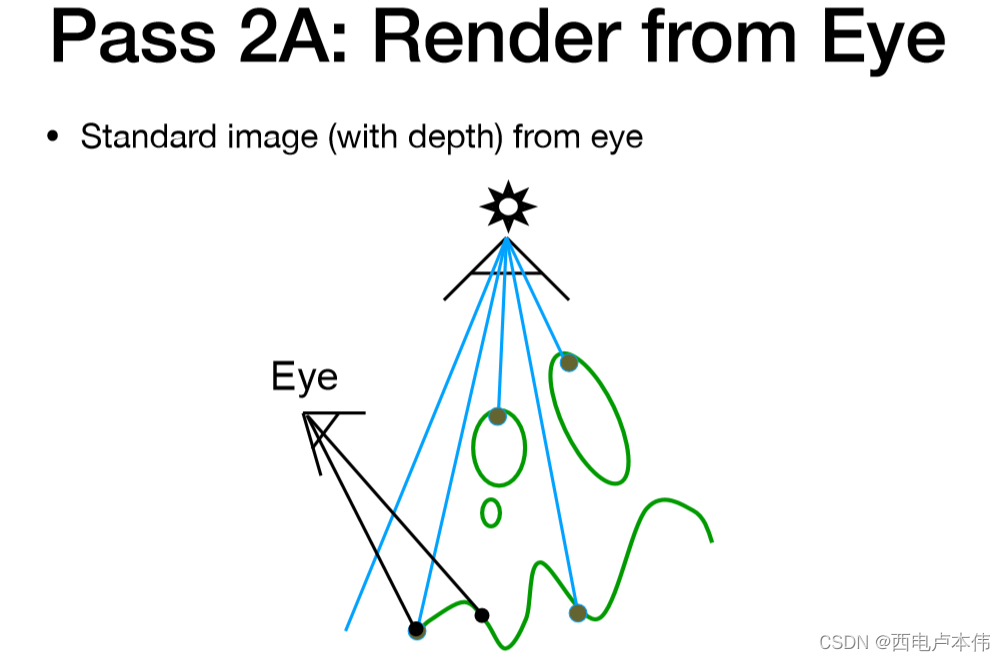
第三步，将所有摄像机视角可见点，利用光源视角下的那一套投影矩阵，重新投影回光源，找到与shadow map上对应的 $d_{map}$

如果该点的 $d_{map}$ 与 $d$ 相等，则说明此点可被光源与摄像机共同看见，因此不在阴影中，如下图橘色线条这种情况：

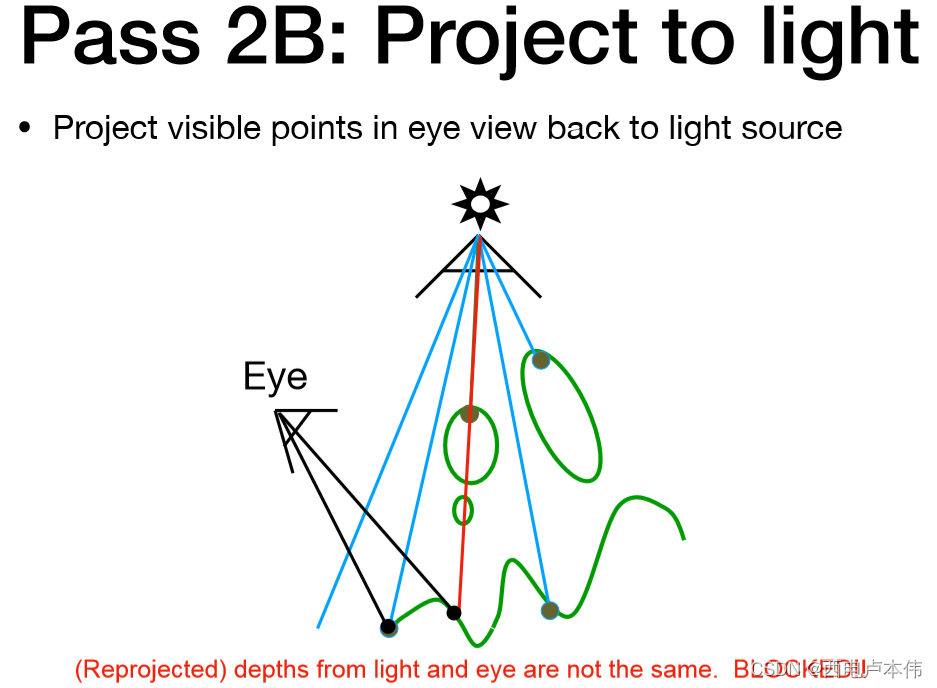
如果该点的 $d_{map}$ 小于 $d$ ，则说明此点不可被光源看见，但摄像机看得见，即该点前方有物体遮挡，因此在阴影中，如下图红色线这种情况：

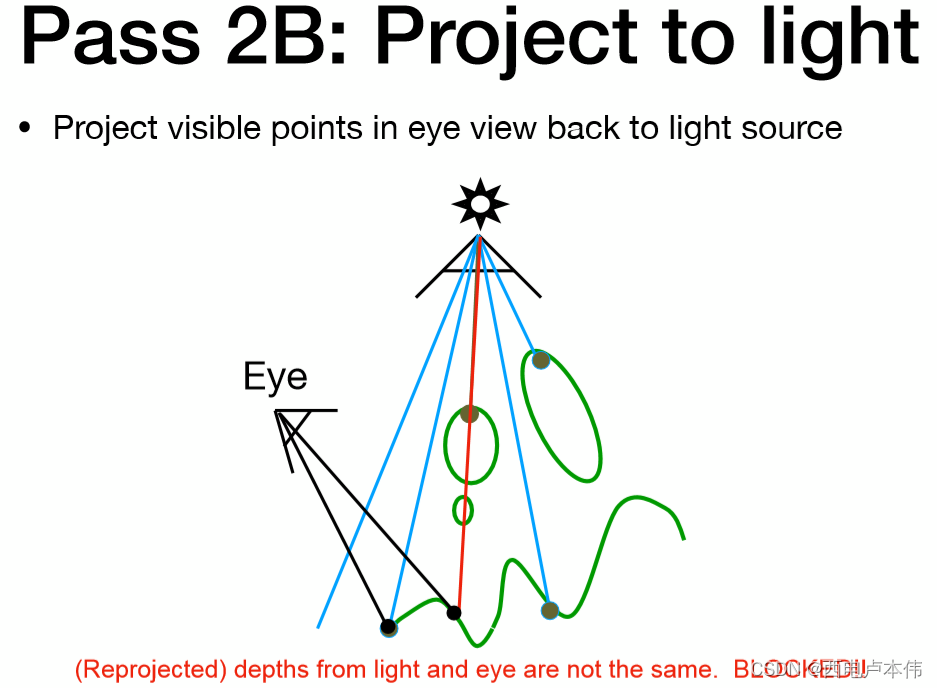
如此便能确定每个可见像素点是否在阴影之中了，如果在阴影之中就不去计算Blinn-Phong中的镜面反射项与漫反射项。效果如下图：

对应可视化的shadow map如下，距离光源越近代表深度越小，所以颜色越黑（同Z-Buffer），反之亦然：

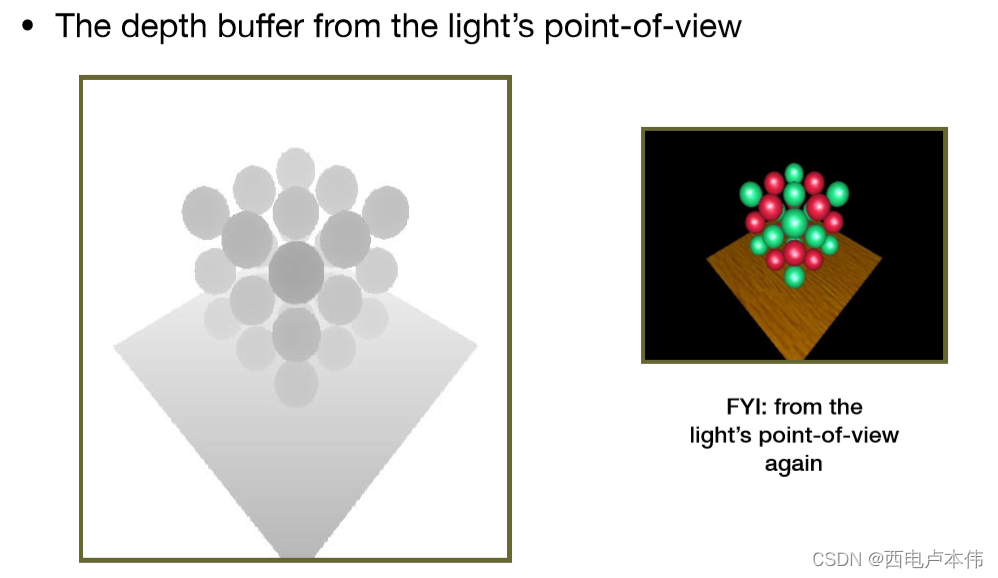
阴影映射这种方式确实可以较好表示阴影，但它仍有限制：只适用于点光源，只能描述硬阴影。

什么是硬阴影？什么是软阴影？软硬阴影示意如下，上方棱角分明为硬阴影，下方为软阴影：

可见现实生活中，软阴影更符合认知，在阴影与没有阴影之间有一个渐变的过度，更加自然。产生软阴影是因为光源具有体积，导致，有的地方完全看不到光源（本影, Umbra）， 有的地方能看到一部分光源（半影，Penumbra）。所以阴影的边缘会有过渡的情况，从而产生软阴影，就像上图中太阳与地球的示意一样（全日食与半日食）。

Whitted-Style 光线追踪

首先要清楚的是，我们为什么需要光线追踪？

在光栅化着色这一章节中，我们介绍了Blinn-Phong反射模型，但这个模型的 bug 之处也是十分明显的，它只考虑了光源到物体的直接光照，其它的间接光照一概不考虑，物体之前的遮挡关系也不考虑。这显然是不对的，例如：

如上图中房屋顶部的所接受到的光可不仅仅是Blinn-Phong模型考虑的直接光源，还有可能是来自窗外的光源照射到地板，再发生反射照射到了房屋顶部，而这部分光是局部光照模型没有考虑到的，而光线追踪正是为了解决这种问题所提出的一种全局光照模型。

原理

光线追踪，顾名思义，核心是光线。首先对光线做一些假设：

1. 光线一定沿着直线传播
2. 光线之间无法碰撞
3. 光线路径可逆，即从A发出的到B的光线，一定也可以从B发出到A（中途可发生反射和折射）

人为什么能看到不同的物体？是因为从物体表面上有光进入了人眼。那由上述的假设是不是也可理解为人眼发出了很多感知光线碰撞到了物体，所以可以看见呢？在古代可还真就有不少人这么想：

当然现代物理知识已经告诉我们这种观点是错误的，但是并不妨碍从中获取一些灵感：光路可逆，所有进入到人眼的光，都可从人眼发出光按照原路反方向返回，那么利用这种模拟从人眼发射光线的方法不就可以还原出所有的光路了呢？这就是光线追踪的核心想法，反其道而行之。

第一步：Ray Casting

从人眼（摄像机）向近投影平面上的每一个像素点发射一条光线，判断与场景物体的交点，示意图如下：

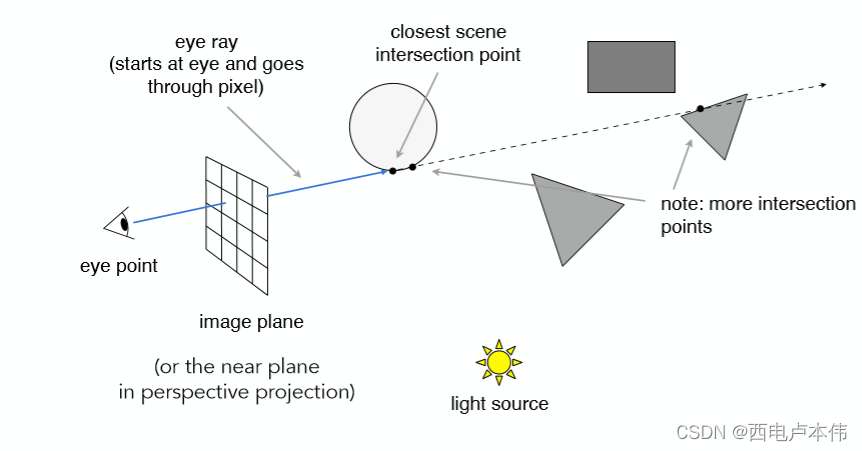
当然一条光线自然可能会与不止一个物体相交，但是考虑遮挡关系，只去找最近的交点。接着连接该交点和光源，只要判断这条连线之间是否有物体存在就可以知道该交点是否在阴影之中（原理同上述shadow mapping）：

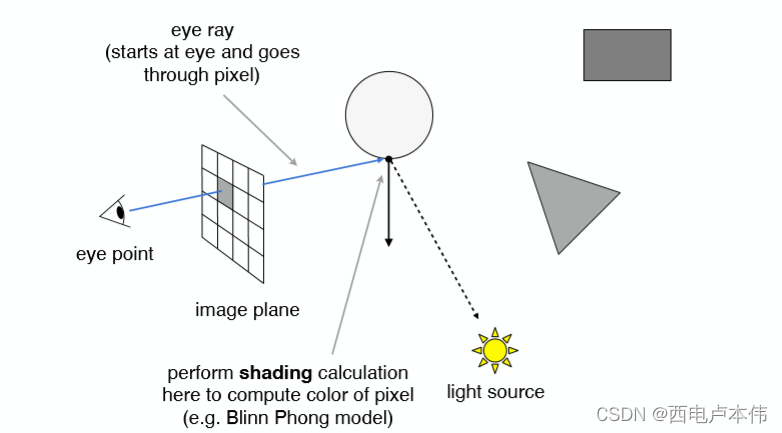
紧接着，自然可以利用Blinn-Phong模型对这个点进行局部光照模型计算，对该像素进行着色，那么遍历所有近投影平面上的像素就能得到一张完整的图像。到目前位置，这与Blinn-Phong模型的思路如出一辙。

第二步 Recursive (Whitted-Style) Ray Tracing

考虑第一步中所做的Ray Casting，该条光线第一个与圆球物体相交，假设该圆球是一个玻璃球，那么便会发生镜面反射，如图：

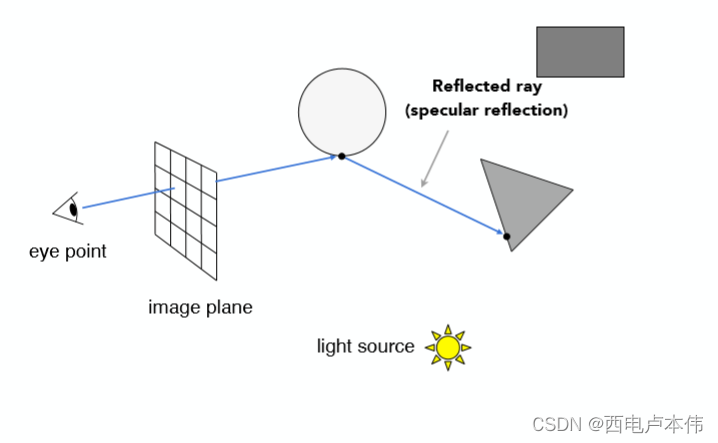
当然除了镜面反射之外，也存在折射，同时反射与折射出去的光线会可能与场景中的物体再次碰撞，发生第二次折射与反射：

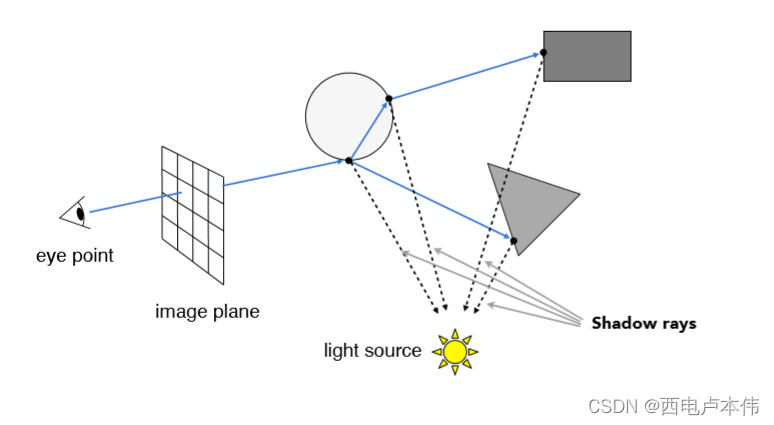
当然，还有其他“无数次的反射与折射”

从图中可以见到，不仅仅是与圆球相交的那一点可以贡献光到达眼睛，折射与反射之后再与物体相交的点也可以贡献光（光路可逆原理）。简而言之，除了直接从光源照射到圆球交点再沿着 eye rays（第一条发射的光线）到眼睛中，也可能存在这样一种情形，有光照射到其他物体，再沿着eye rays的反射或折射的光线方向传回人眼。

因此每一个着色点的颜色贡献来自这样种几类型 直接光照，反射方向间接光，折射方向间接光（如果有折射的话）

下一步将这些所有交点与光源连接，称这些线为shadow rays（因为可以用来检测阴影），计算这些所有点的局部光照模型的结果，将其按照光线能量权重累加，最终得到近投影平面上该像素点的颜色。这就是一个全局光照模型，因为不仅仅考虑了直接光源的贡献，还考虑各种折射与反射光线的贡献。

以上就是光线追踪的整个过程，还有额外几点要注意的：

1. 整体过程是一个递归（光无限的折射反射）的过程，因此需要一定的递归终止条件，比如说允许的最大反射或折射次数为10。
2. 光线在每次反射和折射之后都有能量损耗的，由系数决定，因此越往后的折射和反射光贡献的能量越小。
3. 如果反射或折射光线没有碰撞到物体，一般直接返回一个背景色。

参考伪代码如下：

RayTracing (original_point, ray_direction, objects, depth){  //着色点，光线方向，物体，深度
	if(depth > maxDepth)
		return color(0,0,0);          //深度测试
	if(IsHitobject(original_point, ray_direction, objects)){     //如果光线与物体有交点
		hitPoint = GetHitPoint();     //找到交点
		normal = GetNormal();         //找到法线
        
		reflectionDirection = reflect(ray_direction,normal); //求得反射方向
		refractionDirection = refract(ray_direction,normal); //求得折射方向，如果没有折射，舍弃折射项
        
		local_ color = BlinnPhongShader(original_point,normal,light_position)   //着色
            
		return local color
			+ k1*RayTracing(hitPoint,reflectionDirection,objects,depth + 1);    //继续从该反射光线求反射折射
			+ k2*RayTracing(hitPoint,refractionDirection,objects,depth + 1);    //继续从该折射光线求反射折射
    }
	else
		return background color;
}

光线与物体求交

上述Whitted-Style模型中有一个重要的问题，我们如何得到光线与物体的交点呢？在讨论之前，我们先对光线进行一个定义。

光线的表示方法

将每一条光线想象成一条射线，那么每一条光线都会由起点及方向这两个属性所固定，如下图所示：

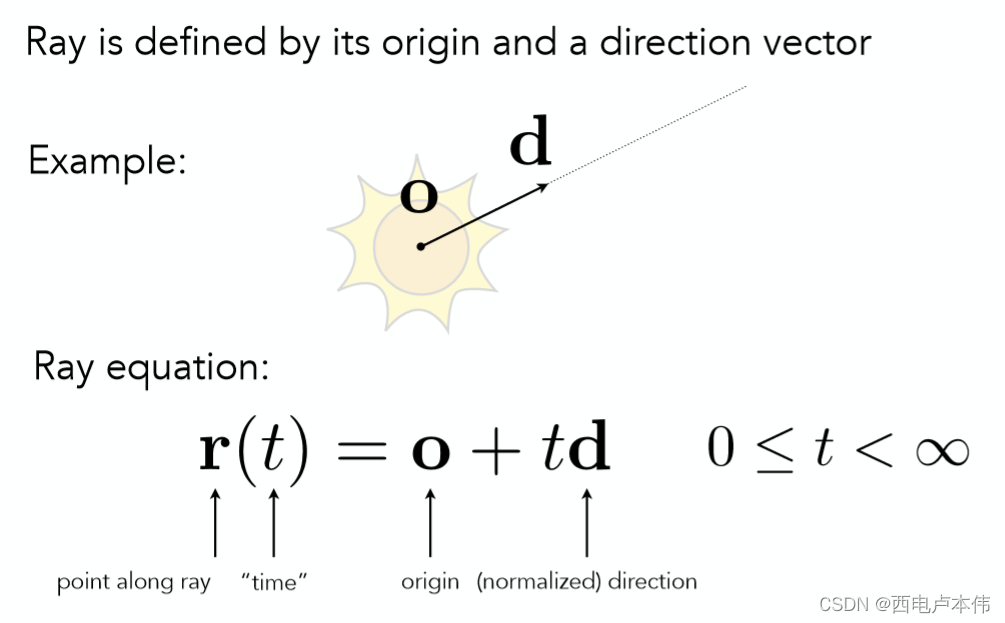
除了起点 $\mathbf{o}$ ，以及光线方向 $\mathbf{d}$ 之外，还额外定义了一个参数 $t$ 来表示光线行进的长度（ $t$ 当然是非负数，因为方向已定）。

光线与隐式曲面求交

首先计算光线与隐式曲面的交点的方法，以一个球体为例，二者表示方程如下：

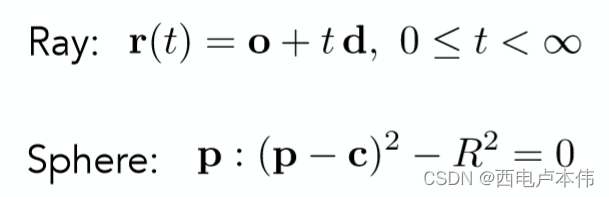
光线的表示方法在上节已经介绍过，对于一个球体来说，其表面上所有点 $\mathbf{p}$ , 到圆心 $\mathbf{c}$ 的距离是固定为 $R$ 的， 也就得到了上述的球的隐式曲面方程。那么对于一个光线会在什么时候与球相交呢？

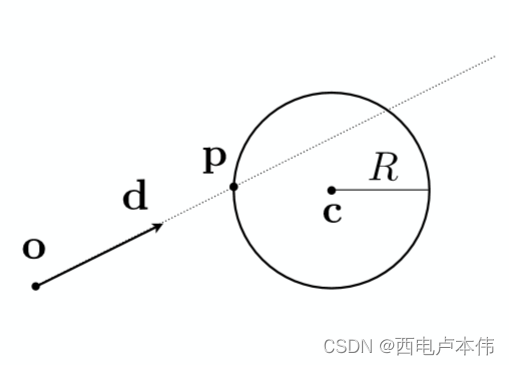
这个应该初中生都知道吧（嘻嘻），当然是在一个点既满足光线方程，又满足球体方程的时候，所以可以计算如下，把 $\mathbf{p}=\mathbf{o}+t\mathbf{d}$ 代入球体方程，利用一元二次方程的解法即可得到参数 $t$ 值：

同样的根据 $b^2-4ac$ 的正负关系，即可判断光线与球是一个交点还是两个交点又或是没有交点，这个应该初中生都知道吧（嘻嘻）。

虽然这里只举了对一个球的隐式曲面交点的计算，对于所有其他隐式曲面过程都是类似的，只要将光线方程代入求解 $t$ 即可：

光线与显示曲面求交

在几何中提到过，最常用的曲面表示形式，是通过定义各个多边形面的顶点以及顶点之间的连接关系得到许许多多的三角形面。因此如何判断一条光线与显示曲面的交点，其实也就是计算光线与三角形面的交点。进一步想，直接求光线是否与三角形有交点可能比较难，我们可以通过先求光线是否与该三角形所在平面有交点，再判断交点是否在三角形内来进行判断。对于任意一个平面，可以用如下图中的式子表达：

$\mathbf{N}$ 是平面的法线， ${\mathbf{p}}^{\prime }$ 是平面内的一点（这两个元素就可以确定一个平面了，想想看是不是这样）。 而 $ax+by+cz+d=0$ 是高数中对平面的一般化表示。那么到这里其实已经成功把对显示曲面的求交又转化为了类似隐式曲面求交的方法。

首先给出如何计算光线与平面交点的过程：

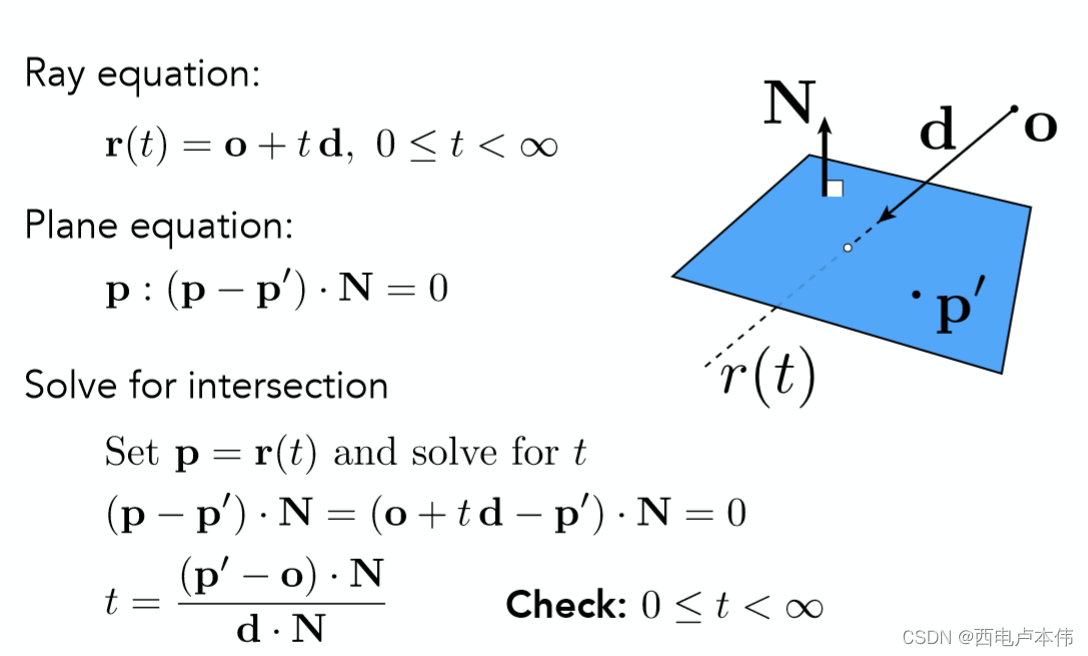
得到参数 $t$ 之后，自然可以计算出交点，如何判断交点是否在三角形内的问题以及多次讨论：可以用右手定则，也可以用重心坐标。但是这种方法略显繁琐，能不能一步就得到结果呢？利用重心坐标就可以：

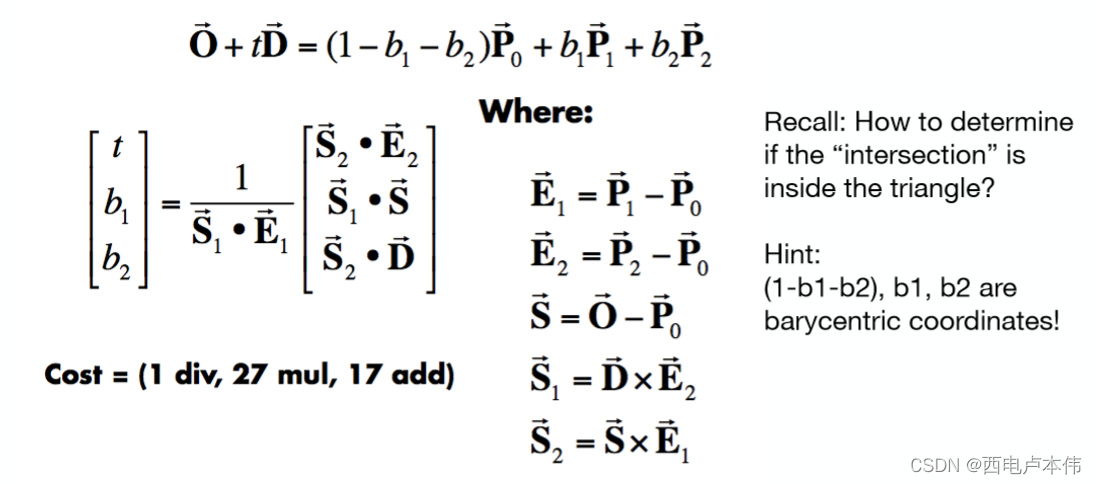
重心坐标可以表示位于三角形面内的任意一点，我们直接让它等于光线表达式，求解 $t,b_1,b_2$ 即可。如何求解多项式，线性代数中克莱姆法则可以解决（当然我已经忘了）…

至此，whited-style光线追踪的第一个小问题得以解决。相比与光栅化中所使用的的Blinn-Phong模型，光线追踪显著了提升了图像质量，但随之而来的问题是渲染速度过慢。因为在判断光线与场景交点的时候，需要去进行所有三角形面与光线的求交，而且这仅仅是对一个像素而言。那么总体来说光是进行光线与三角形的求交这样一个计算过程就一共要： 像素数量*三角形面数量*弹射次数 这么多次，如下图这样一个场景，一共就有10.7M的三角形面，你可以想象一共要多少次求交运算吗？

因此必须要寻求一些办法加速光线追踪的方法。

如何加速

轴对齐包围盒（Axis-Aligned Bounding Box）

AABB（Axis-Aligned Bounding Box）的提出是十分自然的，当有的光线显然不会与一个物体相交的时候，那么自然也没有必要去遍历该物体的所有三角形面，因此利用一个包围盒包住该物体，在与该物体的三角面计算求交之前先判断光线是否与包围盒相交，倘若连包围盒都与光线没有交点的话，那么显然不会与物体的三角面有交点。

而所谓AABB也是一种包围盒，也是由三对平面的交集构成，只不过AABB的任意一对平面都与 $x-axis，y-axis$ 或者 $z-axis$ 垂直，所以称之为轴对齐包围盒。如下图所示：

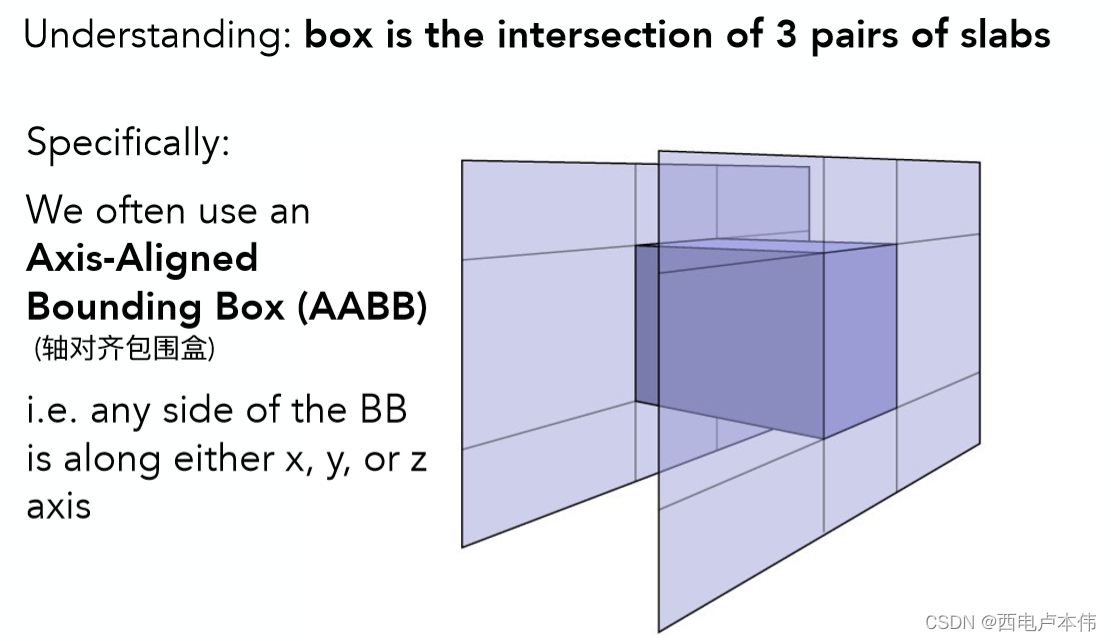
之所以这么设置的原因是为了方便进行光线与包围盒的求交运算。那么问题就转换成了如何求光线与包围盒的交点。

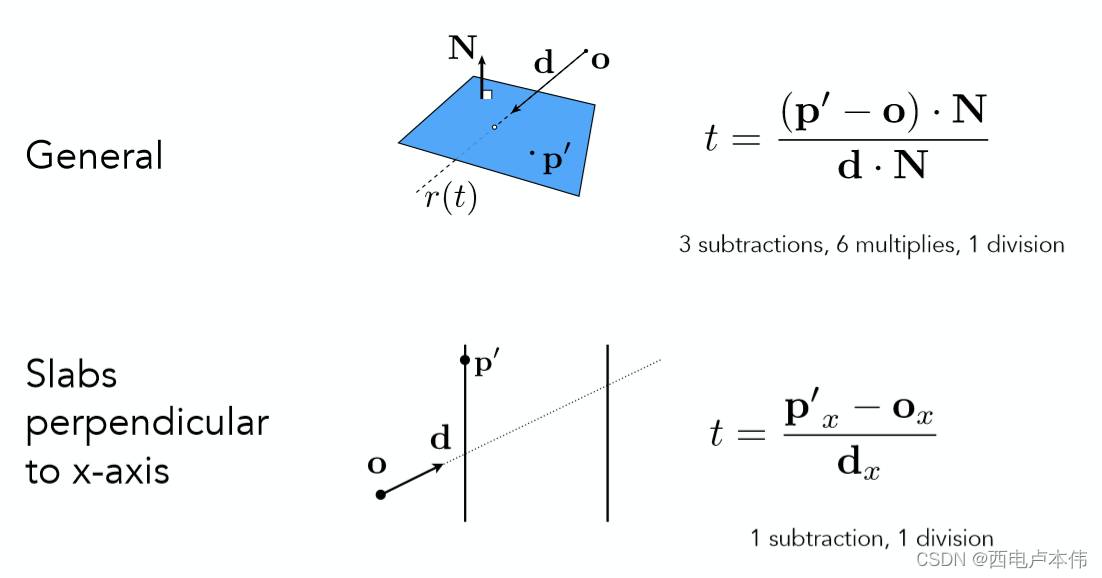
我们以2D的AABB为例，因此只有 $x，y$ 两对平面，3D情况可类推：

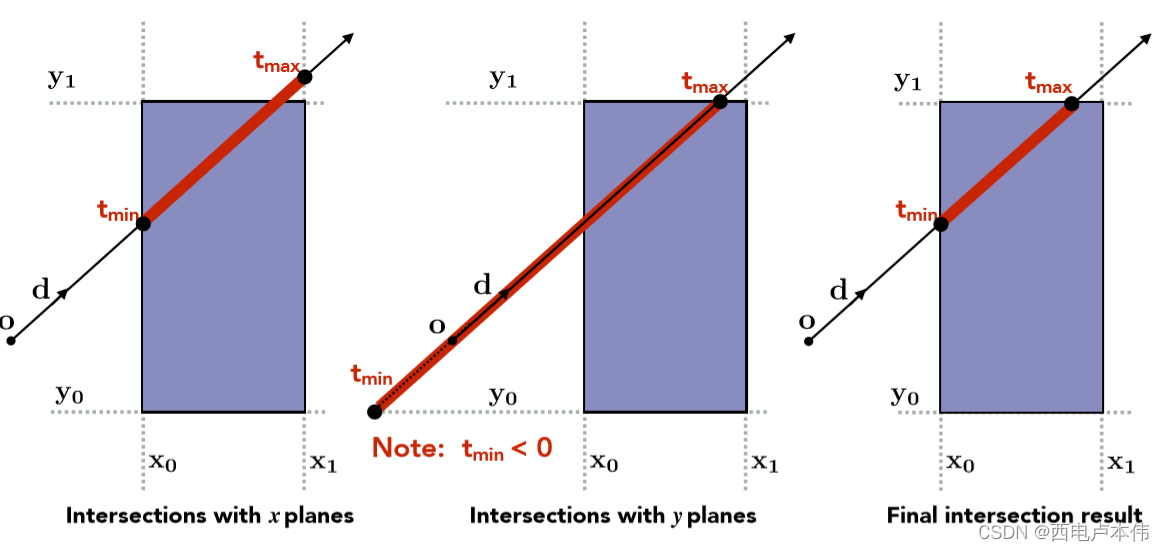
如上图最左边所示，求出光线与 $x$ 平面的交点，将先进入的交点（偏小的那个）记为 $t_{min}$， 后出去的交点（偏大的那个）记为 $t_{max}$，紧接着如中间图所示计算出光线与y平面的两个交点同样记为另外一组 $t_{min}$ 和 $t_{max}$，当然计算的过程中要注意如果任意的 $t<0$，那么这代表的是光线反向传播与对应平面的交点。

我们得到了光线与一对 $x$ 平面的交点，与一对 $y$ 平面的交点，究竟哪些点才是真正与盒子的交点呢？要明白：

1. 只有当光线进入了所有的平面才算是真正进入了盒子中
2. 只要当光线离开了任意平面就算是真正离开了盒子

所以对每对平面的 $t_{min}$ 和 $t_{max}$ 做如下运算：
$$t_{enter}=max[t_{min}]t_{exit}=min[t_{max}]$$其中 $t_{enter}=max[t_{min}]$ 和 $t_{exit}=min[t_{max}]$ 分别对应了上述两点条件，而对应所举的2D例子，最终求出了两个真正的与包围盒的交点如最右边图所示。图形上可以理解为两者交集。

光线一定会与包围盒有交点吗？显然不是，那么什么条件下才会有交点呢？

当 $t_{enter}<t_{exit}$ 的时候，光线所在直线一定在盒子中待过一段时间，也必然存在交点。但光线并不是直线，而是射线，除了保证了光线所在的直线在盒子里待过一段时间，还要考虑实际物理意义，具体如下：

当 $t_{exit}<0$ 时，可以想象光的起始点是在物体之前，所以才需要反向延伸，这种情况下是不可能有交点的。而 $t_{exit}>=0，t_{enter}<0$ 时，对应光的起始位置原本就在包围盒内，所以一定与之相交。综上，光线与包围盒有交点的充分必要条件为：
$$t_{enter}<t_{exit}{t}_{exit}>=0$$包围盒也是曲面（特殊的曲面，与 $xyz$ 轴垂直），自然可以用显示曲面的方法计算交点，直接套用得到：

均匀网格（Uniform Grids）

现在已经可以通过事先对每个物体求一个包围盒，在与三角形面求交之前先对包围盒求交，达到不错加速效果。但是考虑这样两个极端情况：

1. 整个场景只有一个极其复杂的单一人物模型，那么只对这一个物体做包围盒的话，相当于对效率没有任何提升
2. 整个场景充斥着大量的细小模型，如草，花之类的，每个模型可能只有很少的面，如果此时对每个物体求包围盒，得到的包围盒数量会相当之多，对于光线追踪效率来说效率提升有限

基于以上两点考虑，AABB并不应只局限于以物体模型为单位，可以更加精细的考虑到以面为单位。另外对于场景的许许多多包围盒来说应该要有一种数据结构将其统领起来。因此如何更好的划分场景形成不同的AABB，使得划分之后的AABB能够更好的加速光线追踪，这就是接下来要考虑的问题关键！

最简单的划分方法，均匀网格。

第一步对所要考虑的场景找一个包围盒，第二步均匀划分这个大包围盒成网格，第三步在每个重叠小包围盒上存储物体模型信息，最后根据光线的方向与判断出所有相交的方格（这一步可以利用bresenham算法，移步至直线光栅化了解），倘若方格中存储有物体，再进一步与方格中的物体模型或是面求交。

以上就是均匀网格划分的全部过程了，简单来说就是将空间划分为多个均匀的小的AABB，再根据光线方向找出相交grid（这一步并不需要判断所有方格，可以用brenham类似的方法来做），再判断grid中是否存储了模型信息，若有则进一步求交。（这种划分方法假设了找出相交方格要比直接判断与物体求交相对容易，因此划分方格数的多少也是性能的关键：方格太少，没有加速效果；方格太多，判断与方格的求交可能会拖累效率）

因此这种方法最适合的场景就是空间中均匀布满了三角形面，如下图这种场景：

如果说场景较为空旷，物体较小且分离得比较开，那么均匀分割的效果就会很差了，因为会有很多无效的方格与光线的求交过程。

KD-Tree空间划分（Spatial Partitions）

一些常用的空间划分方法：

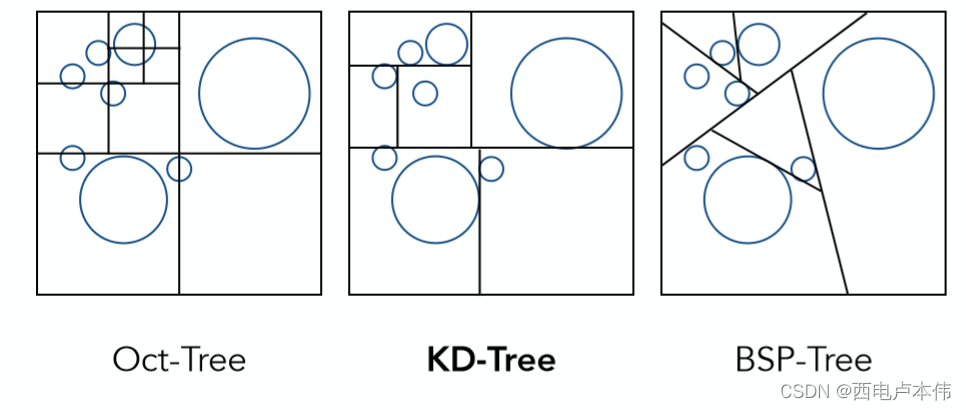
第一种Oct-Tree，也就是八叉树，每次将空间分为8个相等的部分，再递归的对子空间进行划分。因为图中是2维例子，所以只划分了4部分。当划分的子空间足够小或是空间中三角形面的数量很少的时候会停止划分。这种方法的显著缺点是，随着维度的上升划分的空间数量会呈指数级增长。

第二种KD-Tree，其每次将空间划分为两部分，且划分依次沿着 $x-axis，y-axis，z-axis$ （保持最规整的空间区域），如图中所示，第一次横着将2维空间分为上下，第二次再竖着将上下两个子空间分别划分为左右部分，依次递归划分，终止条件与八叉树类似。

第三种BSP-Tree，其与KD-Tree类似，唯一不同的是划分不再沿着固定一轴，可以任意方向划分，缺点自然是划分的空间没有规则性，求交困难。

为什么这种分法叫树？看下面的KD-Tree就可以知道答案。

第一步将空间分为两部分，第二步对左右两个子空间换个方向再分为两部分（这里只画出了有半部分）

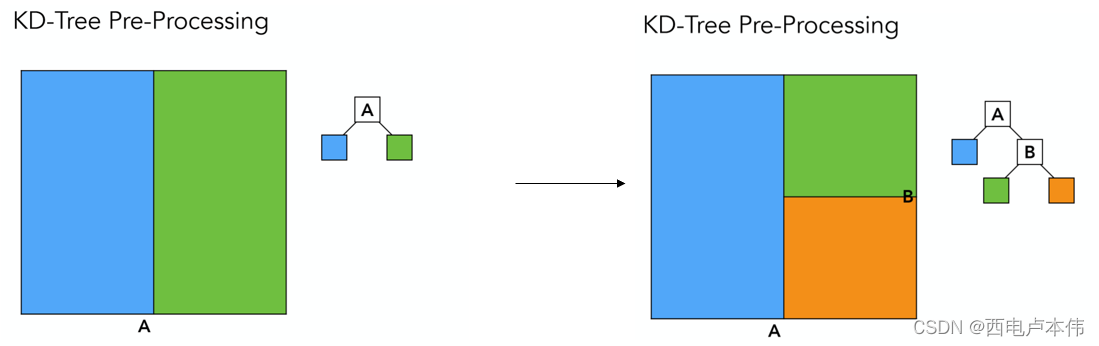
如此递归的划分下去，且在划分过程当中遵循这样几点：

1. 依次沿着 $x-axis,y-axis,z-axis$ 划分，使得空间被划分的更加平衡
2. 划分的位置由空间中三角面的分布决定，具体细节不展开
3. 叶子节点存储对应空间的所有物体或三角面信息，中间节点仅存储指针指向两个子空间
4. 当划分空间太小或是子空间内只有少量三角形则停止划分

当KD-Tree建立完成之后，如何进行光线与物体求交判断呢？过程如下：

第一步判断光线是否与最外层的包围盒相交，如果相交进一步判断是否与对应的两个子空间相交（因图中做了简化，最大包围盒的左半边并没继续进行划分，实际上应该要划分的，所以左半部分对应的1号空间是叶子节点），如果光线与之相交，进一步判断与存储与叶子节点的物体信息求交。左半边判断完之后，接着判断右半部分，同样如果对于有半部分存在相交情况，则对于右半部分的所有子空间，递归的执行这个步骤即可。

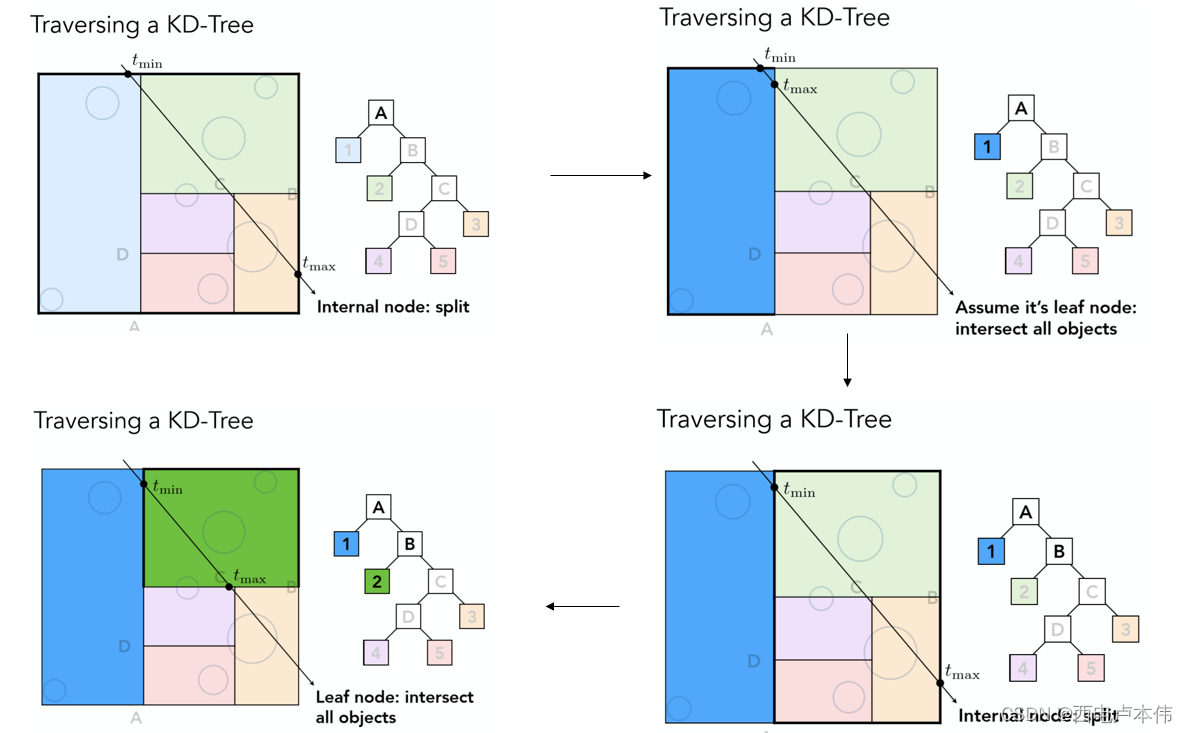
优点：

利用KD-Tree的结构来构建AABB的好处是倘若光线与哪一部分空间不相交，那么则可以省略该部分空间所有子空间的判断过程，在原始纯粹的AABB之上更进一步提升了加速效率。

缺点：

缺点是判断包围盒与三角面的是否相交较难，因此划分的过程不是那么想象的简单，其次同一个三角面可能被不同的包围盒同时占有，这两个不同包围盒内的叶节点会同时存储这一个三角形面。

KD-Tree划分方法技术在业界之中逐渐不再被使用，但依然有很多借鉴参考价值。

Bounding Volume Hierarchy（Object Partitions）

BVH与前几种方法最显著的区别就是，不再以空间作为划分依据，而是从对象的角度考虑，即三角形面，过程如下：

第一步同样找出场景的整体包围盒作为根节点，第二步找到合适的划分点，将最大包围盒内的三角形面分为两部分，再分别重新就算新的包围盒，此时包围盒会重叠，但一个三角形面只会被存储在唯一的包围盒内，而这也就解决了KD-Tree的缺点！

接下来与KD-Tree的建立类似，递归的对所有子空间重复该步骤

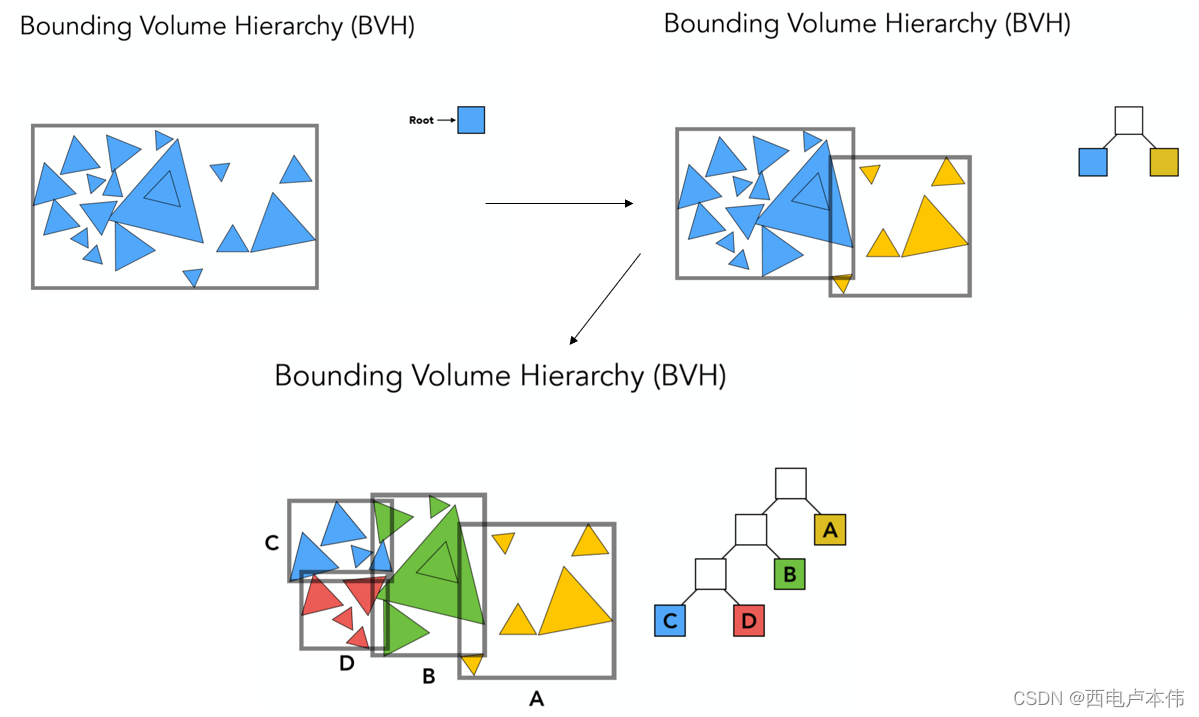
最终可以建立出如上图的所示的树形结构，同样为了画图方便，只进行了左半部分的划分，右半部分其实同理。

细节：

1. 每次划分一般选择最长的那一轴划分，假设是x轴，那么划分点选择所有三角面的重心坐标在x坐标上的中位数进行划分，如此便能保证划分的三角形左右两边三角形数量尽可能差不多，当然也就使得树形结构建立的更加平衡，深度更小，平均搜索次数更少，提高了效率，学过数据结构的应该都知道。
2. 与KD-Tree一样，中间节点不存储物体三角面信息，只在叶节点中存储，终止条件可设定为当前包围盒内三角形数量足够少。

最后给出这样一个BVH加速结构遍历节点的伪代码参考：

Intersect(Ray ray, BVH node){
	if (ray misses node.bbox) return;              //光线与包围盒不相交
	if (node is a leaf node )                      //光线与包围盒相交且交点位于叶子节点
		test intersection with a1l objs;           //光线与叶子节点中存储的物体信息进行求交
		return closest intersection;
    
	hit1 = Intersect(ray, node.child1);            //递归计算左孩子
	hit2 = Intersect(ray, node.child2);            //递归计算右孩子
	return the closer of hit1, hit2;               //返回值为最近的交点
}

至此，基本的基于Whitted-Style光线追踪的知识到此为止，以下部分为进阶部分。

辐射度量学（Radiometry）

为什么突然扯这个？

在Blinn-Phong模型中，我们时如何定义光线的，好像根本就没有定义。就算最基本的光的强度我们都是简单的用 $I$ 来表示。这肯定是不对。其次，上述的Whited-Style光线追踪模型，它真的是一个正确的模型吗？显然不是，原因如下：

1. whited-style光线追踪只考虑了光滑面的镜面反射与折射，并没有对漫反射的光线进行追踪，而是直接返回当前着色点颜色
2. 在计算光源直接照射的贡献时，使用了Blinn-Phong模型，而Blinn-Phong模型本身就是一个不准确的经验模型，使用的这种模型的whited-style光线追踪自身自然也是不正确的

为此，更好的渲染模型路径追踪出现了，而在这之前，我们必须掌握一些辐射度量学的知识，它是对光照的一套测量系统和单位，能够准确的描述光线的物理性质。

一些必要定义

辐射能量（Radiant Energy）和辐射通量/功率（Radiant Flux/Power）

首先看一看Radiant energy的定义：

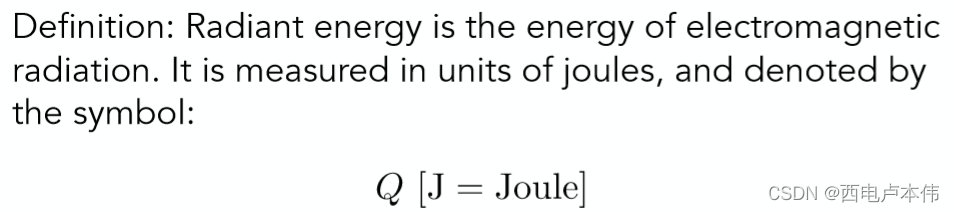
所谓辐射能量其实非常直观，就是辐射出来的电磁能量，单位为焦耳。可以用物理当中的做功的大小来进行类比。

接下来是Radiant flux(power)：

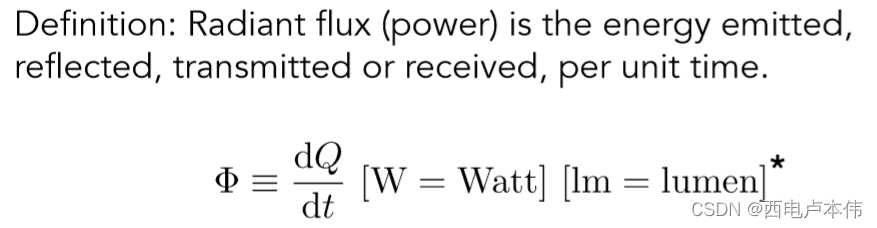
所谓辐射通量或者说辐射功率，其实就是在辐射能量的基础之上除以时间，也就是单位时间的能量。同样也可以用物理当中的功率来进行类比。

辐射强度（Radiant Intensity）

Radiant itensity是指从一个光源出发某一方向上的亮度。看它的数学定义：

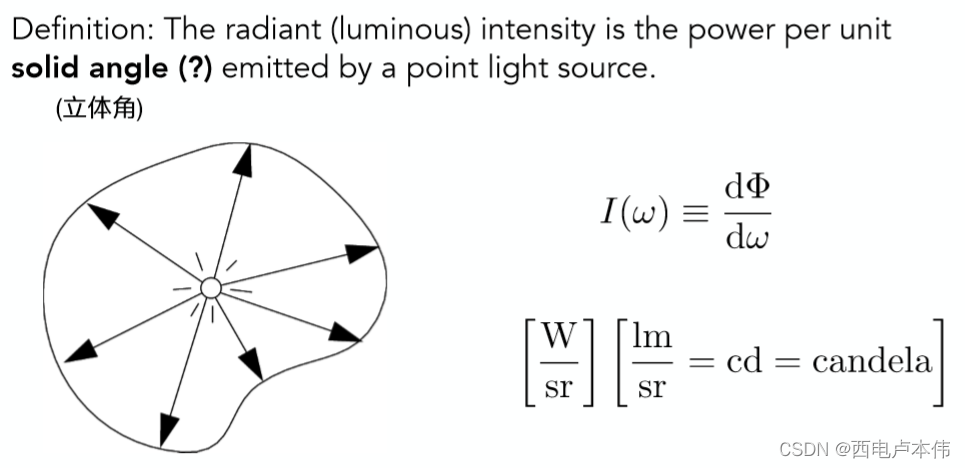
概括来说就是从光源发出的每单位立体角上的功率。立体角（solid angle）又是什么？

solid angle其实就是对应二维空间中圆的弧度在三维空间中球上的拓展。首先看在二维计算弧度公式如下：

即 $\theta =\frac{l}{r}$ (中学知识)，那么对应在三维上的球的弧度(立体角)，只需进行一个简单的扩展如下：
即立体角度所对应球上的投影面积比上半径的平方，整个球的立体角为 $4\pi$（整个球的面积是 $4{\pi }^2{r}^2$，再除以 $r^2$）。

那么对于Radiant intensity的定义当中，微分立体角 $d\omega$ 计算如下：

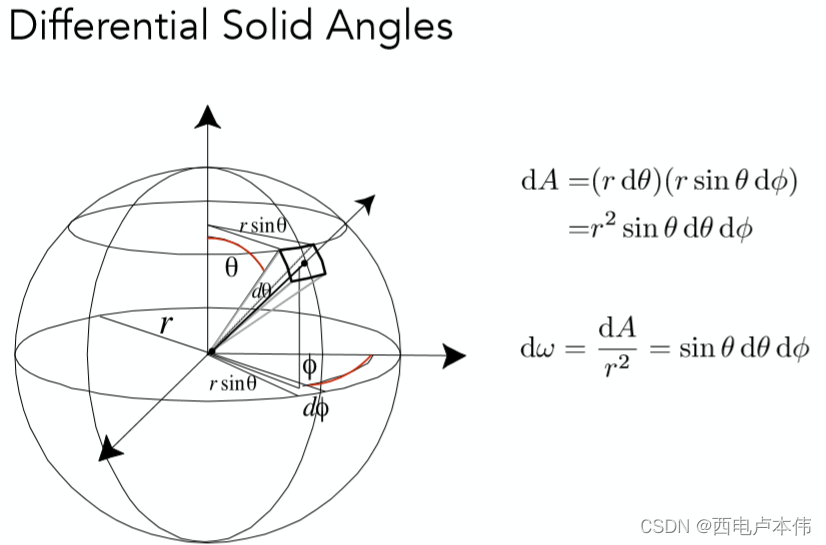
这图就跟那高数书上二重积分一样一样的。首先确定空间中一个方向（通过 $\theta ,\varphi$），在这两个角度上分别增加一个微分值，则可以计算出如图中所示的对应到球上的投影面积。其中 $rd\theta$ 就是微分面积元的高，$rsin\theta d\varphi$是微分面积元的宽，二者相乘，自然就是面积了，再根据立体角的定义除以 $r^2$ 即可得到微分立体角了。

上述确定空间中一个方向（通过 $\theta ,\varphi$），这个方向就是为 $\omega$，然后才在此基础之上分别对 $\theta ,\varphi$ 增加 $d\theta ,d\varphi$ 经计算得到最终的 $d\omega$ ，因此Radiant intensity的物理含义此时就很清楚了，为光源向某一方向所发射出的单位立体角的功率，简而言之就是光源在某个方向上的亮度。（一定要弄清，不然极有可能和下面两个概念弄混）

最后举一个对各向同性点光源计算Radiant intensity的例子：

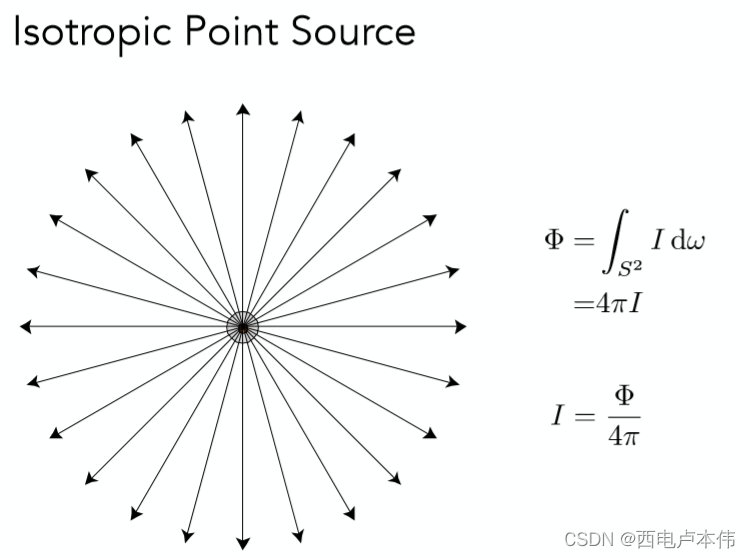
因为各项同性点光源所有方向上的亮度都与方向无关，因此立体角可以直接积分出来为 $4\pi$，最终计算得 $I=\frac{\Phi }{4\pi }$。

irradiance

没有合适的中文翻译，直接用英文了。来看irradiance的数学定义：

由图可见，irradiance是指每单位照射面积所接收到的power。回想Blinn-Phong模型漫反射那个部分，我们考虑光线强度与什么有关呢？是入射光线与着色点的夹角以及光线自身的强度。在入射光线与着色点的夹角这块，着重强调了我们需要乘上一个 $cos\theta$。此外，光线自身的强度越远会越加衰减：

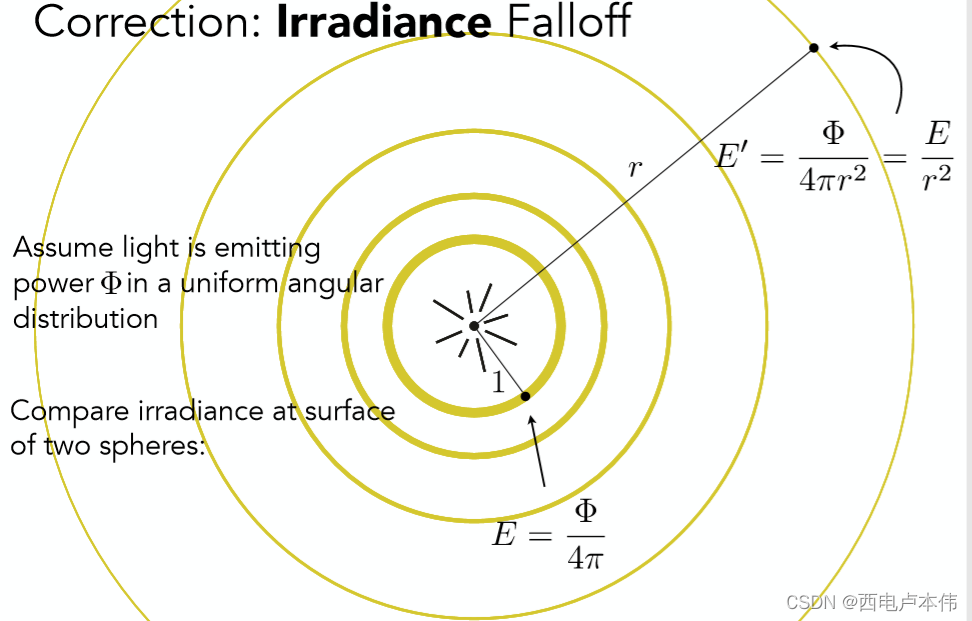
该现象完全可以用irradiance解释，因为光的功率始终一致，离点光源所照射到的圆球面积也就越大，因此根据irradiance的式子，分母的面积值也就越大，irradiance也就越小。

radiance

最后来看radiance的定义：

radiance就是指每单位立体角，每单位垂直面积的功率，直观来看的话，很像是Intensity和irradiance的结合。它同时指定了光的方向与照射到的表面所接受到的亮度。

但这里有一个细微的区别，在irradiance中定义的每单位照射面积，而在radiance当中，为了更好的使其成为描述一条光线传播中的亮度，且在传播过程当中大小不随方向改变，所以在定义中关于接收面积的部分是每单位垂直面积，而这一点的不同也正解释了图中式子分母上的 $cos\theta$ ，具体可以观察如下图：

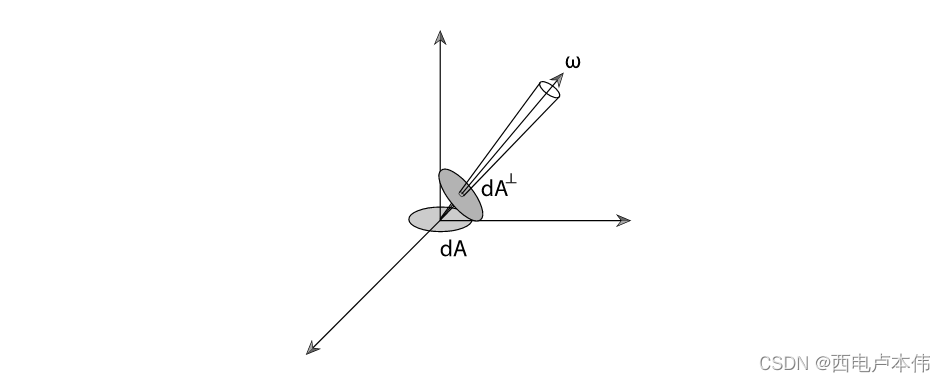
即图中的 $dA$ 是irradiance中定义所对应的，而 $d{A}^{\perp }$才是radiance中所定义的面积。二者之间的关系为$d{A}^{\perp }=dAcos\theta$。

在理解了radiance和irradiance的定义之后，再讨论讨论它们之间的关系，通过二者的定义式子，不难得出如下结果：
$$L(p,\omega )=\frac{dE(p)}{d\omega cos\theta }$$进一步推导得到：

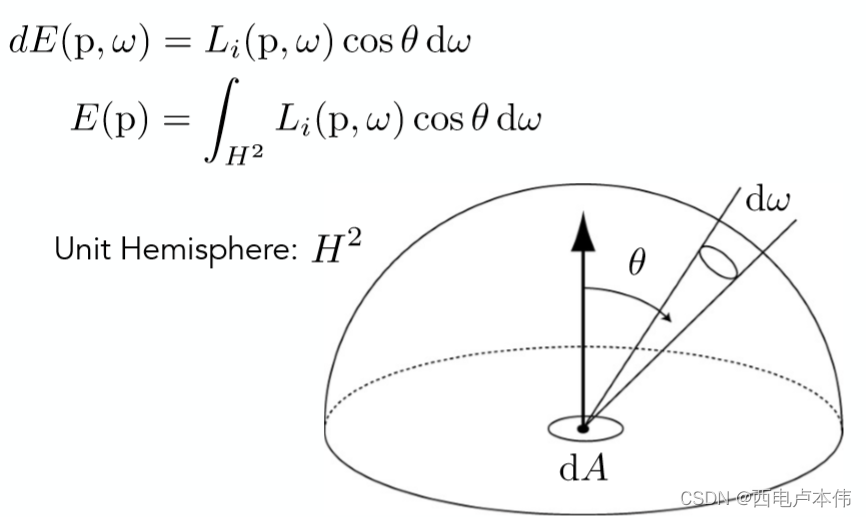
观察一下积分后的式子，$E(p)$ 就是点 $p$ 的irradiance，其物理含义是上文所提到过的点 $p$ 上每单位照射面积的功率，而 $L_i(p,\omega )$ 是radiance，指入射光每立体角，每垂直面积的功率，因此积分式子右边的 $cos\theta$ 解释了垂直面积，而对 $d\omega$ 积分，则是相当于对所有不同角度的入射光线做一个求和。那么该积分式子的物理含义便是，一个点（微分面积元）所接收到的亮度（irradiance），由所有不同方向的入射光线亮度（radiance）共同贡献得到。

双向反射分布函数（BRDF）

通过上述所有辐射度量学各种概念的定义之后，我们可以从这样一个角度理解光线的反射，如下图所示：

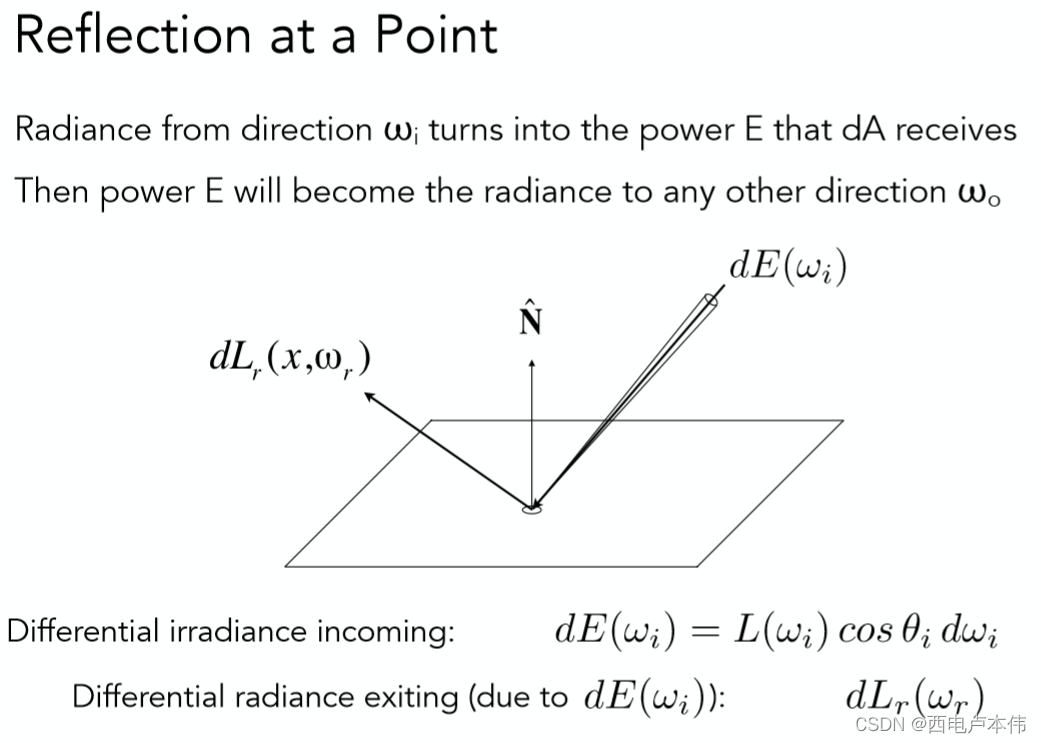
一个点（微分面积元）在接受到一定方向上的亮度（$dE({\omega }_i)$）之后，再向不同方向把能量辐射出去（$d{L}_r({\omega }_r)$）

直观的理解，不同物体表面材质自然会把一定方向上的入射亮度 $dE({\omega }_i)$ 反射到不同的方向的光线上 $d{L}_r({\omega }_r)$。用上述概念解释，就是着色点所收到的irradiance经过反射产生radiance到其他方向。如理想光滑表面会把入射光线完全反射到镜面反射方向，其它方向则完全没有；如理想粗糙表面会把入射光线均匀的反射到所有方向。因此所谓BRDF就是描述这样一个从不同方向入射之后，反射光线分布情况的函数，定义如下：

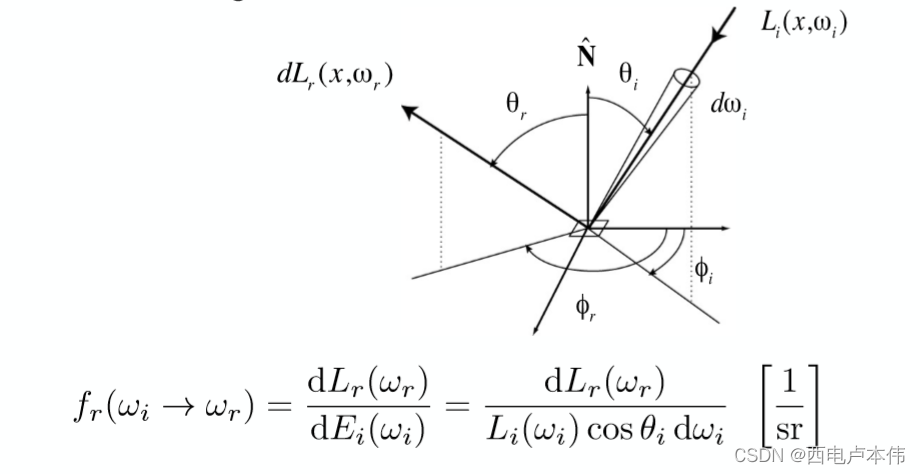
上图中下方的式子即为BRDF，它就收两个参数入射光方向 ${\omega }_i$，反射光方向 ${\omega }_r$，函数值为反射光的radiance与入射光的irradiance的比值。

借助BRDF，可以定义出反射方程如下：

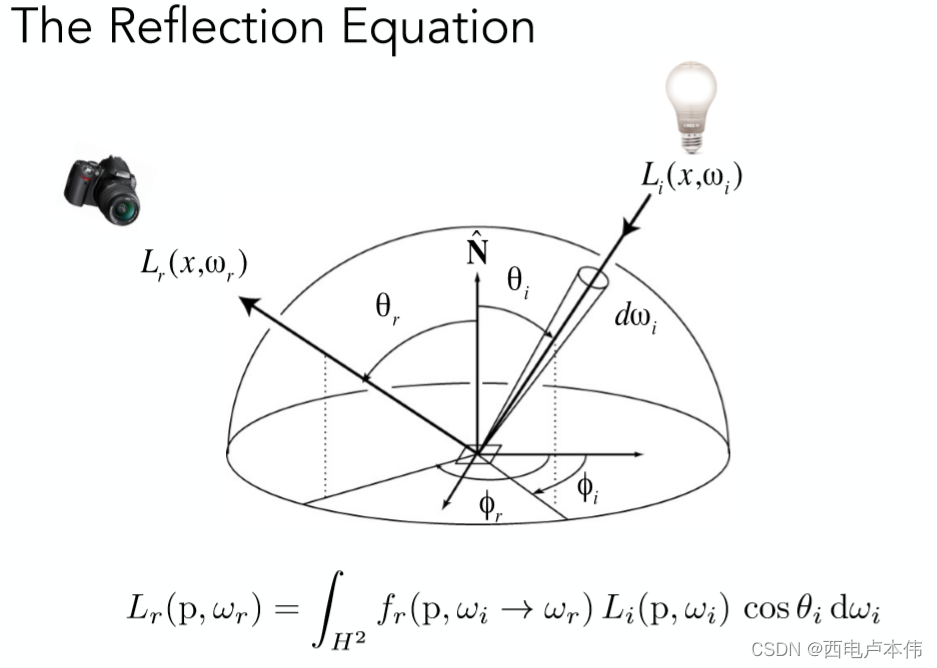
即摄像机所接受到的 ${\omega }_r$ 方向上的反射光，是由所有不同方向上入射光线的irradiance经过反射贡献得到的（图中式子的$L_i\left(\mathrm{p},{\omega }_i\right)\cos {\theta }_i\mathrm{d}{\omega }_i$），而不同方向入射光线的irradiance对反射方向 ${\omega }_r$ 的贡献程度则由物体表面材质决定，所以乘上了一个BRDF函数。如果对上述几个物理量的定义明确的话，这个式子并不难看懂。

至此通过辐射度量学，以及BRDF最终得到的反射方程正是一个几乎完全正确的光照模型了。再仔细观察一下反射方程：

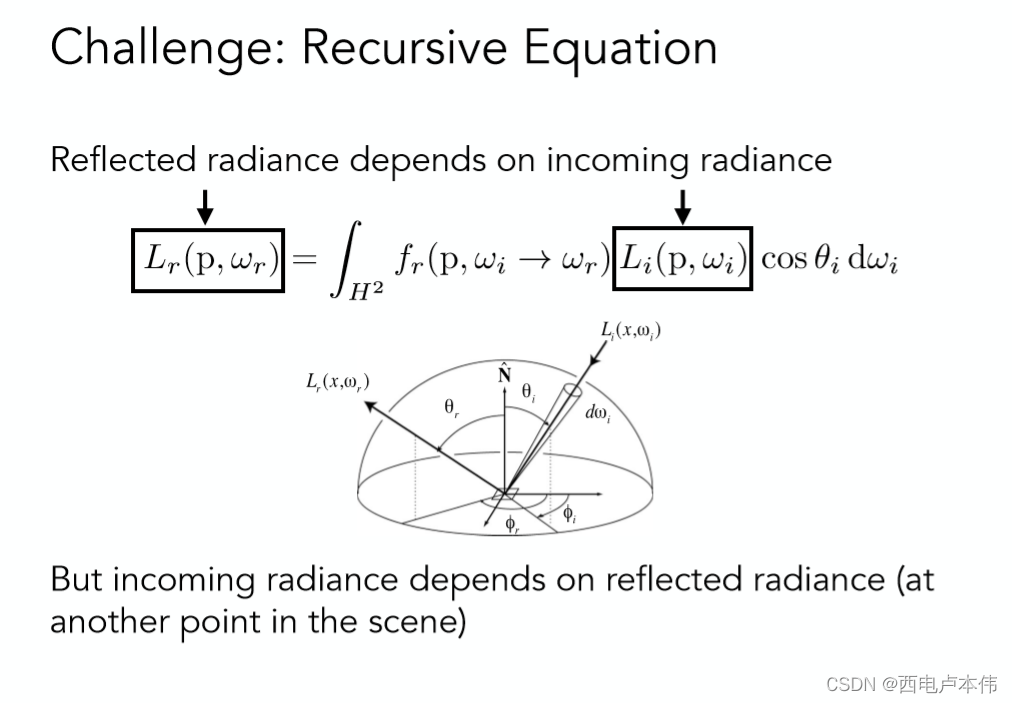
不难发现，入射光线的radiance不仅仅是光源所造成，还有可能是其他物体上着色点的反射光线的radiance，恰好反射到当前的着色点，而其他物体上的反射光线的radiance依然也是这么个情况。这与whitted-style当中的光线追踪过程十分类似，也是一个递归的过程，所以说想要解这样一个方程还是比较难的。

渲染方程（The Rendering Equation）

反射方程明白了，渲染方程也就水到渠成。上述我们并没有讨论物体自身的发光情况，渲染方程就是在反射方程的基础之上添加了一个自发光项（Emission term）：
$$L_o(p,{\omega }_o)=L_e(p,{\omega }_o)+{\int }_{{\Omega }^{+}}{L}_i(p,{\omega }_i)f_r(p,{\omega }_i,{\omega }_o)(n\cdot {\omega }_i)d{\omega }_i$$其中 $L_e(p,{\omega }_o)$ 为自发光项，反射方程中的 $cos\theta$ 用 $n\cdot {\omega }_i$代替。

接下来从一个点光源和单个物体的场景开始理解渲染方程：

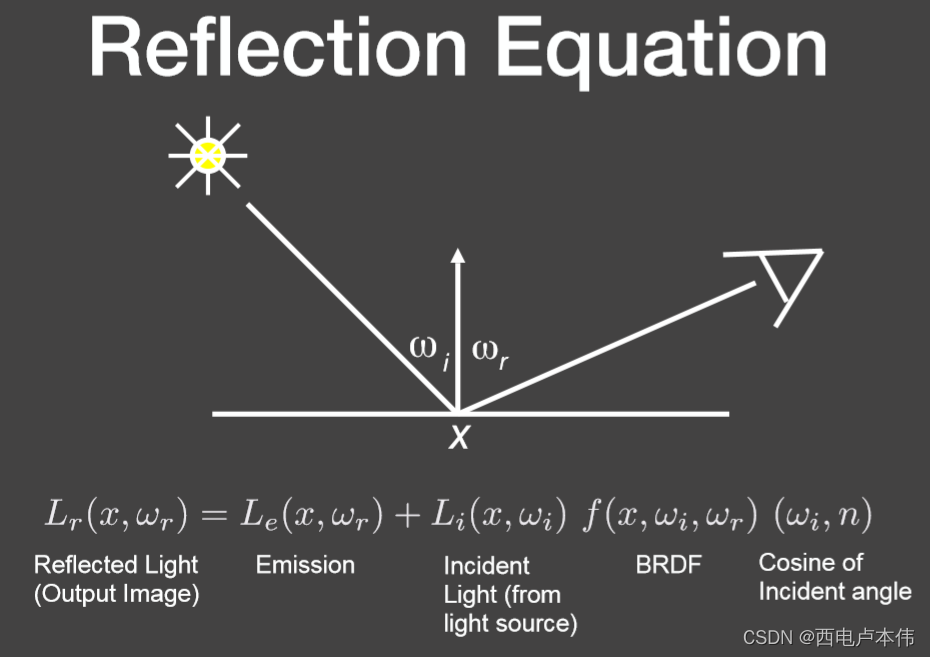
点光源对一个点来说自然只有一个方向有入射光，所以这里没有了积分。多个点光源照射一个物体的情况：

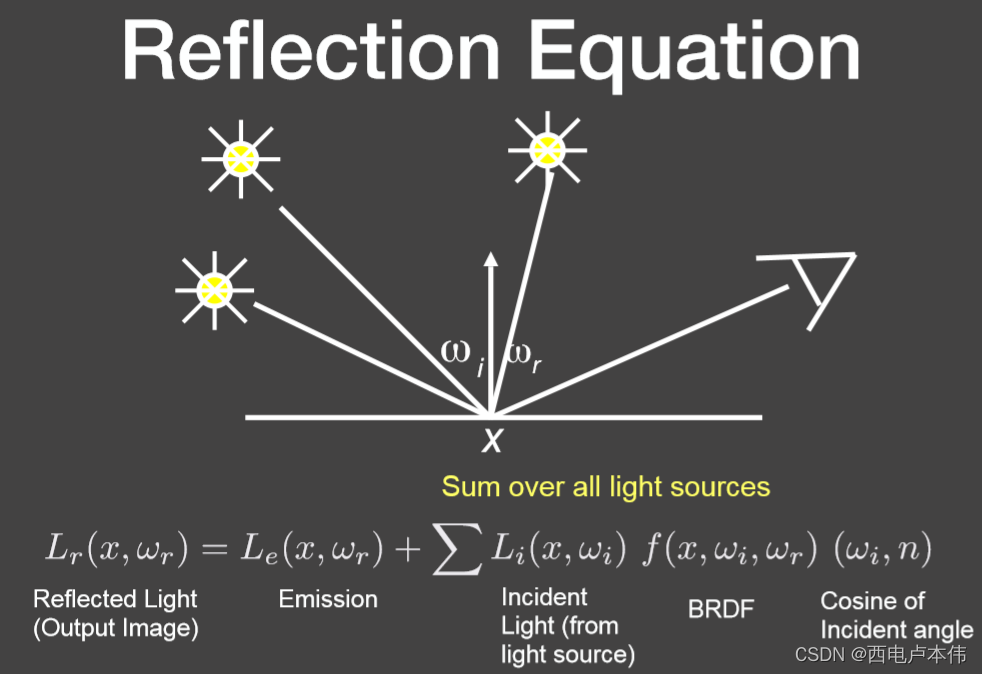
将这些所有的点光源的贡献全部求和即可，那么如果点光源变成了面光源呢？如下图所示：

其实面光源就相当于无穷多个点光源的集合，只需要对面光源所在的立体角范围进行积分，并且能够确定不同立体角方向的面光源的入射光radiance即可。那么更进一步再在场景当中加入其它物体，使得物体之间发生光线交互之后是什么情况呢：

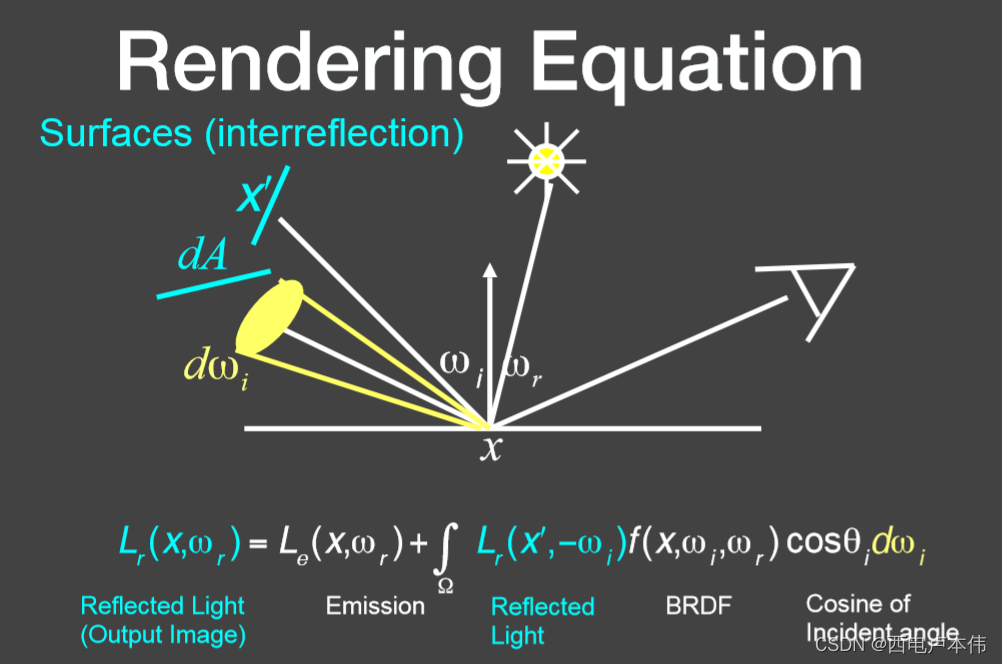
如上图所示，可以把其它物体同样考虑成面光源，对其所占立体角进行积分即可，只不过对其它物体的立体角积分不像是面光源所有入射方向都有radiance，物体的立体角可能只有个别几个方向有入射的radiance（即多次物体间光线反射之后才恰好照射到着色点），其它方向没有，但本质上都可以视作是面光源。

观察一下图中的渲染方程可以发现除了两个入射和反射的radiance，其它所有项都是知道的，可以将上式进一步写成如下图下方所示的式子：

其中各项与原渲染方程中一一对应（这种简写在数学中很常见），再接着进一步化简，把该式子离散化写为线性的形式：

经过两步不是很清楚但其实是正确的数学推导之后（狗头），得到了这样一个式子：
$$L=E+KL$$其中 $L$ 其实就是想要求得的反射光，$E$ 是自发光其实就是光源的发光项，$K$可以理解为对光线进行反射的一种算子操作。那么利用线性代数的知识很容易就可以推导出 $L$ 的结果如下：

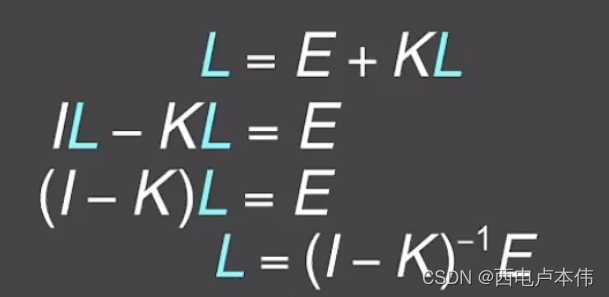
其中 $I$ 为单位矩阵，再接着对 $(I-K{)}^{-1}$ 使用广义二项式定理得到：

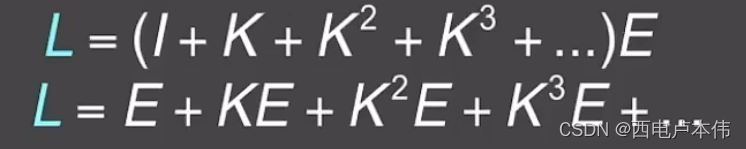
仔细观察这个式子，注意 $E$ 是光源所发出的光，$K$ 为反射算子，这样一个式子的物理含义如下图所示：

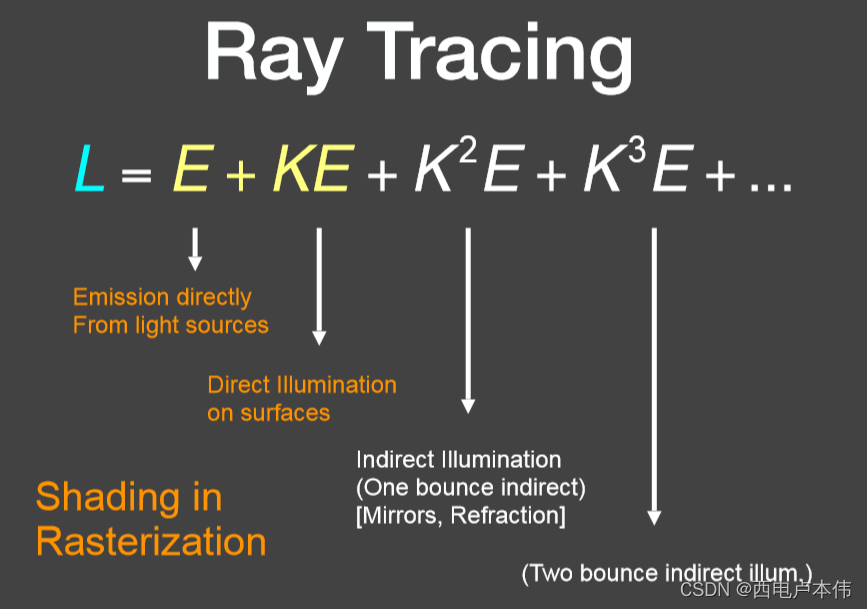
$E$ 为自身发出的光，$KE$ 则代表对光源反射一次的结果，即直接光照，那么前两项之和就是光栅化当中Blinn-phong模型着色所考虑的结果。而对于全局光照来说，可不能就考虑这么几项，光在空间中是经过无数次的反射折射的，故方程正确地考虑了 $K^{2}E$ ，即一次弹射的间接照明，$K^{3}E$ 就是两次弹射的间接照明，依次类推。

一次反射直接光照，没有被光照直接照射的地方全部都是黑色的：

两次反射，考虑到一次弹射的间接光照，没有被光源直接照射的地方由于收到了其他物体反射过来的光，不再是黑色：

三次反射，考虑到两次弹射的间接光照，相较于两次又有新的反射折射，亮度继续增加：

但光线能量传播终究是有损失的，越来越多的反射折射会使得增加的亮度越来越少，最终收敛于一个峰值。

路径追踪（Path Tracing）

可以看看英伟达的官博 What Is Path Tracing?

其中给了这么一幅图：

可以看到效果还是挺明显的，path tracing更加炫酷（但我为啥觉得ray tracing更真实呢哈哈）。总之来说，path tracing相较于ray tracing有更好的渲染效果（上面介绍辐射度量学就说了）。

要想实现路径追踪，就要用到上述的渲染方程，具体定义及数学公式是给出来了，但是如何解是一个问题。为此，引入蒙特卡洛积分。

蒙特卡洛积分（Monte Carlo Integration）

蒙特卡洛积分的目的： 当一个积分很难通过解析的方式得到答案的时候可以通过蒙特卡洛的方式近似得到积分结果，如下图所示：

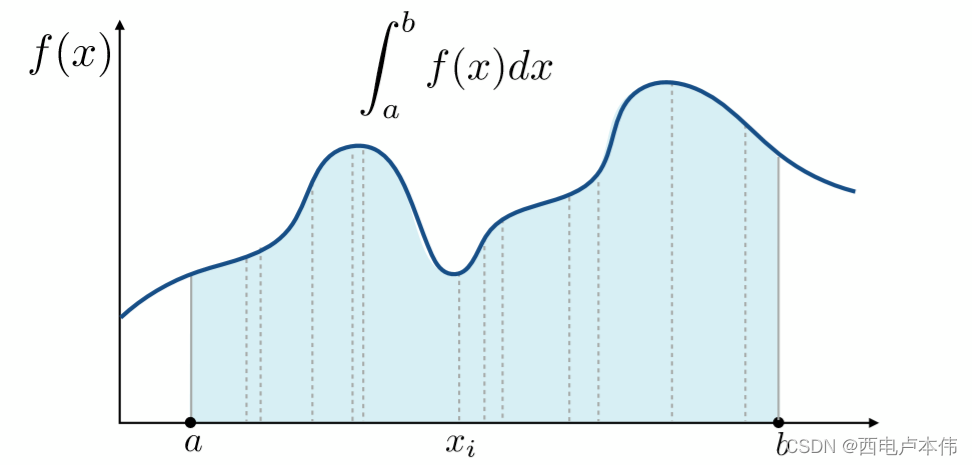
显然对于这样一个函数，很难去用一个数学式子去表示，因此无法用一般解析的方法直接求得积分值，而这时候就可以采用蒙特卡洛的思想了。

蒙特卡洛积分的原理及做法： 对函数值进行多次采样求均值作为积分值的近似。

该做法十分容易理解，想象一下如果对上图这个函数值进行均匀采样的话，其实就相当于将整个积分面积切成了许许多多个长方形，然后将这些小长方形的面积全部加起来。它可以指定一个分布来对被积分的值进行采样，定义如下：

如图所示，我们希望求出一个函数 $f(x)$ 在积分域 $[a,b]$上的积分值，选定一个采样的分布 $p(x)$，概率论中称之为概率密度函数。

在数学中，连续型随机变量的概率密度函数（probability density function，pdf），在不至于混淆时可以简称为密度函数，是一个描述这个随机变量的输出值，在某个确定的取值点附近的可能性的函数。而随机变量的取值落在某个区域之内的概率则为概率密度函数在这个区域上的积分。当概率密度函数存在的时候，累积分布函数是概率密度函数的积分。概率密度函数一般以小写标记。

满足的性质：${\int }_{-\infty }^{+\infty }f(x)dx=1$

为了方便，所有的采样都使用均匀采样，因此很容易推出：

我们只需要知道，蒙特卡洛在此来说就是一个帮助求得困难积分值的方法，具体方法是用采样点的函数值除以该点的概率密度，将所有点所得的值相加最后取平均数即得所求函数得定积分值。

蒙特卡洛路径追踪（Monte Carlo Path Tracing）

有了这个基础，我们就可以解渲染方程了，先回顾一下：
$$L_o(p,{\omega }_o)=L_e(p,{\omega }_o)+{\int }_{{\Omega }^{+}}{L}_i(p,{\omega }_i)f_r(p,{\omega }_i,{\omega }_o)(n\cdot {\omega }_i)d{\omega }_i$$要想解出以上方程的解主要有两个难点：

1. 积分的计算
2. 递归形式

我们先对渲染方程做出一点小修改，先不考虑发光项 $L_e(p,{\omega }_o)$，以方便进行计算推导：
$$L_o(p,{\omega }_o)={\int }_{{\Omega }^{+}}{L}_i(p,{\omega }_i)f_r(p,{\omega }_i,{\omega }_o)(n\cdot {\omega }_i)d{\omega }_i$$观察该修改过之后的方程其实就只是一个单纯的积分计算了，其物理含义为着色点 $p$ 到摄像机或人眼的Radiance值。

从具体例子出发，首先仅仅考虑直接光照：

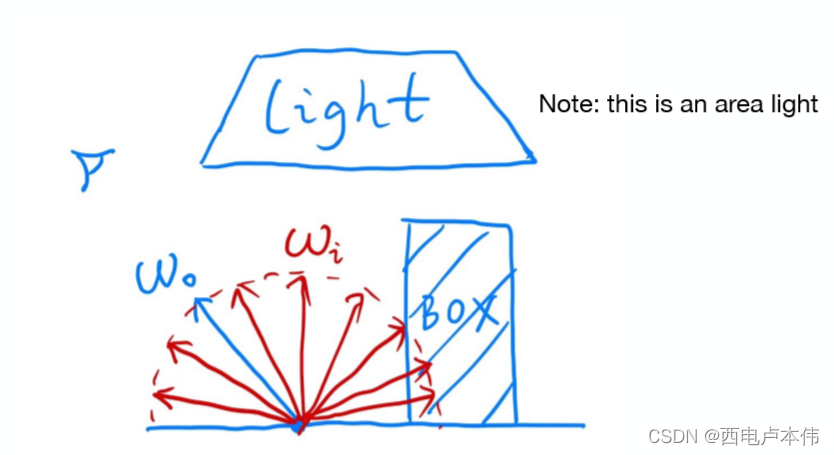
由蒙特卡洛积分我们知道，对于一个困难积分只要选定一个被积分变量的采样分布即可得到积分结果的近似值，而此时的被积分值为 ${\omega }_i$，选定 ${\omega }_i\sim p({\omega }_i)$ ，不难得出积分近似结果如下：
$$L_o(p,{\omega }_o)=\frac{1}{N}\sum _{i=1}^N\frac{L_i(p,{\omega }_i)f_r(p,{\omega }_i,{\omega }_o)(n\cdot {\omega }_i)}{p({\omega }_i)}$$单独考虑直接光照，因此只有当采样的方向 ${\omega }_i$ 击中光源的时候，光源才会对该着色点有贡献，计算伪代码如下：

显然单独仅仅考虑直接光照自然是不够的，还需要间接光照，即当采样的 ${\omega }_i$ 方向碰撞到了别的物体，如下图所示：

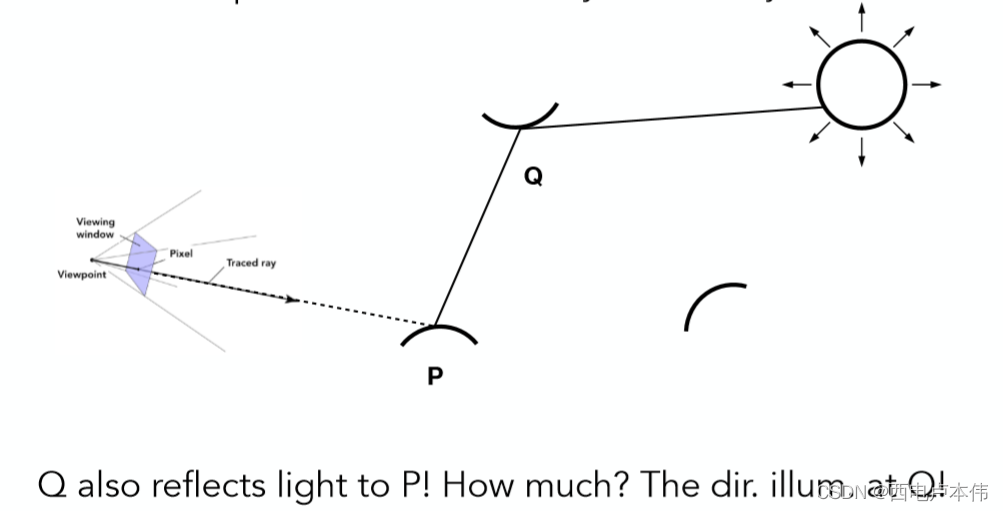
此时采样的光线碰撞到了另一个物体的 $Q$ 点，那么该条路径对着色点 $P$ 的贡献是多少呢？自然是在点 $Q$ 的直接光照再乘上反射到该方向上的百分比了。这是一个类似光线追踪的递归过程，不同在于该方法通过对光线方向的采样从而找出一条条可行的路径，这也正是为什么叫路径追踪的原因，伪代码如下：

至此，我们成功通过蒙特卡洛的方式解出了渲染方程的积分值，也通过考虑直接光照与间接光照解决了递归的问题。但该方法至此有一个非常致命的问题：

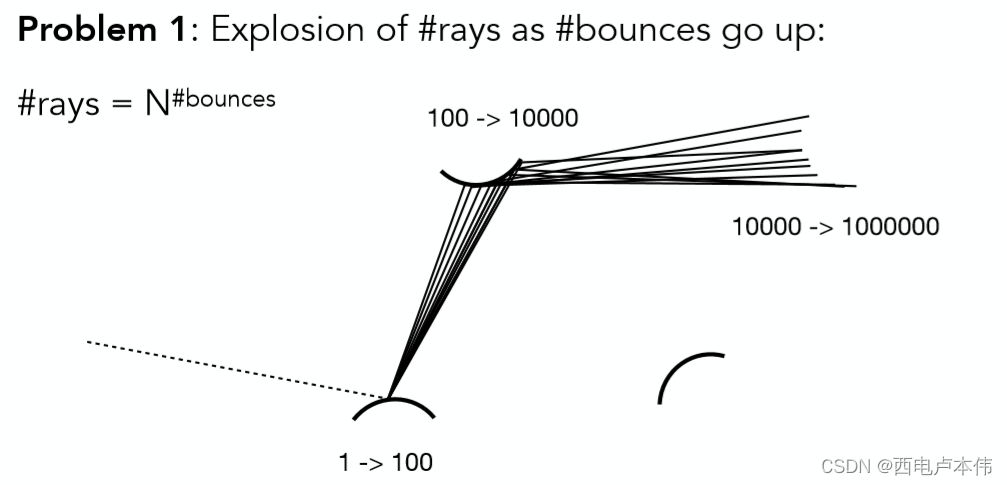
通过每次对光线方向的采样从而解出方程，假设每次采样100条，那么从人眼出发的第一次采样就是100条，在进行第二次反射之后再采样就是10000条，依次类推，反射越多次光线数量便会爆炸增长，计算量会无法负担，那么如何才能使得光线数量不爆炸增长呢？只有每次采样都只采用一个方向。

每次如果只采样一个方向那么所带来的问题也是显而易见的，积分计算的结果不准确，虽然蒙特卡洛积分是无偏估计，但样本越少显然偏差越大。但该问题很好解决，如果每次只去寻找一条路径结果不好，那么重复多次寻找到多条路径，将多条路径的结果求得平均即可。如下图所示：

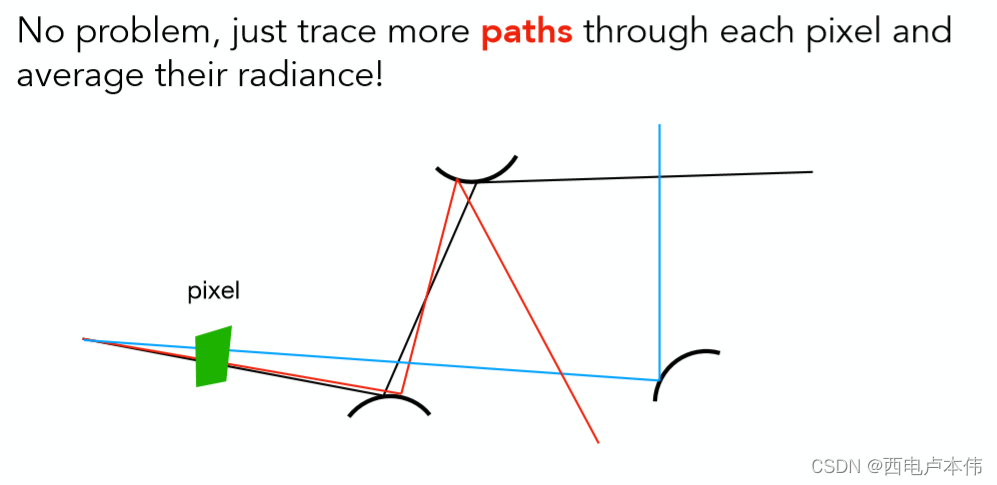
改良之后的Path Tracing伪代码如下：

通过对经过像素的光线重复采样，每次在反射的时候只按分布随机选取一个方向，解决了只对经过像素的光线采样一次，而对反射光线按分布采样多次所导致的光线爆炸问题。

那么现在所有的问题都解决了吗？还没有，之前一直强调的递归问题（上述中体现在shade函数里）没有解决。在现实世界中，光线确实无限折射反射的，但是在程序中我们要确保有穷性，但是人为给一个限定的反射限定次数又显得很怪（ray tracing中我们是这样做的），我们并不知道最好的反射次数是多少。这里十分精妙得采用了俄罗斯轮盘赌（Russian Roulette）。

给你一把左轮，两发子弹，你不知道哪一发会真正的射出子弹，因此拿这把左轮射自己，你有4/6的概率活下来，这就是俄罗斯轮盘赌的概念。将其应用在路径追踪当中，首先设定一个概率 $P$ , 有 $P$ 的概率光线会继续递归并设置返回值为 $L_o/P$ ，有 $1-P$ 的概率光线停止递归，并返回0。这样巧妙的设定之下光线一定会在某次反射之后停止递归，并且计算的结果依然是无偏的，因为Radiance的期望不变，证明如下：
$$E=P\ast \frac{L_o}{P}+(1-P)\ast 0=L_o$$shade函数的伪代码变更如下，使得可以停止递归了：

至此，路径追踪算法只剩最后一个小问题。就是效率非常的低下，如图所示：

在每次计算直接光照的时候，通过均匀采样任选一个方向，但只有较少得光线可以返回光源，尤其当光源较小的时候，这种现象越明显，大量采样的光线都被浪费了。

因此在计算直接光照的时候改进为直接对光源进行采样。这样所有采样的光线都一定会击中光源（如果中间没有别的物体），没有光线再会被浪费了。假设光源的面积为A，那么对光源进行采样的 $pdf=\frac{1}{A}$（因为 $\int \mathrm{pdf}dA=1$，概论密度函数性质），但原始的渲染方程：
$$L_o(p,{\omega }_o)={\int }_{{\Omega }^{+}}{L}_i(p,{\omega }_i)f_r(p,{\omega }_i,{\omega }_o)(n\cdot {\omega }_i)d{\omega }_i$$很明显是对光线方向 ${\omega }_i$ 进行积分的，如果想要对光源进行采样的并依然使用蒙题卡洛的方法，那么一定要将其修改为对光源面积 $dA$ 的积分，换言之就是需要找到 $dA$ 与 ${\omega }_i$ 的关系即可。如下图所示：

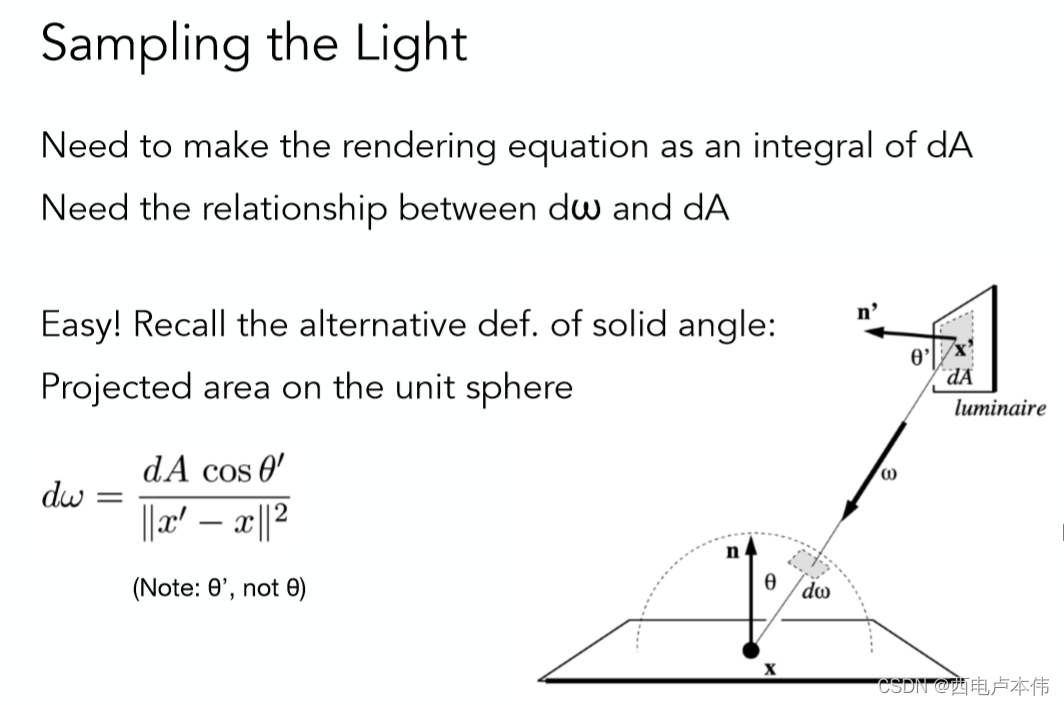
关系式中的 $cos{\theta }^{\prime }$ 是为了计算出光源上微分面积元正对半球的面积，之后再按照立体角的定义 $\mathrm{d}\omega =\frac{\mathrm{d}A}{r^2}$，除以着色点 $x$ 与光源采样点 $x’$ 距离的平方即可。于是根据图中二者的关系可将渲染方程改写如下：
$$L_o(p,{\omega }_o)={\int }_{{\Omega }^{+}}{L}_i(p,{\omega }_i)f_r(p,{\omega }_i,{\omega }_o)(n\cdot {\omega }_i)d{\omega }_i={\int }_A{L}_i(p,{\omega }_i)f_r(p,{\omega }_i,{\omega }_o)\frac{cos\theta cos{\theta }^{\prime }}{||x^{\prime }-x|{|}^2}dA$$这样便成功从 ${\omega }_i$ 积分转到了对光源面积 $A$ 的积分，就可以利用蒙特卡洛的方法对光源进行采样从而计算直接光照的积分值了，对于间接光照，依然采用先前的方法进行光线方向的均匀采样。最终伪代码如下，分直接光照和间接光照两部分计算：

计算直接光照的时候还需要判断光源与着色点之间是否有物体遮挡（上述我们假设了两者之间没有别的物体），该做法也很简单，只需从着色点 $x$ 向光源采样点 $x’$ 发出一条检测光线判断是否与光源之外的物体相交即可，如果有遮挡，直接光照这部分就没有了。如图所示：

至此，我们终于理顺了完整的路径追踪。整个过程还算是比较清晰的，发现问题解决问题，是学习任意一门学问都要经历的过程。