小批量梯度下降算法的Python实现

小批量梯度下降算法的核心思想仍然是基于梯度，通过对目标函数中的参数不断迭代更新，使得目标函数逐渐靠近最小值。它是批量梯度下降与随机梯度下降的折中，有着训练过程较快，同时又能保证得到较为精确的训练结果。在一些情况下，小批量梯度下降比批量梯度下降和随机梯度下降的速度都要快。

具体代码实现如下：

先导入要用到的各种包：

%matplotlib notebook
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

读入数据并查看数据的相关信息：

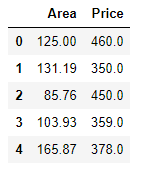
查看data中前五条数据：

data = pd.read_excel('gongyeyuan.xlsx','Sheet2')
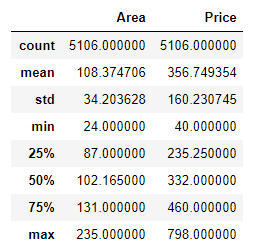
data.head()

查看data的各描述统计量信息：

data.describe()

绘制原始数据的散点图：

fig,axes = plt.subplots()
data.plot(kind='scatter',x='Area',y='Price',marker='o',color='k',ax=axes)
axes.set(xlabel='Area',ylabel='Price',title='Price vs. Area')
fig.savefig('p1.png')

向data中添加一列便于矩阵计算的辅助列：

data.insert(0,'Ones',1)
data.head()

小批量梯度下降的实现：

# 定义数据特征和标签的提取函数：
def get_fea_lab(train_data):
    
    cols = train_data.shape[1]
    X = train_data.iloc[:,0:cols-1]       # X取data中不包括索引列的前两列
    y = train_data.iloc[:,cols-1:cols]    # y取data中的最后一列
    
    X = np.matrix(X.values)
    y = np.matrix(y.values)
    
    return X,y


# 定义小批量样本的代价函数：
def computeCost(train_data,theta,k,mb_size):
    
    X,y = get_fea_lab(train_data)
    X = X[k:k+mb_size]
    y = y[k:k+mb_size]
    inner = np.power(((X*theta.T)-y),2)
    term = np.sum(inner)/(2*mb_size)
    
    return term


#定义小批量梯度下降函数：
def mb_gradient_descent(train_data,theta,alpha,mb_size):
    
    X,y = get_fea_lab(train_data)
    temp = np.matrix(np.zeros(theta.shape))      # temp用于存放theta参数的值
    parameters = int(theta.shape[1])             # parameter用于存放theta参数的个数
    m = len(X)                                   # m用于存放数据集中的样本个数
    cost = np.zeros(int(np.floor(m/mb_size)))    # cost用于存放代价函数
    st_posi = list(np.arange(0,m,mb_size))       # st_posi用于存放每次小批量迭代开始的位置
    new_st_posi = st_posi[:len(cost)]            # 去掉最后一次小批量迭代开始的位置
    k = 0
    
    for i in new_st_posi:
        
        cost[k] = computeCost(train_data,theta,i,mb_size)
        k = k + 1
        error = (X*theta.T) - y
        
        for j in range(parameters):
            
            t = np.multiply(error,X[:,j])
            term = t[i:i + mb_size]
            temp[0,j] = theta[0,j] - (alpha/mb_size)*(np.sum(term))
                            
        theta = temp
                            
    return theta, cost


# 初始化相关参数：
theta = np.matrix(np.array([0,0]))
alpha = 0.00001
mb_size = 50


# 调用随机梯度下降函数来计算线性回归中的theat参数：
new_data = data.sample(frac=1)  # 打乱数据，没有这一步也可以
g,cost = mb_gradient_descent(new_data,theta,alpha,mb_size)

# g的值为matrix([[0.02717606, 3.3047963 ]])

绘制代价函数的值与迭代次数的关系图像：

fig, axes = plt.subplots()
axes.plot(np.arange(len(cost)), cost, 'r')
axes.set_xlabel('iters')
axes.set_ylabel('cost')
axes.set_title('cost vs. iters')
fig.savefig('p2.png')

本文所用的数据集中一共有5106条数据。在小批量梯度下降算法中，笔者采用的mini_batch_size(即算法中的mb_size参数)为50。从上图中我们可以看到在仅仅迭代了20次后，代价函数的值已经开始在某个值上下进行小范围波动。经过大约100次迭代后，得到的theta参数值为matrix([[0.02717606, 3.3047963 ]])。而用正规方程求出的theta参数的精确值为matrix([[-2.34868067],[ 3.31348565]])，可以看出两者差别在一定程度上是可以接受的。关于用正规方程求解线性回归参数可以参考：https://blog.csdn.net/qq_41080850/article/details/85292769、https://blog.csdn.net/qq_41080850/article/details/85159645。

根据前文计算出的theta参数值，绘制原始数据的线性拟合图：

x = np.linspace(data.Area.min(),data.Area.max(),100)
f = g[0,0] + g[0,1]*x

fig,axes = plt.subplots()
axes.plot(x,f,'r',label='Fitted')
axes.scatter(x=data.Area,y=data.Price,label='Trainning data')
axes.legend(loc='best')
axes.set(xlabel='Area',ylabel='Price',title='Area vs. Price')
fig.savefig('p3.png')

参考：Andrew Ng机器学习公开课

PS：本文为博主原创文章，转载请注明出处。

小批量梯度下降算法的Python实现

猜你喜欢