机器学习中的隐马尔科夫模型（HMM）详解

前导性推荐阅读资料：

欢迎关注白马负金羁的博客 http://blog.csdn.net/baimafujinji，为保证公式、图表得以正确显示，强烈建议你从该地址上查看原版博文。本博客主要关注方向包括：数字图像处理、算法设计与分析、数据结构、机器学习、数据挖掘、统计分析方法、自然语言处理。

引言

在之前介绍贝叶斯网络的博文中，我们已经讨论过概率图模型（PGM）的概念了。Russell等在文献【1】中指出：“在统计学中，图模型这个术语指包含贝叶斯网络在内的比较宽泛的一类数据结构。” 维基百科中更准确地给出了PGM的定义：“A graphical model or probabilistic graphical model is a probabilistic model for which a graph expresses the conditional dependence structure between random variables. ” 如果你已经掌握了贝叶斯网络，那么你一定不会对PGM的概念感到陌生。本文将要向你介绍另外一种类型的PGM，即隐马尔可夫模型（HMM，Hidden Markov Model）。更准确地说，HMM是一种特殊的贝叶斯网络。

一些必备的数学知识

随机过程（Stochastic Process）是一连串随机事件动态关系的定量描述。如果用更为严谨的数学语言来描述，则有：设对每一个 t∈T，X(t,w) 是一个随机变量，称随机变量族 XT={X(t,w),t∈T} 为一随机过程（或随机函数），其中 T∈R 称为指标集，R 是实数集。w∈Ω，Ω为样本空间。用映射来表示XT，

X (t, w) ： T \times Ω \to R

即 X(⋅,⋅)X(⋅,⋅) 是定义在 T×ΩT×Ω 上的二元单值函数。其中 T×ΩT×Ω 表示 TT 和 ΩΩ 的笛卡尔积。

参数 t∈T 一般表示时间。当 T 取可列集时，通常称 XT 为随机序列。XT (t∈T) 可能取值的全体集合称为状态空间，状态空间中的元素称为状态。

马尔科夫过程（Markov Process）是本文中我们所要关注的一种随机过程。粗略地说，一个随机过程，若已知现在的 t 状态 Xt, 那么将来状态 Xu (u>t) 取值（或取某些状态）的概率与过去的状态 Xs (s>t) 取值无关；或者更简单地说，已知现在、将来与过去无关（条件独立），则称此过程为马尔科夫过程。

同样，我们给出一个精确的数学定义如下：若随机过程{Xt,t∈T}对任意 t1<t2<…<tn<t，xi，1≤i≤n 及 A 是 R 的子集，总有

P {X t \in A | X t 1 = x 1, X t 2 = x 2, \dots, X t n = x n} = P {X t \in A | X t n = x n}

则称此过程为 马尔科夫过程 。称 P(s,x;t,A)=P{Xt∈A|Xs=x}P(s,x;t,A)=P{Xt∈A|Xs=x} ， s>ts>t , 为转移概率函数。 XtXt 的全体取值构成集合 SS 就是状态空间。对于马尔可夫过程 XT={Xt,t∈T}XT={Xt,t∈T} ，当 S={1,2,3,⋯}S={1,2,3,⋯} 为可列无限集或有限集时，通常称为马尔科夫链（Markov Chain）。

从时间角度考虑不确定性

在前面给出的贝叶斯网络例子中，每一个随机变量都有唯一的一个固定取值。当我们观察到一个结果或状态时（例如Mary给你打电话），我们的任务是据此推断此时发生地震的概率有多大。而在此过程中，Mary是否给你打过电话这个状态并不会改变，而地震是否已经发生也不会改变。这就说明，我们其实是在一个静态的世界中来进行推理的。

但是我们现在要研究的HMM，其本质则是基于一种动态的情况来进行推理，或者说是根据历史来进行推理。假设要为一个高血压病人提供治疗方案，医生每天为他量一次血压，并根据这个血压的测量值调配用药的剂量。显然，一个人当前的血压情况是跟他过去一段时间里的身体情况、治疗方案，饮食起居等多种因素息息相关的，而当前的血压测量值相等于是对他当时身体情况的一个“估计”，而医生当天开具的处方应该是基于当前血压测量值及过往一段时间里病人的多种情况综合考虑后的结果。为了根据历史情况评价当前状态，并且预测治疗方案的结果，我们就必须对这些动态因素建立数学模型。

而隐马尔科夫模型就是解决这类问题时最常用的一种数学模型，简单来说，HMM是用单一离散随机变量描述过程状态的时序概率模型。HMM的基本模型可用下图来表示，其中涂有阴影的圆圈 yt−2,yt−1,yt 相当于是观测变量，空白圆圈 xt−2,xt−1,xt 相当于是隐变量。回到刚刚提及的高血压治疗的例子，你所观测到的状态（例如血压计的读数）相当于是对其真实状态（即病人的身体情况）的一种估计（因为观测的过程中必然存在噪声），用数学语言来表述就是P(yt|xt)，这就是模型中的测量模型或测量概率（Measurement Probability）。另外一方面，当前的（真实）状态（即病人的实际身体状况）应该与其上一个观测状态相关，即存在这样的一个分布P(xt|xt−1)，这就是模型中的转移模型或转移概率（Transition Probability）。当然，HMM中隐变量必须都是离散的，观测变量并无特殊要求。

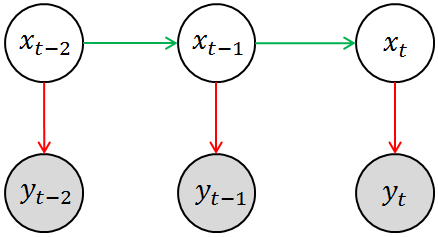
注意这里我们其实使用了马尔科夫假设： 即当前状态只依赖于过去的有限的已出现的历史 。我们前面所采用的描述是：“已知现在的 tt 状态 XtXt , 那么将来状态 Xu(u>t)Xu(u>t) 取值（或取某些状态）的概率与过去的状态 Xs(s>t)Xs(s>t) 取值无关”。两种表述略有差异，但显然本质上是一致的。而且更准确的说，在HMM中，我们认为当前状态紧跟上一个时刻的状态有关，即前面所谓的“有限的已出现的历史”就是指上一个状态。用数学语言来表述就是

P (x t | x t - 1, x t - 2, \dots, x 1) = P (x t | x t - 1)

如果读者已经阅读过本文最开始列出的两篇文章，那么你应该已经意识到，这其实是PGM三种基本的结构单元中的最后一种情况，即条件独立型的结构单元。

再结合HMM的基本图模型（即上图），我们就会得出HMM模型中的两个重要概率的表达式：

离散的转移概率（Transition Probability）“
$P (x t | x t - 1, x t - 2, \dots, x 1, y 1, \dots, y t - 1) = P (x t | x t - 1)$
连续（或离散）的测量概率（Measurement Probability）
$P (y t | x t, x t - 1, \dots, x 1, y 1, \dots, y t - 1) = P (y t | x t)$

一个简单的例子

现在我们已经了解了HMM的基本结构，接下来不妨通过一个实际的例子来考察一下，HMM的转移概率和测量概率到底是什么样的。下图给出了一个用于表示股市动态的概率图模型，更具体的说这是一个马尔科夫模型（Markov Model），因为该图并未涉及隐状态信息。根据之前（以贝叶斯网络为例的）PGM学习，读者应该可以看懂改图所要展示的信息。例如，标记为 1 的圆圈表示的是当前股市正处于牛市，由此出发引出一条指向自身，权值为0.6的箭头，这表示股市（下一时刻）继续为牛市的概率为0.6；由标记为 1 的圆圈引出的一条指向标记为 2 的圆圈的箭头，其权值为0.2，这表示股市（下一时刻）转入熊市的概率是0.2；最后，由标记为 1 的圆圈引出的一条指向标记为 3 的圆圈的箭头，其权值为0.2，这表示股市（下一时刻）保持不变的概率是0.2。显然，从同一状态引出的所有概率之和必须等于1。

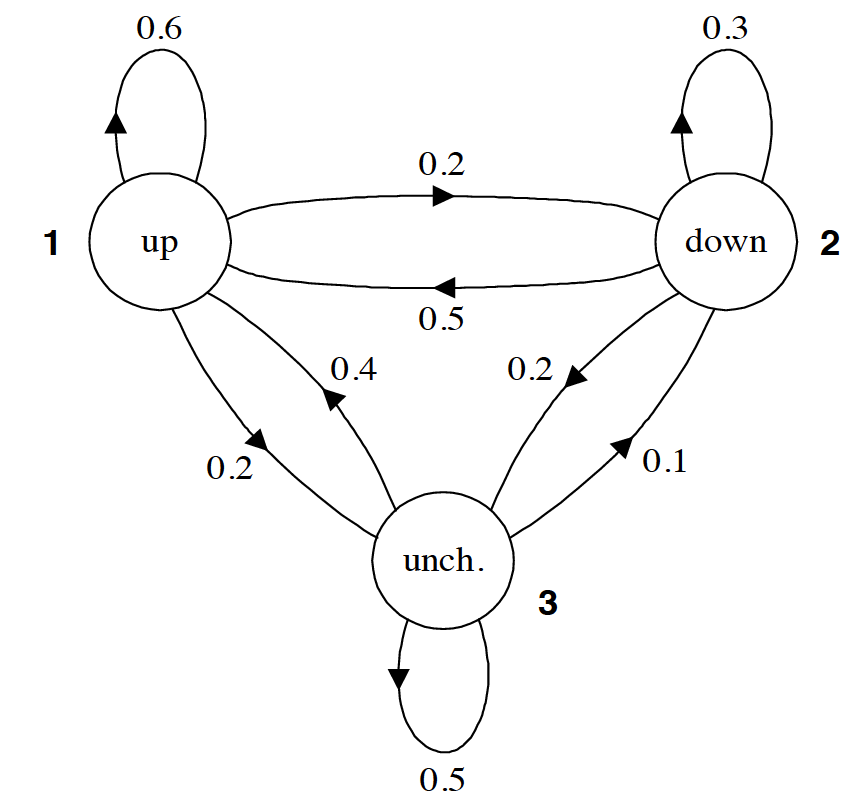
所以马尔科夫模型中的各个箭头代表的就是 状态之间相互转化的概率 。而且，通常我们会把马尔科夫模型中所有的转移概率写成一个矩阵的形式，例如针对本题而已，则有

A = ⎡ ⎣ ⎢ 0.6 0.5 0.4 0.2 0.3 0.1 0.2 0.2 0.5 ⎤ ⎦ ⎥

如果马尔科夫模型中有 k 个状态，那么对应的状态转移矩阵的大小就是 k×k。其中第 m 行，第 n 列所给出的值就是 P(xt=n|xt−1=m)。也就给定状态 m 的情况下，下一时刻转换到状态 n 的概率。例如，第2行，第1列的值为 0.5，它的意思就是如果当前状态是标记为 2 的圆圈（熊市），那么下一时刻转向标记为 1 的圆圈（牛市）的概率是 0.5。而且，矩阵中，每一行的所有值之和必须等于1。

至此，我们已经知道可以用一个矩阵 A 来代表 P(xt|xt−1)，那又该如何表示 P(yt|xt) 呢？当然，由于P(yt|xt) 可能是连续的，也可能是离散的，所以不能一言以蔽之。为了简化，我们当前先仅考虑离散的情况。当引入 P(yt|xt) 之后，我们才真正得到了一个隐马尔科夫模型，上面我们所说的标记为1、2 和 3 的（分别代表牛市、熊市和平稳）三个状态现在就变成了隐状态。当隐状态给定后，股市的表现可能有 l=3 种情况，即当前股市只能处于“上涨”，“下跌”，或者“不变”三种状态之一。完整的HMM如下图所示。

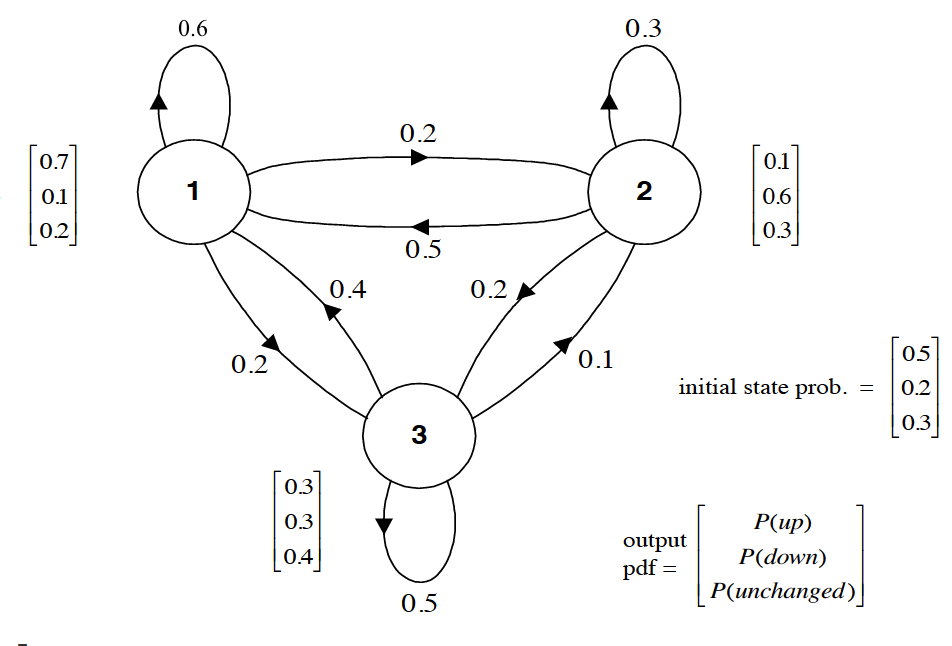
易知，（当测量概率是离散的情况下），HMM中的 P(yt|xt)P(yt|xt) 也可以用一个矩阵 BB 来表示。并且 BB 的大小是 k×lk×l 。对于当前这个例子而言，我们有

B = ⎡ ⎣ ⎢ 0.7 0.1 0.3 0.1 0.6 0.3 0.2 0.3 0.4 ⎤ ⎦ ⎥

其中第 1 行，第 1 列，就表示 P(yt=1 | xt=1)P(yt=1 | xt=1) ，也就是我们已知当前正处于牛市，股票上升的概率为0.7；同理，第 1 行，第 2 列，就表示 P(yt=2 | xt=1)P(yt=2 | xt=1) ，也就是我们已知当前正处于牛市，股票下跌的概率为0.1。

再次强调，只有当测量概率是离散的情况下，我们才能用一个矩阵来表示P(yt|xt) 。对于连续的情况，比如我们认为观测变量的取值符合高斯分布，也即是概率 P(yt|xt) 的分布符合高斯分布，那么应该有多少个高斯分布呢？显然有多少个隐状态（例如 k 个），就应该有多少个高斯分布。那么矩阵 B 就应该变成了由 k 个高斯分布的参数，即 σ1,μ1,σ2,μ2,⋯,σk,μk，组成的一个集合。

之前的文章里我们谈过，人类学习的任务是从资料中获得知识，而机器学习的任务是让计算机从数据中获得模型。那模型又是什么呢？回想一下机器学习中比较基础的线性回归模型 y=∑iwixi，我们最终是希望计算机能够从已有的数据中或者一组最合适的参数 wi，因为一旦wi 被确定，那么线性回归的模型也就确定了。同样，面对HMM，我们最终的目的也是要获得能够用来确定（数学）模型的各个参数。通过前面的讨论，我们也知道了定义一个HMM，应该包括矩阵 A 和矩阵 B （如果测量概率是离散情况的话），那只有这些参数能够足以定义个HMM呢？

要回答这个问题，我们不妨来思考一下这样一个问题。假如我们现在已经得到了矩阵 A 和矩阵 B，那么我们能否求出下面这个序列的概率 P(y1=上涨,y2=上涨,y3=下跌)。注意对于这样一个序列，我们并不知道隐状态的情况，所以采用贝叶斯网络中曾经用过的方法，设法把隐状态加进去，在通过积分的方法将未知的隐状态积分积掉。于是有

P (y 1, y 2, y 3) = \sum x 1 k \sum x 2 k \sum x 3 k P (y 1, y 2, y 3, x 1, x 2, x 3) = \sum x 1 k \sum x 2 k \sum x 3 k P (y 3 | y 1, y 2, x 1, x 2, x 3) \times P (y 1, y 2, x 1, x 2, x 3)

这里就可以运用马尔科夫假设进行简化，所以上式就变成了

= \sum x 1 k \sum x 2 k \sum x 3 k P (y 3 | x 3) \times P (y 1, y 2, x 1, x 2, x 3) = \sum x 1 k \sum x 2 k \sum x 3 k P (y 3 | x 3) \times P (x 3 | y 1, y 2, x 1, x 2) \times P (y 1, y 2, x 1, x 2) = \sum x 1 k \sum x 2 k \sum x 3 k P (y 3 | x 3) \times P (x 3 | x 2) \times P (y 1, y 2, x 1, x 2) = \sum x 1 k \sum x 2 k \sum x 3 k P (y 3 | x 3) \times P (x 3 | x 2) \times P (y 2 | x 2) \times P (x 2 | x 1) \times P (y 1 | x 1) \times P (x 1)

到这里，我们就很容易发现，上面这个式子中，还有一个未知量，那就是PGM的初始状态，我们将其记为 ππ 。

于是我们知道，要确定一个HMM模型，我们需要知道三个参数，我们将其记作 λ(A, B, π)。

在后续的文章中我们会进一步探讨，如何让机器能够自己学到上面这些参数，以及HMM的具体应用。

参考文献

[1] Stuart Russell and Peter Norvig. Artificial Intelligence: A Modern Approach. 3rd Edition.

[2] 徐伟，赵选民，师义民，秦超英，概率论与数理统计（第2版），西北工业大学出版社

[3] 同时推荐悉尼科大徐亦达博士的机器学习公开课中关于HMM的部分

[4] 关于HMM在NLP中的应用，可以参考Speech and Language Processing. Daniel Jurafsky & James H. Martin, 3rd. Chapter 6