机器学习----纯手撸线性回归代码

什么是线性回归？

线性回归是利用函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析, 简单来说线性回归其实是试图找到自变量与因变量之间的关系

比如房子的面积和价格：

房子的面积越大，房子的价格就越高

假设房子的面积和价格符合方程y = mx + b

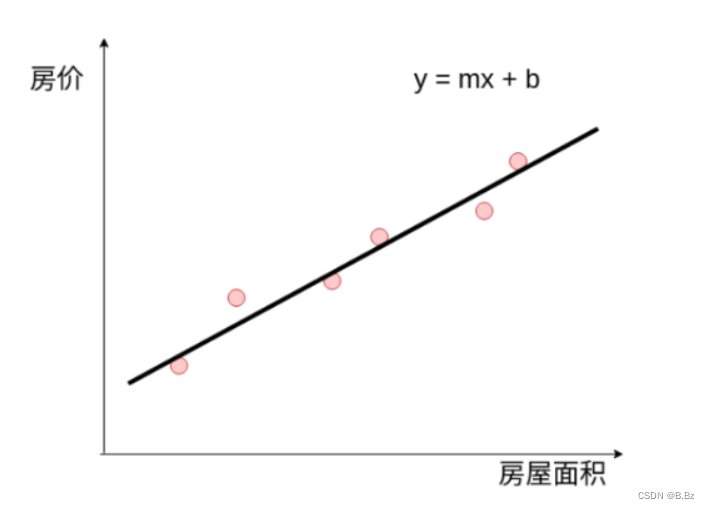
在这里插入图片描述

准备房子面积和价格的数据

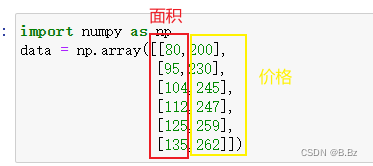
在这里插入图片描述

import numpy as np
data = np.array([[80,200],
                 [95,230],
                 [104,245],
                 [112,247],
                 [125,259],
                 [135,262]])

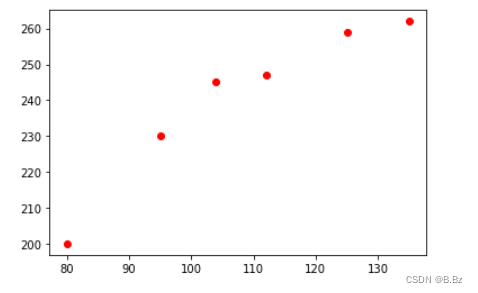
在这里插入图片描述
要预测140平方的房子价格，根据上面已有的数据，求解出m和b的最优值，就可以预测出140平方的房子价格。

MSE(均方误差)

均方误差是各数据偏离真实值的差值的平方和的平均数

$M S E$ $=$ $\over {N}$ $\displaystyle \sum^{N}_{i=1}\left(预测值-真实值\right)^2$

只看一个MSE的结果是没有意义的
根据不同的m和b的值计算出的均方误差来进行对比，符合方程式走向的数据，MSE的值越小说明越接近真实值。
在预测的次数相同时计算平均数保留和去掉的关系不大

简化公式为：

$M S E$ $=\displaystyle \sum^{N}_{i=1}\left(预测值-真实值\right)^2$

导数

导数是函数的局部性质。
一个函数在某一点的导数描述了这个函数在这一点附近的变化率。
函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。
导数的本质是通过极限的概念对函数进行局部的线性逼近。
举例： 在运动学中，物体的位移对于时间的导数就是物体的瞬时速度, 速度的导数就是加速度

原函数：

x = np.linspace(-100,100,100)
y = x**2 + 5
plt.figure()
plt.scatter(x,y,c="b")
plt.show()

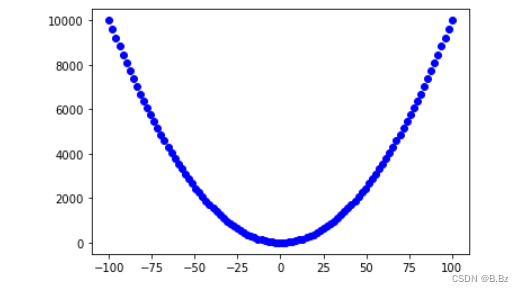
在这里插入图片描述

导函数：

x = np.linspace(-100,100,100)
y = 2*x
plt.figure()
plt.scatter(x,y,c="r")
plt.show()

在这里插入图片描述

结合导数的原理总结规律：

导数值为负 x增大 mse下降
导数值为正 x减小 mse下降
导数值负的越大 x增加一点 mse就会下降很多
导数值正的越大 x减少一点 mse就会下降很多

所以：

坡度越陡峭，步伐应该小一点（学习率小一点）
反之，学习率应该大一点，加速到达底部的速度。

梯度下降

梯度是一个向量，表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大。
梯度是朝着函数增大的方向去找最大值，我们要寻找mse最小的值，所以是求梯度最小值（朝着函数下降的方向），是为梯度下降。

把设定好的`y=mx + b`带入到公式：

$M S E$ $=\displaystyle \sum^{N}_{i=1}\left(m\times 面积i + b-真实值i\right)^2$

求出公式内两个未知数的偏导数：

b：
$\over {\Delta b}$ $=\displaystyle 2 \times\sum^{N}_{i=1}\left(m\times xi + b-真实值i\right)$

m：

$\over {\Delta m}$ $=\displaystyle 2 \times\sum^{N}_{i=1}\left(m\times xi + b-真实值i\right) \times x$

`梯度下降步骤:`

随便初始化一个值为m、b
计算m、b对应的mse斜率（偏导数）
如果mse斜率大，根据偏导数的值取修改m、b的值
mse值越大，b和m的修改值越大。mse斜率为正，b和m需要减少；mse斜率为负，b和m需要增加
选取一个很小的值为学习率，每一次更新b和m的值之前和学习率相乘减小改变力度，可以理解为梯度下降的步伐，学习率越大迈的步子越大，反之则越小。
根据mse是否接近稳定，一直去修改b和m的值和学习率相乘直到mse的斜率接近于0

# 定义m和b的初始值
m = 1
b = 1
# 定义学习率，小一点，如果太大就有可能一步跨到函数梯度下降的反方向
learningrate = 0.00001

def gradient_descent():
	"""
	梯度下降的函数
	"""
    global m,b
    # 每次进入函数重新定义mse和m、b的偏导数  以便多次训练模型
    mse,mslop,bslop = 0,0,0
    # 遍历历史数据
    for x_i,real_i in data:
    	# 均方误差公式 算出均方误差
        mse += (m * x_i + b - real_i)**2
        # 计算出m的偏导数
        mslop += 2*(m*x_i+b - real_i)*x_i
        # 计算出b的偏导数
        bslop += 2*(m*x_i+b -real_i)
    # 更新m的值  如果偏导数为负值 m - mslop就等于加值
    # 如果偏导数为正值m - mslop就会减值，mse一直会朝着函数最小值前进
    # 乘以学习率是为了让步伐小一点，避免一下跨步很大
    m = m - mslop*learningrate
    b = b - bslop*learningrate
    return m,b,mse

# 定义计算后的最优m和b的值
final_m,final_b,final_mse=0,0,0
# 训练3百万次
for i in range(3000000):
    final_m,final_b,final_mse = gradient_descent()
    if i%100000 == 0:
        print("m={},b={},mse={}".format(final_m,final_b,final_mse))

查看结果发现：
在这里插入图片描述

当mse收敛到一定程度不再怎么收敛，就说明找到了参数m和b的最优解

画图查看模型精度，评估：

# 真实房子数据
plt.scatter(data[:,0],data[:,1],c='pink')
# 画出回归完的模型
X = np.linspace(50,200,200)
Y = final_m * X + final_b
plt.plot(X,Y,c='r')

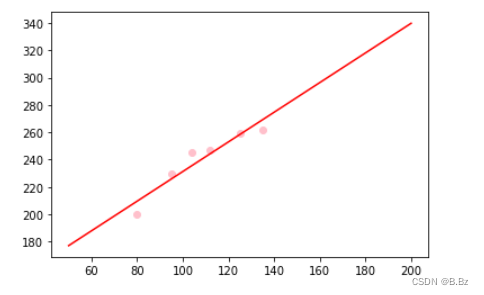
在这里插入图片描述

此时使用m和b的值来预测140平方米的房子需要多少钱：

y = final_m * 140 + final_b
print(f'140平米的房子预测需要：{
      
      y}万元')

在这里插入图片描述