贪心算法基本概念:
所谓贪心算法是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,它所做出的仅仅是在某种意义上的局部最优解。
贪心算法不是对所有问题都能得到整体最优解,关键是贪心策略的选择
贪心算法一般步骤
建立数学模型来描述问题,明确什么是最优解。
把求解的问题分成若干个子问题。
对每个子问题求解,得到子问题的局部最优解。
把子问题的解局部最优解合成原来解问题的一个解。
例子:
假设有如下课程表,由于有些课的上课时间有冲突,没
法让这些课都在这间教室上。
你希望将尽可能多的安排课程。
如何选出尽可能多且时间不冲突的课程呢?
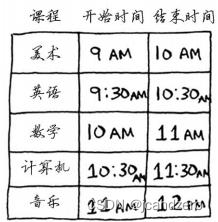
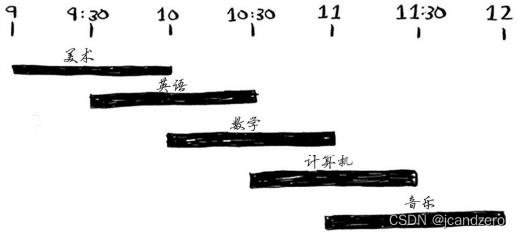
这个问题似乎很难。
实际上,算法可能简单得让你大吃一惊。具体做法如下
(1) 选出结束最早的课,就是要在这间教室上的第一堂课。
(2) 接下来,必须选择第一堂课结束后才开始的课。同样,你选择结束最早的课,这将是要在这间教室上的第二堂课。
问题举例
我们发现这个算法很容易、很显而易见,这正是贪婪算法的优点——简单易行!
贪婪算法很简单:每步都采取最优的做法。在这个示例中,你每次都选择结束最早的课,即每步都选择局部最优解,最终得到的就是全局最优解。
对于这个调度问题,上述简单算法找到的就是最优解!
当然,贪婪算法并非在任何情况下都行之有效,但它易于实现!
背包问题。
有一个背包,最多能承载150斤的重量,现在有7个物
品,重量分别为[35, 30, 60, 50, 40, 10, 25],它们的价
值分别为[10, 40, 30, 50, 35, 40, 30]。
如果是你的话,应该如何选择才能使得我们的背包背走
最多价值的物品?
也就是说:每一个物品,要么选择,要么放弃,这就是著名0-1背包问题。
问题举例——背包问题
按照之前提到的步骤走:
(1)明确到底什么是最优解?
在重量限制范围内,价值最大的选择,就是最优解。
(2)把求解的问题分成若干个子问题,再用小本本记下来!
其实对于子问题,有很多定义方法,这里我们先选择最
直接的方式来定义:认为每次都尽量选择当前价值最高
的物品,这就是局部最优解。
(3)分别求出子问题的最优解再堆叠出全局最优解。
按照制订的规则(价值)进行计算,顺序是:4 2 6 5 。
最终的总重量是:130。
最终的总价值是:165。
问题举例——背包问题
前面是一种方法,其实定义子问题最优解还有不同的定
义方法。
刚才我们使用价值最高作为标准,也可以将当前物品中
重量最小的作为最优选择。
按照制订的规则(重量)进行计算,顺序是:6 7 2 1 5 。
最终的总重量是:140。
最终的总价值是:155。
可以看到,重量优先是没有价值优先的策略更好。
问题举例——背包问题
其实还可以这样定义:每次都选择“价值密度”最高的
物品。
价值密度就是指单位重量的价值。
按照制订的规则(价值密度)进行计算,顺序是:6 2 7
4 1。
最终的总重量是:150。
最终的总价值是:170。
可以看到,价值密度这个策略比之前的价值策略和重量
策略都要好。
问题举例
练习1
你在一家家具公司工作,需要将家具发往全国各地,为此你需要将箱子装上卡车。每个箱子的尺寸各不相同,你需要尽可能利用每辆卡车的空间,为此你将如何选择要装上卡车的箱子呢?请设计一种贪婪算法。使用这种算法能得到最优解吗?
问题举例
练习2
你要去欧洲旅行,总行程为7天。对于每个旅游胜地,你都给它分配一个价值——表示你有多想去那里看看,并估算出需要多长时间。你如何将这次旅行的价值最大化?请设计一种贪婪算法。使用这种算法能得到最优解吗?
练习1一种贪婪策略是,选择可装入卡车剩余空间内的最大箱子,并重复这个过程,直到不能再装入箱子为止。使用这种算法不能得到最优解。
练习2不断地挑选可在余下的时间内完成的价值最大的活动,直到余下的时间不够完成任何活动为止。使用这种算法不能得到最优解。
问题举例——集合覆盖问题
假设你办了个广播节目,要让全美50个州的听众都收听得到。为此,你需要决定在哪些广播台播出。在每个广播台播出都需要支付费用,因此你力图在尽可能少的广播台播出。现有广播台名单如下
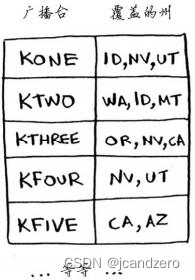
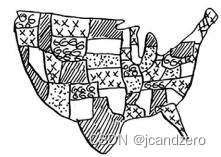
每个广播台都覆盖特定的区域,不同广播台的覆盖区域可能重叠。
如何找出覆盖全美50个州的最小广播台集合呢?

问题举例——集合覆盖问题
具体方法如下。
a. 列出每个可能的广播台集合,这被称为幂集(power set)。可能的子集有2的n次方个。
b. 在这些集合中,选出覆盖全美50个州的最小集合。
问题是计算每个可能的广播台子集需要很长时间。由于可能的集合有个,因此运行时间为O(
)。
如果广播台不多,只有5~10个,这是可行的。但如果广播台很多,结果将如何呢?
随着广播台的增多,需要的时间将激增。假设你每秒可计算10个子集,所需的时间将如上。
没有任何算法可以足够快地解决这个问题!怎么办呢?
贪心算法可化解危机!使用下面的贪心算法可得到非常接近的解。
选出这样一个广播台,即它覆盖了最多的未覆盖州。即便这个广播台覆盖了一些已覆盖的州,也没有关系。
重复第一步,直到覆盖了所有的州。
这是一种近似算法(approximation algorithm)。
在获得精确解需要的时间太长时,可使用近似算法。判断近似算法优劣的标准如下:
速度有多快;
得到的近似解与最优解的接近程度。
贪婪算法是不错的选择,它们不仅简单,而且通常运行速度很快。在这个例子中,贪婪算法的运行时间为O(n2),其中n为广播台数量。
集合类似于列表,只是同样的元素只能出现一次,即集合不能包含重复的元素。
例如,假设你有如下列表。
将其转换为集合。在这个集合中,1、2和3都只出现一次。

问题举例——集合覆盖问题
还需要有可供选择的广播台清单,我选择使用散列表来表示它。
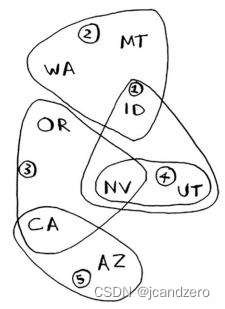
其中的键为广播台的名称,值为广播台覆盖的州。在该示例中,广播台kone覆盖了爱达荷州、内达华州和犹他州。所有的值都是集合。
最后,需要使用一个集合来存储最终选择的广播台。
# 需要覆盖广播台的州
states_needed = set(["mt", "wa", "or", "id", "nv", "ut", "ca", "az"])
#可供选择的广播台可覆盖的州
stations = {}
stations["kone"] = set(["id", "nv", "ut"])
stations["ktwo"] = set(["wa", "id", "mt"])
stations["kthree"] = set(["or", "nv", "ca"])
stations["kfour"] = set(["nv", "ut"])
stations["kfive"] = set(["ca", "az"])
#存储最终选择的广播台
final_stations = set()
while states_needed: ##states_=needed当中还存在有州没有完成覆盖
#遍历所有的广播台,从中选择覆盖了最多的未覆盖州的广播台,存储在best_station中
best_station = None
#储存该广播台覆盖的所有未覆盖的州
states_covered = set()
for station, states_for_station in stations.items():
#同时出现在states_needed和states_for_station中的州:当前广播台覆盖的一系列还未覆盖的州
covered = states_needed & states_for_station
if len(covered) > len(states_covered):
best_station = station
states_covered = covered
states_needed -= states_covered
final_stations.add(best_station)
print(final_stations)
选择的广播台可能是2、3、4和5,而不是预期的1、2、3和5。下面来比较一下贪婪算法和精确算法的运行时间

问题举例——活动选择问题
假设有n 个活动,这些活动要占用同一片场地,而场地在某时刻只能供一个活动使用。
每一个活动都有一个开始时间Si 和结束时间Fi (题目中时间以整数表示)表示活动在[Si, fi) 区间占用场地。
(注意:左开右闭)
问:安排哪些活动能够使该场地举办的活动的个数最多?
贪心结论:最先结束的活动一定是最优解的一部分。
证明:假设a 是所有活动中最先结束的活动,b是最优解中最先结束的活动。
如果a=b,结论成立
如果a!=b,则b 的结束时间一定晚于a 的结束时间,则此时用a 替换掉最优解中的b ,a 一定不与最优解中的其他活动时间重叠,因此替换后的解也是最优解
NP完全问题
旅行商问题详解
NP 完全问题
旅行商问题可以用贪心算法求解吗?
我们用一个简单的例子表示贪心算法求解旅行商问题的步骤。使用直角坐标系来表示各个城市的位置,其中起
点为(0,0)。
贪心算法:从起点(0, 0)出发,选择最近的点;再从该点出发,选择最近的点;重复执行该步骤,直到没有点时返回起点。
NP 完全问题
随便选择出发城市,然后每次选择要去的下一个城市时,都选择还没去的最近的城市。假设旅行商从马林出发。
总旅程为71英里。这条路径可能不是最短的,但也相当短了。
NP 完全问题
NP完全问题(NP-C问题),是世界七大数学难题之一
NP就是Non-deterministic Polynomial的问题,也即
是多项式复杂程度的非确定性问题。
如果任何一个NP问题都能通过一个多项式时间算法转换
为某个NP问题,那么这个NP问题就称为NP完全问题
(Non-deterministic Polynomial complete
problem)。