每日一题·夏季 [Acwing 3565] 完美矩阵

原题链接：Acwing 3565 完美矩阵

题目

如果一个矩阵能够满足所有的行和列都是回文序列，则称这个矩阵为一个完美矩阵。

一个整数序列 $a_1,a_2,\dots ,a_k$，如果满足对于任何整数 i（$1\le i\le k$），等式 $a_i=a_k-i+1$ 均成立，则这个序列是一个回文序列。

给定一个 n×m 的矩阵 a，每次操作可以将矩阵中的某个元素加一或减一，请问最少经过多少次操作后，可以将矩阵 a 变为一个完美矩阵？

输入格式

第一行包含整数 T，表示共有 T 组测试数据。

每组数据第一行包含整数 n 和 m，表示矩阵的大小。

接下来 n 行，每行包含 m 个整数 $a_{ij}$，表示矩阵中的元素。

输出格式

每组数据输出一行，一个答案，表示最少操作次数。

数据范围

$1\le T\le 10$,
$1\le n,m\le 100$,
$0\le a_{ij}\le 10^9$

输入样例：

2
4 2
4 2
2 4
4 2
2 4
3 4
1 2 3 4
5 6 7 8
9 10 11 18

输出样例：

8
42

样例解释

第一组数据可以通过 8 步操作得到以下矩阵：

2 2
4 4
4 4
2 2

第二组数据可以通过 42 步操作得到以下矩阵：

扫描二维码关注公众号，回复： 14773810 查看本文章

5 6 6 5
6 6 6 6
5 6 6 5

思路：

对于一个完美矩阵，要是回文序列，且要求横着竖着都是这样，实质上就是要求每一个如下对称得到的四元组都相同。

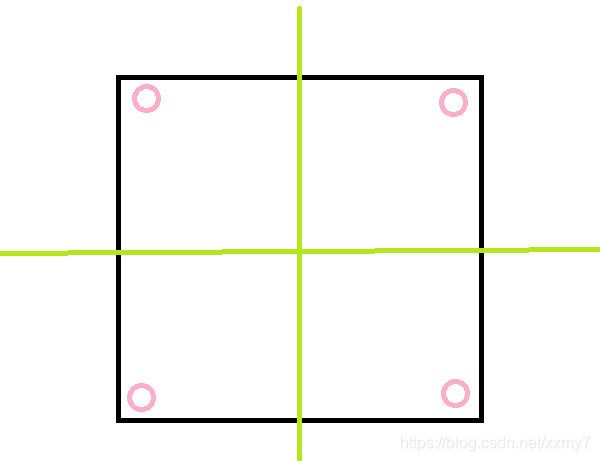
所以只需要枚举所有左上方块内的点，获得所有的四元组，然后让每个四元组都变到相等，且步数最少就可以使得整体步数最少了。
对于$a,b,c,d$四个数，要让他们变成一样且步数最少。
即求$|a-x|+|b-x|+|c-x|+|d-x|$最小，根据绝对值不等式可知 $x$ 取 $a,b,c,d$ 的中位数时就是最小的。如果是偶数，取中间两个数之间的任意值都可以。
 
考虑到这个获得的四元组可能只有2个点或者1个点，所以可以通过set存储去重，因为我们获得四元组是通过对称得到的。

偶数就枚举到中线的前面一个，奇数就枚举到了中线的那一行（或者那一列）

代码

#include <iostream>
#include <cstring>
#include <algorithm>
#include <set>
#include <vector>

#define x first
#define y second

using namespace std;

typedef long long LL;
typedef pair<int, int> PII;

const int N = 110;

int n, m;
int w[N][N];

LL calc(set<PII> S)
{
    
    
    vector<int> q;
    for (auto& p: S) q.push_back(w[p.x][p.y]);
    sort(q.begin(), q.end());
    LL res = 0;
    for (int i = 0; i < q.size(); i ++ )
        res += abs(q[i] - q[q.size() / 2]);
    return res;
}

int main()
{
    
    
    int T;
    scanf("%d", &T);
    while (T -- )
    {
    
    
        scanf("%d%d", &n, &m);
        for (int i = 0; i < n; i ++ )
            for (int j = 0; j < m; j ++ )
                scanf("%d", &w[i][j]);

        LL res = 0;
        for (int i = 0; i <= n - 1 - i; i ++ )
            for (int j = 0; j <= m - 1 - j; j ++ )
                res += calc({
    
    {
    
    i, j},{
    
    i, m - 1 - j},{
    
    n - 1 - i, j},{
    
    n - 1 - i, m - 1 - j}});
        printf("%lld\n", res);
    }
    return 0;
}