Pca,Kpca,TSNE降维非线性数据的效果展示与理论解释
前言
本文主要介绍运用机器学习中常见的降维技术对数据提取主成分后并观察降维效果。我们将会利用随机数据集并结合不同降维技术来比较它们之间的效果。降维技术可以说非常常见的有Pca、Kpca、TSNE、LDA、NMF、神经网络自编码技术等,也是各有各的特点,比较深入且工业上不怎么通用的有密度敏感鲁棒模糊核主成分分析算法(DRF-Kpca)等等,有兴趣的朋友可以查查此类相关文章。这篇文章主要先介绍Pca、Kpca、TSNE这三种方法。

岁月如云,匪我思存,写作不易,望路过的朋友们点赞收藏加关注哈,在此表示感谢!
一:几类降维技术的介绍
由于本篇是应用篇,主要会设计算法介绍与流程,以及实验结果,过多的降维原理不会细致展开。
- PCA概括
我们主要引用一下百度百科的简洁明了的概括内容。
PCA(principal components analysis)即主成分分析技术,又称主分量分析。主成分分析也称主分量分析,旨在利用降维的思想,把多指标转化为少数几个综合指标。
在统计学中,主成分分析PCA是一种简化数据集的技术。它是一个线性变换。这个变换把数据变换到一个新的坐标系统中,使得任何数据投影的第一大方差在第一个坐标(称为第一主成分)上,第二大方差在第二个坐标(第二主成分)上,依次类推。主成分分析经常用于减少数据集的维数,同时保持数据集的对方差贡献最大的特征。这是通过保留低阶主成分,忽略高阶主成分做到的。这样低阶成分往往能够保留住数据的最重要方面。但是,这也不是一定的,要视具体应用而定。
- Kpca概括
常见核函数的介绍
核函数 k k k 简单来说是通过内积运算把低维数据映射到高维数据,即 k ( x , y ) = < φ ( x ) , φ ( y ) > k(x,y)=<\varphi(x),\varphi(y)> k(x,y)=<φ(x),φ(y)> ,其中 x , y x,y x,y 是低维的输入向量, φ \varphi φ 为低维到高维的映射, < ⋅ , ⋅ > <\cdot,\cdot> <⋅,⋅> 为内积运算。通过升维操作,我们可以很好解决低维的“非线性”问题,最后再降维到我们需要的维度。
现在工程算法上核函数的介绍一般都直接给出个表达式,但是真正基于数学角度触发,核函数很多定义都要加上一些必要的限制,比如“可微、连续、对称、有界、泛函空间”等等(其实很多机器学习(深度学习)算法的真正底层逻辑成立是要很多条件限制才行得通的),由于这里不是存粹数学探讨,我们还是简单概括下。
- 线性核函数
k ( x , y ) = x T y + c , c ≥ 0 k(x,y)=x^Ty+c , c\geq0 k(x,y)=xTy+c,c≥0 ,主要解决线性可分问题。通过表达式我们可以发现,此时的Kpca降维其实跟传统的Pca没啥区别。
- 多项式核函数
k ( x , y ) = ( a x T y + c ) d , a > 0 , c ≥ 0 , d ≥ 1 k(x,y)=(ax^Ty+c)^d , a>0,c\geq0,d\geq1 k(x,y)=(axTy+c)d,a>0,c≥0,d≥1 ,这类核函数比较复杂,可以解决非线性问题。
- 高斯核函数
k ( x , y ) = − γ ∣ ∣ x − y ∣ ∣ 2 , γ ( g a m m a ) = 1 2 σ 2 k(x,y)=-\gamma\left|| x-y \right||^2 , \gamma(gamma)=\frac{1}{2\sigma^2} k(x,y)=−γ∣∣x−y∣∣2,γ(gamma)=2σ21 高斯核函数的运用是比较广泛的,这里我们重点说明下几个重要参数。
∣ ∣ ⋅ , ⋅ ∣ ∣ 2 ||\cdot,\cdot||^2 ∣∣⋅,⋅∣∣2 :两个向量的2-范数运算,
gamma:gamma越大,高斯分布越窄。gamma越小,高斯分布越宽。gamma相当于调整模型的复杂度,gamma值越小模型复杂度越低,gamma值越高,模型复杂度越大。换句话说当gamma非常大,模型容易过拟合,模型对数据比较敏感,因为分布曲线尖端太“狭窄”,每一个样本点几乎占有独立的分布曲线,分布曲线很难再含有其他样本了,反之亦然。但gamma参数是高斯核的“独特”之处,太小体现不出来高斯核特点,太大容易过拟合,所以在实际运用中(如降维、分类等),可以多次实验发现规律并解决问题。
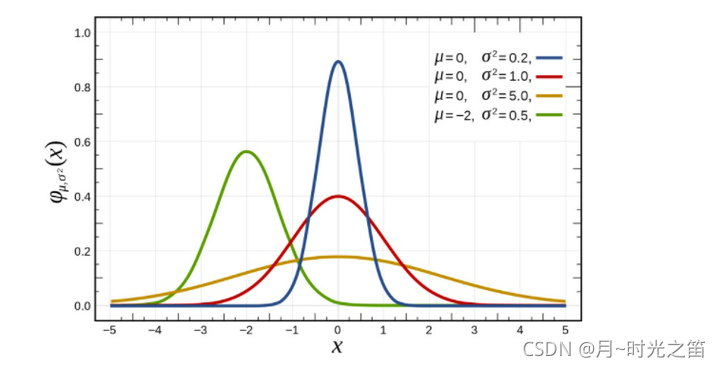
这里我们我们借鉴下百度图库给的图形,因为 σ \sigma σ 跟 γ \gamma γ 属于倒数关系,可以从图1看出 σ \sigma σ 越大, γ \gamma γ 越小,分布越宽。
- TSNE概括
- SNE算法
SNE的思想是基于在高维空间相似的点,或者离得近的点,那么映射到低维希望也是离得近的点,那整个过程就自然实现了降维。我们也有表达“离得近”的公式来描述,那就是高斯条件概率: p j ∣ i ( x ) = e x p ( − ∣ ∣ x i − x j ∣ ∣ 2 / 2 σ i 2 ) ∑ k ≠ i e x p ( − ∣ ∣ x i − x k ∣ ∣ 2 / 2 σ i 2 ) p_{j|i}(x)=\frac{exp(-||x_i-x_j||^2/2\sigma_i^2)}{\sum_{k\ne i}{exp(-||x_i-x_k||^2/2\sigma_i^2)}} pj∣i(x)=∑k=iexp(−∣∣xi−xk∣∣2/2σi2)exp(−∣∣xi−xj∣∣2/2σi2) ,这里点 x j x_j xj 越靠近 x i x_i xi 时,概率越大;同理降维到低维的数据点 y j , y i y_j,y_i yj,yi 的离得远近也是用高斯概率判定。但是,怎么评判两高斯概率分布相似?我们可以用数理统计的 K L KL KL 散度距离(Kullback-Leibler Divergence)判定,最终的目的就是想把 K L KL KL 的值降到最低。
K L KL KL 散度主要基于理论分布拟合真实分布时产生的信息损耗的期望值,我们用公式表示如下:
D K L ( p ∣ ∣ q ) = E [ l o g 2 p ( x ) − l o g 2 ( q ( x ) ) ] D_{KL}(p||q)=E[log_2p(x)-log_2(q(x))] DKL(p∣∣q)=E[log2p(x)−log2(q(x))] ,
那么对应的离散形式可以表示为 :
D K L ( p ∣ ∣ q ) = ∑ i = 1 N p ( x i ) ( l o g 2 p ( x i ) − l o g 2 q ( x i ) ) D_{KL}(p||q)=\sum_{i=1}^{N}{p(x_i)}(log_2p(x_i)-log_2q(x_i)) DKL(p∣∣q)=∑i=1Np(xi)(log2p(xi)−log2q(xi)) ,
对应的连续形式可以表示为:
D K L ( p ∣ ∣ q ) = ∫ − ∞ + ∞ p ( x ) ( l o g 2 p ( x ) − l o g 2 q ( x ) ) d x D_{KL}(p||q)=\int_{-\infty}^{+\infty}p(x)(log_2p(x)-log_2q(x))dx DKL(p∣∣q)=∫−∞+∞p(x)(log2p(x)−log2q(x))dx ,
这里的 p ( x i ) , q ( x i ) p(x_i),q(x_i) p(xi),q(xi) 就是表示真实和理论上的每个随机变量的概率值。
对于SNE算法,那么当 D = p j ∣ i ( x ) D=p_{j|i}(x) D=pj∣i(x) 时,我们希望存在
D ′ = p j ∣ i ( y ) D^{'}=p_{j|i}(y) D′=pj∣i(y)使得
m i n D K L ( D ∣ ∣ D ′ ) = m i n ∑ i j [ D i j l o g 2 D i j D i j ′ − D i j + D i j ′ ] minD_{KL}(D||D^{'})=min\sum_{ij}\left[ {D_{ij}log_2\frac{D_{ij}}{D_{ij}^{'}}-D_{ij}+D_{ij}^{'}} \right] minDKL(D∣∣D′)=min∑ij[Dijlog2Dij′Dij−Dij+Dij′] 存在。
那么每个 y i y_i yi 变量的更新如何处理,这就很自然想到梯度下降算法(这里先不展开叙述了)。
- TSNE是SNE的升级版
升级主要一是在梯度下降算法中的优化,二是在低维空间用T分布代替高斯分布。
- TSNE非常适用于高维数据降维到2维或者3维,进行可视化。
二:主要介绍Kpca的实现步骤
(由于Kpca是Pca的推广,我们略过Pca)
- 我们先获得一个 m × n m\times n m×n 的数据矩阵( m m m 是样本个数, n n n 是每个样本的特征),
- 选择相应核函数计算核矩阵,这里的核矩阵计算主要是根据公式 k ( x i , x j ) = < φ ( x i ) , φ ( x j ) > k(x_i,x_j)=<\varphi(x_i),\varphi(x_j)> k(xi,xj)=<φ(xi),φ(xj)> 计算,其中 0 ≤ i , j ≤ m 0\leq i,j\leq m 0≤i,j≤m ,
- 根据相应公式计算中心化后的核矩阵 k l = k − l ∗ k / m − k ∗ l / m + l ∗ k ∗ l / ( m ∗ m ) kl =k-l\ast k/m-k*l/m+l*k*l/(m*m) kl=k−l∗k/m−k∗l/m+l∗k∗l/(m∗m) , l l l 是 m × m m\times m m×m 的单位矩阵,
- 再计算 k l kl kl 的特征值 λ 1 , λ 2 , . . . λ n \lambda_1,\lambda_2,... \lambda_n λ1,λ2,...λn 和对应的特征向量 ν 1 , ν 2 , . . . ν n \nu_1,\nu_2,...\nu_n ν1,ν2,...νn ,对特征值按照降序排序展开,与此同时特征向量也随之改变,通过斯密特正交化方法得到单位正交化特征向量 α i , α 2 , . . . α n \alpha_i,\alpha_2,...\alpha_n αi,α2,...αn ,确定主成分的个数 p = ∑ i = 1 p λ i / ∑ i = 1 n λ i ≥ β p=\sum_{i=1}^{p}{\lambda_i}/\sum_{i=1}^{n}{\lambda_i}\geq\beta p=∑i=1pλi/∑i=1nλi≥β ,其中 β \beta β 的取值根据实际情况来定,一般不小于0.8,
- 最后我们计算主成分矩阵值: P = k l ∗ α P=kl\ast\alpha P=kl∗α ,即为降维后的数据。
三:实验结果
Kpca的实现是比较成熟而且步骤不是很复杂,我们不再自己编写,主要是调用相关模块来进行实验。
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
from sklearn.decomposition import PCA
from sklearn.decomposition import KernelPCA
from sklearn.manifold import TSNE
def circle():
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
a1 = 1
r1 = 2.5
x1 = np.arange(-a1 + 0.5, a1 + 0.5, 0.05)
y1 = np.arange(-a1, a1, 0.05)
hah = 10
np.random.seed(hah)
z1 = np.sqrt(r1 ** 2 - x1 ** 2 - y1 ** 2) + np.random.uniform(0,1,len(x1))
Z1 = list(z1) + list(-z1)
Y1 = list(y1) + list(y1)
X1 = list(x1) + list(x1)
ax.scatter(X1, Y1, Z1)
a2 = 1
r2 = 1.75
x2 = np.arange(-a2, a2, 0.05)
y2 = np.arange(-a2, a2, 0.05)
np.random.seed(hah)
z2 = np.sqrt(r2 ** 2 - x2 ** 2 - y2 ** 2) + np.random.uniform(0,1,len(x1))
Z2 = list(z2) + list(-z2)
Y2 = list(y2) + list(y2)
X2 = list(x2) + list(x2)
ax.scatter(X2, Y2, Z2)
ax.set_xlabel('X Label')
ax.set_ylabel('Y Label')
ax.set_zlabel('Z Label')
plt.show()
X = X1 + X2
Y = Y1 + Y2
Z = Z1 + Z2
dn = np.array([X, Y, Z]).T
pca = PCA(n_components=2)
x_pca = pca.fit_transform(dn)
print('pca信息值:', pca.explained_variance_ratio_)
plt.figure()
plt.scatter(x_pca[:, 0][:int(len(X1))], x_pca[:, 1][:int(len(X1))], color='red', marker='^', alpha=0.5)
plt.scatter(x_pca[:, 0][int(len(X2)):], x_pca[:, 1][int(len(X2)):], color='blue', marker='o', alpha=0.5)
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.show()
kpca = KernelPCA(n_components=2, kernel='rbf', gamma=20, degree=5) ###kernel : {'linear', 'poly', 'rbf', 'sigmoid', 'cosine', 'precomputed'}, default='linear'
x_kpca = kpca.fit_transform(dn)
explained_variance = np.var(x_kpca, axis=0)
explained_variance_ratio = explained_variance / np.sum(explained_variance)
print('kpca信息值:', explained_variance_ratio)
plt.figure()
plt.scatter(x_kpca[:, 0][:int(len(X1))], x_kpca[:, 1][:int(len(X1))], color='red', marker='^', alpha=0.5)
plt.scatter(x_kpca[:, 0][int(len(X2)):], x_kpca[:, 1][int(len(X2)):], color='blue', marker='o', alpha=0.5)
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.show()
tsne = TSNE(n_components=2,metric='euclidean')
x_tsne = tsne.fit_transform(dn)
explained_variance = np.var(x_tsne, axis=0)
explained_variance_ratio = explained_variance / np.sum(explained_variance)
print('tsne信息值:', explained_variance_ratio)
plt.figure()
plt.scatter(x_tsne[:, 0][:int(len(X1))], x_tsne[:, 1][:int(len(X1))], color='red', marker='^', alpha=0.5)
plt.scatter(x_tsne[:, 0][int(len(X2)):], x_tsne[:, 1][int(len(X2)):], color='blue', marker='o', alpha=0.5)
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.show()
circle()
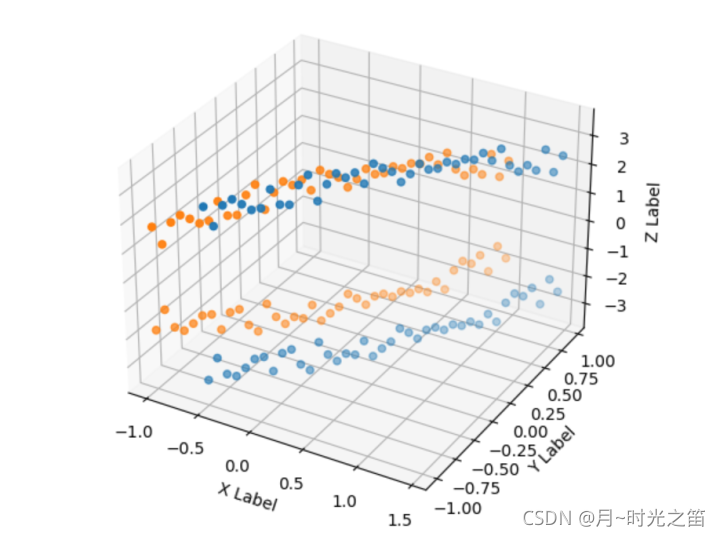

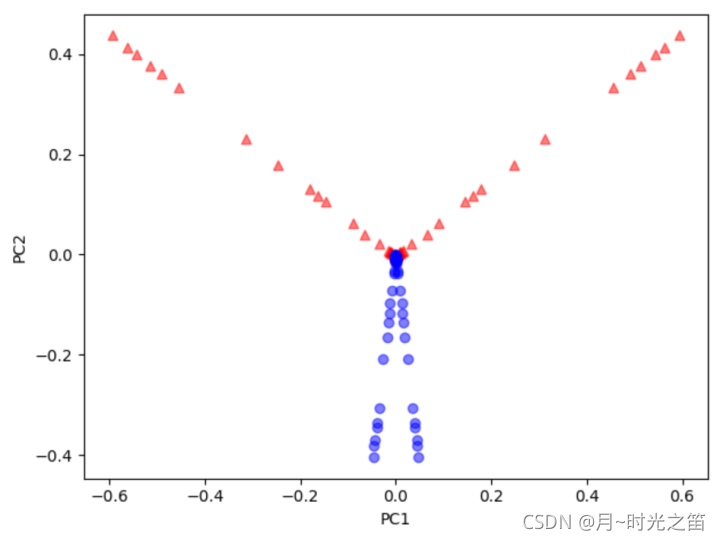
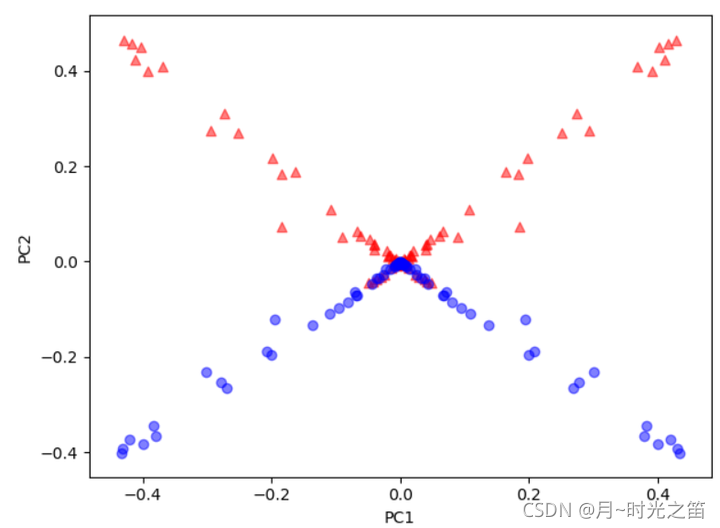
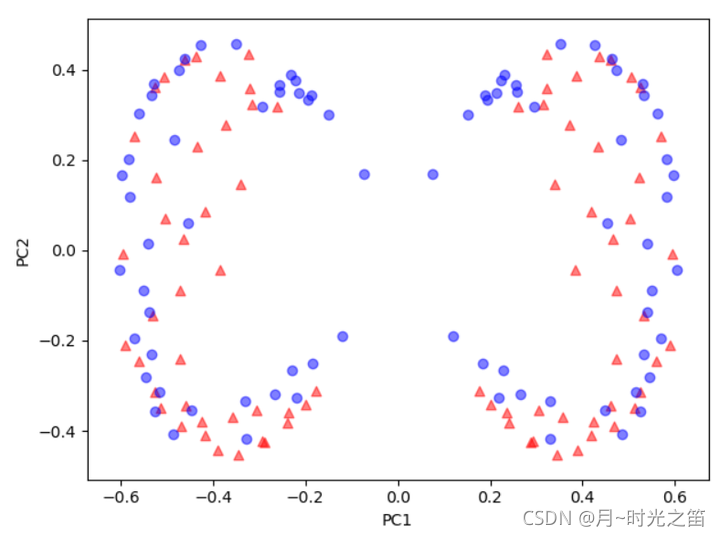
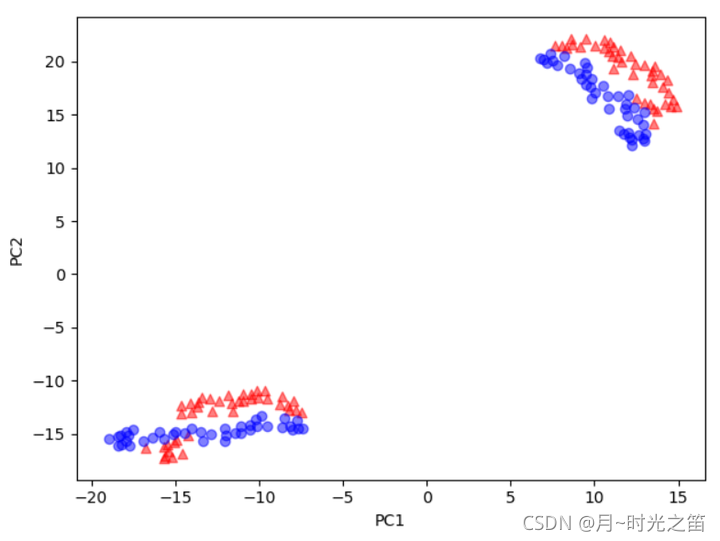
从上图3、图4我们可以看出,基于Kpca算法的降维,当核函数取高斯核时,随着gamma的增大,这时候的Kpca算法的特色就显示的淋淋尽致。降维至低维的数据很明显是线性可分的。TSNE得出的结果让低维数据分布的更加集中,但明显线性是不可分的。一般Pca降维非线性数据的效果似乎只是对高维数据做了下在低维空间的投影。
四:总结
这篇文章主要讲述了3种降维技术对非线性数据的降维处理,我们可以感受到Kpca算法在选择恰当的核函数时,会表现出明显的算法特色。普通的Pca技术在处理非线性问题方面,是很难做出相应的优化选择,所以在实际工业中,Kpca算法对于非线性数据的处理,无论是理论上的解释还是实际效果,不失为一种可靠的选择。
