KPCA,中文名称”核主成分分析“,是对PCA算法的非线性扩展。PCA是线性的,其对于非线性数据往往显得无能为力(虽然这二者的主要目的是降维,而不是分类,但也可以用于分类),其中很大一部分原因是,KPCA能够挖掘到数据集中蕴含的非线性信息。
一、KPCA较PCA存在的创新点:
1. 为了更好地处理非线性数据,引入非线性映射函数,将原空间中的数据映射到高维空间,注意,这个是隐性的,我们不知道,也不需要知道它的具体形式是啥。
2. 引入了一个定理:空间中的任一向量(哪怕是基向量),都可以由该空间中的所有样本线性表示,这点对KPCA很重要,我想大概当时那个大牛想出KPCA的时候,这点就是它最大的灵感吧。话说这和”稀疏“的思想比较像。
二、核函数定义
核函数K(kernel function)可以直接得到低维数据映射到高维后的内积,而忽略映射函数具体是什么,即K(x, y) = <φ(x), φ(y)>,其中x和y是低维的输入向量,φ是从低维到高维的映射,<x, y>是x和y的内积。核函数是一个非常有趣和强大的工具。 它是强大的,因为它提供了一个从线性到非线性的连接以及任何可以只表示两个向量之间的点积的算法。如果我们首先将我们的输入数据映射到更高维的空间,那么我在这个高维的空间进行操作出的效果,在原来那个空间就表现为非线性。
常见核函数:
(1)线性核函数:![]()
(2)多项式核函数:![]()
(3)高斯径向基核函数:
(4)拉普拉斯核函数: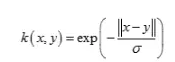
三、KPCA的简单推导:
假设原始数据是如下矩阵X:(数据每一列为一个样本,每个样本有m个属性,一共有n个样本)

将每个样本通过函数φ映射到高维空间,得到高维空间的数据矩阵φ(X)。

用同样的方法计算高维空间中数据的协方差矩阵,进一步计算特征值与特征向量。

定理:空间中的任一向量(哪怕是基向量),都可以由该空间中的所有样本线性表示,这点对KPCA很重要。
所以根据这个定理,我们就可以用所有样本来表示特征向量:

将这个线性组合带回到特征向量公式,替换特征向量,得到:

进一步,等式两边同时左乘一个 φ(X)的转置:(目的是构造2个φ(X)的转置 乘 φ(X))


等式两边同时除以K,得到:

得到了与PCA相似度极高的求解公式。
总结一下KPCA算法的计算过程
- 去除平均值,进行中心化。
- 利用核函数计算核矩阵K。
- 计算核矩阵的特征值和特征向量。
- 将特征相量按对应特征值大小从上到下按行排列成矩阵,取前k行组成矩阵P。
- P即为降维后的数据。
四、代码示例:
# -*- coding: utf-8 -*-
"""kNN和降维KernelPCA """
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets,decomposition
def load_data():
'''加载用于降维的数据。return: 一个元组,依次为训练样本集和样本集的标记'''
iris=datasets.load_iris()# 使用 scikit-learn 自带的 iris 数据集
return iris.data,iris.target
def test_KPCA(*data):
'''测试 KernelPCA 的用法
:param data: 可变参数。它是一个元组,这里要求其元素依次为:训练样本集、训练样本的标记
:return: None'''
X,y=data
kernels=['linear','poly','rbf','sigmoid']
for kernel in kernels:
kpca=decomposition.KernelPCA(n_components=None,kernel=kernel) # 依次测试四种核函数
kpca.fit(X)
print('kernel=%s --> lambdas: %s'% (kernel,kpca.lambdas_))
if __name__=='__main__':
X,y=load_data() # 产生用于降维的数据集
test_KPCA(X,y) # 调用 test_KPCA



绘制降维后样本的分布图的函数:
def plot_KPCA(*data):
''' 绘制经过 KernelPCA 降维到二维之后的样本点'''
X,y=data
kernels=['linear','poly','rbf','sigmoid']
fig=plt.figure()
colors=((1,0,0),(0,1,0),(0,0,1),(0.5,0.5,0),(0,0.5,0.5),(0.5,0,0.5),
(0.4,0.6,0),(0.6,0.4,0),(0,0.6,0.4),(0.5,0.3,0.2),)# 颜色集合,不同标记的样本染不同的颜色
for i,kernel in enumerate(kernels):
kpca=decomposition.KernelPCA(n_components=2,kernel=kernel)
kpca.fit(X)
X_r=kpca.transform(X)# 原始数据集转换到二维
ax=fig.add_subplot(2,2,i+1) ## 两行两列,每个单元显示一种核函数的 KernelPCA 的效果图
for label ,color in zip( np.unique(y),colors):
position=y==label
ax.scatter(X_r[position,0],X_r[position,1],label="target= %d"%label,
color=color)
ax.set_xlabel("X[0]")
ax.set_ylabel("X[1]")
ax.legend(loc="best")
ax.set_title("kernel=%s"%kernel)
plt.suptitle("KPCA")
plt.show() 可以看到,不同的核函数其降维后数据分布是不一样的。
可以看到,不同的核函数其降维后数据分布是不一样的。
def plot_KPCA_poly(*data):
''' 绘制经过 使用 poly 核的KernelPCA 降维到二维之后的样本点 '''
X,y=data
fig=plt.figure()
colors=((1,0,0),(0,1,0),(0,0,1),(0.5,0.5,0),(0,0.5,0.5),(0.5,0,0.5),
(0.4,0.6,0),(0.6,0.4,0),(0,0.6,0.4),(0.5,0.3,0.2),)# 颜色集合,不同标记的样本染不同的颜色
Params=[(3,1,1),(3,10,1),(3,1,10),(3,10,10),(10,1,1),(10,10,1),(10,1,10),(10,10,10)] # poly 核的参数组成的列表。
# 每个元素是个元组,代表一组参数(依次为:p 值, gamma 值, r 值)
# p 取值为:3,10
# gamma 取值为 :1,10
# r 取值为:1,10
# 排列组合一共 8 种组合
for i,(p,gamma,r) in enumerate(Params):
kpca=decomposition.KernelPCA(n_components=2,kernel='poly'
,gamma=gamma,degree=p,coef0=r) # poly 核,目标为2维
kpca.fit(X)
X_r=kpca.transform(X)# 原始数据集转换到二维
ax=fig.add_subplot(2,4,i+1)## 两行四列,每个单元显示核函数为 poly 的 KernelPCA 一组参数的效果图
for label ,color in zip( np.unique(y),colors):
position=y==label
ax.scatter(X_r[position,0],X_r[position,1],label="target= %d"%label,
color=color)
ax.set_xlabel("X[0]")
ax.set_xticks([]) # 隐藏 x 轴刻度
ax.set_yticks([]) # 隐藏 y 轴刻度
ax.set_ylabel("X[1]")
ax.legend(loc="best")
ax.set_title(r"$ (%s (x \cdot z+1)+%s)^{%s}$"%(gamma,r,p))
plt.suptitle("KPCA-Poly")
plt.show() 可以看到采用不同的多项式核函数,如果参数不同,降维后数据分布不同。
可以看到采用不同的多项式核函数,如果参数不同,降维后数据分布不同。
def plot_KPCA_rbf(*data):
''' 绘制经过 使用 rbf 核的KernelPCA 降维到二维之后的样本点 '''
X,y=data
fig=plt.figure()
colors=((1,0,0),(0,1,0),(0,0,1),(0.5,0.5,0),(0,0.5,0.5),(0.5,0,0.5),
(0.4,0.6,0),(0.6,0.4,0),(0,0.6,0.4),(0.5,0.3,0.2),)# 颜色集合,不同标记的样本染不同的颜色
Gammas=[0.5,1,4,10]# rbf 核的参数组成的列表。每个参数就是 gamma值
for i,gamma in enumerate(Gammas):
kpca=decomposition.KernelPCA(n_components=2,kernel='rbf',gamma=gamma)
kpca.fit(X)
X_r=kpca.transform(X)# 原始数据集转换到二维
ax=fig.add_subplot(2,2,i+1)## 两行两列,每个单元显示核函数为 rbf 的 KernelPCA 一组参数的效果图
for label ,color in zip( np.unique(y),colors):
position=y==label
ax.scatter(X_r[position,0],X_r[position,1],label="target= %d"%label,
color=color)
ax.set_xlabel("X[0]")
ax.set_xticks([]) # 隐藏 x 轴刻度
ax.set_yticks([]) # 隐藏 y 轴刻度
ax.set_ylabel("X[1]")
ax.legend(loc="best")
ax.set_title(r"$\exp(-%s||x-z||^2)$"%gamma)
plt.suptitle("KPCA-rbf")
plt.show() 采用同样的高斯核,参数不一样,降维后数据分布不一样。
采用同样的高斯核,参数不一样,降维后数据分布不一样。
def plot_KPCA_sigmoid(*data):
''' 绘制经过 使用 sigmoid 核的KernelPCA 降维到二维之后的样本点 '''
X,y=data
fig=plt.figure()
colors=((1,0,0),(0,1,0),(0,0,1),(0.5,0.5,0),(0,0.5,0.5),(0.5,0,0.5),
(0.4,0.6,0),(0.6,0.4,0),(0,0.6,0.4),(0.5,0.3,0.2),)# 颜色集合,不同标记的样本染不同的颜色
Params=[(0.01,0.1),(0.01,0.2),(0.1,0.1),(0.1,0.2),(0.2,0.1),(0.2,0.2)]# sigmoid 核的参数组成的列表。
# 每个元素就是一种参数组合(依次为 gamma,coef0)
# gamma 取值为: 0.01,0.1,0.2
# coef0 取值为: 0.1,0.2
# 排列组合一共有 6 种组合
for i,(gamma,r) in enumerate(Params):
kpca=decomposition.KernelPCA(n_components=2,kernel='sigmoid',gamma=gamma,coef0=r)
kpca.fit(X)
X_r=kpca.transform(X)# 原始数据集转换到二维
ax=fig.add_subplot(3,2,i+1)## 三行两列,每个单元显示核函数为 sigmoid 的 KernelPCA 一组参数的效果图
for label ,color in zip( np.unique(y),colors):
position=y==label
ax.scatter(X_r[position,0],X_r[position,1],label="target= %d"%label,
color=color)
ax.set_xlabel("X[0]")
ax.set_xticks([]) # 隐藏 x 轴刻度
ax.set_yticks([]) # 隐藏 y 轴刻度
ax.set_ylabel("X[1]")
ax.legend(loc="best")
ax.set_title(r"$\tanh(%s(x\cdot z)+%s)$"%(gamma,r))
plt.suptitle("KPCA-sigmoid")
plt.show()