学习视频:
鲁鹏-计算机视觉与深度学习
同系列往期笔记:
【学习笔记】计算机视觉与深度学习(1.线性分类器)
全连接神经网络
线性分类器通过一次变换就得出结果。
全连接神经网络级联多个变换来实现输入到输出的映射。
两层全连接网络: f = W 2 max ( 0 , W 1 x + b 1 ) + b 2 f=\mathbf{W}_2\max(0,\mathbf{W}_1\mathbf{x}+\mathbf{b}_1)+b_2 f=W2max(0,W1x+b1)+b2
三层全连接网络: f = W 3 max ( 0 , W 2 max ( 0 , W 1 x + b 1 ) + b 2 ) + b 3 f=\mathbf{W}_3\max(0, \mathbf{W}_2 \max(0, \mathbf{W}_1 \mathbf{x} + \mathbf{b}_1) +\mathbf{b}_2)+b_3 f=W3max(0,W2max(0,W1x+b1)+b2)+b3
可以发现有一个 max \max max这样一种非线性操作,这个操作不能去掉,因为一旦去掉后就退化成了线性分类器。
全连接神经网络中的权值 W \mathbf{W} W也可以看做模板,除了最外层的权值矩阵(如两层中的 W 2 \mathbf{W}_2 W2,三层中的 W 3 \mathbf{W}_3 W3)以外,其他的权值矩阵的类别数均可以人为指定(符合矩阵乘法即可)。因此,全连接神经网络的描述能力更强,因为调整这些权值矩阵行数等同于增加模板个数,分类器有机会学习到更多信息。
线性分类器能够解决线性可分的任务,即上一节中所述的分界面。线性可分指至少存在一个线性分界面能把两类样本没有错误的分开。
全连接神经网络更多的是处理线性不可分的任务。
线性可分示例:
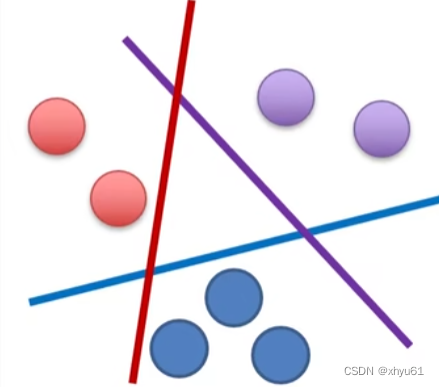
线性不可分示例:
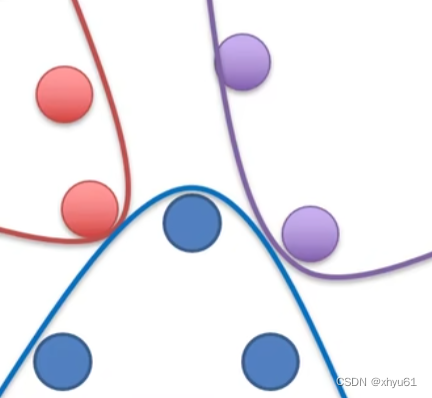
对于两层全连接网络:
f = W 2 max ( 0 , W 1 x + b 1 ) + b 2 f=\mathbf{W}_2\max(0,\mathbf{W}_1\mathbf{x}+\mathbf{b}_1)+b_2 f=W2max(0,W1x+b1)+b2
其结构如下图所示:
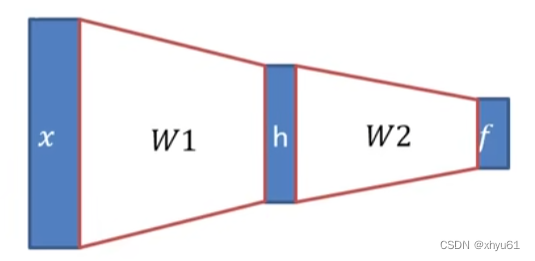
画成神经网络的样子:
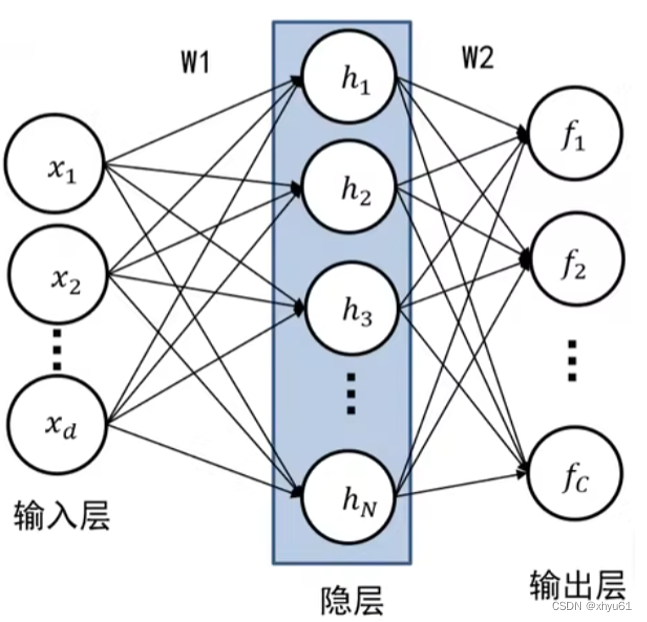
我们定义N层全连接神经网络为:除输入层以外,其它层的数量为N的网络。
三层全连接神经网络如下图所示。
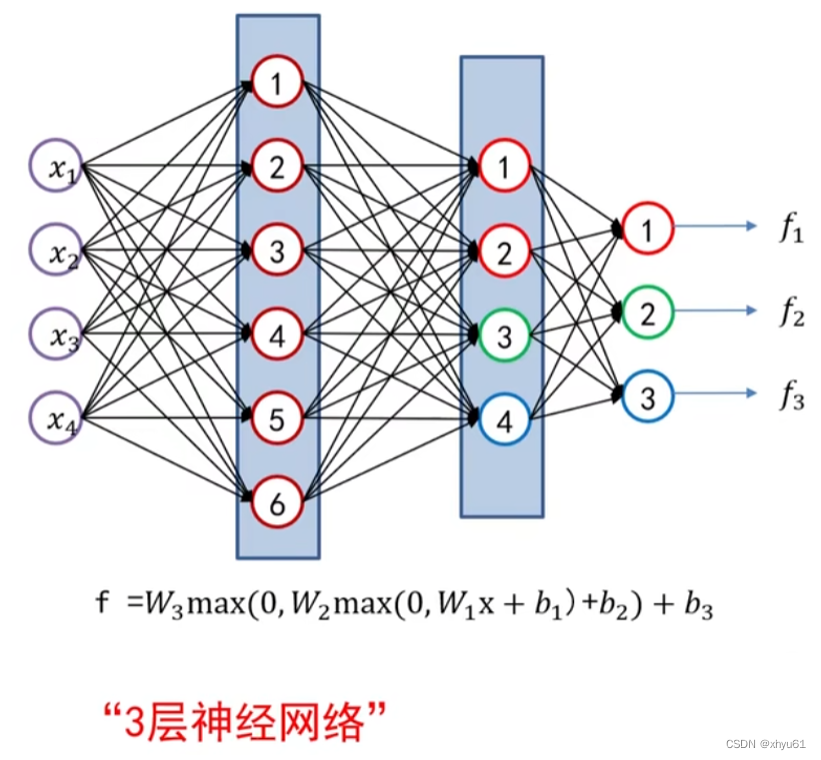
1 激活函数
问 为什么需要非线性操作?
答 若不采取如 max \max max的非线性操作,多层全连接神经网络会退化成为线性。
两层全连接网络: f = W 2 max ( 0 , W 1 x + b 1 ) + b 2 f=\mathbf{W}_2\max(0,\mathbf{W}_1\mathbf{x}+\mathbf{b}_1)+b_2 f=W2max(0,W1x+b1)+b2
三层全连接网络: f = W 3 max ( 0 , W 2 max ( 0 , W 1 x + b 1 ) + b 2 ) + b 3 f=\mathbf{W}_3\max(0, \mathbf{W}_2 \max(0, \mathbf{W}_1 \mathbf{x} + \mathbf{b}_1) +\mathbf{b}_2)+b_3 f=W3max(0,W2max(0,W1x+b1)+b2)+b3
上式中的 max \max max这样的非线性操作就是激活函数。
1.1 Sigmoid
1 1 + e − x \frac{1}{1+e^{-x}} 1+e−x1
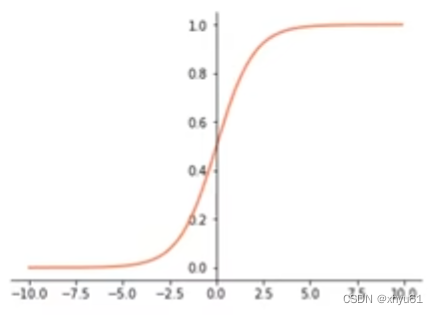
Sigmoid函数当 x → − 5.0 x\rightarrow -5.0 x→−5.0时逐渐趋近于 0 0 0,当 x → 5.0 x\rightarrow 5.0 x→5.0时逐渐趋近于 1 1 1。使用Sigmoid作为激活函数,使向量中的数值值域变成 [ 0 , 1 ] [0,1] [0,1]。其特点为:输出值均为正数,且不以原点作为中心点。
1.2 tanh
e x − e − x e x + e − x \frac{e^x-e^{-x}}{e^x+e^{-x}} ex+e−xex−e−x
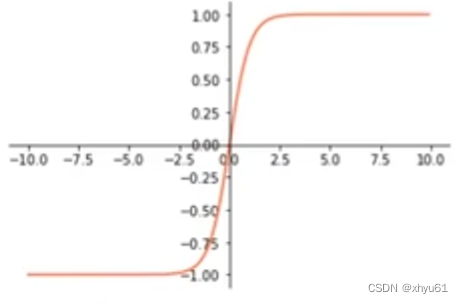
tanh函数当 x → − 2.5 x\rightarrow -2.5 x→−2.5时逐渐趋近于 − 1 -1 −1,当 x → 2 , 5 x\rightarrow 2,5 x→2,5时逐渐趋近于 1 1 1。使用tanh函数作为激活函数,使向量中的数值值域变成 [ − 1 , 1 ] [-1,1] [−1,1]。其特点为:以原点为中心点,保留原始数据的对称性质(这对很多情况下的学习都很重要)。
1.3 ReLU
max ( 0 , x ) \max(0,x) max(0,x)
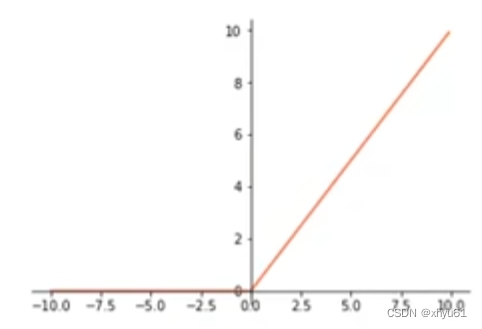
1.4 Leaky ReLU
max ( 0.1 x , x ) \max(0.1x,x) max(0.1x,x)

2 网络结构设计
- 用不用隐层,用一个隐层还是用几个隐层?(深度设计)
- 每个隐层设置多少个神经元比较合适?(宽度设计)
这两个问题都没有一个准确的答案。
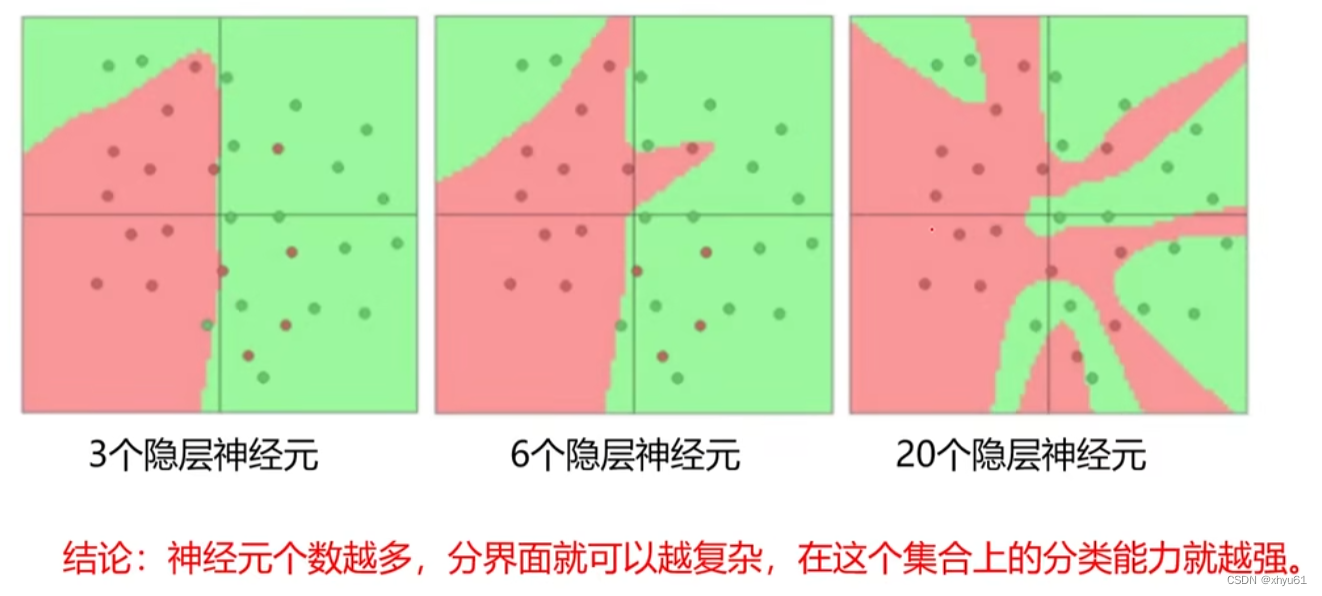
依据分类任务的难易程度来调整神经网络模型的复杂程度,分类任务越难,我们设计的神经网络结构就应该越深、越宽。但是,需要注意的是对训练集分类精度最高的全连接神经网络模型,在真实场景下识别的性能未必是最好的(过拟合)。
3 SOFTMAX
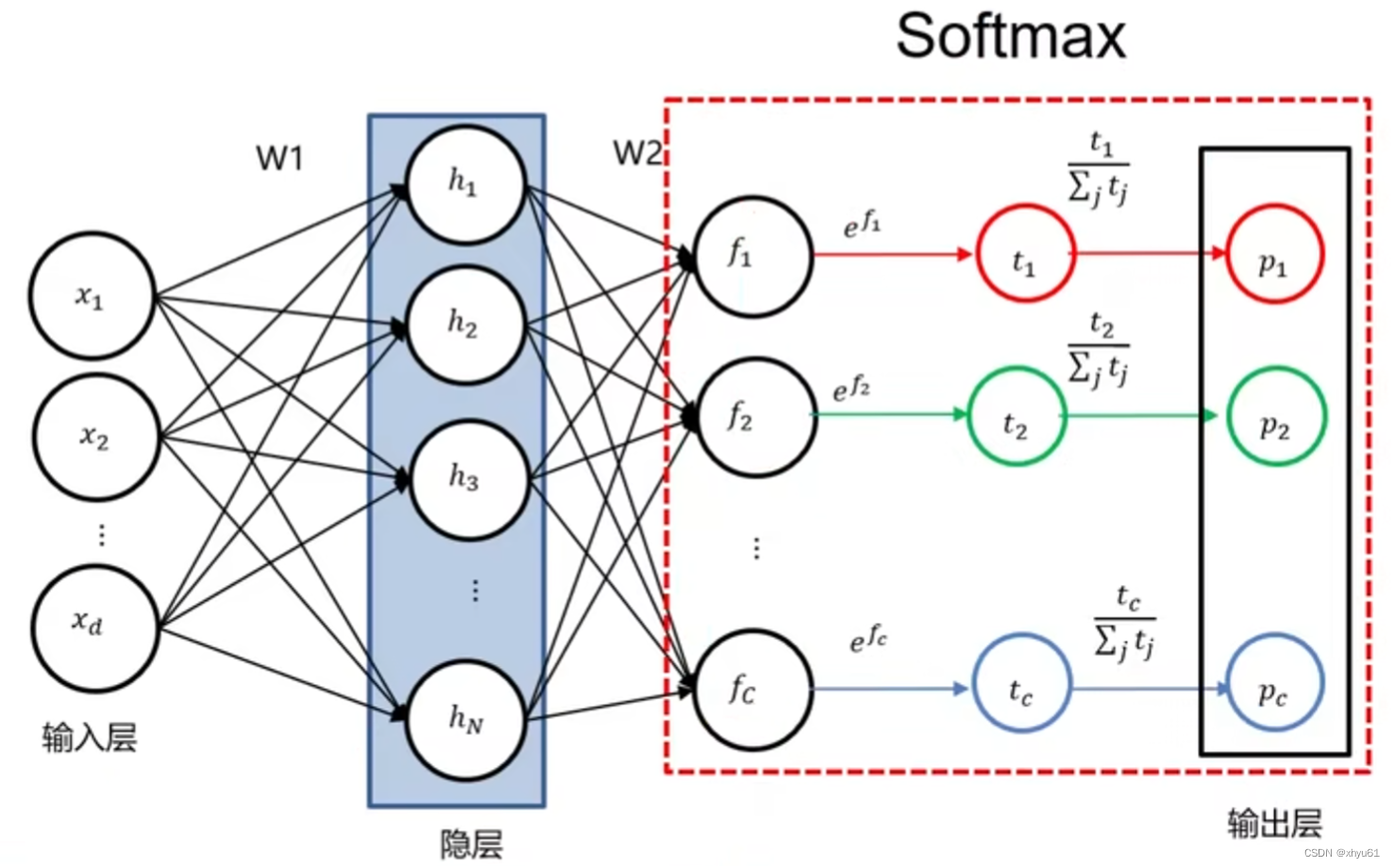
之所以采用 e f i e^{f_i} efi,是为了防止后续分母出现 0 0 0。

4 交叉熵损失
4.1 One-Hot
One-Hot编码,又称为一位有效编码,主要是采用N位状态寄存器来对N个状态进行编码,每个状态都由他独立的寄存器位,并且在任意时候只有一位有效。
One-Hot编码是分类变量作为二进制向量的表示。这首先要求将分类值映射到整数值。然后,每个整数值被表示为二进制向量,除了整数的索引之外,它都是零值,它被标记为1。
对于图像识别问题,以上面的示例为例子,对于那张图像的真实值应表示为 [ 1 , 0 , 0 ] [1,0,0] [1,0,0],要么是,要么不是,只有 0 0 0和 1 1 1两种选择。
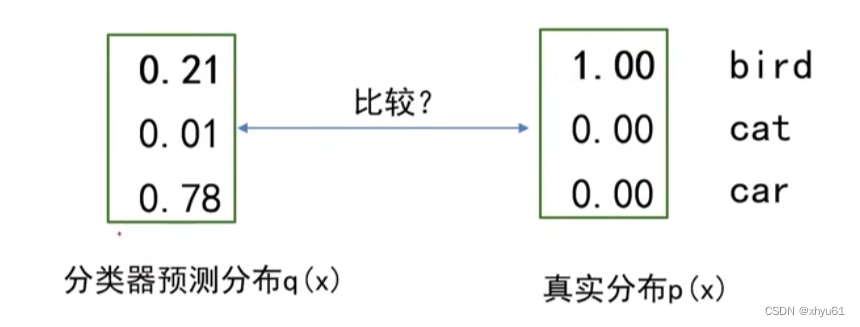
如何度量现在的分类器输出与预测值之间的距离?
4.2 熵
H ( p ) = − ∑ x p ( x ) log p ( x ) H(p)=-\displaystyle\sum\limits_{x} p(x)\log p(x) H(p)=−x∑p(x)logp(x)
结论:
有 c c c个类别时,对于所有 ∀ i ∈ [ 1 , c ] \forall i∈[1,c] ∀i∈[1,c]有 p ( x i ) = 1 c p(x_i)=\frac{1}{c} p(xi)=c1,此时熵为最大。
有 c c c个类别时,对于所有 ∀ i ∈ [ 1 , c ] \forall i∈[1,c] ∀i∈[1,c]有且仅有一个 i i i满足 x i = 1 x_i=1 xi=1,其余均为 0 0 0,此时熵为最小,熵值为 0 0 0。
4.3 相对熵(KL散度)
K L ( p ∣ ∣ q ) = − ∑ x p ( x ) log q ( x ) p ( x ) KL(p||q)=-\displaystyle\sum\limits_{x} p(x)\log \frac{q(x)}{p(x)} KL(p∣∣q)=−x∑p(x)logp(x)q(x)
相对熵也称KL散度,用来度量两个分布之间的不相似性。和距离的概念不同,通常 K L ( p ∣ ∣ q ) ≠ K L ( q ∣ ∣ p ) KL(p||q)\neq KL(q||p) KL(p∣∣q)=KL(q∣∣p)。
4.4 交叉熵
H ( p , q ) = − ∑ x p ( x ) log q ( x ) H(p,q)=-\displaystyle\sum\limits_{x} p(x)\log q(x) H(p,q)=−x∑p(x)logq(x)
p ( x ) p(x) p(x)和 q ( x ) q(x) q(x)为两种不同的分布。
不难发现:
H ( p , q ) = − ∑ x p ( x ) log q ( x ) = − ∑ x p ( x ) log q ( x ) − ∑ x p ( x ) log p ( x ) + ∑ x p ( x ) log p ( x ) = − ∑ x p ( x ) log p ( x ) − ∑ x p ( x ) log q ( x ) p ( x ) = H ( p ) + K L ( p ∣ ∣ q ) \begin{aligned} H(p,q) &= -\displaystyle\sum\limits_{x} p(x) \log q(x) \\ &=-\displaystyle\sum\limits_{x} p(x) \log q(x) - \displaystyle\sum\limits_{x} p(x) \log p(x) + \displaystyle\sum\limits_{x} p(x) \log p(x) \\ &=- \displaystyle\sum\limits_{x} p(x) \log p(x) - \displaystyle\sum\limits_{x} p(x)\log \frac{q(x)}{p(x)} \\ &=H(p)+KL(p||q) \end{aligned} H(p,q)=−x∑p(x)logq(x)=−x∑p(x)logq(x)−x∑p(x)logp(x)+x∑p(x)logp(x)=−x∑p(x)logp(x)−x∑p(x)logp(x)q(x)=H(p)+KL(p∣∣q)
当处于One-Hot情况下时, H ( p ) = 0 H(p)=0 H(p)=0。此时有 H ( p , q ) = K L ( p ∣ ∣ q ) H(p,q)=KL(p||q) H(p,q)=KL(p∣∣q)。因此一般通过交叉熵定义两种分类器的差距。

而计算交叉熵时不难发现,在One-Hot模型下,只有 p ( x j ) = 1 p(x_j)=1 p(xj)=1对应的 j j j类别对交叉熵是有贡献的。此时 L i = − log ( q j ) L_i=-\log(q_j) Li=−log(qj)。
不是One-Hot时,不能使用 H ( p , q ) = K ( p ∣ ∣ q ) H(p,q)=K(p||q) H(p,q)=K(p∣∣q)的结论,此时需要使用相对熵计算。
4.5 交叉熵损失vs多类支撑向量机损失
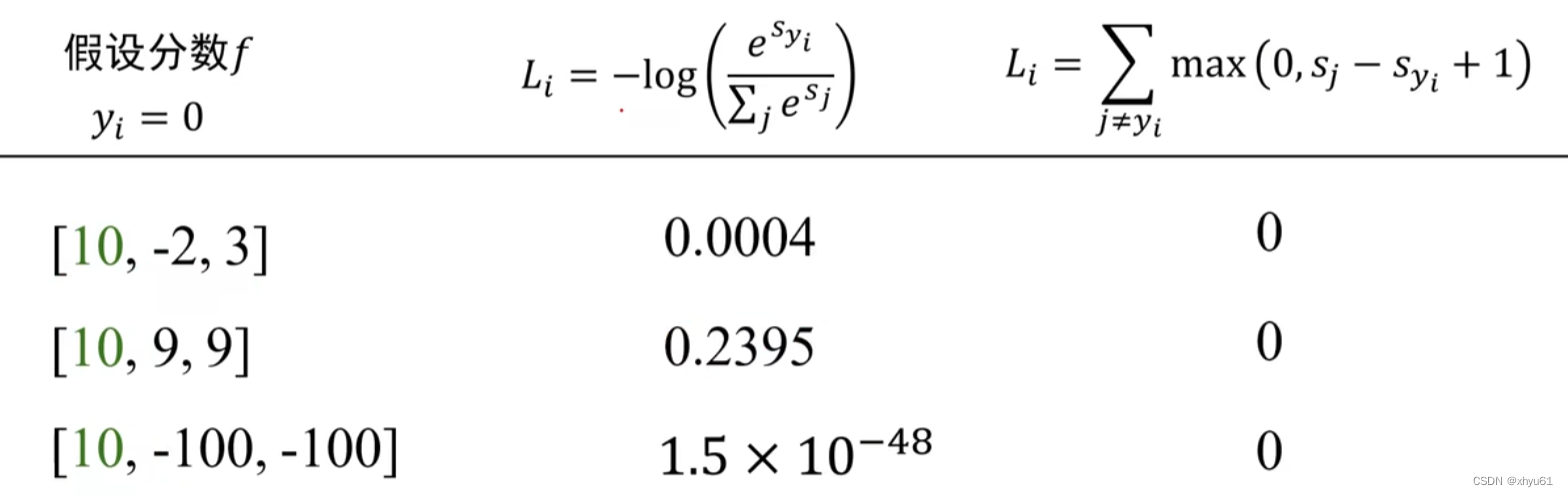
不难看出,多类支撑向量机损失在预测正确的情况下分不出分类器的好坏,但是交叉熵可以体现出其可靠性差别。
5 计算图
5.1 计算图构建与计算
计算图是一种有向图,它用来表达输入、输出以及中间变量之间的计算关系,图中的每个节点对应着一种数学运算。
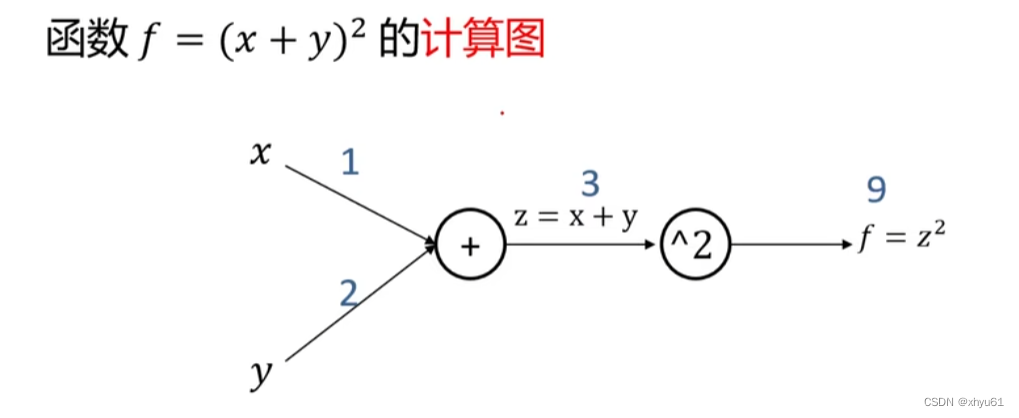

- 任何复杂的函数,都可以用计算图的形式表示;
- 在整个计算图中,每个门单元都会得到一些输入,然后进行下列值的计算:①这个门的计算②其输出值关于输入值的局部梯度。
- 利用链式法则,门单元应该将回传的梯度乘以它对其的输入的局部梯度,从而得到整个网络的输出对该门单元的每个输入值的梯度。
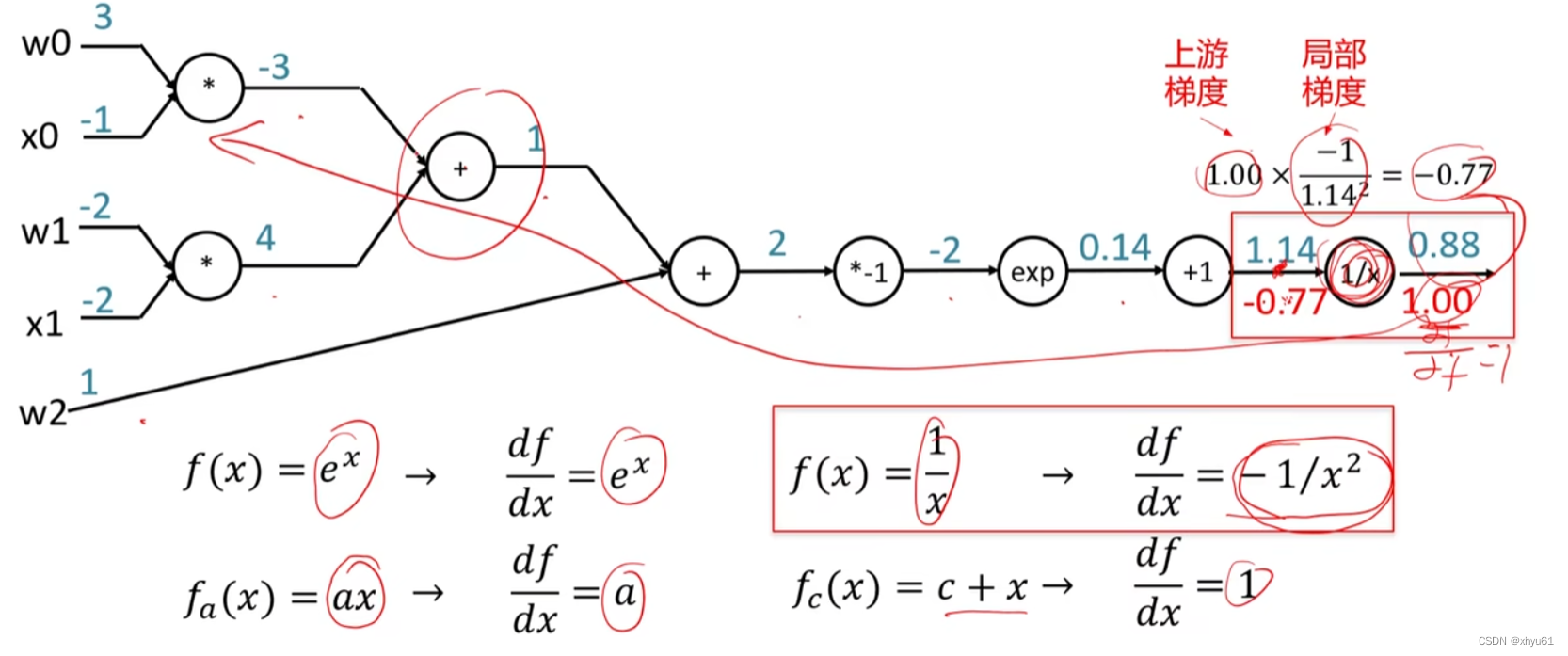
上图为 f ( w , x ) = 1 1 + e − ( w 0 x 0 + w 1 x 1 + w 2 ) f(w,x)=\frac{1}{1+e^{-(w_0x_0+w_1x_1+w_2)}} f(w,x)=1+e−(w0x0+w1x1+w2)1的计算图。给出 w 0 , x 0 , w 1 , x 1 , w 2 w_0,x_0,w_1,x_1,w_2 w0,x0,w1,x1,w2的值,从左到右正向可以推出最终的结果。而从右往左,可以求出梯度,最后通过链式求导法的原理得到整体的梯度。
5.2 计算图的颗粒度
σ ( x ) = 1 1 + e − x \sigma(x)=\frac{1}{1+e^{-x}} σ(x)=1+e−x1
d σ ( x ) d x = ( 1 − σ ( x ) ) ( σ ( x ) ) \frac{d\sigma (x)}{dx}=(1-\sigma(x))(\sigma(x)) dxdσ(x)=(1−σ(x))(σ(x))
可以看出,如果我们在计算图中不把sigmoid函数部分拆解开来,而是当做一个运算进行构建,那么会得到:
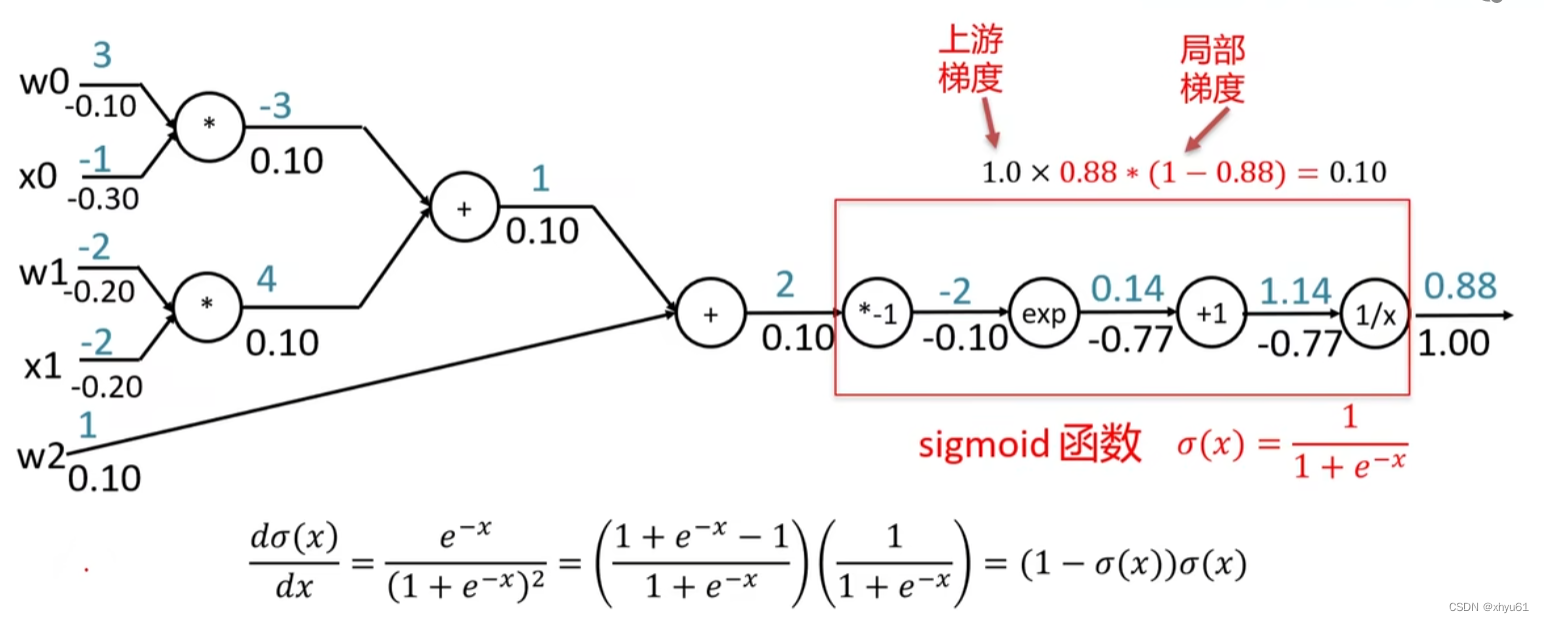
这样就简化了图的单元个数,换句话说就是降低了计算图的颗粒度。
降低颗粒度可以提高计算效率,但是对于计算图中的一个单元而言,实现难度提升。
5.3 计算图中的门单元
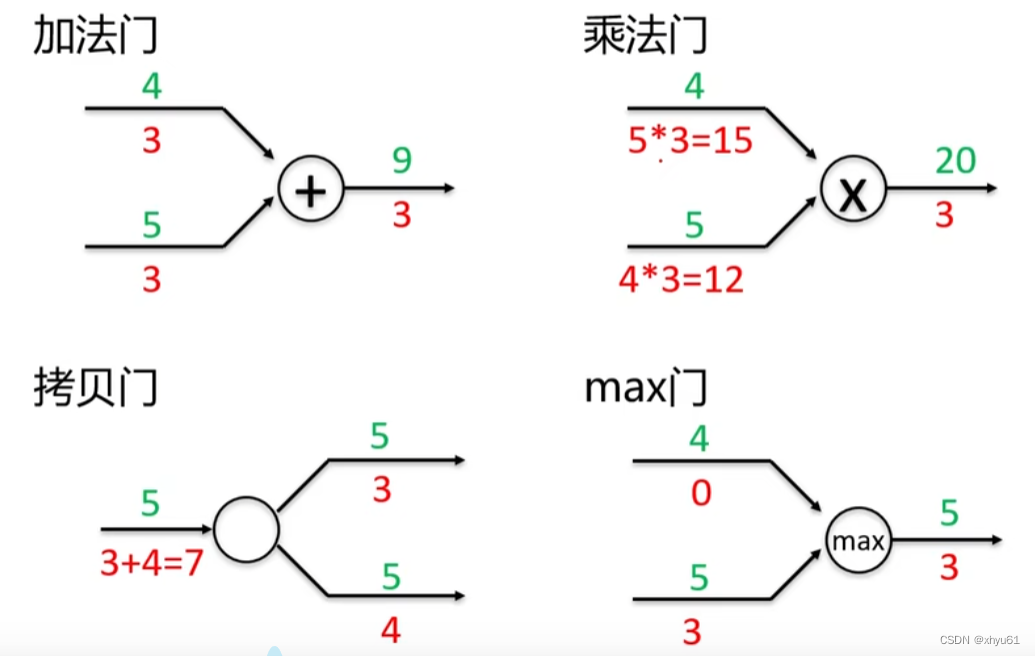
5.4 链式法则导致的梯度问题
梯度消失
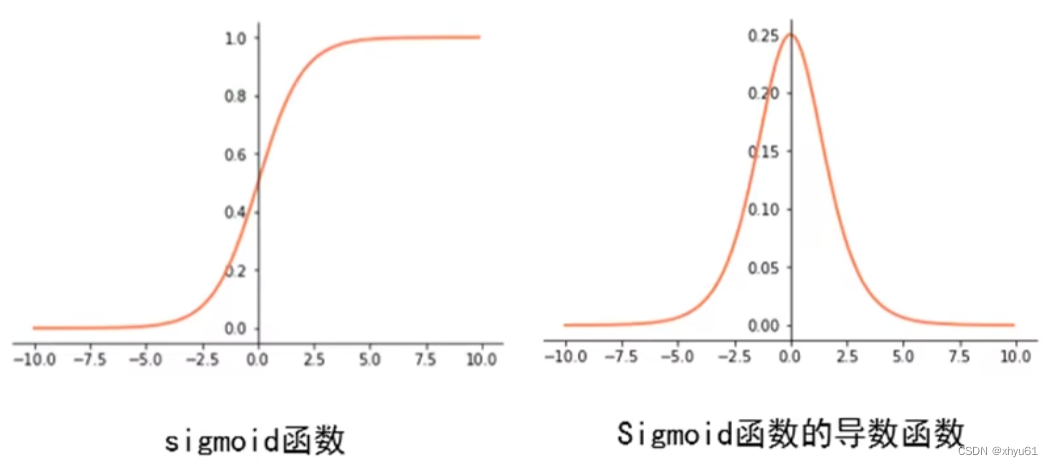
从导数图像不难看出,当输入值大于10或小于-10时,局部梯度都是0,这非常不利于网络的梯度流传递。tanh函数也是同理。
梯度消失是神经网络训练中非常致命的一个问题,其本质是由于链式法则的乘法特性导致的。
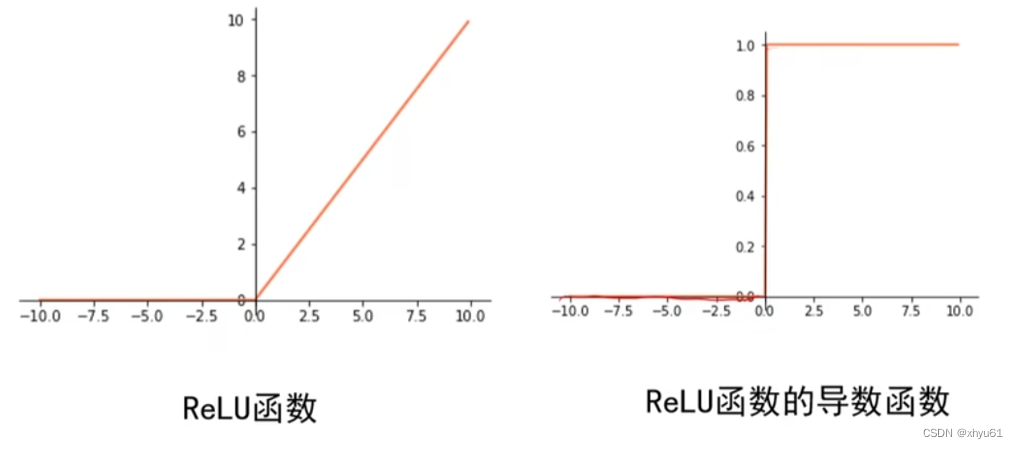
当输入大于0时,使用ReLU函数,局部梯度永远不会为0,比较有利于梯度流的传递。
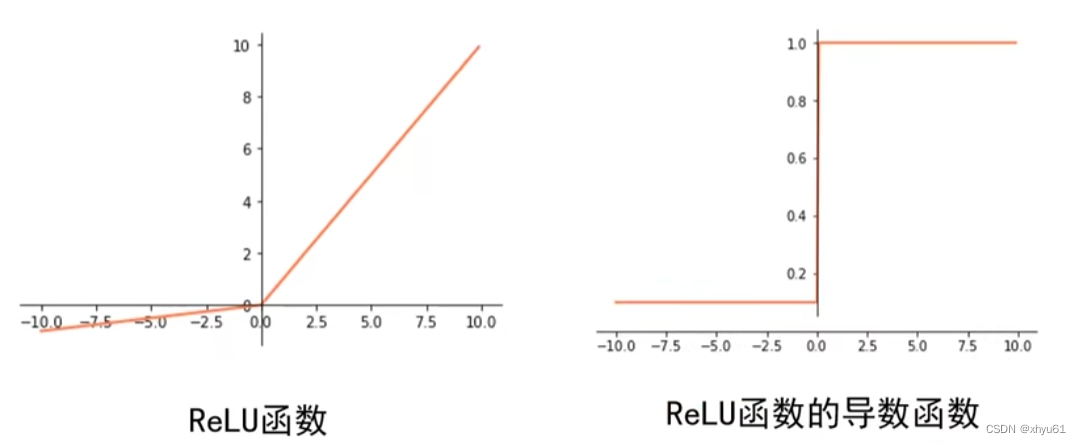
Leakly ReLU函数基本不会出现梯度为0的情况,之所以说基本,是因为函数在 x = 0 x=0 x=0处不存在导数。
结论 尽量选择ReLU函数或Leakly ReLU函数,相对于Sigmoid/tanh,ReLU函数或者Leakly ReLU函数会让梯度流更加顺畅,训练过程收敛得更快。
梯度爆炸
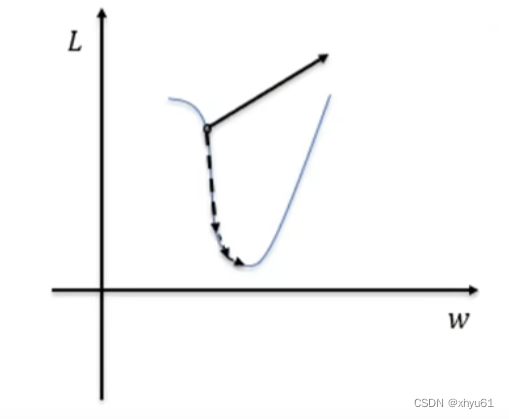
梯度爆炸也是由于链式法则的乘法特性导致的。断崖处梯度乘以学习率后会是一个非常大的数值,从而“飞”出了合理区域,最终导致算法不收敛。
解决方案:把沿梯度方向前进的步长限制在某个值内就可以避免“飞”出了,这个方法也称为梯度裁剪。
相比之下,梯度爆炸的问题更明显一些,因为它不像梯度爆炸,具有解决办法。
6 梯度算法改进
6.1 梯度下降法存在的问题
回顾小批量梯度下降算法:
Require:学习率 ϵ \epsilon ϵ、初始参数 θ \theta θ
while 停止标准为满足 do:
1.从训练集中采样 m m m(批量大小)个样本 { x ( 1 ) , ⋯ , x ( m ) } \{x^{(1)},\cdots,x^{(m)}\} { x(1),⋯,x(m)}和对应的目标 { y ( 1 ) , ⋯ , y ( m ) } \{y^{(1)},\cdots,y^{(m)}\} { y(1),⋯,y(m)}
2.计算梯度: g ← 1 m ∇ θ ∑ i L ( f ( x ( i ) ; θ ) , y ( i ) ) g\leftarrow\frac{1}{m}\nabla_\theta\displaystyle\sum\limits_{i} L(f(\mathbf{x}^{(i)};\theta),\mathbf{y}^{(i)}) g←m1∇θi∑L(f(x(i);θ),y(i))
3.更新权值: θ ← θ − ϵ g \theta \leftarrow \theta - \epsilon g θ←θ−ϵg
end while
损失函数特性:一个方向上变化迅速而在另一个方向上变化缓慢。
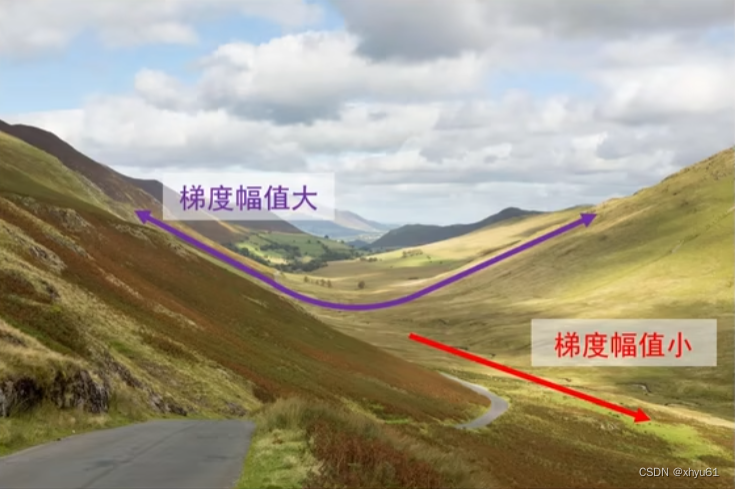
我们的优化目标:从起点处走到底部笑脸处。

梯度下降算法存在的问题:山壁间震荡,往低谷方向的行进较慢。
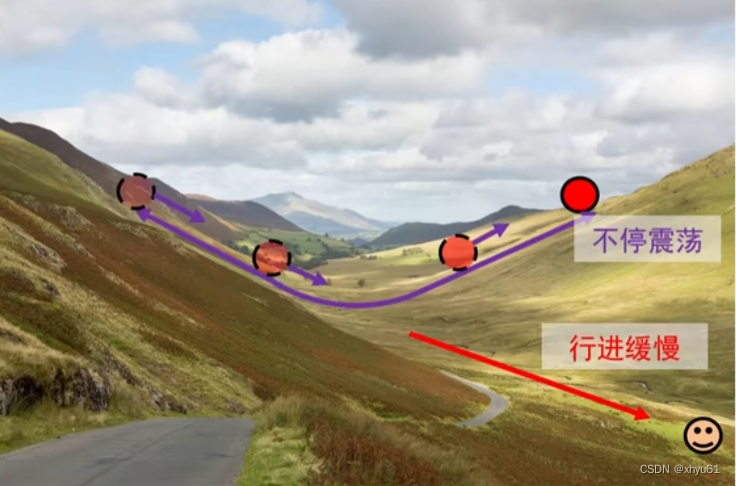
仅增大步长并不能加快算法收敛速度!
6.2 动量法
目标:改进梯度下降算法存在的问题,即减少震荡,加速通往谷底。
改进思想:利用累加历史梯度值信息更新梯度。
Require:学习率 ϵ \epsilon ϵ、动量系数 μ \mu μ、初始参数 θ \theta θ
初始化速度 v = 0 v=0 v=0
while 停止标准为满足 do:
1.从训练集中采样 m m m(批量大小)个样本 { x ( 1 ) , ⋯ , x ( m ) } \{x^{(1)},\cdots,x^{(m)}\} { x(1),⋯,x(m)}和对应的目标 { y ( 1 ) , ⋯ , y ( m ) } \{y^{(1)},\cdots,y^{(m)}\} { y(1),⋯,y(m)}
2.计算梯度: g ← 1 m ∇ θ ∑ i L ( f ( x ( i ) ; θ ) , y ( i ) ) g\leftarrow\frac{1}{m}\nabla_\theta\displaystyle\sum\limits_{i} L(f(\mathbf{x}^{(i)};\theta),\mathbf{y}^{(i)}) g←m1∇θi∑L(f(x(i);θ),y(i))
3.速度更新: v = μ v + g v=\mu v+g v=μv+g
4.更新权值: θ ← θ − ϵ v \theta \leftarrow \theta - \epsilon v θ←θ−ϵv
end while
其中 μ \mu μ的取值范围 [ 0 , 1 ) [0,1) [0,1), μ = 0 \mu=0 μ=0时等价于梯度下降算法,建议设置 0.9 0.9 0.9。
为什么有效?
累加过程中震荡方向互相抵消,平坦的方向就得到了增强。
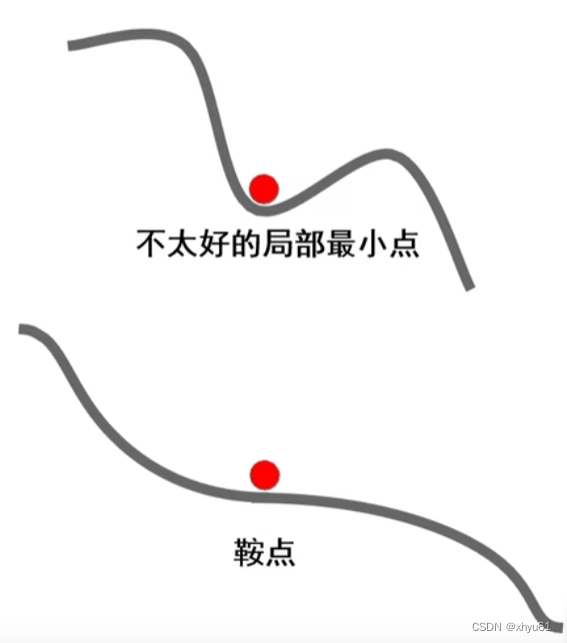
现象:损失函数常具有不太好的局部最小点或者鞍点(高维空间常见)
梯度下降算法存在的问题 局部最小处与鞍点处梯度为0,算法无法通过。
动量法的优势 由于动量的存在,算法可以冲出局部最小点以及鞍点,找到更优的解。
6.3 自适应梯度法
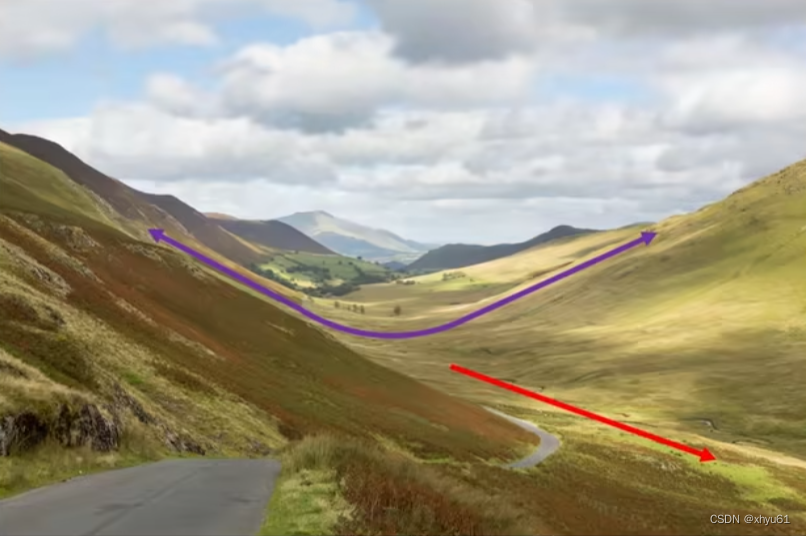
自适应梯度法通过减小震荡方向步长,增大平坦方向步长来减小震荡,加速通往谷底方向。
问 如何区分震荡方向与平坦方向?
答 梯度幅度的平方较大的方向是震荡方向;梯度幅度的平方较小的方向是平坦方向。
AdaGrad方法是一种自适应梯度算法。
Require:学习率 ϵ \epsilon ϵ、衰减速率 ρ \rho ρ、初始参数 θ \theta θ、小常数 δ \delta δ(用于被小数除时的数值稳定,通常设置为 1 0 − 5 10^{-5} 10−5)
初始化累计变量 r = 0 r=0 r=0
while 停止标准为满足 do:
1.从训练集中采样 m m m(批量大小)个样本 { x ( 1 ) , ⋯ , x ( m ) } \{x^{(1)},\cdots,x^{(m)}\} { x(1),⋯,x(m)}和对应的目标 { y ( 1 ) , ⋯ , y ( m ) } \{y^{(1)},\cdots,y^{(m)}\} { y(1),⋯,y(m)}
2.计算梯度: g ← 1 m ∇ θ ∑ i L ( f ( x ( i ) ; θ ) , y ( i ) ) g\leftarrow\frac{1}{m}\nabla_\theta\displaystyle\sum\limits_{i} L(f(\mathbf{x}^{(i)};\theta),\mathbf{y}^{(i)}) g←m1∇θi∑L(f(x(i);θ),y(i))
3.累积平方梯度: r = r + g ∗ g r=r+g*g r=r+g∗g
4.更新权值: w ← w − ϵ r + δ g w \leftarrow w - \frac{\epsilon}{\sqrt{r}+\delta} g w←w−r+δϵg
end while
其中 ρ \rho ρ的取值范围为 [ 0 , 1 ) [0,1) [0,1), ρ = 0 \rho=0 ρ=0时仅考虑当前梯度的强度,建议设置 0.999 0.999 0.999
RMSProp方法是一种自适应梯度算法,是AdaGrad算法的一种改进。AdaGrad算法在 r r r很大时,会导致权值 w w w的调整速度非常之缓慢,而累计平方梯度只会越来越大,使学习效率大大降低。RMSProp算法使用衰减速率 ρ \rho ρ来削弱累积平方梯度,从而解决上述问题。
Require:学习率 ϵ \epsilon ϵ、衰减速率 ρ \rho ρ、初始参数 θ \theta θ、小常数 δ \delta δ(用于被小数除时的数值稳定,通常设置为 1 0 − 5 10^{-5} 10−5)
初始化累计变量 r = 0 r=0 r=0
while 停止标准为满足 do:
1.从训练集中采样 m m m(批量大小)个样本 { x ( 1 ) , ⋯ , x ( m ) } \{x^{(1)},\cdots,x^{(m)}\} { x(1),⋯,x(m)}和对应的目标 { y ( 1 ) , ⋯ , y ( m ) } \{y^{(1)},\cdots,y^{(m)}\} { y(1),⋯,y(m)}
2.计算梯度: g ← 1 m ∇ θ ∑ i L ( f ( x ( i ) ; θ ) , y ( i ) ) g\leftarrow\frac{1}{m}\nabla_\theta\displaystyle\sum\limits_{i} L(f(\mathbf{x}^{(i)};\theta),\mathbf{y}^{(i)}) g←m1∇θi∑L(f(x(i);θ),y(i))
3.累积平方梯度: r ← ρ r + ( 1 − ρ ) g ∗ g r \leftarrow \rho r+(1-\rho)g*g r←ρr+(1−ρ)g∗g
4.更新权值: w ← w − ϵ r + δ g w \leftarrow w - \frac{\epsilon}{\sqrt{r}+\delta} g w←w−r+δϵg
end while
其中 ρ \rho ρ的取值范围为 [ 0 , 1 ) [0,1) [0,1), ρ = 0 \rho=0 ρ=0时仅考虑当前梯度的强度,建议设置 0.999 0.999 0.999
6.4 Adam
Adam算法同时使用动量与自适应梯度思想。其中步骤5中修正偏差可以极大缓解算法初期的冷启动问题。
Require:学习率 ϵ \epsilon ϵ、衰减速率 ρ \rho ρ、动量系数 μ \mu μ、初始参数 θ \theta θ、小常数 δ \delta δ(用于被小数除时的数值稳定,通常设置为 1 0 − 5 10^{-5} 10−5)
初始化累计变量 r = 0 , v = 0 r=0,v=0 r=0,v=0
while 停止标准为满足 do:
1.从训练集中采样 m m m(批量大小)个样本 { x ( 1 ) , ⋯ , x ( m ) } \{x^{(1)},\cdots,x^{(m)}\} { x(1),⋯,x(m)}和对应的目标 { y ( 1 ) , ⋯ , y ( m ) } \{y^{(1)},\cdots,y^{(m)}\} { y(1),⋯,y(m)}
2.计算梯度: g ← 1 m ∇ θ ∑ i L ( f ( x ( i ) ; θ ) , y ( i ) ) g\leftarrow\frac{1}{m}\nabla_\theta\displaystyle\sum\limits_{i} L(f(\mathbf{x}^{(i)};\theta),\mathbf{y}^{(i)}) g←m1∇θi∑L(f(x(i);θ),y(i))
3.累积梯度: v ← μ v + ( 1 − μ ) g v \leftarrow \mu v +(1-\mu)g v←μv+(1−μ)g
4.累积平方梯度: r ← ρ r + ( 1 − ρ ) g ∗ g r \leftarrow \rho r+(1-\rho)g*g r←ρr+(1−ρ)g∗g
5,修正偏差: v ~ = v 1 − μ t \tilde{v}=\frac{v}{1-\mu^t} v~=1−μtv; r ~ = r 1 − ρ t \tilde{r}=\frac{r}{1-\rho^t} r~=1−ρtr( t t t为迭代轮次)
4.更新权值: w ← w − ϵ r ~ + δ g w \leftarrow w - \frac{\epsilon}{\sqrt{\tilde{r}}+\delta} g w←w−r~+δϵg
end while
其中 ρ \rho ρ的取值范围为 [ 0 , 1 ) [0,1) [0,1), ρ = 0 \rho=0 ρ=0时仅考虑当前梯度的强度,建议设置 0.999 0.999 0.999; μ \mu μ的取值范围 [ 0 , 1 ) [0,1) [0,1), μ = 0 \mu=0 μ=0时等价于梯度下降算法,建议设置 0.9 0.9 0.9。
7 权值初始化
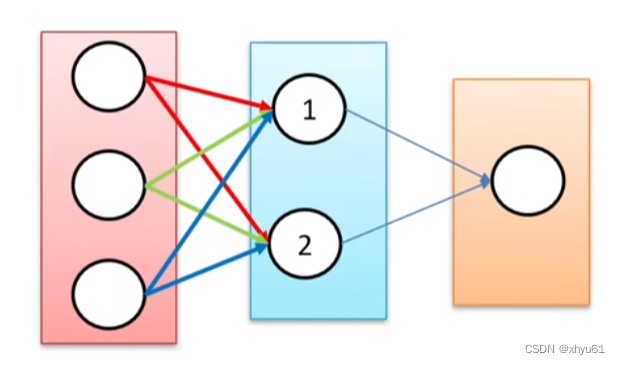
所谓权值矩阵中的权值,其实就是上图中每一条边的权值。这一节我们讨论如何在学习开始时对这些权值进行初始化。
7.1 全零初始化导致的问题
全零初始化:网络中不同的神经元有相同的输出,进行同样的更新,因此,这些神经元学到的参数都一样,等价于一个神经元。
建议采用随机初始化,避免全零初始化!
7.2 随机权值初始化中的梯度消失
网络结构:10个隐层,1个输出层,每个隐层含有500个神经元,使用的是tanh激活函数。
随机初始化方式:权值采样自 N ( 0 , 0.01 ) N(0,0.01) N(0,0.01)的高斯分布。

最后的输出都变为0了(梯度消失)
随机初始化方式2:权值采样自 N ( 0 , 1 ) N(0,1) N(0,1)的高斯分布。

最后的输出都变为-1或1了。
原因:Sigmoid函数和tanh函数都具有这样梯度消失的情况。从生物学上来说,是因为人脑的细胞接受刺激从而产生活动,首先需要一定的阈值,没有达到阈值,几乎没用。而不同的刺激产生的输 出也是不同的,达到一定值后就饱和了,再加大也没用。
Sigmoid函数
σ ( x ) = 1 1 + e − z \sigma(x)=\frac{1}{1+e^{-z}} σ(x)=1+e−z1
d σ ( x ) d x = σ ( x ) ( 1 − σ ( x ) ) \frac{d\sigma(x)}{dx}=\sigma(x)(1-\sigma(x)) dxdσ(x)=σ(x)(1−σ(x))
根据Sigmoid函数图像可得, x x x很小时 σ ( x ) → 0 \sigma(x)\rightarrow 0 σ(x)→0, x x x很大时 σ ( x ) → 1 \sigma(x)\rightarrow 1 σ(x)→1。观察导函数,当 x x x很小或很大时均有 d σ ( x ) d x → 0 \frac{d\sigma(x)}{dx} \rightarrow 0 dxdσ(x)→0。这会造成梯度消失的现象。
tanh函数
f ( x ) = t a n h ( x ) = e x − e − x e x + e − x f(x)=tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}} f(x)=tanh(x)=ex+e−xex−e−x
d f ( x ) d x = 1 − ( f ( x ) ) 2 \frac{df(x)}{dx}=1-(f(x))^2 dxdf(x)=1−(f(x))2
根据Sigmoid函数图像可得, x x x很小时 σ ( x ) → − 1 \sigma(x)\rightarrow -1 σ(x)→−1, x x x很大时 σ ( x ) → 1 \sigma(x)\rightarrow 1 σ(x)→1。观察导函数,当 x x x很小或很大时均有 d f ( x ) d x → 0 \frac{df(x)}{dx} \rightarrow 0 dxdf(x)→0。这会造成梯度消失的现象。
7.3 Xavier初始化
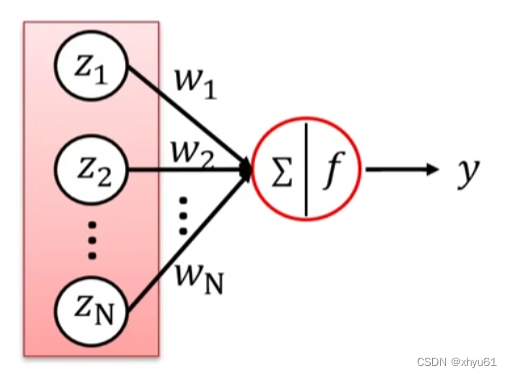
一个神经元,其输入为 z 1 , z 2 , ⋯ , z N z_1,z_2,\cdots,z_N z1,z2,⋯,zN,这 N N N个输入是独立同分布的;其权值为 w 1 , w 2 , ⋯ , w N w_1,w_2,\cdots,w_N w1,w2,⋯,wN,它们也是独立同分布的,且 w w w和 z z z是独立的;其激活函数为 f f f;其最终输出 y y y的表达式:
y = f ( w 1 ∗ z 1 + w 2 ∗ z 2 + ⋯ + w N ∗ z N ) y=f(w_1*z_1+w_2*z_2+\cdots+w_N*z_N) y=f(w1∗z1+w2∗z2+⋯+wN∗zN)
目标:使网络各层的激活值和局部梯度的方差在传播过程中尽量保持一致,即寻找 w w w的分布使得输出 y y y与输入 z z z的方差一致。
w 1 , w 2 , ⋯ , w N w_1,w_2,\cdots,w_N w1,w2,⋯,wN独立同分布, z 1 , z 2 , ⋯ , z N z_1,z_2,\cdots,z_N z1,z2,⋯,zN独立同分布,随机变量 w w w和 z z z独立,且均值都为 0 0 0。令 y = w 1 z 1 + w 2 z 2 + ⋯ + w N z N y=w_1z_1+w_2z_2+\cdots+w_Nz_N y=w1z1+w2z2+⋯+wNzN,根据概率统计知识我们有:
V a r ( w i z i ) = E [ w i ] 2 V a r ( z i ) + E [ z i ] 2 V a r ( w i ) + V a r ( w i ) V a r ( z i ) Var(w_iz_i)=E[w_i]^2Var(z_i)+E[z_i]^2Var(w_i)+Var(w_i)Var(z_i) Var(wizi)=E[wi]2Var(zi)+E[zi]2Var(wi)+Var(wi)Var(zi)
证明:
若 X X X独立同分布,则有 V a r ( X ) = E [ X 2 ] − E [ X ] 2 Var(X)=E[X^2]-E[X]^2 Var(X)=E[X2]−E[X]2
若 X , Y X,Y X,Y相互独立,则有 E [ X Y ] = E [ X ] E [ Y ] E[XY]=E[X]E[Y] E[XY]=E[X]E[Y]
等式左侧有:
V a r ( w i z i ) = E [ w i 2 z i 2 ] − E [ w i z i ] 2 = E [ w i 2 ] E [ z i 2 ] − E [ w i ] 2 E [ z i ] 2 Var(w_iz_i)=E[w_i^2z_i^2]-E[w_iz_i]^2=E[w_i^2]E[z_i^2]-E[w_i]^2E[z_i]^2 Var(wizi)=E[wi2zi2]−E[wizi]2=E[wi2]E[zi2]−E[wi]2E[zi]2
等式右侧也通过上述两个式子展开后发现和左侧相等。
通常我们有 E [ w i ] = E [ z i ] = 0 , V a r ( y ) = 1 E[w_i]=E[z_i]=0,Var(y)=1 E[wi]=E[zi]=0,Var(y)=1:
V a r ( y ) = V a r ( ∑ i = 1 N w i z i ) = ∑ i = 1 N V a r ( w i z i ) = ∑ i = 1 N ( E [ w i ] 2 V a r ( z i ) + E [ z i ] 2 V a r ( w i ) + V a r ( w i ) V a r ( z i ) ) = ∑ i = 1 N V a r ( w i ) V a r ( z i ) = n V a r ( w i ) V a r ( z i ) \begin{aligned} Var(y)&=Var(\displaystyle\sum\limits_{i=1}^N w_iz_i) \\ &=\displaystyle\sum\limits_{i=1}^N Var(w_iz_i) \\ &=\displaystyle\sum\limits_{i=1}^N (E[w_i]^2Var(z_i)+E[z_i]^2Var(w_i)+Var(w_i)Var(z_i)) \\ &=\displaystyle\sum\limits_{i=1}^N Var(w_i)Var(z_i) \\ &=nVar(w_i)Var(z_i) \end{aligned} Var(y)=Var(i=1∑Nwizi)=i=1∑NVar(wizi)=i=1∑N(E[wi]2Var(zi)+E[zi]2Var(wi)+Var(wi)Var(zi))=i=1∑NVar(wi)Var(zi)=nVar(wi)Var(zi)
不难看出,当 V a r ( w i ) = 1 N Var(w_i)=\frac{1}{N} Var(wi)=N1时, y y y的方差与 z z z的方差一致。
于是便有了Xavier初始化。
网络结构:10个隐层,1个输出层,每个隐层包含500个神经元,使用tanh激活函数。
随机初始化方式:权值采样自 N ( 0 , 1 / N ) N(0,1/N) N(0,1/N)的高斯分布, N N N为输入的神经元个数。
可以发现,达到目的:每层神经元激活值的方差基本相同。

7.4 He初始化
当把网络结构中激活函数改成ReLU函数时,使用Xavier初始化有:

此时的效果并不好。
推荐使用He初始化方法,即在Xavier初始化方法基础上仅修改随机初始化方式:权值采样自 N ( 0 , 2 / N ) N(0,2/N) N(0,2/N)的高斯分布。

综上,Sigmoid函数、tanh函数使用Xavier初始化,ReLU函数、Leakly ReLU函数使用He初始化。
7.5 批归一化
前面介绍的方法采取的思路如下:
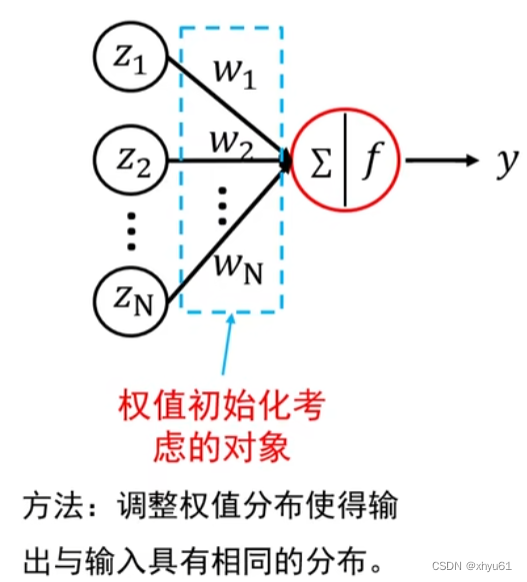
批归一化采取全新的思路,即直接对神经元的输出进行批归一化。
小批量梯度下降算法回顾:每次迭代时会读入一批数据,比如32个样本;经过当前神经元后会有32个输出值 y 1 , y 2 , ⋯ , y 32 y_1,y_2,\cdots,y_{32} y1,y2,⋯,y32。
批归一化操作:对32个输出进行减均值除方差操作;可保证当前神经元的输出值的分布符合0均值1方差。
如果每一层的每个神经元进行批归一化,就能解决前向传递过程中信号消失的问题。
批归一化与梯度消失

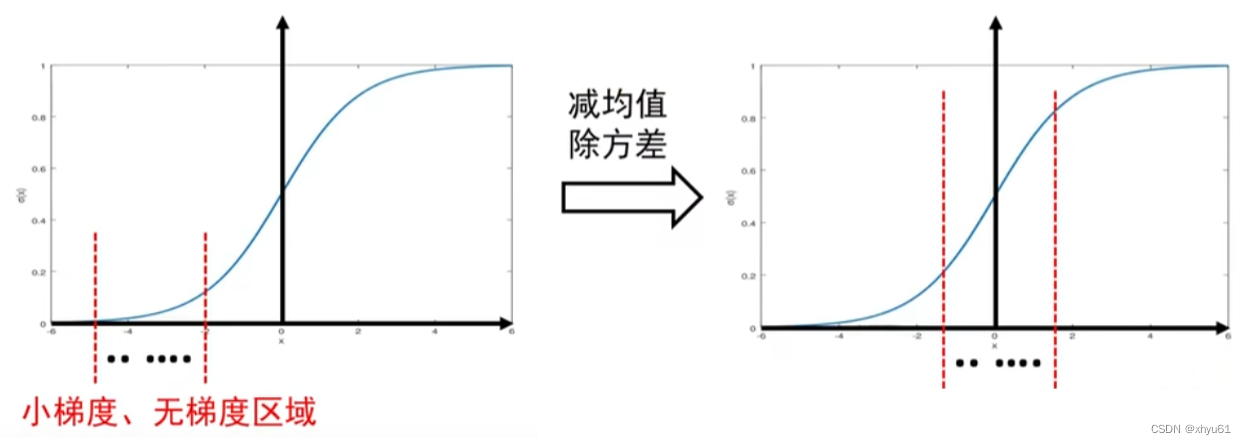
批归一化算法:
输入: B = { x 1 , ⋯ , x m } \mathcal{B}=\{x_1,\cdots,x_m\} B={ x1,⋯,xm};
学习参数: γ \gamma γ, β \beta β
输出: { y 1 , ⋯ , y m } \{y_1,\cdots,y_m\} { y1,⋯,ym}
1.计算小批量均值: μ B ← 1 m ∑ i = 1 m x i \mu_{\mathcal{B}}\leftarrow \frac{1}{m} \displaystyle\sum\limits_{i=1}^m x_i μB←m1i=1∑mxi
2.计算小批量方差: σ B 2 ← 1 m ∑ i = 1 m ( x i − μ B ) 2 \sigma_{\mathcal{B}}^2 \leftarrow \frac{1}{m} \displaystyle\sum\limits_{i=1}^m (x_i-\mu_{\mathcal{B}})^2 σB2←m1i=1∑m(xi−μB)2
3.归一化: x ^ i ← x i − μ B σ B 2 + ϵ \hat{x}_i \leftarrow \frac{x_i-\mu_{\mathcal{B}}}{\sqrt{\sigma_{\mathcal{B}}^2+\epsilon}} x^i←σB2+ϵxi−μB
4.平移缩放: y i ← γ x ^ i + β y_i \leftarrow \gamma \hat{x}_i +\beta yi←γx^i+β
问 输出的0均值1方差的正态分布是最有利于网络分类的分布吗?
答 根据对分类的贡献自行决定数据分布的均值与分差。
问 单张样本测试时,均值和方差怎么设置。
答 来自于训练中。累加训练时每个批次的均值和方差,最后进行平均,用平均后的结果作为预测时的均值和方差。
8 过拟合
机器学习的根本问题是优化和泛化的问题。
优化——是指调节模型以在训练数据上得到最佳性能。
泛化——是指训练好的模型在前所未见的数据上的性能好坏。
训练初期
优化和泛化是相关的:训练集上的误差越小,验证集上的误差也越小,模型的泛化能力逐渐增强。
训练后期
模型在验证集上出现的错误率不在降低,转而开始变高。模型出现过拟合,开始学习仅和训练数据有关的模式。
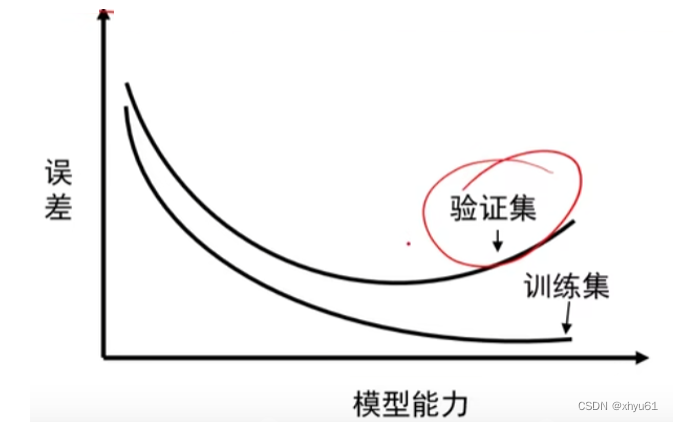
8.1 过拟合
出现过拟合,得到的模型在训练集上的准确率很高,但在真实的场景中识别率却很低。
过拟合是指学习时选择的模型所包含的参数太多,以至于出现这一模型对已知数据预测得很好,但对于未知数据预测得很差的现象。这种情况下模型可能只是记住了训练集数据,而不是学习到了数据特征。
应对过拟合
最优方案——获取更多的训练数据
次优方案——调节模型允许存储的信息量或者对模型允许存储的信息加以约束,该类方法也称为正则化。
正则化的方法有两种:
- 调节模型大小
- 约束模型权重,即权重正则化(常用的有L1、L2正则化)
回顾正则化:
L = 1 N ∑ i L i ( f ( x i , W ) , y i ) + λ R ( W ) L=\frac{1}{N}\displaystyle\sum\limits_{i} L_i(f(\mathbf{x}_i,\mathbf{W}),y_i)+\lambda R(\mathbf{W}) L=N1i∑Li(f(xi,W),yi)+λR(W)
式中 λ R ( W ) \lambda R(\mathbf{W}) λR(W)为正则项。
其中我们将 1 N ∑ i L i ( f ( x i , W ) , y i ) \frac{1}{N}\displaystyle\sum\limits_{i} L_i(f(\mathbf{x}_i,\mathbf{W}),y_i) N1i∑Li(f(xi,W),yi)称作数据损失,模型预测需要和训练集相匹配;将 λ R ( W ) \lambda R(\mathbf{W}) λR(W)称作正则损失,防止模型在训练集上学习得“太好”。
R ( W ) R(\mathbf{W}) R(W)是一个与权值有关,跟图像无关的函数。
λ \lambda λ是一个超参数,控制着正则损失在总损失中所占的比重。
L2正则项: R ( W ) = ∑ k ∑ l W k , l 2 R(\mathbf{W})=\displaystyle\sum\limits_{k}\displaystyle\sum\limits_{l} W_{k, l}^2 R(W)=k∑l∑Wk,l2
L2正则损失对于大数值的权值向量进行严厉惩罚,鼓励更加分散的权重向量,使模型倾向于使用所有输入特征做决策,此时的模型泛化性比较好。对于分界面:不会生成过于复杂的分界面,会尽量使分界面变得平滑。
8.2 欠拟合
欠拟合是指模型描述能力太弱,以至于不能够很好地学习到数据中的规律。产生欠拟合的原因通常是模型过于简单。
8.3 随机失活 (Dropout)
随机失活:让隐层的神经元以一定概率不被激活。
实现方式:训练过程中,对某一层使用Dropout,就是随机将该层的一些输出舍弃(输出值设置为0),这些被舍弃的神经元就好像被网络删除了一样。
随机失活比率 (Dropout Ratio):是被设为0的特征所占的比例,通常在0.2~0.5范围内。
例:假设某一层对给定的输入样本的返回值应该是向量: [ 0.2 , 0.5 , 1.3 , 0.8 , 1.1 ] T [0.2,0.5,1.3,0.8,1.1]^T [0.2,0.5,1.3,0.8,1.1]T,使用Dropout后,这个向量会有几个随机的元素变成 [ 0 , 0.5 , 1.3 , 0 , 1.1 ] T [0,0.5,1.3,0,1.1]^T [0,0.5,1.3,0,1.1]T。
问 为什么随机失活能够防止过拟合?
解释1 随机失活使得每次更新梯度时参与计算的网络参数减少了,降低了模型容量,所以能防止过拟合。
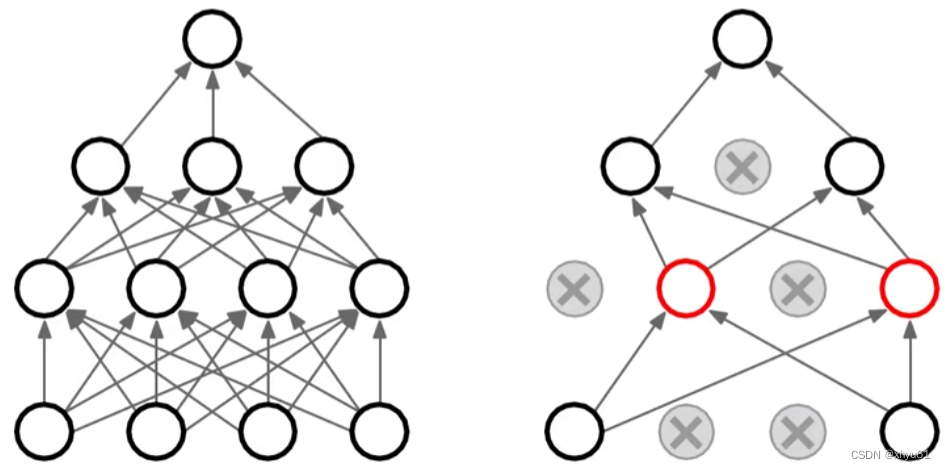
解释2 随机失活鼓励权重分散,从这个角度来看随机失活也能起到正则化的作用,进而防止过拟合。
对于一层的神经元,其需要上一层的所有神经元的学习结果。如果上一层中的每个神经元只学习一种特征,那么当这些神经元发生随机失活时,本层的神经元会丢失信息。因此,每一个神经元需要存储更多的信息防止信息流动失败。
解释3 Dropout可以看作模型集成。
每次失活后剩下的网络可以看做一个小的模型,而不同的失活状态导致生成的模型不同,最后输出的结果会产生多种小模型学习后的结果,相当于集成了多种小型模型。 从这个角度来看,随机失活也可以使模型变得更加稳定。
存在的问题


9 超参数
超参数:
- 网络结构——隐层神经元个数,网络层数,非线性单元选择等
- 优化相关——学习率、dropout比率、正则项强度等
9.1 学习率

- 学习率过大,训练过程无法收敛
- 学习率高(偏大),在最小值附近震荡,达不到最优
- 学习率过低,收敛时间较长
- 学习率适中,收敛快、结果好
9.2 超参数优化方法
每组实验选取过拟合之前最优的那一刻中最低的损失值进行比较。
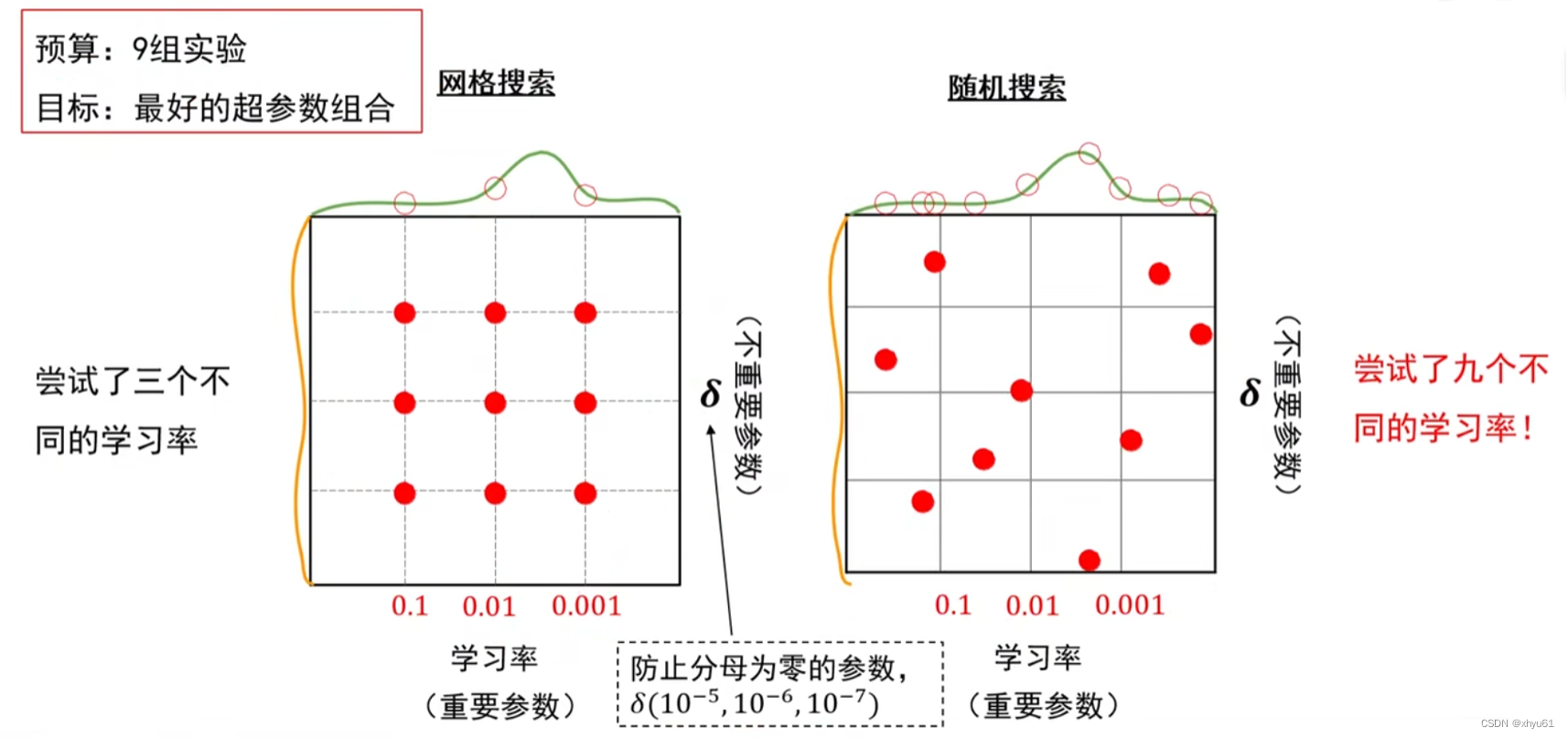
网格搜索法
①每个超参数分别取几个值,组合这些超参数值,形成多组超参数;
②在验证集上评估每组超参数的模型性能;
③选择性能最优的模型所采用的那组值作为最终的超参数。
随机搜索法
①参数空间内随机取点,每个点对应一组超参数;
②在验证集上评估每组超参数的模型性能;
③选择性能最优的模型所采用的那组值作为最终的超参数的值。
更倾向于随机搜索法,因为这种方法,我们可以尝试9个超参数
9.3 超参数搜索策略
粗搜索
利用随机法在较大范围里采样超参数,训练一个周期,依据验证集正确率缩小超参数范围。

精搜索
利用随机法在前述缩小的范围里采样超参数,运行模型五到十个周期,选择验证集上精度最高的那组超参数。
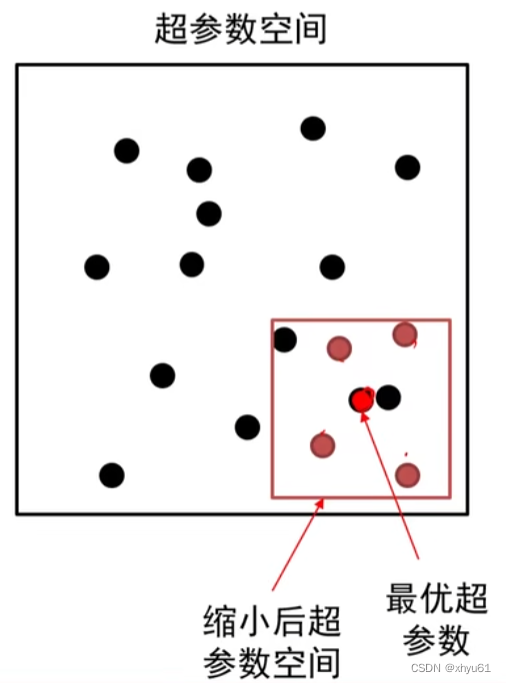
9.4 超参数的标尺空间
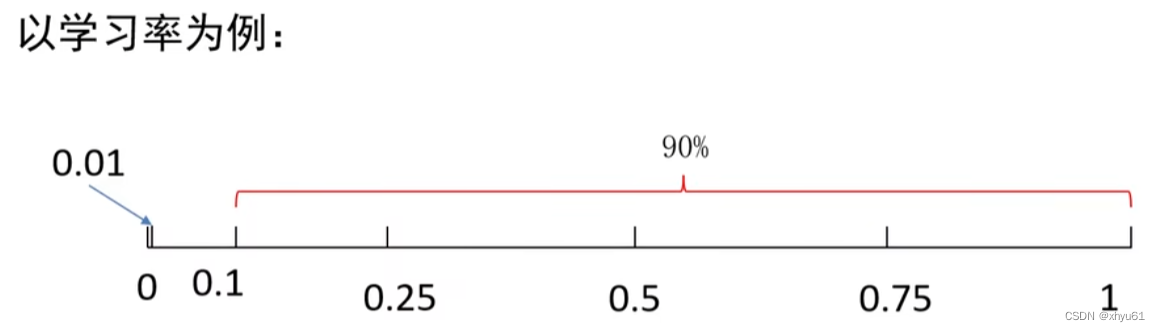
最优的值在[0.0001,1]之间,我们如何采样?
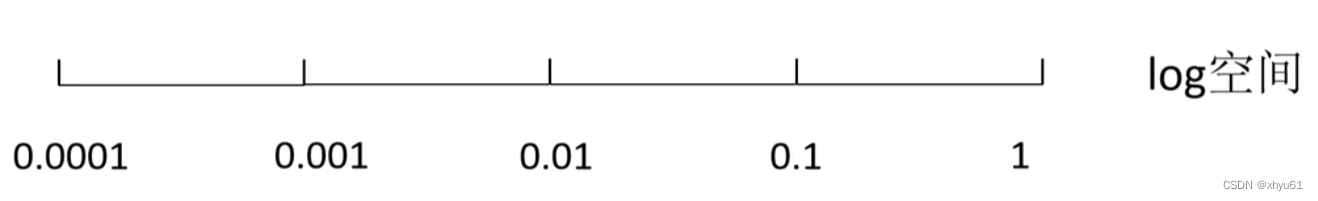
对于学习率、正则项强度这类超参数,在对数空间上进行随机采样更合适!