Abstract

语义 GP 是在遗传进化过程中引入语义意识的一种很有前途的方法。本文提出了一种新的基于动态目标的语义 GP 方法 (SGP-DT)，将搜索问题划分为多个 GP 运行。每次运行中的演化由基于残差的新(动态)目标引导。为了得到最终解，SGP-DT 采用线性缩放的方式对每次运行的解进行合并。SGP-DT 提出了一种新的方法来产生不依赖于经典交叉的子代。这种方法与线性缩放之间的协同作用使得最终解具有较低的近似误差和计算成本。我们在八个著名的数据集上评估 SGP-DT，并与最先进的进化技术 $\epsilon$ -lexicase 进行比较。 SGP-DT 取得了较小的 RMSE 值，平均比 $\epsilon$ -lexicase 小 23.19%。

1 Introduction

最近，研究人员成功地将语义方法应用于不同领域的遗传编程 (Genetic Programming，SGP)，取得了很好的效果 [1 , 2 , 3]。而经典的 GP 算子(例如：选择、交叉和变异) 作用于句法层面，一味地针对个体的语义(行为)，SGP 的关键思想是应用语义评价 [1]。更具体地说，经典的 GP 算子忽略了子代的行为特征，只注重提高个体的适应度。不同的是，SGP 在进化过程中使用了更丰富的反馈，其中包含了语义意识，具有提高遗传编程能力的潜力 [1]。

在本文中，我们考虑符号回归域，并由此假设训练样本的可用性为(定义为 $m$ 对输入和期望输出)。遵循最流行的 SGP 方法 [1]，我们打算将 “语义” 作为程序在训练样本上的输出值集合 [4]。这样的方法在依赖个体对训练案例的评价的演化过程中获得了更丰富的反馈. 更正式地，个体 $\mathcal{I}$ 的语义是对训练案例的 $m$ 个输入的响应向量 $sem(\mathcal{I}) =〈y_1，y_2，· · ·，y_m〉$ 。令 $sem(\hat{y}) =〈\hat{y}_1，\hat{y}_2，· · ·，\hat{y}_m〉$ 表示目标(定义在训练集中)的语义向量，其中 $\hat{y}_1，\hat{y}_2，· · ·，\hat{y}_m$ 为期望输出。SGP 定义了语义空间 [1]，该空间用一个度量来刻画个体 $sem(\mathcal{I})$ 和目标 $sem(\hat{y})$ 的语义向量之间的距离。SGP 通常依靠这样的距离来计算适应度分数，从而形成单峰适应度景观，通过构建避免了局部最优 [5]。

SGP 的有效性依赖于能够在语义空间中向全局最优移动的 GP 算子的可用性。语义算子的一个例子是 Moraglio 等 [5] 提出的几何交叉算子。它产生一个语义向量位于语义空间中连接父代的连线上的子代。因此，它保证了子代不会比父代的最差 [5]。然而，这种交叉算子的主要缺点是产生具有指数增长的个体(即指数膨胀) [5、1]。为了避免指数膨胀，研究人员提出了该算子的变体，以最小化膨胀 [2]，但代价是放弃了非恶化交叉操作的重要保证。

在本文中，我们提出了一种新的 SGP 方法，称为 SGP-DT (基于动态目标的语义遗传编程)，它最小化了指数膨胀问题，同时给出了子代退化的一个界。 SGP-DT 将搜索问题分解为多个 GP 运行。每次运行由不同的动态目标引导，SGP-DT 在每次运行时根据上一次运行的残差进行更新。然后，SGP-DT 将每次运行的结果合并为一个 “优化” 的最终解。

简言之，SGP-DT 的工作原理如下：SGP-DT 根据可用预算运行 GP 算法(见算法 1) 固定次数 ( $N_{ext}$ )。我们称这些运行为外部迭代。相对于 GP 算法执行进化个体的内部迭代(即,世代)。每个 GP 运行执行固定数量的内部迭代并返回一个模型(即最佳方案)，我们称之为 Partial Model。下一次外部迭代使用修改的训练集运行 GP 算法，其中 SGP-DT 用上一次迭代返回的部分模型的残差替换 $m$ 个期望输出 $\hat{y}_i =〈\hat{y}_1，\hat{y}_2，· · ·，\hat{y}_m〉$ 。即 $sem(\mathcal{I}_i$ ) 与 $sem(\hat{y}_i-1)$ 之差，其中 $\mathcal{I}_i$ 为第 $i$ 次迭代时的部分模型。因此，在每次外部迭代时，适应度函数对个体进行不同的评价(因为适应度函数基于不同的训练集进行预测)。因此，每个部分模型关注的是问题的不同部分，即对适应度值影响最大的部分。因此，我们的方法会导致动态目标在每次包含语义信息的外部迭代中发生变化。SGP-DT 通过线性组合 $\sum_{i=0}^{N_{ext}} a_i + b_i·\mathcal{I}_i$ ，在下一次迭代后得到最终解。使用线性缩放有一个关键的优点。Keijzers 证明线性缩放给出了被线性缩放的生成个体的误差上界。因此，SGP-DT 在每次内部和外部迭代时都需要对子代的恶化进行约束。

为减少指数膨胀问题，SGP-DT 仅依靠经典变异算子进行内部 GP 迭代。它不依赖于任何形式的交叉，既不是几何的也不是经典的，从而避免了它们的根本局限。几何交叉会导致指数膨胀，而经典交叉由于在随机点交换随机函数而减少了获得适应度改进的机会 [7]。尽管没有交叉，SGP-DT 隐式地重组了不同的函数，类似于几何交叉 [5]。这是因为，每个部分模型都关注一个不同特征的问题，即适应度函数被公认为重要的(在那次迭代)。这使得搜索更加高效，因为进化一次只关注单一特征，而不改变其他(已经优化的)特征。

我们在八个著名的回归问题上评估了我们的方法。我们将 SGP-DT 与 Efron 等 [8] 的 lasso 最小二乘回归技术两种基线进行比较；La Cava 等 [9] 提出了一种最先进的 SGP 方法。结果表明，我们的方法在 50 次运行上获得了中值 RMSE，平均比 lasso 和 $\epsilon$ -lexicase 分别小 51.47% 和 23.19%。此外，SGP-DT 比 $\epsilon$ -lexicase (平均 4.81×)需要少 9.26 倍的树计算。

2 Methodology

算法 1 概述了 SGP-DT 方法。给定训练案例的独立变量 $(\bar{x})$ 和因变量 ( $\hat{y}$ ) 的值，以及外部迭代次数 (N $_{ext}$ ) 和内部迭代次数 (N $_{int}$ )，返回最终解(final Model)。

SGP-DT 考虑具有通常的非终端符号：+，-，·，/ (受保护的除法)，ERC (在 -1 和 1 之间)的树形个体。此外，SGP-DT 考虑了两个数之间分别返回最小值和最大值的函数 Min 和 Max。增加后两个符号的理由是注入不连续性，使线性组合更具有适应性。虽然被保护的分割也以渐近线的形式增加了不连续性，但这种不连续性往往会促进 [6、10] 的过拟合。利用 Min 和 Max 函数，我们引入了不受保护划分限制的有效不连续替代。

算法 1 为验证(第 1~3 行)保留一部分训练案例。SGP-DT 将使用这样的验证集来构造最终解(第 22 行)。第 4~5 行用 $\hat{y}$ 初始化当前目标，用空列表初始化最佳模型列表。第 6 行开始外部循环，它将 $\mathcal{P}$ 重新赋值给一个新的随机生成的种群，并使用 half and half 方法产生新的种群(算法 1 的函数 GET-RANDOM-INITIAL-POPULATION)。每一个开始采用新种群进行外部迭代，缓解了过拟合问题。事实上，已经进化的个体的句法结构可能过于复杂，无法适应新的适应度景观或在看不见的数据上进行泛化。为了进一步减少过拟合和适应度评价的代价， SGP-DT 使用低复杂度的(即少数节点)个体生成初始种群。

在第 8 行，SGP-DT 开始 N $_{int}$ 内部迭代，类似于经典的 GP，但增加了线性缩放和没有交叉。在第 11 行计算 $\mathcal{P}$ 中每个个体 $\mathcal{I}$ 的适应度之前，第 10 行执行 $\mathcal{I}$ 的线性缩放 [6]。线性缩放的优点是可以转换个体的语义，使其与当前目标的潜在契合度达到更好：我们不需要等待 GP 产生一个达到相同结果的部分模型 [6]。因此，线性缩放减少了外部和内部迭代的次数。更少的迭代意味着具有更简单结构复杂度和更少计算成本的种群。降低解的复杂度可以减少过拟合 [11]。

线性缩放还有一个重要的性质：它给出了误差的一个上界 [6]。回想一下， SGP-DT 考虑了动态目标上的误差，这些误差是变化的在每次迭代时(在第一次迭代时动态目标为 $\hat{y}$ .为了利用这种情况，我们提出了一个基于这个上界的适应度函数。根据 Keijzer[6]，我们计算个体 $\mathcal{I}$ 的线性放缩：

$\mathcal{I}_{ls} = a + b · \mathcal{I}$
$\bar{\hat{y}} - b · \bar{y}$
$\frac{\sum_{i=1}^n[(\hat{y}_i - \bar{\hat{y}}) · (y_i - \bar{y})]}{\sum_{i=1}^n[(y_i - \bar{y})^2]}$

我们定义如下个体 $\mathcal{I}$ 的适应度函数：
$fitness{(\mathcal{I})} = \sigma^2(sem(\mathcal{I_{ls}(\bar{x})}) - \hat{y})\tag{3}$

其中 $sem(\mathcal{I_{ls}(\bar{x})})$ 为当前个体带入训练集 $\bar{x}$ 后的值向量，该函数的基本原理是 $\mathcal{I_{ls}}$ 的均方误差 (Mean Square Error，MSE) 以当前目标的方差 ( $\sigma^2$ ) 作为上界 [12]：
$\frac{\sum^m_{i=0}(y_i - \hat{y}_i)^2}{m} \leq \sigma^2(\hat{y})\tag{4}$

其中 $m$ 为训练样本数 $(y)$ 。

在每次新的外部迭代中，残差成为新的目标 (第 21 行)。即本文动态目标的原因
$\hat{y} - sem(\mathcal{I}_{ls}^*(\bar{x}))\tag{5}$

式中 $sem(\mathcal{I}_{ls}^*(\bar{x}))$ 为当前迭代时最优个体的评价，我们称之为部分模型。

不等式 4 并不能保证外部迭代收敛到较低的 MSE，因为我们不知道 $σ^2(error) ≤ σ^2(\hat{y})$ ，其中 $target-sem(\mathcal{I}_{ls}^*(\bar{x}))$ 。因此，通过优化方程 3 所示误差的方差，我们直接作用于最小化上界，使得下一次外部迭代可以从下界中获益。

在第 17- 19 行，算法 1 运行一个经典的 GP 算法，没有交叉，只使用变异。我们使用基于树的变异算子，因为 SGP-DT 使用树作为个体的句法结构。该算子从随机选择的节点随机生成一棵子树。为了增加线性缩放的协同性，我们在变异过程中设置了两个约束条件。首先，节点选择偏向于树的叶子，使得变异后的树不会与原始语义(局部性原则)产生太大的发散。产生接近树的原始语义的变异保留了线性缩放后执行的选择的有效性。因此，我们只允许微小的变化来提高适应度。其次，出于同样的原因，变异偏向于将选择的节点替换为深度有限的子树。注意，我们决定不限制个体的最大尺寸(树中节点的数量)或深度。通过这样做，GP 可以为手头的问题生长并选择合适的解复杂度。这两个约束有助于我们在不妨碍 SGP-DT 有效搜索竞争个体的情况下缓解过拟合和膨胀问题。由于线性缩放有助于 GP 找到有用的个体(得益于上界)。此外，额外的外部迭代将进一步细化尚未解决的问题的其他方面。

我们决定在内部迭代中排除经典的交叉算子，因为一些研究人员就交叉的有效性与 GP 的模块化问题进行了争论 [13]。有一种共识是，一个有效的 GP 算法需要一个交叉，在个体的结构 [7、2、14] 中，保留个体之间交换的部分的语义，尊重有用功能的边界。根据 Mc Phee 等 [4] 和 Ruberto 等 [11] 的研究，在处理布尔型和实值型符号回归域时，大多数经典的交叉算子在程序语义中并没有获得有意义的变异(或任何变化在所有)。主要问题是经典的交叉算子在交叉过程中交换的个体的构建块之间不保留共同的上下文 [4]，这对于增加获得具有语义意义的后代的机会是很重要的 [14]。Poli 和 Langdon 利用单点交叉算子 [7] 提出了确定公共上下文的思想。但如何识别树结构之间有意义的共同背景仍然是一个开放性问题。

相反，SGP-DT 依靠部分模型(即每次外部迭代时的最适合个体,第 12 行算法 1)的线性组合以及在 GP 运行过程中选择和变异个体的特定机制来交换个体间的功能。鉴于此，我们排除了存在这些语义重组备选项的交叉算子。为了在个体之间进行有效的功能交换，我们需要：(i) 保持积木语义 (ii) 保持积木的上下文 (iii) 使功能交换指向产生新的和有趣的语义。SGP-DT 通过 (i) 将每个积木块映射到单个局部模型(这将避免块的任意碎裂)来实现这些目标；(ii) 保留构建块的上下文，因为在我们的场景中，之前迭代得到的部分模型代表上下文；(iii) 仅使用变异，促进了种群的多样性。尽管没有交叉点，但 SGP-DT 交换构建块，因为每个部分模型都是构建块。与经典的交换随机片段的交叉方式不同，SGP-DT 通过对线性缩放的部分模型求和得到最终模型。这种方法使得功能的交换更加有效，因为每个部分模型(构建块)都表征了一个特定的功能。

当 SGP-DT 结束所有外部迭代时，第 6 行的 for-loop 终止。我们决定不引入基于适应度改进停滞的不同停止准则。这是因为很难预测在未来的迭代中适应度是否不会逃脱停滞。在所有的外部迭代之后，在算法 1 的第 22 行进行验证选择的函数返回将被组合到最终解中的部分模型。此类模型选取如下。验证输入每次内部迭代后收集的最佳个体(模型)的有序序列(第 14 行算法 1)和第 1 行得到的验证集( $\bar{x}_{val}$ 和 ( $\bar{y}_{val}$ ))。值得注意的是，SGP-DT将计算得到的线性缩放参数( a、b方程 (2))) 保存在第 10 行，在验证和测试阶段不重新计算。在内部，验证扫描序列模型并逐步计算 MSE 对验证集上的个体进行评估，寻找序列中 MSE 最小的点。SGP-DT 在固定窗口大小下利用验证集误差的滚动均值寻找最小的 MSE，以最小化短期波动。函数 validate-and-select 返回 MSE 最小之前产生的部分模型的序列 (bestModels)。这样的序列代表了动态目标的转化链。如果 SGP-DT 在内部迭代过程中得到了 MSE 最小的模型，则在 bestModels 的末尾追加该个体。算法 1 的第 23 行通过求和 bestModels 中的所有模型来计算最终模型。

3 Related Work

本部分将 SGP-DT 的相关工作分为三组。每一组都是指与 SGP-DT 的主要特征相关的技术：(i) 具有动态或语义目标，(ii) 使用线性组合或几何算子，(iii) 使用迭代方法处理残差。

动态或语义目标 Krawiec等 [15] 和 Liskowski 等[16] 提出的 GP 技术提出了考虑个体与训练集交互的语义方法。这些方法对这些相互作用进行聚类，以获得多目标 GP 的新目标。

Otero 等人提出了一种具有动态目标的方法，在最终的布尔树中结合中间解 [17]。该技术从训练样本中逐步淘汰从当前中间解中完美预测的样本，并且只在布尔域中运行。

Krawiec 和 O’Reilly [18] 提出了一种 GP 方法，在计算训练案例时显式地建模解决方案的语义行为。

Krawiec and O’Reilly [18] 提出的 BPGP 在计算训练案例的过程中显式地建模解决方案的语义行为。BPGP 提出了一种通过将随机选择的子树替换为随机子树来变异个体的算子。根据 Krawiec and O’Reilly 的定义，这种"类变异" [18]算子是一种"交叉形式"。我们认为，这与我们的设计选择是完全放弃交叉，而是在种群中变异的备选方案中进行选择在原理上是相似的。然而，Krawiec and O’Reilly 仍然使用传统的交叉和这种新的变异 [18]。

我们不同于所有这些技术，因为我们建立我们的解决方案逐步结晶的中间成果。这些方法大多在搜索过程中使用辅助目标，并使用单个 GP 运行。相反， SGP-DT 在后续的 GP 运行中使用非预定数量的目标。Otero 等 [17] 的方法是唯一一个逐步建立解决方案的方法，但它使用的策略仅适用于布尔树。

线性组合 MRGP[19] 利用多元线性回归对子程序(子树)的语义进行组合，形成个体的语义。

Ruberto et al 提出了 ESAGP [20]，通过依赖误差空间中两个"最优对齐"个体之间的特定线性组合来推导目标语义。利用这种几何对齐性质，Vanneschi et al 提出了 NA-GP [21]，它在属于同一个体的两条对齐的染色体之间进行线性组合。

Gandomi 等人提出了 MGGP[22]，其中每个个体由多棵树组成。MGGP 通过树语义的线性组合产生最终解，通过经典的最小二乘法从训练数据中得到系数的值。但线性组合中的树木数量是固定的，适应度景观不是动态的。

Moraglio 等人提出了几何语义 GP(Geometric Semantic GP，GSGP )交叉算子 [5]，利用线性组合保证子代不劣于父代的最差子代。遗憾的是，GSGP 存在指数膨胀问题，需要很多代才能收敛，尤其是当目标不在初始种群所张成的凸包中时 [5]。

值得注意的是，第二组中描述的所有方法都使用一次运行来搜索最终的解决方案。与 SGP-DT 不同的是，它们提前(唯一的例外是 GSGP ,但它存在指数膨胀问题)固定了组件数量。此外，第一组和第二组中的所有技术都有一个静态目标，因此它们在不重新初始化的情况下不断进化种群。这就限制了当种群在后代收敛时遗传替代物的多样性。相反，SGP-DT 具有动态目标，在每次内部迭代(见算法 1)时以一个新的种群开始。

基于残差的迭代方法 序列符号回归 (sequential Symbolic Regression，SSR) [23] 使用交叉算子 GSGP [5]，使用类似于经典残差方法的语义距离对目标进行迭代变换。然而，与经典 GP 方法相比，未发现统计学差异(在错误上) [23]。与 SGP-DT 不同，SSR 采用最小二乘法考虑未优化线性组合的残差。虽然 SSR 克服了指数膨胀，但削弱了使用残差的优势。

Medernach 等人提出了类似于 SGP-DT 的 wave 技术 [24、25]，使用相同的残差定义(公式 5 )执行多个 GP 游程，并通过对中间模型求和得到最终模型。 wave 通过对系统参数(例如,种群规模、内部迭代次数等)的设置进行"模糊化"和交替使用线性缩放得到一个短且异构的 GP 游程序列。然而，SGP-DT与波浪有很大不同。波浪的非均匀性通过模拟快速变化的 [24、25] 的周期来模拟这种动态演化环境。这种方法的有效性需要系统参数的特定组合才能收敛到一个较好的解。由于可能的系统参数空间巨大，寻找这样的组合往往需要大量的迭代次数 [24、25]。相反，SGP-DT 以一种新颖的方式引导进化，在不探索系统参数可能组合的巨大空间的情况下，逐步进化最终解决方案的构建块。

该组的所有技术使用残差与 SGP-DT不同。而且，它们依赖于经典或几何的交叉。反过来说，SGP-DT 的一个关键新颖之处就是避免了交叉。

4 Evaluation

数据集 我们在 8 个著名的回归问题数据集上进行了实验，这些数据集已经用于评估第 3 节 [9、19、21、22、24、25] 中讨论的大部分技术。表 1 给出了每个数据集的名称、属性个数和实例个数。对于 uball5d³，我们沿用了 Cava 等 [28] 的相同构型。

4.1 Methods

我们将 SGP-DT 与两种技术 lasso 和 $\epsilon$ -lexicase )以及 SGP-DT 的两种变体 (DT-EM 和 DT-NM) 进行了比较。

lasso SGP-DT 和 lasso[8] 都使用最小二乘回归方法对解分量进行线性组合。更具体地说，lasso 使用模型系数的 $\ell_1$ 范数在最小二乘回归中引入正则化惩罚，并使用调节参数λ来指定该正则化的权重 [8]。我们依赖于 Efron 等[8] 的 lasso 实现，该实现通过交叉验证自动选择 λ。

$\epsilon$ -lexicase 这种进化技术适用于连续域的lexicase选择算子 [9]。 $\epsilon$ -lexicase 选择背后的思想是促进在训练集中样本的独特子集上表现良好的候选解决方案，从而维护和促进解决方案的不同构建块 [9]。每个父代选择开始于对训练案例和选择池(即人口)中的解进行随机排序。如果个体在当前训练样本上不在池中性能最好的一个小阈值( )内，则迭代地从选择池中移除. 当除一个个体外的所有个体都留在池中，或者直到所有个体都有绑定性能时，选择过程终止。在后一种情况下，选择一个随机的。最近奥热霍夫斯基等人的研究表明- lexicase [ 9 ]优于许多GP启发的算法[ 29 ]。我们依赖于- lexicase的公开实现ellyn4，它使用随机爬山来调整每个生成个体的标量值。它还依赖于从训练数据中25 %的验证保留来从二维Pareto存档中选择最终的模型，该模型在进化过程中不断更新。两个维度分别是节点数量和适应度。

DT-EM 我们考虑 SGP-DT 的一个变种(称为 DT-EM)，它与 SGP-DT 的唯一区别是修改了适应度函数：

当 SGP-DT 的原始适应度函数最小化方程 3 中 MSE 的上界时，该函数直接最小化方程 6 中的 MSE。该变量有助于评估直接误差最小化相对于更定性和间接的误差度量的影响，例如方差 (σ²)。DT-NM 我们考虑了另一种称为 DT-NM 的变体，它排除了 Min 和 Max 非端点符号(作为与 SGP-DT 的唯一区别)，从而评估了不同间断类型在演化过程中的优势。

4.2 Evaluation setup

参照 Orzechowski et al 等 [29] 对 $\epsilon$ -lexicase的设置，我们将所有 4 种 GP 技术 (SGP-DT、 $\epsilon$ -lexicase、DT-EM、DT-NM) 设置为种群规模为1000，预算为 1000 代。每种技术在每个数据集上运行 50 个试次，25%的数据用于测试，75%的数据用于训练。

SGP-DT 及其两个变种具有相同的配置：在 20 个外部迭代 ( $N_{ext}$ = 20) 中划分 1000 代，因此内部迭代次数 ( $N_{int}$ ) 为 50。我们使用渐变的一半和一半初始化，最大深度为 4 个(算法 1 的第 7 行函数 GET-RANDOM-INITIAL-POPULATION。变异概率为 100%，变异算子生成的子树最大深度为 5。子树突变发生在叶片水平的概率为 70%。我们对树中的节点数量和树的深度没有设置限制。我们设置精英主义在每次内部迭代(算法 1 第 16 行的函数精英)时只保留最好的个体。通过抽取 10% 的训练案例(算法 1 第 1 行的函数分裂)得到验证集。滚动均值的固定窗口大小为 20。我们在初步调优阶段后选择了这种配置，并对所有的 8 个数据集保持统一。

4.3 Results and discussion

Errors’ Comparison 在前面的工作中，我们使用均方根误差 (RMSE) 来评估测试集的最终解决方案。表 2 的前五列显示了每种技术 50 个试验的 RMSE 中位数。表 2 的后四列表示 RMSE 中位数相对于竞争者技术⁵ 的百分比下降。正的百分比值意味着 SGP-DT 的 RMSE 中位数更低，而负的百分比值意味着最差的RMSE中位数。图 1 显示了 50 个 trial 的 RMSE 值的箱线图⁶。在比较我们执行的 RMSE 值时非参数两两 Wilcoxon 秩和检验，采用 Holm 校正进行多重检验，置信度为 95% ( p-value < 0.05 )。

⁵以 (( $M_T-M_D )) / M_T) · 100$ 计算，其中 $M_D$ 为 SGP-DT 的中值 RMSE， $M_T$ 为竞争技术之一
⁶由于可读性的原因，我们省略了 lasso 的 4 个外层、 $\epsilon$ -lexicase 的 13 个外层、SGP-DT 的 30 个外层、DT-NM 的 30 个外层和 DT-EM 的 35 个外层

SGP-DT 在所有数据集上都取得了比 lasso 更小的 RMSE，并且始终具有统计显著性。RMSE 中位数的下降幅度从 housing 的 9.06% 到 yacht (平均51.47%)的 88.67%。对于除(降低-4.48%)外的所有数据集，SGP-DT 的 RMSE 中位数均小于 $\epsilon$ -lexicase。这是 SGP-DT 和 $\epsilon$ -lexicase 唯一没有统计学意义的比较。RMSE 中位数的降低范围为 -4.48% 到 57.07%。这是一个令人瞩目的结果，考虑到 $\epsilon$ -lexicase 优于许多受 GP 启发的算法 [29]。与变体 DT-EM 相比，SGP-DT 在数据集 uball5d 和 yacht 上与 DT-EM 仅有统计学上的显著差异，下降百分比分别为 6.63% 和 20.45%。对于这样的数据集，SGP-DT 比 DT-EM 表现更好，表明我们的最小化上界的适应度函数取得了更好的最终解。SGP-DT 与 DT-NM 仅在airfoil、tower 和 uball5d 数据集上的中值 RMSE 差异具有统计学意义。在 airfoil* 和 tower 数据集上，SGP-DT 比 DT-NM 表现更好：分别下降 3.94% 和 10.12%。这意味着 Min 和 Max 非终端符号仅在这两个数据集中提供了优势。然而，图 1 表明，除了 uball5d 的差异在统计上显著为(降幅为 -7.87% )外，使用这种非终端符号并不会对其他任何数据集中的结果造成惩罚。

Error comparison with related work 遗憾的是，Wave [ 24、25]的实施并不公开，因此很难进行直接比较。我们从 GECCO 2016 论文 [25] 中提取了 4.1 (concrete)和 8.7 (yacht)两个公共主题的中值 RMSE。SGP-DT 的 RMSE 百分比中位数降低了 25.17% (concrete)和 75.12% (yacht)，参考值见表 2。值得注意的是，GECCO 论文中报告的计算成本与 SGP-DT 中的计算成本具有相同的数量级。

从 Vanneschi 等[21]的论文中，我们提取了在以下 GP 技术的数据集上的中值RMSE：10.44 (NA-GP [21])，8.1 (NA-GP-50 [21])，12.50 (GSGP[5])和 9.43 (GSGP-LS)。SGP-DT 分别降低了 37.64%、19.62%、47.92% 和 30.96%。这些结果只是指示性的，因为它们的评估设置与我们的不同。

Computational effort 为了评估演化技术的计算效率，我们决定不依赖于执行时间，因为它依赖于实现细节。取而代之的是评估节点总数(由于不是 GP 技术,该度量不适用于 lasso)。SGP-DT 和 $\epsilon$ -lexicase 都运行在节点上，SGP-DT 运行在树状数据结构上，而 $\epsilon$ -lexicase 运行在基于栈的数据结构上。根据 Ruberto 等人[11]，无论操作(例如,变异、适应度计算等)的目的是什么，我们都会在每次技术评估一个节点时统计一个节点操作。我们排除了线性缩放的计算工作量，因为它不对节点执行操作。然而，它的线性计算成本为 $\mathcal{O}( m · P)$ ，其中 $m$ 为训练集大小， $P$ 为种群大小。对于评估节点数的比较，我们使用 Wilcoxon 秩和检验和 Holm 校正进行多重检验，置信水平为 95% ( p值 < 0.05 )。检验表明，除在被试 uball5d 上与 SGP-DT 和 DT-NM 进行比较外，各对技术之间的比较均具有统计学意义。

表 3 报告了 GP 技术评估产生最终解决方案的节点中位数(在 50 次运行中)。表 3 后三列报告了 SGP-DT 与 $\epsilon$ -lexicase、DT-EM 和 DT-NM 的节点评价数量之比。大于(小于)的比率意味着 SGP-DT 评估的节点数较低(高)。与 $\epsilon$ -lexicase 相比，SGP-DT 减少了 4.01 × and 9.26 × 之间的节点评价量，在 8 个数据集中有 7 个数据的 RMSE 值显著优于 $\epsilon$ -lexicase。这一结果可以解释为：(i) SGP-DT 一次只计算整个解(部分模型)的一小部分；(ii) 个体规模保持在最小(见第2节)。

SGP-DT 和 DT-EM 的评估节点数几乎完全相同。这表明，用 SGP-DT 的适应度函数和 DT-EM 的适应度函数指导进化，可以获得相同的计算成本，但 SGP-DT 获得了更好的中值 RMSE (平均 5.39%)。DT-NM 总是比 SGP-DT( 0.77 × 平均)评估的节点更少。

Size of the final solutions SGP-DT对个体的最大复杂度没有限制，而 $\epsilon$ -lexicase有 50 个节点的限制，因为在更高的限制下， $\epsilon$ -lexicase 的计算量变得非常昂贵 [9]。SGP-DT 产生的解的规模从 442 到 1，184 个节点(平均 760 )不等，比 $\epsilon$ -lexicase产生的解平均大 15 倍，并且不足以被认为(指数)膨胀。最终解的这种额外复杂度对算法性能有积极贡献。我们正在研究一个后处理阶段来简化最终的解决方案。

DT-EM平均产生 806 个节点的解，DT-NM 平均产生 591 个节点的解。DT-NM 比 DT-EM 产生更小的解，这可能是由于 DT-NM 具有更小的搜索空间( DT-NM 省略了 Min 和 Max 符号)。计算较小的解需要较少的计算量，这解释了为什么 DT-NM 比 SGP-DT 和 DT-EM (见表 3)需要较少的计算量。

Overfitting 图 2 为每个数据集的 SGP-DT 及其两个变体的计算工作量最优 RMSE 的中位数(评估树节点的数量)。遗憾的是，我们使用的 $\epsilon$ -lexicase 的实现并没有在测试中报告中间 RMSE。我们使用 computational effort ，而不是 the number of generations，来公平地比较三种技术。这是因为评估节点的数量在各代之间并不统一。

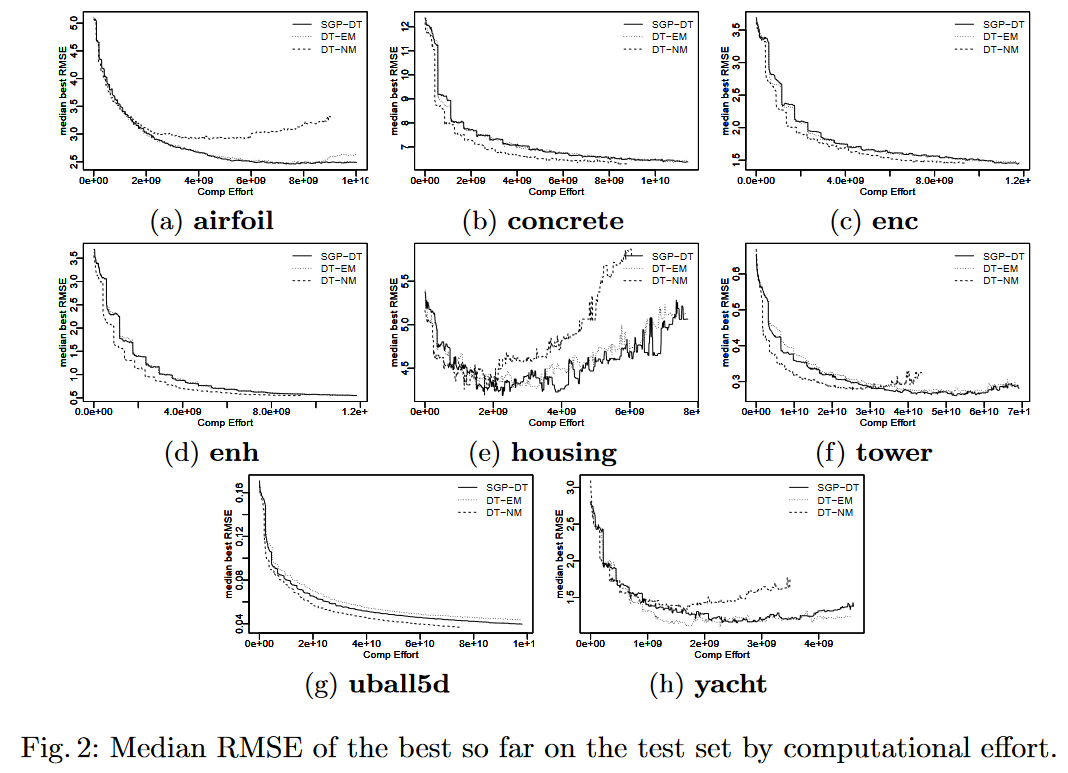
从 8 个图中可以看出，SGP-DT 在数据集 tower 和 yacht 上产生了轻微的过拟合，而在 housing 上产生了严重的过拟合，与 DT-EM 相当，但不如 DT-NM 严重。DT-EM 拟合了四个数据集：airfoil(图 2a )、housing(图 2e )、tower(图 2f )、yacht(图 2h )。性能最差的是 DT-NM，在翼airfoil(图 2a )、housing(图 2e )、tower(图 2f )、yacht(图 2h ) 上表现出严重的过拟合。值得注意的是，这三种技术都适用于数据集 yacht (图2h )和 housing (图 2e)。这可以用它们的实例数(见表 1)相对较低来解释。

对于数据集 Concrete (图 2b)，enc(图 2c)和 enh(图 2d)，三种技术都没有表现出过拟合现象。有趣的是，在这三种情况下，DT-NM 比 SGP-DT 和 DT-EM 具有更低的 RMSE 和更少的计算量。我们猜想，这是因为具体、enc 和 enh 是不需要 Min 和 Max 符号额外表现力的问题。

DT-NM 是产生最小个体的技术，因此我们期望更少的过拟合。令人惊讶的是，事实并非如此。我们认为，为了弥补 Max 和 Min 所引入的不连续性， DT-NM 更频繁地使用了保护分区。这可能导致许多渐进不连续性，已知会增加过拟合 [6]。

单独考虑每个数据集时，SGP-DT 和 DT-EM 大多表现出相似的过拟合，而DT-NM 则表现出更早的过拟合。这表明：(i) 非终端符号 Max 和 Min 有助于缓解过拟合问题；(ii) 依靠适应度函数中的方差 (SGP-DT) 而不是 MSE(DT-EM) 确实有助于降低 RMSE (平均 5.39% ,见表 2)，但不会影响过拟合。

5 Conclusion

本文提出了一种新的动态发现和求解中间动态目标的进化技术 SGP-DT。我们的关键直觉是线性缩放和突变的协同作用有助于在进化过程中交换良好的遗传物质。值得注意的是，SGP-DT 不依赖于任何形式的交叉，因而不存在 [2、7] 的内在局限性。我们的实验结果证实了我们的直觉，表明 SGP-DT 在更低的 RMSE 和更少的计算成本方面都优于 $\epsilon$ -lexicase。这是一个很有前途的结果，因为 $\epsilon$ -lexicase 优于许多受 GP 启发的算法 [29]。

本文激发了未来有趣的工作：

我们不对最终解进行任何类型的后处理以减小其规模。事实上，解中可能包含冗余元素。我们目前正在研究一个后处理步骤，以最小化最终解的大小。

未来一个可能的研究方向是自动识别 SGP-DT 的合适迭代次数。事实上，不同复杂程度和性质的问题可能需要不同的外部和内部迭代次数。

References

Ruberto S, Terragni V, Moore J H. SGP-DT: Semantic genetic programming based on dynamic targets[C]//Genetic Programming: 23rd European Conference, EuroGP 2020, Held as Part of EvoStar 2020, Seville, Spain, April 15–17, 2020, Proceedings. Cham: Springer International Publishing, 2020: 167-183.

算法原理梳理

第一行划分数据集，提取验证集
第二三行取出验证集提取训练集
初始化 target 为最终目标标签
三层 for 循环，第一层 for 训练首先随机初始化种群赋值给 $\mathcal{P}$ 第 7 行, 进入内层循环，第三层 for 遍历 $\mathcal{P}$ 中的每个个体，并利用样本 $\bar{x}$ 与 $\text{target}$ 计算 $\mathcal{I}$ 的线性缩放，即将 $\bar{x}$ 带入 $\mathcal{I}$ 个体，计算得出 $\hat{y}$ , 与 $\text{target}$ 进行线性缩放，计算该个体的 fitness，跳出到第二层 for 循环，通过 fitness 获取 $\mathcal{P}$ 中最好的个体 $\mathcal{I}_{ls}^*$ , 第 13 行计算最好个体的 error，第 14 行，将 $\mathcal{I}_{ls}^*$ 加入到 models 中，紧接着将初始化 $\mathcal{P}^{'}$ 为空，并将 $\mathcal{P}$ 中的精英个体加入到 $\mathcal{P}^{'}$ 中，进入 while 循环， $\mathcal{P}^{'}$ 中的精英个体没有满，则在 $\mathcal{P}$ 中使用锦标赛选择，并对其进行变异后加入到 $\mathcal{P}^{'}$ 中，并用此精英集合 $\mathcal{P}^{'}$ 更新 $\mathcal{P}$ ，继续进行上述操作，从第 8 行开始内层循环，内层循环结束后，此时的 error 将变为下一次的 target，即实现动态目标，第 21 行；第 22 行，在测试集上的效果来进行选择 bestModels，算法 1 的第 23 行通过求和 bestModels 中的所有模型来计算最终模型 finalModel。